Q.No:1 GATE-2012
A particle of mass \(m\) is confined in a two dimensional square well potential of dimension \(a\). This potential \(V(x, y)\) is given by
\[
\left\{
\begin{array}{lll}
V(x, y) & =0 & \text{for }-a<x<a \text{ and }-a<y<a \\
& =\infty & \text{elsewhere}
\end{array}
\right.
\]
The energy of the first excited state for this particle is given by,
(A)
\(\frac{\pi^2 \hbar^2}{ma^2}\)
(B) \(\frac{2\pi^2 \hbar^2}{ma^2}\)
(C) \(\frac{5\pi^2 \hbar^2}{2ma^2}\)
(D) \(\frac{4\pi^2 \hbar^2}{ma^2}\)
Check Answer
Option -Grace
Q.No:2 GATE-2012
The ground state wavefunction for the hydrogen atom is given by \(\psi_{100}=\frac{1}{\sqrt{4\pi}}\left(\frac{1}{a_0}\right)^{3/2}e^{-r/a_0}\), where \(a_0\) is the Bohr radius.
The plot of the radial probability density, \(P(r)\) for the hydrogen atom in the ground state is
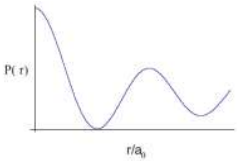
Check Answer
Option D
Q.No:3 GATE-2013
Which one of the following commutation relations is NOT CORRECT? Here, symbols have their usual meanings.
(A) \([L^2, L_z]=0\)
(B) \([L_x, L_y]=i\hbar L_z\)
(C) \([L_z, L_+]=\hbar L_+\)
(D) \([L_z, L_-]=\hbar L_-\)
Check Answer
Option D
Q.No:4 GATE-2013
A proton is confined to a cubic box, whose sides have length \(10^{-12} m\). What is the minimum kinetic energy of the proton? The mass of proton is \(1.67\times 10^{-27} kg\) and Planck's constant is \(6.63\times 10^{-34} Js\).
(A) \(1.1\times 10^{-17} J\)
(B) \(3.3\times 10^{-17} J\)
(C) \(9.9\times 10^{-17} J\)
(D) \(6.6\times 10^{-17} J\)
Check Answer
Option C
Q.No:5 GATE-2013
A spin-half particle is in a linear superposition \(0.8|\uparrow\rangle+0.6|\downarrow\rangle\) of its spin-up and spin-down states. If \(|\uparrow\rangle\) and \(|\downarrow\rangle\) are the eigenstates of \(\sigma_z\) then what is the expectation value, up to one decimal place, of the operator \(10\sigma_z+5\sigma_x\)? Here, symbols have their usual meanings. _________________
Check Answer
Ans 7.6
Q.No:6 GATE-2013
Consider the wave function \(Ae^{ikr}(r_0/r)\), where \(A\) is the normalization constant. For \(r=2r_0\), the magnitude of probability current density up to two decimal places, in units of \((A^2 \hbar k/m)\), is ________.
Check Answer
Ans 0.25
Q.No:7 GATE-2014
An electron in the ground state of the hydrogen atom has the wave function
\[
\Psi(\vec{r})=\frac{1}{\sqrt{\pi a_0^3}} e^{-(r/a_0)}
\]
where \(a_0\) is constant. The expectation value of the operator \(\hat{Q}=z^2-r^2\), where \(z=r\cos{\theta}\) is (Hint: \(\int_{0}^{\infty} e^{-\alpha r} r^n dr=\frac{\Gamma(n)}{a^{n+1}}=\frac{(n-1)!}{a^{n+1}}\))
(A) \(-a_0^2/2\)
(B) \(-a_0^2\)
(C) \(-3a_0^2/2\)
(D) \(-2a_0^2\)
Check Answer
Option D
Q.No:8 GATE-2014
A particle of mass \(m\) is subjected to a potential,
\[
V(x, y)=\frac{1}{2}m\omega^2(x^2+y^2), -\infty\leq x\leq \infty, -\infty\leq y\leq \infty
\]
The state with energy \(4\hbar \omega\) is \(g\)-fold degenerate. The value of \(g\) is ___________.
Check Answer
Ans 3.99-4.01
Q.No:9 GATE-2014
A hydrogen atom is in the state
\[
\Psi=\sqrt{\frac{8}{21}}\psi_{200}-\sqrt{\frac{3}{7}}\psi_{310}+\sqrt{\frac{4}{21}}\psi_{321},
\]
where \(n, l, m\) in \(\psi_{nlm}\) denote the principal, orbital and magnetic quantum numbers, respectively. If \(\vec{L}\) is the angular momentum operator, the average value of \(L^2\) is _________ \(\hbar^2\).
Check Answer
Ans 1.99-2.01
Q.No:10 GATE-2014
If \(L_{+}\) and \(L_{-}\) are the angular momentum ladder operators, then, the expectation value of (\(L_{+}L_{-}+L_{-}L_{+}\)), in the state \(|l=1, m=1\rangle\) of an atom is __________. \(\hbar^2\).
Check Answer
Ans 1.99-2.01
Q.No:11 GATE-2015
Let \(\vec{L}\) and \(\vec{p}\) be the angular and linear momentum operators, respectively, for a particle. The commutator \([L_x, p_y]\) gives
(A) \(-i\hbar p_z\)
(B) \(0\)
(C) \(i\hbar p_x\)
(D) \(i\hbar p_z\)
Check Answer
Option D
Q.No:12 GATE-2015
An operator for a spin-\(1/2\) particle is given by \(\hat{A}=\lambda \vec{\sigma}\cdot \vec{B}\), where \(\vec{B}=\frac{B}{\sqrt{2}}(\hat{x}+\hat{y})\), \(\vec{\sigma}\) denotes Pauli matrices and \(\lambda\) is a constant. The eigenvalues of \(\hat{A}\) are
(A) \(\pm \lambda B/\sqrt{2}\)
(B) \(\pm \lambda B\)
(C) \(0, \lambda B\)
(D) \(0, -\lambda B\)
Check Answer
Option B
Q.No:13 GATE-2016
\(\sigma_x, \sigma_y\) and \(\sigma_z\) are the Pauli matrices. The expression \(2\sigma_x \sigma_y+\sigma_y \sigma_x\) is equal to
(A) \(-3i\sigma_z\)
(B) \(-i\sigma_z\)
(C) \(i\sigma_z\)
(D) \(3i\sigma_z\)
Check Answer
Option C
Q.No:14 GATE-2016
Let \(|l, m\rangle\) be the simultaneous eigenstates of \(L^2\) and \(L_z\). Here \(\vec{L}\) is the angular momentum operator with Cartesian components \((L_x, L_y, L_z)\), \(l\) is the angular momentum quantum number and \(m\) is the azimuthal quantum number. The value of \(\langle 1, 0|(L_x+iL_y)|1, -1\rangle\) is
(A) \(0\)
(B) \(\hbar\)
(C) \(\sqrt{2}\hbar\)
(D) \(\sqrt{3}\hbar\)
Check Answer
Option C
Q.No:15 GATE-2017
The wavefunction of which orbital is spherically symmetric:
(A) \(p_x\)
(B) \(p_y\)
(C) \(s\)
(D) \(d_{xy}\)
Check Answer
Option C
Q.No:16 GATE-2017
For the Hamiltonian \(H=a_0 I+\vec{b}.\vec{\sigma}\) where \(a_0\in R\), \(\vec{b}\) is a real vector, \(I\) is the \(2\times 2\) identity matrix, and \(\vec{\sigma}\) are the Pauli matrices, the ground state energy is
(A) \(|b|\)
(B) \(2a_0-|b|\)
(C) \(a_0-|b|\)
(D) \(a_0\)
Check Answer
Option C
Q.No:17 GATE-2017
The degeneracy of the third energy level of a \(3\)-dimensional isotropic quantum harmonic oscillator is
(A) \(6\)
(B) \(12\)
(C) \(8\)
(D) \(10\)
Check Answer
Option A
Q.No:18 GATE-2018
Which one of the following represents the \(3p\) radial wave function of hydrogen atom? (\(a_0\) is the Bohr radius)
Check Answer
Option B
Q.No:19 GATE-2019
The Hamiltonian for a quantum harmonic oscillator of mass \(m\) in three dimensions is
\[
H=\frac{p^2}{2m}+\frac{1}{2}m\omega^2 r^2
\]
where \(\omega\) is the angular frequency. The expectation value of \(r^2\) in the first excited state of the oscillator in units of \(\frac{\hbar}{m\omega}\) (rounded off to one decimal place) is ______________.
Check Answer
Ans 2.5
Q.No:20 GATE-2019
Electrons with spin in the \(z\)-direction (\(\hat{z}\)) are passed through a Stern-Gerlach (SG) set up with the magnetic field at \(\theta=60^{\circ}\) from \(\hat{z}\). The fraction of electrons that will emerge with their spin parallel to the magnetic field in the SG set up (rounded off to two decimal places) is _________.
\[
\left[
\sigma_x=\begin{pmatrix}0&1\\1&0\end{pmatrix},
\sigma_y=\begin{pmatrix}0&-i\\i&0\end{pmatrix},
\sigma_z=\begin{pmatrix}1&0\\0&-1\end{pmatrix}
\right]
\]
Check Answer
Ans 0.25
Q.No:21 GATE-2020
\(\hat{S}_x\) denotes the spin operator defined as \(\hat{S}_x=\frac{\hbar}{2}\begin{pmatrix}0&1\\1&0\end{pmatrix}\). Which one of the following is correct?
(A) The eigenstates of spin operator \(\hat{S}_x\) are \(|\uparrow\rangle_x\equiv\begin{pmatrix}1\\0\end{pmatrix}\) and \(|\downarrow\rangle_x\equiv\begin{pmatrix}0\\1\end{pmatrix}\)
(B) The eigenstates of spin operator \(\hat{S}_x\) are \(|\uparrow\rangle_x\equiv\frac{1}{\sqrt{2}}\begin{pmatrix}1\\-1\end{pmatrix}\) and \(|\uparrow\rangle_x\equiv\frac{1}{\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix}\)
(C) In the spin state \(\frac{1}{2}\begin{pmatrix}1\\\sqrt{3}\end{pmatrix}\), upon the measurement of \(\hat{S}_x\), the probability for obtaining \(|\uparrow\rangle_x\) is \(\frac{1}{4}\)
(D) In the spin state \(\frac{1}{2}\begin{pmatrix}1\\\sqrt{3}\end{pmatrix}\), upon the measurement of \(\hat{S}_x\), the probability for obtaining \(|\uparrow\rangle_x\) is \(\frac{2+\sqrt{3}}{4}\)
Check Answer
Option D
Q.No:22 GATE-2020
The radial wave function of a particle in a central potential is given by \(R(r)=A\frac{r}{a}\exp{\left(-\frac{r}{2a}\right)}\), where \(A\) is the normalization constant and \(a\) is positive constant of suitable dimensions. If \(\gamma a\) is the most probable distance of the particle from the force center, the value of \(\gamma\) is _______________.
Check Answer
Ans 4
Q.No:23 GATE-2020
A free particle of mass \(M\) is located in a three-dimensional cubic potential well with impenetrable walls. The degeneracy of the fifth excited state of the particle is __________.
Check Answer
Ans 6
Q.No:24 GATE-2020
An electron in a hydrogen atom is in the state \(n=3, l=2, m=-2\). Let \(\hat{L}_y\) denote the \(y\)-component of the orbital angular momentum operator. If \((\Delta \hat{L}_y)^2=\alpha \hbar^2\), the value of \(\alpha\) is _________.
Check Answer
Ans 1
Q.No:25 GATE-2021
Consider a spin \(S=\hbar/2\) particle in the state \(|\phi\rangle=\frac{1}{3}\begin{pmatrix}2+i\\2\end{pmatrix}\). The probability that a measurement finds the state with \(S_x=+\hbar/2\) is
(A) \(5/18\)
(B) \(11/18\)
(C) \(15/18\)
(D) \(17/18\)
Check Answer
Option D
Q.No:26 GATE-2021
The normalized radial wave function of the second excited state of hydrogen atom is
\[
R(r)=\frac{1}{\sqrt{24}}a^{-3/2} \frac{r}{a} e^{-r/2a}
\]
where \(a\) is the Bohr radius and \(r\) is the distance from the center of the atom. The distance at which the electron is most likely to be found is \(y\times a\). The value of \(y\) (in integer) is _____________.
Check Answer
Ans 4
Q.No:27 GATE-2022
From the pairs of operators given below, identify the ones which commute. Here \(l\) and \(j\) correspond to the orbital angular momentum and the total angular momentum, respectively.
(a) \(l^2, j^2\)
(b) \(j^2, j_Z\)
(c) \(j^2, l_Z\)
(d) \(l_Z, j_Z\)
Check Answer
Option a,b,d
Q.No:28 GATE-2022
Pauli spin matrices satisfy
(a) \(\sigma_{\alpha}\sigma_{\beta}-\sigma_{\beta}\sigma_{\alpha}=i\epsilon_{\alpha \beta \gamma} \sigma_{\gamma}\)
(b) \(\sigma_{\alpha}\sigma_{\beta}-\sigma_{\beta}\sigma_{\alpha}=2i\epsilon_{\alpha \beta \gamma} \sigma_{\gamma}\)
(c) \(\sigma_{\alpha}\sigma_{\beta}+\sigma_{\beta}\sigma_{\alpha}=\epsilon_{\alpha \beta \gamma} \sigma_{\gamma}\)
(d) \(\sigma_{\alpha}\sigma_{\beta}+\sigma_{\beta}\sigma_{\alpha}=2\delta_{\alpha \beta}\)
Check Answer
Option b,d
Q.No:29 GATE-2022
In cylindrical coordinates \((s, \varphi, z)\), which of the following is a Hermitian operator?
(a) \(\frac{1}{i} \frac{\partial}{\partial s}\)
(b) \(\frac{1}{i} \left(\frac{\partial}{\partial s}+\frac{1}{s}\right)\)
(c) \(\frac{1}{i} \left(\frac{\partial}{\partial s}+\frac{1}{2s}\right)\)
(d) \(\left(\frac{\partial}{\partial s}+\frac{1}{s}\right)\)
Check Answer
Option c
Q.No:30 GATE-2022
A particle of mass m is moving inside a hollow spherical shell of radius \(r\) so that
the potential is
\[
V(r)=
\left\{
\begin{array}{ll}
0 & \text{for }r<a \\
\infty & \text{for }r\geq a
\end{array}
\right.
\]
The ground state energy and wavefunction of the particle are \(E_0\) and \(R(r)\), respectively. Then which of the following options are correct?
(a) \(E_0=\frac{\hbar^2 \pi^2}{2ma^2}\)
(b) \(-\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)=E_0 R\) (\(r<a\))
(c) \(-\frac{\hbar^2}{2m}\frac{1}{r^2}\frac{d^2 R}{dr^2}=E_0 R\) (\(r<a\))
(d) \(R(r)=\frac{1}{r}\sin{\left(\frac{\pi r}{a}\right)}\) (\(r<a\))
Check Answer
Option a,b,d
Q.No:31 GATE-2023
\(H\) is the Hamiltonian,\(\vec{L}\) the orbital angular momentum and \(L_Z\),
\(z-\)component of \(\vec{L}\). The 1-S state of the hydrogen atom in the non-relativistic formalism is an eigen function of which one of the following sets of operators?
(A) \(H, L^2\) and \(L_Z\)
(B) \(H,\vec{L}, L^2\) and \(L_z\)
(C) \(L^2\) and \(L_Z\) only
(D) \(H\) and \(L_Z\) only
Check Answer
Option A
Q.No:32 GATE-2023
An atom with non-zero magnetic moment has an angular momentum of
magnitude \(\sqrt{12} \hspace{1mm} \hbar\). When a beam of such atoms is passed through a Stern-Gerlach apparatus, how many beams does it split into?
(A) 3
(B) 7
(C) 9
(D) 25
Check Answer
Option B
Q.No:33 GATE-2023
In the vector model of angular momentum applied to atoms, what is the minimum angle in degrees (in integer) made by the orbital angular momentum vector and the positive z axis for a \(2p\) electron?
Check Answer
Ans 45
Q.No:34 GATE-2023
A particle has wavefunction
\[\psi(x,y,z) = N \hspace{0.5mm} z \hspace{0.5mm} e^{-\alpha (x^2+y^2+z^2)},\]
where \(N\) is a normalization constant and \(\alpha\) is a positive constant. In this state, which one of the following options represents the eigenvalues of \(L^2\) and \(L_Z\) respectively?
Some values of \(Y_\ell ^m \) are :
\(Y_0^0= \sqrt{\frac{1}{4\pi}}, Y_1^0= \sqrt{\frac{3}{4\pi}} cos \hspace{0.5mm} \theta, Y_1^{\pm 1}= \sqrt{\frac{3}{8\pi}} sin \hspace{0.5mm} \theta \hspace{0.5mm} e^{\pm i \phi} \)
(A) \(0\) and \(0\)
(B) \(\hbar ^2\) and \(-\hbar\)
(C) \(2\hbar^2\) and \(0\)
(D) \(\hbar^2\) and \(\hbar\)
Check Answer
Option C
Q.No:35 GATE-2023
A spin \(\frac{1}{2}\) particle is in a spin up state along the x-axis (with unit vector \(\hat{x}\)) and is denoted as \(|\frac{1}{2}, \frac{1}{2}\rangle_x\). What is the probability of finding the particle to be in a
spin up state along the direction \(\hat{x}'\), which lies in the xy- plane and makes an angle \(\theta\) with respect to the positive x-axis, if such a measurement is made?
(A) \(\frac{1}{2} cos^2 \frac{\theta}{4}\)
(B) \( cos^2 \frac{\theta}{4}\)
(C) \(\frac{1}{2} cos^2 \frac{\theta}{2}\)
(D) \( cos^2 \frac{\theta}{2}\)
Check Answer
Option D
Q.No: GATE-2023
Consider a particle in a two dimensional infinite square well potential of side \(L\), with \(0 \leq x \leq L\) and \(0 \leq y \leq L\). The wavefunction of the particle is zero only along the line \(y=\frac{L}{2}\), apart from the boundaries of the well. If the energy of the
particle in this state is \(E\), what is the energy of the ground state?
(A) \(\frac{1}{4} E\)
(B) \(\frac{2}{5} E\)
(C) \(\frac{3}{8} E\)
(D) \(\frac{1}{2} E\)
Check Answer
Option B
Q.No:36 GATE-2024
An electron in the Coulomb field of a proton is in the following state of coherent superposition of orthonormal states \( \psi_{nlm} \):
\[
\Psi = \frac{1}{3}\psi_{100} + \frac{1}{\sqrt{3}}\psi_{210} - \frac{\sqrt{5}}{3}\psi_{320}
\]
Let \( E_1, E_2, \) and \( E_3 \) represent the first three energy levels of the system. A sequence of measurements is done on the same system at different times. Energy is measured first at time \( t_1 \) and the outcome is \( E_2 \). Then total angular momentum is measured at time \( t_2 > t_1 \) and finally energy is measured again at \( t_3 > t_2 \). The probability of finding the system in a state with energy \( E_2 \) after the final measurement is \( P/9 \). The value of \( P \) is __________ (in integer).
Check Answer
Ans 9
Q.No:37 GATE-2025
Two projectile protons \(P_{1}\) and \(P_{2}\), both with spin up (along the \(+z\) direction), are scattered from another fixed target proton \(T\) with spin up at rest in the \(xy\) plane, as shown in the figure. They scatter one at a time. The nuclear interaction potential between both the projectiles and the target proton is \(\lambda\,\vec{L}\cdot\vec{S}\), where \(\vec{L}\) is the orbital angular momentum of the system with respect to the target, \(\vec{S}\) is the spin angular momentum of the system, and \(\lambda\) is a negative constant in appropriate units. Which one of the following is correct?
(A) \(P_{1}\) will be scattered in the \(+y\) direction (upward) and \(P_{2}\) will be scattered in the \(-y\) direction (downward)
(B) \(P_{1}\) will be scattered in the \(+y\) direction (upward) and \(P_{2}\) will be scattered in the \(+y\) direction (upward)
(C) \(P_{1}\) will be scattered in the \(-y\) direction (downward) and \(P_{2}\) will be scattered in the \(+y\) direction (upward)
(D) \(P_{1}\) will be scattered in the \(-y\) direction (downward) and \(P_{2}\) will be scattered in the \(-y\) direction (downward)
Check Answer
Option B
Q.No:38 GATE-2025
An electron with mass \(m\) and charge \(q\) is in the spin-up state
\[
\begin{pmatrix}
1 \\
0
\end{pmatrix}
\]
at time \(t = 0\). A constant magnetic field is applied along the \(y\)-axis,
\(B = B_{0}\,\hat{j}\), where \(B_{0}\) is a constant. The Hamiltonian of the system is
\[
H = -\,\hbar \omega \sigma_{y},
\qquad
\omega = \frac{qB_{0}}{2m} > 0,
\qquad
\sigma_{y} =
\begin{pmatrix}
0 & -i \\
i & 0
\end{pmatrix}
\]
The minimum time after which the electron will be in the spin-down state along the \(x\)-axis, i.e.
\[
\frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\
-1
\end{pmatrix},
\]
is
(A) \(\frac{\pi}{8\omega}\)
(B) \(\frac{\pi}{4\omega}\)
(C) \(\frac{\pi}{2\omega}\)
(D) \(\frac{\pi}{\omega}\)
Check Answer
Option B
Q.No:39 GATE-2025
A system of three non-identical spin–\(\frac{1}{2}\) particles has the Hamiltonian
\[
H = \frac{A}{\hbar^{2}}\,
(\vec{S}_{1} + \vec{S}_{2}) \cdot \vec{S}_{3},
\]
where \(\vec{S}_{1}\), \(\vec{S}_{2}\), and \(\vec{S}_{3}\) are the spin operators of particles
labelled 1, 2 and 3 respectively, and \(A\) is a constant with appropriate dimensions.
The set of possible energy eigenvalues of the system is
(A) \(0,\ \frac{A}{2},\ -A\)
(B) \(0,\ \frac{A}{2},\ -\frac{A}{2}\)
(C) \(0,\ \frac{3A}{2},\ -\frac{A}{2}\)
(D) \(0,\ -\frac{3A}{2},\ \frac{A}{2}\)
