Band Theory and Semiconductor Physics CSIR

Q.No:1 CSIR Dec-2014

A junction is made between a metal of work function $W_M$, and a doped semiconductor of work function $W_S$ with $W_M>W_S$. If the electric field at the interface has to be increased by a factor of $3$, then the dopant concentration in the semiconductor would have to be

(1) increased by a factor of $9$

(2) decreased by a factor of $3$

(3) increased by a factor of $3$

(4) decreased by a factor of $\sqrt{3}$

Check Answer

Option 1

Q.No:2 CSIR June-2015

The concentration of electrons, $n$, and holes, $p$, for an intrinsic semiconductor at a temperature $T$ can be expressed as $n = p = AT^{3/2}$ exp$\bigg(-\frac{E_g}{2k_{8}T}\bigg)$, where $E_g$ is the band gap and $A$ is a constant. If the mobility of both types of carriers is proportional to $T^{-3/2}$, then the log of the conductivity is a linear function of $T^{-1}$, with slope

(1) $E_{g}/(2k_{B})$

(2) $E_{g}/k_{B}$

(3) $-E_{g}/(2k_{B})$

(4) $-E_{g}/k_{B}$

Check Answer

Option 3

Q.No:3 CSIR Dec-2015

If the reverse bias voltage of a silicon varactor is increased by a factor of $2$, the corresponding transition capacitance

(1) increases by a factor of $\sqrt{2}$

(2) increases by a factor of $2$

(3) decreases by a factor of $\sqrt{2}$

(4) decreases by a factor of $2$

Check Answer

Option 3

Q.No:4 CSIR Dec-2015

The dispersion relation of electrons in a $3$-dimensional lattice in the tight binding approximation is given by, \[ \varepsilon_k=\alpha \cos{k_x a}+\beta \cos{k_y a}+\gamma \cos{k_z a} \] where $a$ is the lattice constant and $\alpha, \beta, \gamma$ are constants with dimension of energy. The effective mass tensor at the corner of the first Brillouin zone $\left(\frac{\pi}{a}, \frac{\pi}{a}, \frac{\pi}{a}\right)$ is

(1) $\frac{\hbar^2}{a^2}\begin{pmatrix}-\frac{1}{\alpha}&0&0\\0&-\frac{1}{\beta}&0\\0&0&\frac{1}{\gamma}\end{pmatrix}$

(2) $\frac{\hbar^2}{a^2}\begin{pmatrix}-\frac{1}{\alpha}&0&0\\0&-\frac{1}{\beta}&0\\0&0&-\frac{1}{\gamma}\end{pmatrix}$

(3) $\frac{\hbar^2}{a^2}\begin{pmatrix}\frac{1}{\alpha}&0&0\\0&\frac{1}{\beta}&0\\0&0&\frac{1}{\gamma}\end{pmatrix}$

(4) $\frac{\hbar^2}{a^2}\begin{pmatrix}\frac{1}{\alpha}&0&0\\0&\frac{1}{\beta}&0\\0&0&-\frac{1}{\gamma}\end{pmatrix}$

Check Answer

Option 3

Q.No:5 CSIR Dec-2015

For an electron moving through a one-dimensional periodic lattice of periodicity $a$, which of the following corresponds to an energy eigenfunction consistent with Bloch's theorem?

(1) $\psi(x)=A\exp{\left(i\left[\frac{\pi x}{a}+\cos{\left(\frac{\pi x}{2a}\right)}\right]\right)}$

(2) $\psi(x)=A\exp{\left(i\left[\frac{\pi x}{a}+\cos{\left(\frac{2\pi x}{a}\right)}\right]\right)}$

(3) $\psi(x)=A\exp{\left(i\left[\frac{2\pi x}{a}+i\cosh{\left(\frac{2\pi x}{a}\right)}\right]\right)}$

(4) $\psi(x)=A\exp{\left(i\left[\frac{\pi x}{2a}+i\left|\frac{\pi x}{2a}\right|\right]\right)}$

Check Answer

Option 2

Q.No:6 CSIR June-2016

The intensity distribution of a red LED on an absorbing layer of material is a Gaussian centred at the wavelength $\lambda_0=660 nm$ and width $20 nm$. If the absorption coefficient varies with wavelength as $\alpha_0-K(\lambda-\lambda_0)$, where $\alpha_0$ and $K$ are positive constants, the light emerging from the absorber will be

(1) blue shifted retaining the Gaussian intensity distribution

(2) blue shifted with an asymmetric intensity distribution

(3) red shifted retaining the Gaussian intensity distribution

(4) red shifted with an asymmetric intensity distribution

Check Answer

Option 4

Q.No:7 CSIR June-2016

The band energy of an electron in a crystal for a particular $k$-direction has the form $\varepsilon(k)=A-B\cos{2ka}$, where $A$ and $B$ are positive constants and $0< ka< \pi$. The electron has a hole-like behaviour over the following range of $k$:

(1) $\frac{\pi}{4}< ka< \frac{3\pi}{4}$

(2) $\frac{\pi}{2}< ka< \pi$

(3) $0< ka< \frac{\pi}{4}$

(4) $\frac{\pi}{2}< ka< \frac{3\pi}{4}$

Check Answer

Option 1

Q.No:8 CSIR Dec-2016

The active medium in a blue LED (light emitting diode) is a ${Ga_{x}In_{1-x}N}$ alloy. The band gaps of ${Ga N}$ and ${In N}$ are $3.5 eV$ and $1.5 eV$ respectively. If the band gap of ${Ga_{x}In_{1-x}N}$ varies approximately linearly with $x$, the value of $x$ required for the emission of blue light of wavelength $400 nm$ is (take $hc\approx 1200 eV\text{-}nm$)

(1) $0.95$

(2) $0.75$

(3) $0.50$

(4) $0.33$

Check Answer

Option 2

Q.No:9 CSIR Dec-2016

Consider a one-dimensional chain of atoms with lattice constant $a$. The energy of an electron with wave-vector $k$ is $\epsilon(k)=\mu-\gamma \cos{(ka)}$, where $\mu$ and $\gamma$ are constants. If an electric field $E$ is applied in the positive $x$-direction, the time dependent velocity of an electron is (In the following $B$ is the constant)

(1) proportional to $\cos{\left(B-\frac{eE}{\hbar}at\right)}$

(2) proportional to $E$

(3) independent of $E$

(4) proportional to $\sin{\left(B-\frac{eE}{\hbar}at\right)}$

Check Answer

Option 1 OR 4

Q.No:10 CSIR Dec-2016

A thin rectangular conducting plate of length $a$ and width $b$ is placed in the $xy$-plane in two different orientations, as shown in the figures below. In both cases a magnetic field $B$ is applied in the $z$-direction and a current flows in the $x$ direction due to the applied voltage $V$.

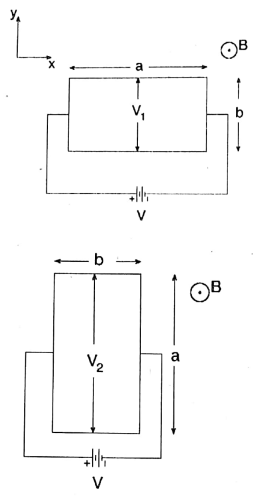
If the Hall voltage across the $y$-direction in the two cases satisfy $V_2=2V_1$, the ratio $a:b$ must be

(1) $1:2$

(2) $1:\sqrt{2}$

(3) $2:1$

(4) $\sqrt{2}:1$

Check Answer

Option 4

Q.No:11 CSIR June-2017

The energy gap and lattice constant of an indirect band gap semiconductor are $1.875 eV 0.52 nm$, respectively. For simplicity take the dielectric constant of the material to be unity. When it is excited by broadband radiation, an electron initially in the valence band at $k=0$ makes a transition to the conduction band. The wavevector of the electron in the conduction band, in terms of the wavevector $k_{\text{max}}$ at the edge of the Brillouin zone, after the transition is closest to

(1) $k_{\text{max}}/10$

(2) $k_{\text{max}}/100$

(3) $k_{\text{max}}/1000$

(4) $0$

Check Answer

Option 3

Q.No:12 CSIR June-2017

The electrical conductivity of copper is approximately $95\%$ of the electrical conductivity of silver, while the electron density in silver is approximately $70\%$ of the electron density in copper. In Drude's model, the approximate ratio $\tau_{{Cu}}/\tau_{{Ag}}$ of the mean collision time in copper ($\tau_{{Cu}}$) to the mean collision time in silver ($\tau_{{Ag}}$) is

(1) $0.44$

(2) $1.50$

(3) $0.33$

(4) $0.66$

Check Answer

Option 4

Q.No:13 CSIR Dec-2017

Consider a two-dimensional material of length $\ell$ and width $w$ subjected to a constant magnetic field $B$ applied perpendicular to it. The number of charge carriers per unit area may be expressed as $n=k|q|B/(2\pi \hbar)$, where $k$ is a positive real number and $q$ is the carrier charge. Then the Hall resistivity $\rho_{xy}$ is

(1) $\frac{2\pi \hbar k}{q^2} \sqrt{\frac{\ell}{w}}$

(2) $\frac{2\pi \hbar}{kq^2} \sqrt{\frac{w}{\ell}}$

(3) $\frac{2\pi \hbar}{kq^2}$

(4) $\frac{2\pi \hbar k}{q^2}$

Check Answer

Option 3

Q.No:14 CSIR June-2018

The dispersion relation for the electrons in the conduction band of a semiconductor is given by $E=E_0+\alpha k^2$, where $\alpha$ and $E_0$ are constants. If $\omega_C$ is the cyclotron resonance frequency of the conduction band electrons in a magnetic field $B$, the value of $\alpha$ is

(1) $\frac{\hbar^2 \omega_C}{4eB}$

(2) $\frac{2\hbar^2 \omega_C}{eB}$

(3) $\frac{\hbar^2 \omega_C}{eB}$

(4) $\frac{\hbar^2 \omega_C}{2eB}$

Check Answer

Option 4

Q.No:15 CSIR Dec-2018

A silicon crystal is doped with phosphorus atoms. (The binding energy of a ${H}$ atom is $13.6 eV$, the dielectric constant of silicon is $12$ and the effective mass of electrons in the crystal is $0.4m_e$.) The gap between the donor energy level and the bottom of the conduction band is nearest to

(1) $0.01 eV$

(2) $0.08 eV$

(3) $0.02 eV$

(4) $0.04 eV$

Check Answer

Option 4

Q.No:16 CSIR June-2019

A bound electron and hole pair interacting via Coulomb interaction in a semiconductor is called an exciton. The effective masses of an electron and a hole are about $0.1m_e$ and $0.5m_e$ respectively, where $m_e$ is the rest mass of the electron. The dielectric constant of the semiconductor is $10$. Assuming that the energy levels of the excitons are hydrogen-like, the binding energy of an exciton (in units of the Rydberg constant) is closest to

(1) $2\times 10^{-3}$

(2) $2\times 10^{-4}$

(3) $8\times 10^{-4}$

(4) $3\times 10^{-3}$

Check Answer

Option 3

Q.No:17 CSIR June-2019

Consider an array of atoms in one dimension with an ensemble averaged periodic density distribution as shown in the figure.

If $k$ is the wave number and $S(k, \Delta)$ denotes the Fourier transform of the density-density correlation function, the ratio $S(k, \Delta)/S(k, 0)$ is

(1) $\cos{\left(\frac{k\Delta}{2}\right)}$

(2) $\cos^2{\left(\frac{k\Delta}{2}\right)}$

(3) $\frac{2}{k\Delta}\sin{\left(\frac{k\Delta}{2}\right)}$

(4) $\frac{4}{k^2 \Delta^2}\sin^2{\left(\frac{k\Delta}{2}\right)}$

Check Answer

Option 4

Q.No:18 CSIR Dec-2019

For a crystal, let $\phi$ denote the energy required to create a pair of vacancy and interstitial defects. If $n$ pairs of such defects are formed, and $n\ll N, N'$, where $N$ and $N'$ are, respectively, the total number of lattice and interstitial sites, then $n$ is approximately

(1) $\sqrt{NN'} e^{-\phi/(2k_B T)}$

(2) $\sqrt{NN'} e^{-\phi/(k_B T)}$

(3) $\frac{1}{2}(N+N') e^{-\phi/(2k_B T)}$

(4) $\frac{1}{2}(N+N') e^{-\phi/(k_B T)}$

Check Answer

Option 1

Q.No:19 CSIR Dec-2019

The Hall coefficient for a semiconductor having both types of carriers is given as \[ R_H=\frac{p\mu_p^2-n\mu_n^2}{|e|(p\mu_p+n\mu_n)^2} \] where $p$ and $n$ are the carrier densities of the holes and electrons, $\mu_p$ and $\mu_n$ are their respective mobilities. For a $p$-type semiconductor in which the mobility of holes is less than that of electrons, which of the following graphs best describes the variation of the Hall coefficient with temperature?

Check Answer

Option 4

Q.No:20 CSIR Assam Dec-2019

A $pn$-junction diode has a linearly graded doping profile given by $N_D-N_A=ax$, where $a>0$ is constant, $N_D$ is the donor density and $N_A$ is the acceptor density, with the $x$-axis along the sample with the origin at its centre, as shown in the figure.

The figure that best represents the charge density profile in the depletion region along the $x$-direction, is

Check Answer

Option 4

Q.No:21 CSIR June-2020

A certain two-dimensional solid crystallises to a square monoatomic lattice with lattice constant $a$. Each atom can contribute an integer number of free conduction electrons. The minimum number of electrons each atom must contribute such that the free electron Fermi circle at zero temperature encloses the first Brillouin zone completely, is

(1) $3$

(2) $1$

(3) $4$

(4) $2$

Check Answer

Option 3

Q.No:22 CSIR June-2020

A tight binding model of electrons in one dimension has the dispersion relation $\varepsilon(k)=-2t(1-\cos{ka})$, where $t>0, a$ is the lattice constant and $-\frac{\pi}{a}<k<\frac{\pi}{a}$. Which of the following figures best represents the density of states over the range $\frac{\pi}{2a}\leq k<\frac{\pi}{a}$?

Check Answer

Option 2

Q.No:23 CSIR June-2020

The temperature variation of the resistivity of four materials are shown in the following graphs.

The material that would make the most sensitive temperature sensor, when used at temperatures between $T_1$ and $T_2$, is

(4) A

(4) B

(4) C

(4) D

Check Answer

Option 3

Q.No:24 CSIR June-2023

The Hall coefficient $R_H$ of a sample can be determined from the measured Hall voltage $V_H=\frac{1}{d}R_HBI+RI$, where $d$ is the thickness of the sample, $B$ is the applied magnetic field, $I$ is the current passing through the sample and $R$ is an unwanted offset resistance. A lock-in detection technique is used by keeping $I$ constant with the applied magnetic field being modulated as $B=B_0sin\Omega t$, where $B_0$ is the amplitude of the magnetic field and $\Omega$ is frequency of the reference signal. The measured $V_H$ is

1)$B_0(\frac{R_HI}{d})$

2) $\frac{B_0}{\sqrt{2}}(\frac{R_HI}{d})$

3) $\frac{I}{\sqrt{2}}(\frac{R_HB_0}{d}+R)$

4) $I(\frac{R_HB_0}{d}+R)$

Check Answer

Option 2

Q.No:25 CSIR Dec-2023

The lattice constant of the bcc structure of sodium metal is 4.22 A. Assuming the mass of the electron inside the metal to be the same as free electron mass, the free electron Fermi energy is closest to

1) $3.2 \hspace{3mm}eV$

2) $2.9 \hspace{3mm}eV$

3) $3.5 \hspace{3mm}eV$

4) $2.5\hspace{3mm} eV$

Check Answer

Option 1

Q.No:26 CSIR Dec-2023

The collision time of the electrons in a metal in the Drude model is $ \tau $ and their plasma frequency is $ \omega_p $. If this metal is placed between the plates of a capacitor, the time constant associated with the decay of the electric field inside the metal is

1) $ \tau + \frac{1}{\omega_p} $

2) $ \omega_p \tau^2 $

3) $ \frac{1}{\omega_p^2 \tau} $

4) $ \frac{\tau}{1 + \omega_p \tau} $

Check Answer

Option 3

Q.No:27 CSIR Dec-2023

The light incident on a solar cell has a uniform photon flux in the energy range of $ 1 \text{ eV} $ to $ 2 \text{ eV} $ and is zero elsewhere. The active layer of the cell has a bandgap of $ 1.5 \text{ eV} $ and absorbs $ 80\% $ of the photons with energies above the bandgap. Ignoring non-radiative losses, the power conversion efficiency (ratio of the output power to the input power) is closest to

1) 47 %

2) 70 %

3) 23 %

4) 35 %

Check Answer

Option 1

Q.No:29 CSIR June-2024

The band dispersion of electrons in a two-dimensional square lattice (lattice constant $ a $) is given by, \[ E(k_x, k_y) = -2(t_x \cos k_x a + t_y \cos k_y a), \] where $ t_x, t_y > 0 $. The effective mass tensor $ m^* = \begin{pmatrix} m_{xx} & m_{xy} \\ m_{yx} & m_{yy} \end{pmatrix} $ of electrons at $\vec{k} = \begin{pmatrix} \frac{\pi}{a}, \frac{\pi}{a} \end{pmatrix} $ is:

1) $ \begin{pmatrix} 0 & \frac{\hbar^2}{2a^2 t_x t_y} \\ \frac{\hbar^2}{2a^2 t_x t_y} & 0 \end{pmatrix} $

2) $ \begin{pmatrix} \frac{\hbar^2}{2a^2 t_x} & 0 \\ 0 & \frac{\hbar^2}{2a^2 t_y} \end{pmatrix} $

3) $ \begin{pmatrix} -\frac{\hbar^2}{2a^2 t_x} & 0 \\ 0 & -\frac{\hbar^2}{2a^2 t_y} \end{pmatrix} $

4) $ \begin{pmatrix} 0 & -\frac{\hbar^2}{2a^2 (t_x + t_y)} \\ -\frac{\hbar^2}{2a^2 (t_x + t_y)} & 0 \end{pmatrix} $

Check Answer

Option 3

Q.No:28 CSIR Dec-2024

Consider $N$ mutually non-interacting electrons moving in a crystal where the ionic potential seen by an electron satisfies the condition \[ V(\vec r) = V(\vec r + \vec R), \] where $\vec R$ is one of the lattice translation vectors. The energy eigenstates of the electrons are labelled by $\psi_{\vec k}(\vec r)$, where $\vec k$ is a vector in the first Brillouin zone. Which of the following is true?

1) $|\psi_{\vec k}(\vec r)|$ is constant.

2) $\psi_{\vec k}(\vec r)$ is also an eigenstate of the momentum operator.

3) $\psi_{\vec k}(\vec r) = \psi_{\vec k}(\vec r + \vec R)$

4)$|\psi_{\vec k}(\vec r)| = |\psi_{\vec k}(\vec r + \vec R)|$

Check Answer

Option 4

Q.No:30 CSIR June-2025

A semiconductor has the dispersion relation \[ E = E_0 - A \cos(a k_x), \] where $A$ and $a$ are positive constants. The effective electron mass close to the minimum energy is

1) $\frac{\hbar^2}{A^2 a}$

2) $\frac{1}{4}\,\frac{\hbar^2}{A^2 a}$

3) $\frac{\hbar^2}{A a^2}$

4) $\frac{1}{2}\,\frac{\hbar^2}{A a^2}$