Q.No:1 GATE-2012
A particle is constrained to move in a truncated harmonic potential well (\(x>0\)) as shown in the figure. Which one of the following statements is CORRECT?
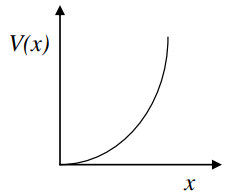
(A) The parity of the first excited state is even
(B) The parity of the ground state is even
(C) The ground state energy is \(\frac{1}{2}\hbar \omega\)
(D) The first excited state energy is \(\frac{7}{2}\hbar \omega\)
Check Answer
Option D
Q.No:2 GATE-2014
The recoil momentum of an atom is \(p_A\) when it emits an infrared photon of wavelength \(1500 nm\), and it is \(p_B\) when it emits a photon of visible wavelength \(500 nm\). The ratio \(\frac{p_A}{p_B}\) is
(A) \(1:1\)
(B) \(1:\sqrt{3}\)
(C) \(1:3\)
(D) \(3:2\)
Check Answer
Option C
Q.No:3 GATE-2014
A one dimensional harmonic oscillator is in the superposition of number states, \(|n\rangle\), given by
\[
|\psi\rangle=\frac{1}{2}|2\rangle+\frac{\sqrt{3}}{2}|3\rangle.
\]
The average energy of the oscillator in the given state is ______ \(\hbar \omega\).
Check Answer
ANS 3.2-3.3
Q.No:4 GATE-2015
Suppose a linear harmonic oscillator of frequency \(\omega\) and mass \(m\) is in the state \(|\psi\rangle=\frac{1}{\sqrt{2}}\left[|\psi_0\rangle+e^{i\frac{\pi}{2}}|\psi_1\rangle\right]\) at \(t=0\) where \(|\psi_0\rangle\) and \(|\psi_1\rangle\) are the ground and the first excited states, respectively. The value of \(\langle \psi|x|\psi\rangle\) in the units of \(\sqrt{\frac{\hbar}{m\omega}}\) at \(t=0\) is ______
Check Answer
ANS 0
Q.No:5 GATE-2016
The total power emitted by a spherical black body of radius \(R\) at a temperature \(T\) is \(P_1\). Let \(P_2\) be the total power emitted by another spherical black body of radius \(R/2\) kept at temperature \(2T\). The ratio, \(P_1/P_2\) is ______. (Give your answer upto two decimal places)
Check Answer
ANS 0.25
Q.No:6 GATE-2016
The state of a system is given by
\[
|\psi\rangle=|\phi_1\rangle+2|\phi_2\rangle+3|\phi_3\rangle
\]
where \(|\phi_1\rangle, |\phi_2\rangle\) and \(|\phi_3\rangle\) form an orthonormal set. The probability of finding the system in the state \(|\phi_2\rangle\) is ______. (Give your answer upto two decimal places)
Check Answer
ANS 0.27-0.29
Q.No:7 GATE-2017
The Compton wavelength of a proton is ______ fm. (up to two decimal places). \(m_p\)=\(1.67\times 10^{-27}\) kg, h=\(6.626\times 10^{-34}\) Js, e=\(1.602\times 10^{-19}\) C, c=\(3\times 10^8 ms^{-1}\)
Check Answer
ANS 1.30-1.34
Q.No:8 GATE-2017
Consider a one-dimensional potential well of width \(3 nm\). Using the uncertainty principle \(\left(\Delta x.\Delta p\geq \hbar/2\right)\), an estimate of the minimum depth of the well such that it has at least one bound state for an electron is (\(m_{e}=9.31\times 10^{-31} kg, h=6.626\times10^{-34} Js, e=1.602\times10^{-19} C\)):
(A) \(1 {\mu eV}\)
(B) \(1 {meV}\)
(C) \(1 {eV}\)
(D) \(1 {MeV}\)
Check Answer
Option B
Q.No:9 GATE-2017
The integral \(\int_{0}^{\infty} x^2 e^{-x^2} dx\) is equal to __________. (up to two decimal places).
Check Answer
ANS 0.43-0.45
Q.No:10 GATE-2018
Given the following table,
which one of the following correctly matches the experiments from Group I to their inferences in Group II?
(A) P-2, Q-3, R-4, S-1
(B) P-3, Q-4, R-2, S-1
(C) P-1, Q-3, R-2, S-4
(D) P-2, Q-1, R-4, S-3
Check Answer
Option B
Q.No:11 GATE-2018
A two-state quantum system has energy eigenvalues \(\pm \epsilon\) corresponding to the normalized states \(|\psi_{\pm}\). At time \(t=0\), the system is in quantum state \(\frac{1}{\sqrt{2}}[|\psi_+\rangle+|\psi_-\rangle]\). The probability that the system will be in the same state at \(t=h/(6\epsilon)\) is ____________ (up to two decimal places).
Check Answer
ANS 0.25
Q.No:12 GATE-2018
Two solid spheres A and B have same emissivity. The radius of A is four times the radius of B, and temperature of A is twice the temperature of B. The ratio of the rate of heat radiated from A to that from B is ______________.
Check Answer
ANS 256
Q.No:13 GATE-2019
The wave function \(\psi(x)\) of a particle is as shown below
Here \(K\) is a constant, and \(a>d\). The position uncertainty \(\langle \Delta x\rangle\) of the particle is
(A) \(\sqrt{\frac{a^2+3d^2}{12}}\)
(B) \(\sqrt{\frac{3a^2+d^2}{12}}\)
(C) \(\sqrt{\frac{d^2}{6}}\)
(D) \(\sqrt{\frac{d^2}{24}}\)
Check Answer
Option B
Q.No:14 GATE-2019
Consider the motion of a particle along the \(x\)-axis in a potential \(V(x)=F|x|\). Its ground state energy \(E_0\) is estimated using the uncertainty principle. Then \(E_0\) is proportional to
(A) \(F^{\frac{1}{3}}\)
(B) \(F^{\frac{1}{2}}\)
(C) \(F^{\frac{2}{5}}\)
(D) \(F^{\frac{2}{3}}\)
Check Answer
Option D
Q.No:15 GATE-2020
A quantum particle is subjected to the potential
\[
V(x)=
\left\{
\begin{array}{ll}
\infty, & x\leq -\frac{a}{2} \\
0, & -\frac{a}{2}<x<\frac{a}{2} \\
\infty, & x\geq \frac{a}{2}.
\end{array}
\right.
\]
The ground state wave function of the particle is proportional to
(A) \(\sin{\left(\frac{\pi x}{2a}\right)}\)
(B) \(\sin{\left(\frac{\pi x}{a}\right)}\)
(C) \(\cos{\left(\frac{\pi x}{2a}\right)}\)
(D) \(\cos{\left(\frac{\pi x}{a}\right)}\)
Check Answer
Option D
Q.No:16 GATE-2020
Let \(\hat{a}\) and \(\hat{a}^{\dagger}\), respectively denote the lowering and raising operators of a one-dimensional simple harmonic oscillator. Let \(|n\rangle\) be the energy eigenstate of the simple harmonic oscillator. Given that \(|n\rangle\) is also an eigenstate of \(\hat{a}^{\dagger}\hat{a}^{\dagger}\hat{a}\hat{a}\), the corresponding eigenvalue is
(A) \(n(n-1)\)
(B) \(n(n+1)\)
(C) \((n+1)^2\)
(D) \(n^2\)
Check Answer
Option A
Q.No:17 GATE-2021
A light source having its intensity peak at the wavelength \(289.8 nm\) is calibrated as 10000
K which is the temperature of an equivalent black body radiation. Considering the same calibration, the temperature of light source (in K) having its intensity peak at the wavelength \(579.6 nm\) (rounded off to the nearest integer) is _____________.
Check Answer
ANS 5000
Q.No:18 GATE-2021
Consider a state described by \(\psi(x, t)=\psi_2(x, t)+\psi_4(x, t)\), where \(\psi_2(x, t)\) and \(\psi_4(x, t)\) are respectively the second and fourth normalized harmonic oscillator wave functions and \(\omega\) is the angular frequency of the harmonic oscillator. The wave function \(\psi(x, t=0)\) will be orthogonal to \(\psi(x, t)\) at time \(t\) equal to
(A) \(\frac{\pi}{2\omega}\)
(B) \(\frac{\pi}{\omega}\)
(C) \(\frac{\pi}{4\omega}\)
(D) \(\frac{\pi}{6\omega}\)
Check Answer
Option A
Q.No:19 GATE-2022
The wavefunction of a particle in a one-dimensional infinite well of size \(2a\) at a certain time is
\[\psi(x)=\frac{1}{\sqrt{6a}}\left[\sqrt{2}\sin{\left(\frac{\pi x}{a}\right)}\right]\]
\[ +\frac{1}{\sqrt{6a}} \left[\sqrt{3}\cos{\left(\frac{\pi x}{2a}\right)+\cos{\left(\frac{3\pi x}{2a}\right)}}\right] \]
Probability of finding the particle in \(n=2\) state at that time is ------------------- \(\%\) (Round off to the nearest integer)
Check Answer
ANS 33-34
Q.No:20 GATE-2023
Which one of the following options is the most appropriate match between the items given in Column 1 and Column 2 ?
(A) (i) - T; (ii) - P,S,T; (iii) - Q,R; (iv) - S
(B) (i) - P,T; (ii) - S; (iii) - R,S; (iv) - S,T
(C) (i) - T; (ii) - R,S; (iii) - Q,R; (iv) - S
(D) (i) - S,T; (ii) - P,S; (iii) - R,T; (iv) - S
Check Answer
Option A
Q.No:22 GATE-2024
The wavefunction of a particle in an infinite one-dimensional potential well at time \( t \) is
\[\psi(x, t) = \sqrt{\frac{2}{3}} e^{-iE_1t/\hbar} \psi_1(x) + \frac{1}{\sqrt{6}} e^{i\pi/6} e^{-iE_2t/\hbar} \psi_2(x) +\]
\[\frac{1}{\sqrt{6}} \times e^{i\pi/4} e^{-iE_3t/\hbar} \psi_3(x)\]
where \( \psi_1, \psi_2 \) and \( \psi_3 \) are the normalized ground state, the normalized first excited state and the normalized second excited state, respectively. \( E_1, E_2 \) and \( E_3 \) are the eigen-energies corresponding to \( \psi_1, \psi_2 \) and \( \psi_3 \), respectively. The expectation value of energy of the particle in state \( \psi(x, t) \) is
1) \(\frac{17}{6} E_1\)
2)\(\frac{2}{3} E_1\)
3 \(\frac{3}{2} E_1\)
4)\(14 E_1\)
Check Answer
Option 1
Q.No:23 GATE-2024
A particle of mass \(m\) is moving in the potential
\[ V(x) =
\begin{cases}
V_0 + \frac{1}{2}m\omega_0^2x^2, & x > 0, \\
\infty, & x \leq 0,
\end{cases}
\]
Figures P, Q, R and S show different combinations of the values of \(\omega_0\) and \(V_0\).
\(E_j^{(P)}\), \(E_j^{(Q)}\), \(E_j^{(R)}\) and \(E_j^{(S)}\) with \(j = 0,1,2,...\) are the eigen-energies of the j-th level for the potentials shown in figures P, Q, R and S, respectively. Which of the statement is/are true?
1)\(E_0^{(P)} = E_0^{(Q)}\)
2) \(E_0^{(Q)} = E_0^{(S)}\)
3) \(E_0^{(P)} = E_1^{(R)}\)
4)\(E_0^{(R)} \neq E_0^{(Q)}\)
Check Answer
Option 2,3,4
Q.No:24 GATE-2024
The wavefunction for a particle is given by the form \( e^{-(i\alpha x + \beta)} \), where \( \alpha \) and \( \beta \) are real constants. In which one of the following potentials \( V(x) \), the particle is moving?
1) \( V(x) \propto \alpha^2 x^2 \)
2) \( V(x) \propto e^{-\alpha x} \)
3) \( V(x) = 0 \)
4) \( V(x) \propto \sin(\alpha x) \)
Check Answer
Option 3
Q.No:25 GATE-2025
A particle of mass \(m\) is in a potential \(V(x) = \frac{1}{2} m \omega^{2} x^{2}\) for \(x > 0\) and \(V(x) = \infty\) for \(x \le 0\), where \(\omega\) is the angular frequency. The ratio of the energies corresponding to the lowest energy level to the next higher level is
1) \(\frac{3}{7}\)
2) \(\frac{1}{2}\)
3) \(\frac{1}{3}\)
4) \(\frac{3}{5}\)
Check Answer
Option 1
Q.No:26 GATE-2025
Which of the following option(s) is/are correct for photons?
1) Its rest mass is zero, but its energy is non-zero
2) It carries non-zero linear momentum
3) It carries zero spin angular momentum
4) It has two linearly independent states of polarization
Check Answer
Option 1,2,4
Q.No:27 GATE-2025
Let \(|m\rangle\) and \(|n\rangle\) denote the energy eigenstates of a one-dimensional simple harmonic oscillator. The position and momentum operators are \(\hat{X}\) and \(\hat{P}\), respectively. The matrix element \(\langle m|\,\hat{P}\hat{X}\,|n\rangle\) is non-zero when
1) \(m = n \pm 2\) only
2) \(m = n\) or \(m = n \pm 2\)
3) \(m = n \pm 3\) only
4) \(m = n \pm 1\) only
