Part-C Solutions
Quantum Mechanics
Q.N.1
A quantum particle of mass \( m \) is moving in a one dimensional potential
\[ V(x) = V_0 \theta(x) – \lambda \delta(x), \]
where \( V_0 \) and \( \lambda \) are positive constants, \( \theta(x) \) is the Heaviside step function and \( \delta(x) \) is the Dirac delta function. The leading contribution to the reflection coefficient for the particle incident from the left with energy \( E \gg V_0 > \lambda \) and \( \sqrt{2mE} \gg \frac{V_0 \hbar}{\lambda} \) is
- \( \frac{V_0^2}{4E^2} \)
- \( \frac{V_0^2}{8E^2} \)
- \( \frac{m \lambda^2}{2E \hbar^2} \)
- \( \frac{m \lambda^2}{4E \hbar^2} \)
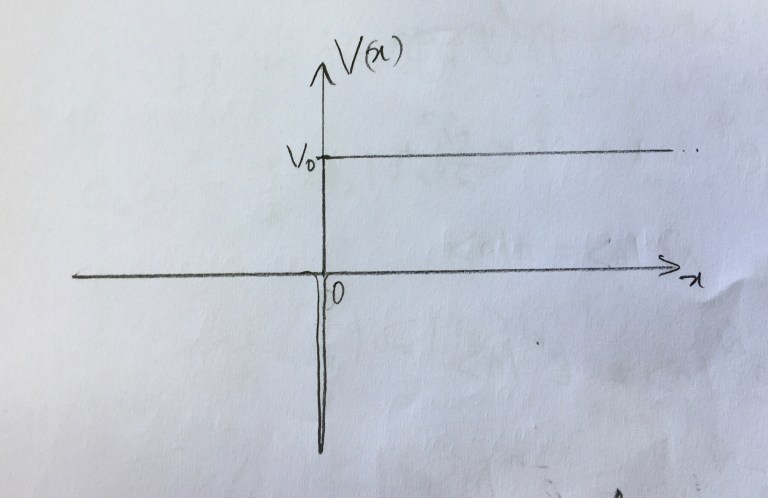
Solution :
Reflection coefficient for Dirac Well
\[
R_d = \frac{1}{1 + \left(2\hbar^2 E / m \lambda^2\right)}
\]
Reflection coefficient for Step Potential
\[
R_s = \left( \frac{\sqrt{E} – \sqrt{E – V_0}}{\sqrt{E} + \sqrt{E + V_0}} \right)^2
\]
As \( E \gg V_0 \), \( E \pm V_0 \approx E \), \( R_s \approx 0 \)
As \( E \gg \lambda \), \( 1 + \left(2\hbar^2E/m \lambda^2\right) \approx \frac{2\hbar^2E}{m \lambda^2} \)
\[
R = R_d \approx \frac{1}{\left(2\hbar^2E/m \lambda^2\right)} = \frac{m \lambda^2}{2\hbar^2E}
\]
Q.N.2
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Atomic Physics
Q.N.1
The ionization potential of hydrogen atom is 13.6 eV, and \(\lambda_H\) and \(\lambda_D\) denote longest wavelengths in Balmer spectrum of hydrogen and deuterium atoms, respectively. Ignoring the fine and hyperfine structures, the percentage difference \(y = \frac{\lambda_H – \lambda_D}{\lambda_H} \times 100\), is closest to
- \(1.0003\%\)
- \(-0.03\%\)
- \(0.03\%\)
- \(-1.0003\%\)
Solution:
\( \frac{1}{\lambda} \propto R \), (\(R\) is Rydberg constant)
\( R \propto \mu \), (\(\mu\) is reduced mass of nucleus and electron system.)
\[
\frac{\lambda_D}{\lambda_H} = \frac{\mu_H}{\mu_D} = \frac{\left( \frac{m_e m_p}{m_e + m_p} \right)}{\left( \frac{m_e 2m_p}{m_e + 2m_p} \right)}
\]
\[
\frac{\lambda_D}{\lambda_H} = 0.99972
\]
\[
1 – \frac{\lambda_D}{\lambda_H} = 2.72 \times 10^{-4}
\]
\[
\left( \frac{\lambda_H – \lambda_D}{\lambda_H} \right) \times 100 \approx 0.03
\]
Q.N.2
A solar probe mission detects a fractional wavelength shift \((\Delta \lambda / \lambda)\) of the spectral line \(\lambda = 630\ nm\) within a sunspot to be of the order of \(10^{-5}\). Assuming this shift is caused by the normal Zeeman effect (i.e., neglecting other physical effects), the estimated magnetic field (in tesla) within the observed sunspot is closest to
- \(3 \times 10^{-5}\)
- \(300\)
- \(0.3\)
- \(3 \times 10^{5}\)
Solution :
\[
E = \frac{hc}{\lambda}
\]
\[
\Delta E = \frac{hc \Delta \lambda}{\lambda^2}, \quad \Delta E = \mu_B B
\]
\[
\mu_B B = hc \left( \frac{\Delta \lambda}{\lambda} \right) \frac{1}{\lambda}
\]
\[
B = \frac{hc}{\mu_B} \left( \frac{\Delta \lambda}{\lambda} \right) \frac{1}{\lambda}
\]
Part-B Solutions
Quantum Mechanics
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.