Q.No:1 JAM-2015
For an electromagnetic wave traveling in free space, the electric field is given by \(\vec{E}=100 \hspace{1mm} cos (10^8t +kx)\hat{j}\) V/m. Which of the following statements are true?
(A)
The wavelength of the wave in meter is \(6\pi\)
(B)
The corresponding magnetic field is directed along the positive z direction
(C)
The Poynting vector is directed along the positive z direction
(D)
The wave is linearly polarized
Check Answer
Option A,D
Q.No:2 JAM-2015
The power radiated by sun is \(3.8\times 10^{26}\)W and its radius is \(7\times 10^5\)km. The magnitude of the
Poynting vector (in \(W/cm^2\)) at the surface of the sun is _______________.
Check Answer
Ans 6165-6180
Q.No:3 JAM-2015
In a region of space, a time dependent magnetic field \(B(t)=0.4\)t Tesla points vertically upwards. Consider a horizontal, circular loop of radius 2 cm in this region. The magnitude of the electric field (in mV/m) induced in the loop is __________________.
Check Answer
Ans 4
Q.No:4 JAM-2015
A plane electromagnetic wave of frequency \(5\times 10^{14}\)Hz and amplitude \(10^3\) V/m, traveling in a homogeneous dielectric medium of dielectric constant 1.69, is incident normally at the interface with a second dielectric medium of dielectric constant 2.25. The ratio of the amplitude of the transmitted wave to that of the incident wave is _____________.
Check Answer
Ans 0.80-0.97
Q.No:5 JAM-2016
Consider a small bar magnet undergoing simple harmonic motion (SHM) along the x-axis. A coil whose plane is perpendicular to the x-axis is placed such that the magnet passes in and out of it
during its motion. Which one of the following statements is correct? Neglect damping effects.
(A)
Induced e.m.f. is minimum when the center of the bar magnet crosses the coil.
(B)
The frequency of the induced current in the coil is half of the frequency of the SHM.
(C)
Induced e.m.f. in the coil will not change with the velocity of the magnet.
(D)
The sign of the e.m.f. depends on the pole (N or S) face of the magnet which enters into the
coil.
Check Answer
Option A
Q.No:6 JAM-2016
A 1 W point source at origin emits light uniformly in all the directions. If the units for both the axes are measured in centimetre, then the Poynting vector at the point (1,1,0) in W/\(cm^2\) is
(A)
\(\frac{1}{8\pi \sqrt{2}}(\hat{e}_x+\hat{e}_y)\)
(B)
\(\frac{1}{16\pi}(\hat{e}_x+\hat{e}_y)\)
(C)
\(\frac{1}{16\pi \sqrt{2}}(\hat{e}_x+\hat{e}_y)\)
(D)
\(\frac{1}{4\pi \sqrt{2}}(\hat{e}_x+\hat{e}_y)\)
Check Answer
Option A
Q.No:7 JAM-2017
The dispersion relation for electromagnetic waves travelling in a plasma is given as \(\omega^2=c^2k^2+\omega_p^2\) where \(c\) and \(\omega_p\) are constants. In this plasma, the group velocity is:
(A)
proportional to but not equal to the phase velocity
(B)
inversely proportional to the phase velocity
(C)
equal to the phase velocity
(D)
a constant
Check Answer
Option B
Q.No:8 JAM-2017
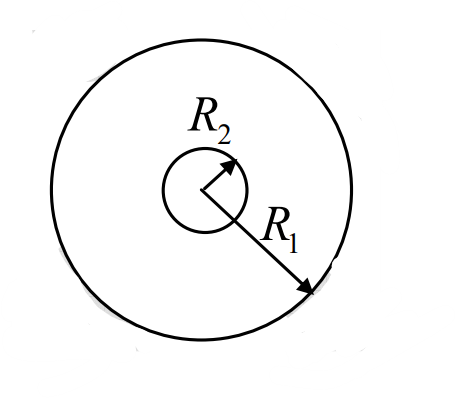
Consider two, single turn, co-planar, concentric coils of radii \(R_1\) and \(R_2\) with \(R_1\gg R_2\). The mutual inductance between the two coils is proportional to
(A)
\(\frac{R_1}{R_2}\)
(B)
\(\frac{R_2}{R_1}\)
(C)
\(\frac{R_2^2}{R_1}\)
(D)
\(\frac{R_1^2}{R_2}\)
Check Answer
Option C
Q.No:9 JAM-2017
The electric field of an electromagnetic wave is given by \(\vec{E}=(2\hat{k}-2\hat{j})\times 10^{-3} sin[10^7(x+2y+3z-\beta t)]\). The value of \(\beta\) is \(c\) is the speed of light):
(A)
\(\sqrt{14}c\)
(B)
\(\sqrt{12}c\)
(C)
\(\sqrt{10}c\)
(D)
\(\sqrt{7}c\)
Check Answer
Option A
Q.No:10 JAM-2017
A rectangular loop of dimension \(L\) and width \(w\) moves with a constant velocity \(v\) away from an infinitely long straight wire carrying a current \(I\) in the plane of the loop as shown in the figure below. Let \(R\) be the resistance of the loop. What is the current in the loop at the instant the near–side is at a distance \(r\) from the wire?
(A)
\(\frac{\mu_o I L}{2\pi R}\frac{w v}{r[r+2w]}\)
(B)
\(\frac{\mu_0 I L}{2 \pi R} \frac{w v}{r(2r+w)}\)
(C)
\(\frac{\mu_o I L}{2\pi R}\frac{w v}{r[r+w]}\)
(D)
\(\frac{\mu_o I L}{2\pi R}\frac{w v}{2r[r+w]}\)
Check Answer
Option C
Q.No:11 JAM-2017
Consider a circular parallel plate capacitor of radius \(R\) with separation \(d\) between the plates \((d\ll R)\). The plates are placed symmetrically about the origin. If a sinusoidal voltage \(V=V_0 \hspace{0.5mm} sin \hspace{0.5mm}\omega t\) is applied between the plates, which of the following statement(s) is
(are) true?
(A)
The maximum value of the Poynting vector at \(r=R\) is \(\frac{V_0^2\epsilon_o \omega R}{4d^2}\)
(B)
The average energy per cycle flowing out of the capacitor is zero
(C)
The magnetic field inside the capacitor is constant
(D)
The magnetic field lines inside the capacitor are circular with the curl being independent of \(r\) .
Check Answer
Option A,B,C
Q.No:12 JAM-2017
The wave number of an electromagnetic wave incident on a metal surface is \((20\pi+750i)m^{-1}\) inside the metal, where \(i=\sqrt{-1}\). The skin depth of the wave in the metal is __________________.
(Specify your answer in mm to two digits after the decimal point)
Check Answer
Ans 1.30-1.36
Q.No:13 JAM-2018
A rectangular loop of dimensions \(l\) and \(w\) moves with a constant speed of \(v\) through a region containing a uniform magnetic field B directed into the paper and extending a distance of \(4w\). Which of the following figures correctly represents the variation of emf (\(\epsilon\)) with the position (x) of
the front end of the loop?
Check Answer
Option C
Q.No:14 JAM-2018
A long solenoid is carrying a time dependent current such that the magnetic field inside has the form \(\vec{B}(t)=B_0t^2 \hat{k}\), where \(\hat{k}\) is along the axis of the solenoid. The displacement current at the point \(P\) on a circle of radius \(r\) in a plane perpendicular to the axis
(A)
is inversely proportional to \(r\) and radially outward.
(B)
is inversely proportional to \(r\) and tangential.
(C)
increases linearly with time and is tangential.
(D)
is inversely proportional to \(r^2\) and tangential.
Check Answer
Option B
Q.No:15 JAM-2018
An infinitely long solenoid, with its axis along \(\hat{k}\), carries a current \(I\). In addition there is a uniform
line charge density \(\lambda\) along the axis. If \(\vec{S}\) is the energy flux, in cylindrical coordinates \((\hat{\rho}, \hat{\phi}, \hat{k})\), then
(A)
\(\vec{S}\) is along \(\hat{\rho}\)
(B)
\(\vec{S}\) is along \(\hat{k}\)
(C)
\(\vec{S}\) has non zero components along \(\hat{\rho}\) and \(\hat{k}\)
(D)
\(\vec{S}\) is along \(\hat{\rho}\times \hat{k}\)
Check Answer
Option D
Q.No:16 JAM-2018
Consider an electromagnetic plane wave
\(\vec{E}=E_0(\hat{i}+b\hat{j}) cos [\frac{2\pi}{\lambda}\{ct-(x-\sqrt{3}y)\}]\), where \(\lambda\) is the wavelength, \(c\) is the speed of light and \(b\) is a constant. The value of \(b\) is _________________.
(Specify your answer upto two digits after the decimal point.)
Check Answer
Ans 0.55-0.59
Q.No:17 JAM-2019
Consider the normal incidence of a plane electromagnetic wave with electric field given by \(\vec{E}=E_0\) exp \([i(k_1z-\omega t )]\hat{x}\) over an interface at \(z=0\) separating two media [wave velocities \(v_1\) and \(v_2\) \((v_2>v_1)\) and \(k_1\) and \(k_2\), respectively] as shown in figure. The magnetic field vector of the reflected wave is
(\(\omega\) is the angular frequency)
(A)
\(\frac{E_0}{v_1}\) exp \([i(k_1 z-\omega t)]\hat{y}\)
(B)
\(\frac{E_0}{v_1}\) exp \([i(-k_1 z-\omega t)]\hat{y}\)
(C)
\(\frac{-E_0}{v_1}\) exp \([i(-k_1 z-\omega t)]\hat{y}\)
(D)
\(\frac{-E_0}{v_1}\) exp \([i(k_1 z-\omega t)]\hat{y}\)
Check Answer
Option C
Q.No:18 JAM-2020
A thin conducting square loop of side L is placed in the first quadrant of the xy-plane with one of the vertices at the origin. If a changing magnetic field \(\vec{B}(t)=\beta_0(5zyt \hat{x}+zxt \hat{y}+3y^2 t \hat{z})\) is applied, where \(\beta_0\) is a constant, then the magnitude of the induced electromotive force in the loop is
(A)
\(4\beta_0 L^4\)
(B)
\(3\beta_0 L^4\)
(C)
\(2\beta_0 L^4\)
(D)
\(\beta_0 L^4\)
Check Answer
Option D
Q.No:19 JAM-2020
For electric and magnetic fields, \(\vec{E}\) and \(\vec{B}\) due to a charge density \(\rho(\vec{r},t)\) and a current density \(\vec{J}(\vec{r},t)\) which of the following relations is/are always correct?
(A)
\(\vec{\nabla} \times \vec{E}=0\)
(B)
\(\vec{\nabla} \cdot \vec{B}=0\)
(C)
\(\vec{\nabla} \cdot \vec{J}-\frac{\partial \rho}{\partial t}=0\)
(D)
\(\vec{F}=q(\vec{E}+\vec{v}\times \vec{B})\), where \(\vec{F}\) is the force on a particle with charge \(q\) moving with velocity \(\vec{v}\)
Check Answer
Option B,D
Q.No:20 JAM-2021
The electric field of an electromagnetic wave has the form \(\vec{E}=E_0 cos (\omega t-kz)\hat{i}\). At \(t=0\), a test particle of charge \(q\) is at \(z=0\), and has velocity \(\vec{v}=0.5c\hat{k}\), where \(c\) is the speed of light. The total instantaneous force on the particle is
(A)
\(\frac{qE_0}{2}\hat{i}\)
(B)
\(\frac{qE_0}{\sqrt{2}}(\hat{i}+\hat{j})\)
(C)
\(\frac{qE_0}{2}(\hat{i}-\hat{k})\)
(D)
Zero
Check Answer
Option A
Q.No:21 JAM-2021
The expression for the magnetic field that induces the electric field \(\vec{E}=K(yz\hat{i}+3z\hat{j}+4y\hat{k}) cos (\omega t)\) is
(A)
\(-\frac{k}{\omega}(\hat{i}+y\hat{j}-z\hat{k}) \hspace{0.5mm}sin(\omega t)\)
(B)
\(-\frac{k}{\omega}(\hat{i}+y\hat{j}+z\hat{k}) \hspace{0.5mm}sin(\omega t)\)
(C)
\(-\frac{k}{\omega}(\hat{i}-y\hat{j}+z\hat{k}) \hspace{0.5mm}sin(\omega t)\)
(D)
\(-\frac{k}{\omega}(\hat{i}+y\hat{j}+z\hat{k}) \hspace{0.5mm}sin(\omega t)\)
Check Answer
Option A
Q.No:22 JAM-2021
A small conducting square loop of side \(l\) is placed inside a concentric large conducting square loop of side \(L(L\gg l)\). The value of mutual inductance of the system is expressed as \(\frac{n\mu_0 l^2}{\pi L}\). The value of \(n\) is __________________ (Round off to two decimal places).
Check Answer
Ans 2.80-2.85
Q.No:23 JAM-2022
The current through a series \(RL\) circuit, subjected to a constant emf \(\epsilon\), , obeys \(L\frac{di}{dt}+iR=\epsilon\). Let \(L=1\)mH, \(R=1k\Omega\) and \(\epsilon =1\)V.The initial condition is \(i(0)=0\). At \(t=1\mu\)s, the current in mA is
(A)
\(1-2e^{-2}\)
(B)
\(1-2e^{-1}\)
(C)
\(1-e^{-1}\)
(D)
\(2-2e^{-1}\)
Check Answer
Option C
Q.No:24 JAM-2022
A circular loop of wire with radius \(R\) is centered at the origin of the xy-plane. The magnetic field at a point within the loop is, \(\vec{B}(\rho , \phi , z,t)=k\rho^3 t^3 \hat{z}\), where \(k\) is a positive constant of appropriate dimensions. Neglecting the effects of any current induced in the loop, the magnitude of the induced emf in the loop at time \(t\) is
(A)
\(\frac{6\pi k t^2 R^5}{5}\)
(B)
\(\frac{5\pi k t^2 R^5}{6}\)
(C)
\(\frac{3\pi k t^2 R^5}{2}\)
(D)
\(\frac{\pi k t^2 R^5}{2}\)
Check Answer
Option A
Q.No:25 JAM-2022
A linearly polarized light beam travels from origin to point A (1,0,0). At the point A, the light is reflected by a mirror towards point B (1, -1, 0). A second mirror located at point B then reflects the light towards point C (1, -1, 1). Let \(\hat{n}(x,y,z)\) represent the direction of polarization of light at \((x,y,z)\).
(A)
If \(\hat{n}(0,0,0)=\hat{y}\), then \(\hat{n}(1,-1,1)=\hat{x}\)
(B)
If \(\hat{n}(0,0,0)=\hat{z}\), then \(\hat{n}(1,-1,1)=\hat{y}\)
(C)
If \(\hat{n}(0,0,0)=\hat{y}\), then \(\hat{n}(1,-1,1)=\hat{y}\)
(D)
If \(\hat{n}(0,0,0)=\hat{z}\), then \(\hat{n}(1,-1,1)=\hat{x}\)
Check Answer
Option A,B
Q.No:26 JAM-2022
The electric field associated with an electromagnetic radiation is given by \(E=a(1+cos \omega_1 t)cos \omega_2 t\). Which of the following frequencies are present in the field?
(A)
\(\omega_1\)
(B)
\(\omega_1 +\omega_2\)
(C)
\(|\omega_1 -\omega_2|\)
(D)
\(\omega_2\)
Check Answer
Option B,C,D
Q.No:27 JAM-2022
A current density for a fluid flow is given by,
\[\vec{J}(x,y,z,t)=\frac{8e^t}{(1+x^2+y^2+z^2)}\hat{x}\]
At time \(t = 0\), the mass density \(\rho(x,y,z,0)=1\).
Using the equation of continuity, \(\rho(1,1,1,1)\) is found to be _______________ (Round off to 2 decimal places).
Check Answer
Ans 2.70-2.74
Q.No:28 JAM-2023
A small bar magnet is dropped through different hollow copper tubes with same length and inner diameter but with different outer diameter. The variation in the time (t) taken for the magnet to reach the bottom of the tube depends on its wall thickness (d) as
Check Answer
Option C
Q.No:29 JAM-2023
Suppose the divergence of magnetic field \(\vec{B}\) is nonzero and is given as \(\vec{\nabla} \cdot \vec{B}= \mu_0 \rho_m \), where \(\mu_0\) is the permeability of vacuum and \(\rho_m\) is the magnetic charge density. If the corresponding magnetic current density is \(\vec{J}_m\), then the\(\vec{\nabla} \times \vec{E}\)
of the electric field \(\vec{E}\) is
A) \(\vec{J}_m - \frac{\partial \vec{B}}{\partial t}\)
B) \(\mu_0 \vec{J}_m - \frac{\partial \vec{B}}{\partial t}\)
C) \(-\vec{J}_m - \frac{\partial \vec{B}}{\partial t}\)
D) \(-\mu_0 \vec{J}_m - \frac{\partial \vec{B}}{\partial t}\)
Check Answer
Option D
Q.No:30 JAM-2023
In a dielectric medium of relative permittivity 5, the amplitudes of the displacement current and conduction current are equal for an applied sinusoidal voltage of frequency \(f\) = 1 MHz. The value of conductivity (in \(\Omega^{-1} m^{-1}\)) of the medium at this frequency is
A) \(2.78 \times 10^{-4}\)
B) \(2.44 \times 10^{-4}\)
C) \(2.78 \times 10^{-3}\)
D) \(2.44 \times 10^{-3}\)
Check Answer
Option A
Q.No:31 JAM-2023
A wave travelling along the x-axis with y representing its displacement is described by (\(v\) is the speed of the wave)
A) \(\frac{\partial y}{\partial x}+\frac{1}{v} \frac{\partial y}{\partial t}=0\)
B) \(\frac{\partial y}{\partial x}-\frac{1}{v} \frac{\partial y}{\partial t}=0\)
C) \(\frac{\partial^2y}{\partial x^2}+\frac{1}{v^2} \frac{\partial^2y}{\partial t^2}=0\)
D) \(\frac{\partial^2y}{\partial x^2}-\frac{1}{v^2} \frac{\partial^2y}{\partial t^2}=0\)
Check Answer
Option A,B,D
Q.No:32 JAM-2023
A conducting wire AB of length m has resistance of 1.6 \(\Omega\). It is connected to a voltage source of 0.5 V with negligible resistance as shown in the figure. The corresponding electric and magnetic fields give Poynting vectors \(\vec{S} (\vec{r})\) all around the wire. Surface integral \(\int \vec{S} \cdot d \vec{a}\) is calculated over a virtual sphere of diameter 0.2 m with its centre on the wire, as shown. The value of the integral is ________________W (rounded off to three decimal places)
Check Answer
Ans 0.030-0.033
Q.No:33 JAM-2024
A plane electromagnetic wave is incident on an interface AB separating two media (refractive indices \(n_1 = 1.5\) and \(n_2 = 2.0\)) at Brewster angle \(\theta_B\), as schematically shown in the figure. The angle \(\alpha\) (in degrees) between the reflected wave and the refracted wave is:
A) 120
B) 116
C) 90
D) 74
Check Answer
Option C
Q.No:34 JAM-2024
If the electric field of an electromagnetic wave is given by,
\[
\vec{E} = (4\hat{x} + 3\hat{y})e^{i(\omega t + ax - 600y)},
\]
then the value of \(a\) is:
(all values are in the SI units)
A) 450
B) -450
C) 800
D) -800
Check Answer
Option A
Q.No:35 JAM-2024
A \(15.7 \text{mW}\) laser beam has a diameter of \(4 \text{mm}\). If the amplitude of the associated magnetic field is expressed as \(\frac{A}{\sqrt{\varepsilon_0 c^3}}\), the value of \(A\) is:
\(\varepsilon_0\) is the free space permittivity and \(c\) is the speed of light)
A) 50
B) 35.4
C) 100
D) 70.8
Check Answer
Option A
Q.No:36 JAM-2024
Suppose that there is a dispersive medium whose refractive index depends on the wavelength as given by \( n(\lambda) = n_0 + \frac{a}{\lambda^2} - \frac{b}{\lambda^4} \). The value of \( \lambda \) at which the group and phase velocities would be the same, is:
A) \( \sqrt{\frac{2b}{a}} \)
B) \( \sqrt{\frac{b}{2a}} \)
C) \( \sqrt{\frac{3b}{a}} \)
D) \( \sqrt{\frac{b}{3a}} \)
Check Answer
Option A
Q.No:37 JAM-2024
A collimated light beam of intensity \( I_0 \) is incident normally on an air-dielectric (refractive index 2.0) interface. The intensity of the reflected light is ____________________ \( I_0 \). (Rounded off to two decimal places)
Check Answer
Ans 0.10-0.12
Q.No:38 JAM-2024
A time dependent magnetic field inside a long solenoid of radius \( 0.05m \) is given by \( \mathbf{B}(t) = B_0 \sin \omega t \hat{z} \). If \( \omega=100rad/s \) and \( B_0=0.98Weber/m^2 \), then the amplitude of the induced electric field at a distance of \( 0.07m \) from the axis of the solenoid is __________________\( V/m \). (Rounded off to two decimal places)
Check Answer
Ans 1.71 -1.75
Q.No:39 JAM-2025
An unpolarized light ray passing through air (refractive index \(n_a = 1\))
is incident on a glass slab (refractive index \(n_g = \sqrt{3}\))
at an angle of \(60^\circ\), as shown in the figure.
The amplitude of the in-plane (x–y) electric field component of the
incident light is 4 V/m and the amplitude of the out-of-plane (z)
electric field component is 3 V/m.
After passing through the glass slab, the electric field amplitude
(in V/m) of the light is
A) 5
B) 4
C) 7
D) 3
Check Answer
Option B
Q.No:40 JAM-2025
Consider a slowly charging parallel plate capacitor (distance between the plates is d)
having circular plates each with an area A, as shown in the figure.
An electric field of magnitude
\[
E = E_0 \sin(\omega t)
\]
exists between the plates while charging.
The associated magnitude of the magnetic field B at the periphery (outer edge)
of the capacitor is
(Neglect fringe effects)
A) \(
\frac{1}{2c^2}\sqrt{\frac{A}{\pi}}\,E_0\,\omega \cos(\omega t)
\)
B) \(
\frac{1}{2c^2}\sqrt{\frac{A}{\pi}}\,E_0\,\omega \sin(\omega t)
\)
C) \(
\frac{1}{c^2}\sqrt{\frac{A}{\pi}}\,E_0\,\omega \cos(\omega t)
\)
D) \(
\frac{1}{c^2}\sqrt{\frac{A}{\pi}}\,E_0\,\omega \sin(\omega t)
\)
Check Answer
Option A
Q.No:41 JAM-2025
For an electromagnetic wave, consider an electric field
\[
\vec{E} = E_0 e^{-i[a(x+y)-\omega t]}\,\hat{k}.
\]
The corresponding magnetic field \(\vec{B}\) is
(\(E_0, a, \omega\) are constants of appropriate dimensions and
\(c\) is the speed of light)
A) \(
\frac{1}{c\sqrt{2}}\,E_0 e^{-i[a(x+y)-\omega t]}(\hat{i}-\hat{j})
\)
B) \(
\frac{1}{c\sqrt{2}}\,E_0 e^{-i[a(x+y)-\omega t]}(\hat{i}+\hat{j})
\)
C) \(
\frac{1}{c\sqrt{2}}\,E_0 e^{-i[a(x+y)-\omega t]}(-\hat{i}-\hat{j})
\)
D) \(
\frac{1}{c\sqrt{2}}\,E_0 e^{-i[a(x+y)-\omega t]}(-\hat{i}+\hat{j})
\)
Check Answer
Option A
Q.No:42 JAM-2025
Identify which of the following wave functions describe(s) travelling wave(s).
(\(A_0, B_0, a,\) and \(b\) are positive constants of appropriate dimensions)
A) \(
\psi(x,t) = A_0 (x + t)^2
\)
B) \(
\psi(x,t) = A_0 \sin(ax^2 + bt^2)
\)
C) \(
\psi(x,t) = \frac{A_0}{B_0 (x - t)^2 + 1}
\)
D) \(
\psi(x,t) = A_0 e^{(ax + bt)^2}
\)
