Q.No:1 GATE-2012
A particle of mass \(m\) is attached to a fixed point \(O\) by a weightless inextensible string of length \(a\). It is rotating under the gravity as shown in the figure.
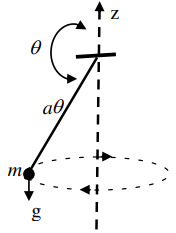
The Lagrangian of the particle is
\[
L(\theta, \phi)=\frac{1}{2}ma^2(\dot{\theta}^2+\sin^2{\theta\dot{\phi}^2})-mga\cos{\theta}
\]
where \(\theta\) and \(\phi\) are the polar angles. The Hamiltonian of the particle is
(A)
\(H=\frac{1}{2ma^2}\left(p_{\theta}^2+\frac{p_{\phi}^2}{\sin^2{\theta}}\right)-mga\cos{\theta}\)
(B)
\(H=\frac{1}{2ma^2}\left(p_{\theta}^2+\frac{p_{\phi}^2}{\sin^2{\theta}}\right)+mga\cos{\theta}\)
(C)
\(H=\frac{1}{2ma^2}\left(p_{\theta}^2+p_{\phi}^2\right)-mga\cos{\theta}\)
(D)
\(H=\frac{1}{2ma^2}\left(p_{\theta}^2+p_{\phi}^2\right)+mga\cos{\theta}\)
Check Answer
Option B
Q.No:2 GATE-2013
The Lagrangian of a system with one degree of freedom \(q\) is given by \(L=\alpha \dot{q}^2+\beta q^2\), where \(\alpha\) and \(\beta\) are non-zero constants. If \(p_q\) denotes the canonical momentum conjugate to \(q\) then which one of the following statements is CORRECT?
(A)
\(p_q=2\beta q\) and it is a conserved quantity.
(B)
\(p_q=2\beta q\) and it is not a conserved quantity.
(C)
\(p_q=2\alpha \dot{q}\) and it is a conserved quantity.
(D)
\(p_q=2\alpha \dot{q}\) and it is not a conserved quantity.
Check Answer
Option D
Q.No:3 GATE-2014
The Hamilton's canonical equations of motion in terms of Poisson Brackets are
(A)
\(\dot{q}=\{q, H\}; \dot{p}=\{p, H\}\)
(B)
\(\dot{q}=\{H, q\}; \dot{p}=\{H, p\}\)
(C)
\(\dot{q}=\{H, p\}; \dot{p}=\{H, q\}\)
(D)
\(\dot{q}=\{p, H\}; \dot{p}=\{q, H\}\)
Check Answer
Option A
Q.No:4 GATE-2014
Given that the linear transformation of a generalized coordinate \(q\) and the corresponding momentum \(p\),
\[
\begin{array}{c}
Q=q+4ap \\
P=q+2p
\end{array}
\]
is canonical, the value of the constant \(a\) is __________________.
Check Answer
Ans 0.24-0.26
Q.No:5 GATE-2014
The Hamiltonian of a particle of mass \(m\) is given by \(H=\frac{p^2}{2m}-\frac{\alpha q^2}{2}\). Which one of the following figures describes the motion of the particle in phase space?
Check Answer
Option D
Q.No:6 GATE-2015
The Lagrangian for a particle of mass \(m\) at a position \(\vec{r}\) moving with a velocity \(\vec{v}\) is given by \(L=\frac{m}{2}\vec{v}^2+C(\vec{r} \cdot \vec{v})-V(r)\), where \(V(r)\) is a potential and \(C\) is a constant. If \(\vec{p}_c\) is the canonical momentum, then its Hamiltonian is given by
(A)
\(\frac{1}{2m}(\vec{p}_c+C\vec{r})^2+V(r)\)
(B)
\(\frac{1}{2m}(\vec{p}_c-C\vec{r})^2+V(r)\)
(C)
\(\frac{p_c^2}{2m}+V(r)\)
(D)
\(\frac{1}{2m} p_c^2+Cr^2+V(r)\)
Check Answer
Option B
Q.No:7 GATE-2015
The Hamiltonian for a system of two particles of masses \(m_1\) and \(m_2\) at \(\vec{r}_1\) and \(\vec{r}_2\) having velocities \(\vec{\nu}_1\) and \(\vec{\nu}_2\) is given by \(H=\frac{1}{2}m_1 \nu_1^2+\frac{1}{2}m_2 \nu_2^2+\frac{C}{(\vec{r}_1-\vec{r}_2)^2} \hat{z}\cdot (\vec{r}_1\times \vec{r}_2)\), where \(C\) is a constant. Which one of the following statements is correct?
(A)
The total energy and total momentum are conserved
(B)
Only the total energy is conserved
(C)
The total energy and the \(z\)-component of the total angular momentum are conserved
(D)
The total energy and total angular momentum are conserved
Check Answer
Option C
Q.No:8 GATE-2017
The phase space trajectory of an otherwise free particle bouncing between two hard walls elastically in one dimension is a
(A)
straight line
(B)
parabola
(C)
rectangle
(D)
circle
Check Answer
Option C
Q.No:9 GATE-2018
A particle moves in one dimension under a potential \(V(x)=\alpha |x|\) with some non-zero total energy. Which one of the following best describes the particle trajectory in the phase space?
Check Answer
Option A
Q.No:10 GATE-2018
For the transformation
\[
Q=\sqrt{2q}e^{-1+2\alpha}\cos{p}, P=\sqrt{2q}e^{-\alpha-1}\sin{p}
\]
(where \(\alpha\) is a constant) to be canonical, the value of \(\alpha\) is ___________.
Check Answer
Ans 2
Q.No:11 GATE-2019
Consider a transformation from one set of generalized coordinate and momentum \((q, p)\) to another set \((Q, P)\) denoted by,
\[
Q=pq^s; P=q^r
\]
where \(s\) and \(r\) are constants. The transformation is canonical if
(A)
\(s=0\) and \(r=1\)
(B)
\(s=2\) and \(r=-1\)
(C)
\(s=0\) and \(r=-1\)
(D)
\(s=2\) and \(r=1\)
Check Answer
Option B
Q.No:12 GATE-2019
The Hamiltonian for a particle of mass \(m\) is \(H=\frac{p^2}{2m}+kqt\) where \(q\) and \(p\) are the generalized coordinate and momentum, respectively, \(t\) is time and \(k\) is a constant. For the initial condition, \(q=0\) and \(p=0\) at \(t=0\), \(q(t)\propto t^{\alpha}\). The value of \(\alpha\) is _____________
Check Answer
Ans 3
Q.No:13 GATE-2019
A ball bouncing off a rigid floor is described by the potential energy function
\[
\begin{array}{lll}
V(x) & =mgx & \text{for }x>0 \\
& \infty & \text{for }x\leq 0
\end{array}
\]
Which of the following schematic diagrams best represents the phase space plot of the ball?
Check Answer
Option B
Q.No:14 GATE-2019
Consider the Hamiltonian \(H(q, p)=\frac{\alpha p^2 q^4}{2}+\frac{\beta}{q^2}\), where \(\alpha\) and \(\beta\) are parameters with appropriate dimensions, and \(q\) and \(p\) are the generalized coordinate and momentum, respectively. The corresponding Lagrangian \(L(q, \dot{q})\) is
(A)
\(\frac{1}{2\alpha} \frac{\dot{q}^2}{q^4}-\frac{\beta}{q^2}\)
(B)
\(\frac{2}{\alpha} \frac{\dot{q}^2}{q^4}+\frac{\beta}{q^2}\)
(C)
\(\frac{1}{\alpha} \frac{\dot{q}^2}{q^4}+\frac{\beta}{q^2}\)
(D)
\(-\frac{1}{2\alpha} \frac{\dot{q}^2}{q^4}+\frac{\beta}{q^2}\)
Check Answer
Option A
Q.No:15 GATE-2020
A small disc is suspended by a fiber such that it is free to rotate about the fiber axis (see figure). For small angular deflections, the Hamiltonian for the disc is given by
\[
H=\frac{p_{\theta}^2}{2I}+\frac{1}{2}\alpha\theta^2
\]
where \(I\) is the moment of inertia and \(\alpha\) is the restoring torque per unit deflection. The disc is subjected to angular deflections (\(\theta\)) due to thermal collisions from the surrounding gas at temperature \(T\) and \(p_{\theta}\) is the momentum conjugate to \(\theta\). The average and the root-mean-square angular deflection, \(\theta_{avg}\) and \(\theta_{rms}\), respectively are
(A)
\(\theta_{avg}=0\) and \(\theta_{rms}=\left(\frac{k_B T}{\alpha}\right)^{3/2}\)
(B)
\(\theta_{avg}=0\) and \(\theta_{rms}=\left(\frac{k_B T}{\alpha}\right)^{1/2}\)
(C)
\(\theta_{avg}\neq 0\) and \(\theta_{rms}=\left(\frac{k_B T}{\alpha}\right)^{1/2}\)
(D)
\(\theta_{avg}\neq 0\) and \(\theta_{rms}=\left(\frac{k_B T}{\alpha}\right)^{3/2}\)
Check Answer
Option B
Q.No:16 GATE-2020
Let \(p\) be the momentum conjugate to the generalized coordinate \(q\). If the transformation
\[
\begin{array}{l}
Q=\sqrt{2}q^m \cos{p} \\
P=\sqrt{2}q^m \sin{p}
\end{array}
\]
is canonical, then \(m=\) __________.
Check Answer
Ans 0.5
Q.No:17 GATE-2020
Consider the Lagrangian \(L=a\left(\frac{dx}{dt}\right)^2+b\left(\frac{dy}{dt}\right)^2+cxy\), where \(a, b\) and \(c\) are constants. If \(p_x\) and \(p_y\) are the momenta conjugate to the coordinates \(x\) and \(y\) respectively, then the Hamiltonian is
(A)
\(\frac{p_x^2}{4a}+\frac{p_y^2}{4b}-cxy\)
(B)
\(\frac{p_x^2}{2a}+\frac{p_y^2}{2b}-cxy\)
(C)
\(\frac{p_x^2}{2a}+\frac{p_y^2}{2b}+cxy\)
(D)
\(\frac{p_x^2}{a}+\frac{p_y^2}{b}+cxy\)
Check Answer
Option A
Q.No:18 GATE-2021
If \(\vec{a}\) and \(\vec{b}\) are constant vectors, \(\vec{r}\) and \(\vec{p}\) are generalized positions and conjugate momenta, respectively, then for the transformation \(Q=\vec{a}\cdot \vec{p}\) and \(P=\vec{b}\cdot \vec{r}\) to be canonical, the value of \(\vec{a}\cdot \vec{b}\) (in integer) is _____________.
Check Answer
Ans (-1)
Q.No:19 GATE-2021
Consider a point charge \(+Q\) of mass \(m\) suspended by a massless, inextensible string of length \(l\) in free space (permittivity \(\varepsilon_0\)) as shown in the figure. It is placed at a height \(d\) (\(d>l\)) over an infinitely large, grounded conducting plane. The gravitational potential energy is assumed to be zero at the position of the conducting plane and is positive above the plane.
If \(\theta\) represents the angular position and \(p_{\theta}\) its corresponding canonical momentum, then the correct Hamiltonian of the system is
(A)
\(\frac{p_{\theta}^2}{2ml^2}-\frac{Q^2}{16\pi \varepsilon_0(d-l\cos{\theta})}-mg(d-l\cos{\theta})\)
(B)
\(\frac{p_{\theta}^2}{2ml^2}-\frac{Q^2}{8\pi \varepsilon_0(d-l\cos{\theta})}+mg(d-l\cos{\theta})\)
(C)
\(\frac{p_{\theta}^2}{2ml^2}-\frac{Q^2}{8\pi \varepsilon_0(d-l\cos{\theta})}-mg(d-l\cos{\theta})\)
(D)
\(\frac{p_{\theta}^2}{2ml^2}-\frac{Q^2}{16\pi \varepsilon_0(d-l\cos{\theta})}+mg(d-l\cos{\theta})\)
Check Answer
Option D
Q.No:20 GATE-2022
If \((\dot{x}\dot{y}+\alpha xy)\) is a constant of motion of a two-dimensional isotropic harmonic oscillator with Lagrangian
\[
L=\frac{m(\dot{x}^2+\dot{y}^2)}{2}-\frac{k(x^2+y^2)}{2}
\]
then \(\alpha\) is
(a)
\(+\frac{k}{m}\)
(b)
\(-\frac{k}{m}\)
(c)
\(-\frac{2k}{m}\)
(d)
\(0\)
Check Answer
Option a
Q.No:21 GATE-2022
A system with time independent Hamiltonian \(H(q, p)\) has two constants of motion \(f(q, p)\) and \(g(q, p)\). Then which of the following Poisson brackets are always zero?
(a)
\(\{H, f+g\}\)
(b)
\(\{H, \{f, g\}\}\)
(c)
\(\{H+f, g\}\)
(d)
\(\{H, H+fg\}\)
Check Answer
Option a,b,d
Q.No:22 GATE-2022
In the action-angle variables \((I_1, I_2, \theta_1, \theta_2)\), consider the Hamiltonian \(H=4I_1 I_2\) and \(0\leq \theta_1, \theta_2<2\pi\). Let \(\frac{I_1}{I_2}=\frac{1}{2}\). Which of the following are possible plots of the trajectories with different initial conditions in \(\theta_1\)-\(\theta_2\) plane?
Check Answer
Option b,d
Q.No:23 GATE-2023
A particle of mass m is free to move on a frictionless horizontal two dimensional \((r,\theta)\) plane, and is acted upon by a force \(\vec{F}=-\frac{k}{2r^3} \hat{r}\) with \(k\) being a positive constant. If \(p_r\) and \(p_\theta\) are the generalised momenta corresponding to
\(r\) and \(\theta\) respectively, then what is the value of \(\frac{d p_r}{dt}\) ?
(A)
\(\frac{p_\theta ^2 -2mk}{2mr^3}\)
(B)
\(\frac{2p_\theta ^2 -mk}{mr^3}\)
(C)
\(\frac{p_\theta ^2 -2mk}{mr^3}\)
(D)
\(\frac{2p_\theta ^2 -mk}{2mr^3}\)
Check Answer
Option D
Q.No:24 GATE-2024
cIf \( F_1(Q, q) = Qq \) is the generating function of a canonical transformation from \( (p, q) \) to \( (P, Q) \), then which one of the following relations is correct?
(A) \(\frac{p}{P} = \frac{Q}{q}\)
(B) \(\frac{P}{p} = \frac{Q}{q}\)
(C) \(\frac{p}{P} = -\frac{Q}{q}\)
(D) \(\frac{P}{p} = -\frac{Q}{q}\)
Check Answer
Option C
Q.No:25 GATE-2024
Lagrangian of a particle of mass \( m \) is \( L = \frac{1}{2}m\dot{x}^2 - \lambda x^4 \), where \( \lambda \) is a positive constant. If the particle oscillates with total energy \( E \), then the time period of oscillations is
\[
a \int_{0}^{\left(\frac{E}{\lambda}\right)^{\frac{1}{4}}} \frac{dx}{\sqrt{\left(\frac{2}{m}\right)(E - \lambda x^4)}}
\]
The value of \( a \) is _____ (in integer).
Check Answer
Ans 4
Q.No:26 GATE-2024
Consider the Lagrangian \( L = m\dot{x}\dot{y} - m\omega_0^2xy \). If \( p_x \) and \( p_y \) denote the generalized momenta conjugate to \( x \) and \( y \), respectively, then the canonical equations of motion are
(A) \(\dot{x} = \frac{p_x}{m}, \quad \dot{p_x} = -m\omega_0^2x, \quad \dot{y} = \frac{p_y}{m}, \quad \dot{p_y} = -m\omega_0^2y\)
(B) \(\dot{x} = \frac{p_x}{m}, \quad \dot{p_x} = m\omega_0^2x, \quad \dot{y} = \frac{p_y}{m}, \quad \dot{p_y} = m\omega_0^2y\)
(C) \(\dot{x} = \frac{p_y}{m}, \quad \dot{p_x} = -m\omega_0^2y, \quad \dot{y} = \frac{p_x}{m}, \quad \dot{p_y} = -m\omega_0^2x\)
(D) \(\dot{x} = \frac{p_y}{m}, \quad \dot{p_x} = m\omega_0^2y, \quad \dot{y} = \frac{p_x}{m}, \quad \dot{p_y} = m\omega_0^2x\)
Check Answer
Option C
Q.No:27 GATE-2024
Let \( \rho(\vec{p}, \vec{q}, t) \) be the phase space density of an ensemble of a system. The Hamiltonian of the system is \( H(\vec{p}, \vec{q}) \). If \( \{A, B\} \) denotes the Poisson bracket of A and B, then
\[
\frac{d\rho}{dt} = 0
\]
implies
(A) \(\frac{\partial \rho}{\partial t} = 0\)
(B) \(\frac{\partial \rho}{\partial t} \propto \{ \rho, H \}\)
(C) \(\frac{\partial \rho}{\partial t} \propto \left\{ \rho, \frac{\vec{p} \cdot \vec{q}}{2} \right\}\)
(D) \(\frac{\partial \rho}{\partial t} \propto \left\{ \rho, \frac{\vec{q} \cdot \vec{q}}{2} \right\}\)
Check Answer
Option B
Q.No:28 GATE-2025
The Lagrangian of a particle of mass \(m\) and charge \(q\) moving in a uniform
magnetic field of magnitude \(2B\) that points in the \(z\)-direction is given by
\[
L = \frac{m}{2}v^{2} + qB(xv_y - yv_x),
\]
where \(v_x, v_y, v_z\) are the components of its velocity \(\vec{v}\).
If \(p_x, p_y, p_z\) denote the conjugate momenta in the \(x, y, z\) directions
and \(H\) is the Hamiltonian, which of the following option(s) is/are correct?
A) \(
\frac{dx}{dt} = \frac{1}{m}(p_x - qBy)
\)
B) \(
\frac{dp_x}{dt} = \frac{qB}{m}(p_y - qBx)
\)
C) \(
\frac{dp_y}{dt} = -\frac{qB}{m}(p_x + qBy)
\)
D) \(
H = \frac{1}{2m}\left[(p_x + qBy)^2 + (p_y - qBx)^2 + p_z^2\right]
\)
Check Answer
Option B,C,D
Q.No:29 GATE-2025
A bead is constrained to move along a long, massless, frictionless horizontal rod
parallel to the \(x\)-axis. The rod itself is moving vertically upward along the
\(z\)-direction against gravity with a constant speed, starting from \(z = 0\)
at \(t = 0\), and remains horizontal.
The conjugate momenta are denoted by \(p_x, p_y, p_z\) and the Hamiltonian by \(H\).
Which of the following option(s) is/are correct?
A) \(H\) is the total energy of the system and is conserved
B) \(H\) is the total energy of the system and is not conserved
C) \(H\) is not the total energy of the system, but it is conserved
D) \(H\) is not the total energy of the system and is not conserved
Check Answer
Option D
Q.No:30 GATE-2025
In a one-dimensional Hamiltonian system with position \(q\) and momentum \(p\),
consider the canonical transformation \((q,p) \rightarrow (Q,P)\) defined by
\[
Q = \frac{1}{p}, \qquad P = q\,p^{2}.
\]
Here \(Q\) and \(P\) are the new position and momentum, respectively.
Which of the following option(s) regarding the generating function \(F\) is/are correct?
A) \(F = F_1(q,Q) = \frac{q}{Q}\)
B) \(F = F_2(q,P) = \sqrt{Pq}\)
C) \(F = F_3(p,Q) = \frac{2p}{Q}\)
D) \(F = F_4(p,P) = \frac{P}{p}\)
Check Answer
Option A,D
Q.No:31 GATE-2025
The Hamiltonian for a one-dimensional system with mass \(m\), position \(q\) and
momentum \(p\) is
\[
H(p,q) = \frac{p^{2}}{2m} + q^{2} A(q),
\]
where \(A(q)\) is a real function of \(q\).
If the equation of motion is given by
\[
m\frac{d^{2}q}{dt^{2}} = -5 q A(q),
\]
then
\[
\frac{dA(q)}{dq} = n\,\frac{A(q)}{q}.
\]
Find the value of \(n\) (an integer).
