Q.No:1 JEST-2012
A jet of gas consists of molecules of mass \(m\), speed \(v\) and number density \(n\) all moving co-linearly. This jet hits a wall at an angle \(\theta\) to the normal. The pressure exerted on the wall by the jet assuming elastic collision will be
(a)
\(p=2mnv^2\cos^2{\theta}\)
(b)
\(p=2mnv^2\cos{\theta}\)
(c)
\(p=\sqrt{(3/2)}mnv\cos^2{\theta}\)
(d)
\(p=mnv^2\)
Check Answer
Option a
Q.No:2 JEST-2013
A small mass \(M\) hangs from a thin string and can swing like a pendulum. It is attached above the window of a car. When the car is at rest, the string hangs vertically. The angle made by the string with the vertical when the car has a constant acceleration \(a=1.2 m/s^2\) is approximately
(a)
\(1^{\circ}\)
(b)
\(7^{\circ}\)
(c)
\(15^{\circ}\)
(d)
\(90^{\circ}\)
Check Answer
Option b
Q.No:3 JEST-2014
Given the fundamental constants \(\hbar\) (Planck's constant), \(G\) (universal gravitation constant) and \(c\) (speed of light), which of the following has dimension of length?
(a)
\(\sqrt{\frac{\hbar G}{c^3}}\)
(b)
\(\sqrt{\frac{\hbar G}{c^5}}\)
(c)
\(\frac{\hbar G}{c^3}\)
(d)
\(\sqrt{\frac{\hbar G}{8\pi G}}\)
Check Answer
Option a
Q.No:4 JEST-2014
Two point objects A and B have masses \(1000 Kg\) and \(3000 Kg\) respectively. They are initially at rest with a separation equal to \(1 m\). Their mutual gravitational attraction then draws them together. How far from A's original position will they collide?
(c)
\(1/3 m\)
(c)
\(1/2 m\)
(c)
\(2/3 m\)
(c)
\(3/4 m\)
Check Answer
Option a
Q.No:5 JEST-2015
A chain of mass \(M\) and length \(L\) is suspended vertically with its lower end touching weighing scale. The chain is released and falls freely onto the scale. Neglecting the size of the individual links, what is the reading of the scale when a length \(x\) of the chain has fallen?
(a)
\(\frac{Mgx}{L}\)
(b)
\(\frac{2Mgx}{L}\)
(c)
\(\frac{3Mgx}{L}\)
(d)
\(\frac{4Mgx}{L}\)
Check Answer
Option c
Q.No:6 JEST-2015
A spring of force constant \(k\) is stretched by \(x\). It takes twice as much work to stretch a second spring by \(\frac{x}{2}\). The force constant of the second spring is,
(a)
\(k\)
(b)
\(2k\)
(c)
\(4k\)
(d)
\(8k\)
Check Answer
Option b
Q.No:7 JEST-2016
A cylindrical shell of mass \(m\) has an outer radius \(b\) and an inner radius \(a\). The moment of inertia of the shell about the axis of the cylinder is:
(A)
\(\frac{1}{2}m(b^2-a^2)\)
(B)
\(\frac{1}{2}m(b^2+a^2)\)
(C)
\(m(b^2+a^2)\)
(D)
\(m(b^2-a^2)\)
Check Answer
Option B
Q.No:8 JEST-2016
In Millikan's oil-drop experiment an oil drop of radius \(r\), mass \(m\) and charge \(q=6\pi \eta r(v_1+v_2)/E\) is moving upwards with a terminal velocity \(v_2\) due to an applied electric field of magnitude \(E\), where \(\eta\) is the coefficient of viscosity. The acceleration due to gravity is given by:
(A)
\(g=6\pi \eta rv_1/m\)
(B)
\(g=3\pi \eta rv_1/m\)
(C)
\(g=6\pi \eta rv_2/m\)
(D)
\(g=3\pi \eta rv_2/m\)
Check Answer
Option A
Q.No:9 JEST-2017
Water is poured at a rate of \(R m^3/hour\) from the top into a cylindrical vessel of diameter \(D\). The vessel has a small opening of area \(a\) (\(\sqrt{a}\ll D\)) at the bottom. What should be the minimum height of the vessel so that water does not overflow?
(A)
\(\infty\)
(B)
\(\frac{R^2}{2ga^2}\)
(C)
\(\frac{R^2}{2gaD^2}\)
(D)
\(\frac{8R^2}{\pi D^2 g^2}\)
Check Answer
Option B
Q.No:10 JEST-2017
A ball of mass \(0.1 kg\) and density \(2000 kg/m^3\) is suspended by a massless string of length \(0.5 m\) under water having density \(1000 kg/m^3\). The ball experiences a drag force, \(\vec{F}_d=-0.2(\vec{v}_b-\vec{v}_w)\), where \(\vec{v}_b\) and \(\vec{v}_w\) are the velocites of the ball and water respectively. What will be the frequency of small oscillations for the motion of pendulum, if the water is at rest?
Check Answer
Ans 3
Q.No:11 JEST-2017
Consider a point particle A of mass \(m_A\) colliding elastically with another point particle B of mass \(m_B\) at rest, where \(m_B/m_A=\gamma\). After collision, the ratio of the kinetic energy of particle B to the initial kinetic energy of particle A is given by
(A)
\(\frac{4}{\gamma+2+1/\gamma}\).
(B)
\(\frac{2}{\gamma+1/\gamma}\).
(C)
\(\frac{2}{\gamma+2-1/\gamma}\).
(D)
\(\frac{1}{\gamma}\).
Check Answer
Option A
Q.No:12 JEST-2017
A toy car is made from a rectangular block of mass \(M\) and four disk wheels of mass \(m\) and radius \(r\). The car is attached to a vertical wall by a massless horizontal spring with spring constant \(k\) and constrained to move perpendicular to the wall. The coefficient of static friction between the wheels of the car and the floor is \(\mu\). The maximum amplitude of oscillations of the car above which the wheels start slipping is
(A)
\(\frac{\mu g(M+2m)(M+4m)}{mk}\).
(B)
\(\frac{\mu g(M^2-m^2)}{Mk}\).
(C)
\(\frac{\mu g(M+m)^2}{2mk}\).
(D)
\(\frac{\mu g(M+4m)(M+6m)}{2mk}\).
Check Answer
Option D
Q.No:13 JEST-2018
A ball of mass \(m\) starting from rest, falls a vertical distance \(h\) before striking a vertical spring, which it compresses by a length \(\delta\). What is the spring constant of the spring? (Hint: Measure all the vertical distances from the point where the ball first touches the uncompressed spring, i.e., set this point as the origin of the vertical axis.)
(A)
\(\frac{2mg}{\delta^2}(h+\delta)\)
(B)
\(\frac{2mgh}{\delta^3}(h-\delta)\)
(C)
\(\frac{2mg}{\delta^2}(h-\delta)\)
(D)
\(\frac{2mg}{\delta^2}h\)
Check Answer
Option A
Q.No:14 JEST-2018
Consider a simple pendulum in three dimensional space. It consists of a string length \(l=20 cm\) and bob mass \(m=15 kg\) attached to it as shown in the figure below. The acceleration due to gravity is downwards as shown in the figure with a magnitude \(g=10 ms^{-2}\).
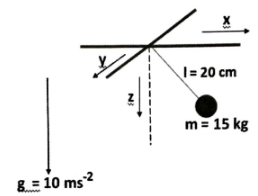
The pendulum is pulled in the \(x\)-\(z\) plane to a position where the string makes an angle \(\theta=\pi/3\) with the \(z\)-axis. It is then released with an angular velocity \(\Omega\) radians per second about the \(z\)-axis. What should be the value of \(\Omega\) in radians per second so that the angle the string makes with the \(z\)-axis does not change with time?
Check Answer
Ans 10
Q.No:15 JEST-2018
A block of mass \(M\) rests on a plane inclined at an angle \(\theta\) with respect to the horizontal. A horizontal force \(F=Mg\) is applied to the block. If \(\mu\) is the static friction between the block and the plane, the range of \(\theta\) so that the block remains stationary is
(A)
\(-\mu\leq \tan{\theta}\leq \mu\)
(B)
\(1-\mu\leq \cot{\theta}\leq 1+mu\)
(C)
\(\frac{1-\mu}{1+mu}\leq \tan{\theta}\leq \frac{1+\mu}{1-mu}\)
(D)
\(\frac{1-\mu}{1+mu}\leq \cot{\theta}\leq \frac{1+\mu}{1-mu}\)
Check Answer
Option
Q.No:16 JEST-2018
A ball comes in from the left with speed \(1\) (in arbitrary units) and causes a series of collisions. The other four balls shown the figure are initially at rest. The initial motion is shown below (the number in the circle indicate the object's relative mass). This initial velocities of the balls shown in the figure are represented as \([1, 0, 0, 0, 0]\).
A negative sign means that the velocity is directed to the left. All collisions are elastic. Which of the following indicates the velocities of the balls after all the collisions are completed?
(A)
\([-1/2, -1/2, 0, 0, 1/2]\)
(B)
\([-1/3, 0, 0, 0, 2/3]\)
(C)
\([-1/2, 0, 0, 0, 3/4]\)
(D)
\([-1/2, 0, 0, 0, 1/2]\)
Check Answer
Option B
Q.No:17 JEST-2019
Two objects of unit mass are thrown up vertically with a velocity of \(1 ms^{-1}\) at latitudes \(45^{\circ} N\) and \(45^{\circ} S\), respectively. The angular velocity of the rotation of Earth is given to be \(7.29 \times 10^{-5} s^{-1}\). In which direction will the objects deflect when they reach their highest point (due to Coriolis force)? Assume zero air resistance.
(A)
to the east in Northern hemisphere and west in Southern Hemisphere
(B)
to the west in Northern hemisphere and east in Southern Hemisphere
(C)
to the east in both hemispheres
(D)
to the west in both hemispheres
Check Answer
Option D
Q.No:18 JEST-2019
A bullet with initial speed \(v_0\) is fired at a log of wood. The resistive force by wood on the bullet is given by \(\eta v^{\alpha}\), where \(\alpha<1\). What is the time taken to stop the bullet inside the wood log?
(A)
\(\frac{m}{\eta}\frac{v_0^{\alpha-1}}{1-\alpha}\)
(B)
\(\frac{m}{\eta}\frac{v_0^{\alpha+1}}{\alpha+1}\)
(C)
\(\frac{m}{\eta}\frac{v_0^{1-\alpha}}{1-\alpha}\)
(D)
\(\frac{\eta}{m}\frac{v_0^{1-\alpha}}{1-\alpha}\)
Check Answer
Option C
Q.No:19 JEST-2019
A thin uniform steel chain is \(10 m\) long with a linear mass density of \(2 kg ~m^{-1}\). The chain hangs vertically with one end attached to a horizontal axle, having a negligibly small radius compared to its length. What is the work done (in \(N\text{-}m\)) to slowly wind up the chain on to the axle? The acceleration due to gravity is \(g=9.81 ms^{-2}\).
Check Answer
Ans 981
Q.No:20 JEST-2020
Two tuning forks A and B are struck instantaneously to obtain Lissajous figures. The figures go through a complete cycle in \(20 s\). Fork A is loaded slightly with wax, so that the cycle period changes to \(10 s\). If the frequency of fork B is \(256.10 Hz\), what is the frequency of fork A after loading?
(A)
\(256.00 Hz\)
(B)
\(256.05 Hz\)
(C)
\(256.15 Hz\)
(D)
\(256.20 Hz\)
Check Answer
Option A
Q.No:21 JEST-2020
A cleaning machine presses a circular mop of radius \(R=30 cm\) vertically down on a floor with a total force \(F=25 N\) and rotates it with a constant angular speed about the vertical axis passing through the centre of mop. If the force is distributed uniformly over the mop and if the coefficient of friction between the mop and the floor is \(\mu=0.25\), what is the value of torque in N-cm applied by the machine on the mop?
Check Answer
Ans 125
Q.No:22 JEST-2020
A small insect of mass \(m\) is sitting on the rim of a uniform circular horizontal disk of radius \(R\) and mass \(M\). The system is rotating at a constant angular velocity \(\omega_i\) about a frictionless vertical axis passing through the center of the disk. The insect started to crawl towards the center of the disk. Assume \(M/m=10\), and let the final angular velocity of the system, when the insect reaches the centre of the disk, be \(\omega_f\). What is the value of \(100 \omega_f/\omega_i\)?
Check Answer
Ans 120
Q.No:23 JEST-2021
A solid sphere and a solid cylinder, both of uniform mass density, start rolling down without slipping from rest from the same height along an inclined plane (see figure). Which one of the following statements is correct?
(A)
The sphere would reach the bottom faster.
(B)
The cylinder would reach the bottom faster.
(C)
The heavier one would reach the bottom faster if both have identical radii.
(D)
Both the objects would reach the bottom at the same time if their radii are identical.
Check Answer
Option A
Q.No:24 JEST-2021
If \(\vec{x}_A\) and \(\vec{x}_B\) are the position vectors of two points on a rigid body, which one of the following is NOT necessarily true?
(A)
\(\ddot{\vec{x}}_A-\ddot{\vec{x}}_B=0\)
(B)
\((\vec{x}_A-\vec{x}_B)\cdot \left(\dot{\vec{x}}_A-\dot{\vec{x}}_B\right)=0\)
(C)
\((\vec{x}_A-\vec{x}_B)\cdot \left(\ddot{\vec{x}}_A-\ddot{\vec{x}}_B\right)+|\dot{\vec{x}}_A-\dot{\vec{x}}_B|^2=0\)
(D)
\(\frac{d}{dt}|\vec{x}_A-\vec{x}_B|=0\)
Check Answer
Option A
Q.No:25 JEST-2021
A hollow sphere of radius \(R\), with a small hole at the bottom, is completely filled with a liquid of uniform density (see figure). The liquid drains out of the sphere through the hole at an uniform rate in time \(T\). Which one of the following graphs (A, B, C , D) qualitatively represents the height \(h\) of the center of mass (of sphere \(+\) liquid inside it), measured from the bottom of the sphere with time?
Check Answer
Option D
Q.No:26 JEST-2021
An aircraft flies over the North pole at a constant speed of \(900 \text{Km/hr}\). A small bob is hanging freely from the ceiling of the aircraft. What is the angle (in micro-radians) it makes with the Earth's radial direction? (Take the acceleration due to gravity to be \(9.81 \text{m}/\text{s}^2\)).
Check Answer
Ans 3707
Q.No:27 JEST-2021
A thin tube of length \(1080 \text{mm}\) and uniform cross-section is sealed at both ends, and placed horizontally on a table. At the exact center of the tube is a mercury (\(\text{Hg}\)) pellet of length \(180 \text{mm}\). The pressure of the air on both sides of the mercury pellet is \(P_0\). When the tube is held at an angle of \(60\) degrees with the vertical, the length of the air column above and below the \(\text{Hg}\) become \(480 \text{mm}\) and \(420 \text{mm}\), respectively. Assuming the temperature of the system to be constant, calculate the pressure \(P_0\) in \(\text{mm}\) of \(\text{Hg}\).
Check Answer
Ans 672
Q.No:28 JEST-2022
For a system of unit mass, the dynamical variables follow the relation \(\dot{x}^2=kx_0^2+\dot{x}_0^2-kx^2\) where, \(x\) is the position of the system at time \(t\), and \(x_0\) is its initial position. What is the force acting on the system?
(a)
\(-kx\)
(b)
\(-k(x-x_0)\)
(c)
\(-\frac{1}{2}k(x-x_0)\)
(d)
\(\frac{1}{2}k(x-x_0)^2\)
Check Answer
Option a
Q.No:29 JEST-2022
A cylinder of radius \(R\) is constrained to roll without slipping on a horizontal plane under the action of a constant force \(F\) applied \(d\) distance above the axis of the cylinder. In the process, it experiences a frictional force \(f\) at the point of contact (see figure). For what value of \(d\), the magnitude of \(f\) is minimum?
(a)
\(R/2\)
(b)
\(R\)
(c)
\(-R/2\)
(d)
\(-R\)
Check Answer
Option a
Q.No:30 JEST-2022
A small object A of mass \(m\) is free to slide on the inclined plane of a triangular block B of mass \(2m\) (see figure). Initially both the blocks are motionless. Block A starts sliding under the action of gravity from the highest point of block B. What is the speed of block B, when block A hits the floor?
(a)
\(\frac{1}{3}\sqrt{gl}\)
(b)
\(\frac{1}{2}\sqrt{gl}\)
(c)
\(\sqrt{gl}\)
(d)
\(\frac{2}{3}\sqrt{gl}\)
Check Answer
Option a
Q.No:31 JEST-2023
A rod of length \(l = 1\) meter is held on a frictionless horizontal surface at an angle of \(\theta= 60^\circ\) with the horizontal, as shown in the figure. Take the point of contact of the rod with the horizontal plane as the origin \((x = 0)\). As the support holding the rod is suddenly removed, the rod comes in contact with the horizontal surface. What will be the coordinate of the left end of the rod at the moment of contact?
(a) -0.15 m
(b) -0.5 m
(c)-0.2 m
(d) -0.25 m
Check Answer
Option d
Q.No:32 JEST-2023
Two particles of mass \(m\) and \(4\)m confined to move along the x-axis are subjected to the force \(F(x)=-kx\). At time \(t = 0\), the smaller mass \(m\) starts from rest at \(x_1(t = 0) = A\) and the larger mass \(4m\) starts from rest at \(x_2(t = 0) = -A\). The point on the x-axis where the first collision between the two particles occurs is:
(a) \(x=\frac{A}{2}\)
(b) \(x=-\frac{A}{2}\)
(c) \(x=-\frac{A}{4}\)
(d) \(x=0\)
Check Answer
Option b
Q.No:33 JEST-2023
The position and velocity vectors of a particle changes from \(\vec{R_1}\) to \(\vec{R_2}\) and \(\vec{v_1}\) to \(\vec{v_2}\) respectively as time flows from \(t_1\) to \(t_2\). If \(\vec{r}(t),\vec{v}(t)\) and \(\vec{a}(t)\) are the instantaneous position, velocity and acceleration vectors of the particle, compute the integral:
\[\vec{I}=\int_{t_1} ^{t_2} \hspace{1mm} \vec{r} \times \vec{a} \hspace{1mm} dt\]
Mark the correct answer.
(a) \(\vec{I}=\vec{R_2} \times \vec{v_2}-\vec{R_1} \times \vec{v_1}\)
(b) \(\vec{I}=0\)
(c) \(\vec{I}=\vec{R_1} \times \vec{v_1}-\vec{R_2} \times \vec{v_2}\)
(d) \(|\vec{I}|=|\vec{R_1} \times \vec{v_1}|+|\vec{R_2} \times \vec{v_2}|\)
Check Answer
Option a
Q.No:34 JEST-2024
A cylindrical rigid block has principal moments of inertia \( I \) about the symmetry axis and \( 2I \) about each of the perpendicular axes passing through the center of mass. At some instant, the components of angular momentum about the center of mass in the body-fixed principal axis frame is \( (l, l, l) \), with \( l > 0 \). What is the cosine of the angle between the angular momentum and the angular velocity?
(A) \( \frac{2\sqrt{2}}{3} \)
(B) \( \frac{2}{\sqrt{6}} \)
(C)\( \frac{2}{3} \)
(D) \( \frac{5}{3\sqrt{3}} \)
Check Answer
Option A
Q.No:35 JEST-2025
Consider a circular disk of radius \(R\) and mass \(M\) lying in the \(x\!-\!y\) plane,
with surface mass density
\[
\sigma(r) = \sigma_0 e^{-r^2/a^2},
\]
where \(r\) is the distance from the center of the disk.
What is the moment of inertia of the disk about the \(z\)-axis through its center?
(Consider \(R \gg a\).)
A) \(M a^2\)
B) \(\frac{1}{2} M a^2\)
C) \(6 M a^2\)
D) \(\frac{1}{3} M a^2\)
