Q.No:1 JAM-2015
A proton from outer space is moving towards earth with velocity \(0.99c\) as measured in earth’s
frame. A spaceship, traveling parallel to the proton, measures proton’s velocity to be \(0.97c\). The
approximate velocity of the spaceship, in the earth’s frame, is
(A)
\(0.2\hspace{0.3mm}c\)
(B)
\(0.3\hspace{0.3mm}c\)
(C)
\(0.4\hspace{0.3mm}c\)
(D)
\(0.5\hspace{0.3mm}c\)
Check Answer
Option D
Q.No:2 JAM-2015
A rod is moving with a speed of \(0.8c\) in a direction at \(60^\circ\) to its own length. The percentage contraction in the length of the rod is ______________.
Check Answer
Ans 8-9
Q.No:3 JAM-2015
X-rays of wavelength \(0.24\) nm are Compton scattered and the scattered beam is observed at an
angle of \(60^\circ\) relative to the incident beam. The Compton wavelength of the electron is \(0.00243\) nm. The kinetic energy of scattered electrons in \(eV\) is ______________.
Check Answer
Ans 25
Q.No:4 JAM-2016
A particle is moving in a plane with a constant radial velocity of \(12\) m/s and constant angular velocity of 2 rad/s. When the particle is at a distance \(r=8\)m from the origin, the magnitude of the instantaneous velocity of the particle in m/s is
(A)
\(8\sqrt{15}\)
(B)
\(20\)
(C)
\(2\sqrt{37}\)
(D)
\(10\)
Check Answer
Option B
Q.No:5 JAM-2017
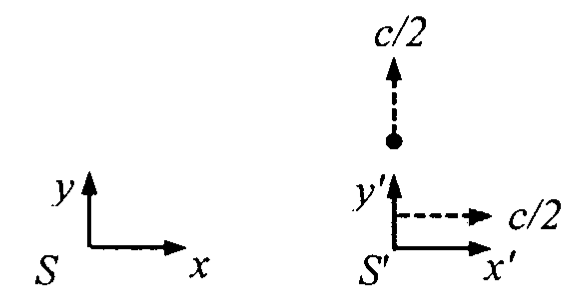
Consider an inertial frame \(S'\) moving at speed \(\frac{c}{2}\) away from another inertial frame S along the common \(x-x'\) axis, where c is the speed of light. As observed from \(S"\), a
particle is moving with speed \(\frac{c}{2}\) in the \(y'\) direction, , as shown in the figure. The speed of the particle as seen from S is:
(A)
\(\frac{c}{\sqrt{2}}\)
(B)
\(\frac{c}{2}\)
(C)
\(\frac{\sqrt{7}c}{4}\)
(D)
\(\frac{\sqrt{3}c}{5}\)
Check Answer
Option C
Q.No:6 JAM-2017
At \(t=0\), a particle of mass m having velocity \(v_0\) starts moving through a liquid kept in a horizontal tube and experiences a drag force \((F_d=-k\frac{dx}{dt}\). It covers a distance \(L\) before coming to rest. If the times taken to cover the distances \(L/2\) and \(L/4\) are \(t_2\) and \(t_4\) respectively, then the ratio \(t_2/t_2\) (ignoring gravity) is ____________ .
(Specify your answer to two digits after the decimal point)
Check Answer
Ans 2.35-2.50
Q.No:7 JAM-2018
Two vehicles A and B are approaching an observer \(O\) at rest with equal speed as shown in the figure. Both vehicles have identical sirens blowing at a frequency \(f_s\). The observer hears these sirens at frequency \(f_A\) and \(f_B\), respectively from the two vehicles. Which one of the following is
correct?
(A)
\(f_A=f_B<f_s\)
(B)
\(f_A=f_B>f_s\)
(C)
\(f_A>f_B>f_s\)
(D)
\(f_A<f_B<f_s\)
Check Answer
Option B
Q.No:8 JAM-2018
A particle of mass \(m\) is moving in a circular orbit given by \(x=R \hspace{1mm} cos (\omega t) ;y=R \hspace{1mm} sin (\omega t)\) as observed in an inertial frame \(S_1\). Another inertial frame \(S_2\) moves with uniform velocity \(\vec{v}=\omega R \hat{i}\) with respect to \(S_1\). \(S_1\) and \(S_2\) are related by Galilean transformation, such that the origins coincide at \(t=0\). The magnitude of the angular momentum of the particle at \(t=\frac{2\pi}{\omega}\), as observed in \(S_2\) about its origin, is expressed as \((mR^2\omega)x\). Then \(x\) is _____________.
(Specify your answer upto two digits after the decimal point.)
Check Answer
Ans 5.25-5.30 OR (-5.30-(-5.25))
Q.No:9 JAM-2018
Rod \(R_1\) has a rest length 1m and rod \(R_2\) has a rest length of 2m. \(R_1\) and \(R_2\) are moving with respect
to the laboratory frame with velocities \(+v\hat{i}\) and \(-v\hat{i}\), respectively. If \(R_2\) has a length of 1m in the
rest frame of \(R_1\), \(\frac{v}{c}\) is given by ____________.
(Specify your answer in seconds upto two digits after the decimal point.)
Check Answer
Ans 0.50-0.60
Q.No:10 JAM-2018
Two events \(E_1\) and \(E_2\) take place in an inertial frame \(S\) with respective time-space coordinates (in SI units): \(E_1(t_1=0, \vec{r}_1=0\) and \(E_2(t_2=0, x_2=10^8, y_2=0 ,z_2=0 \).Another inertial frame \(S'\) is moving with respect to \(S\) with a velocity \(\vec{v}=0.8 c\hat{i}\).The time difference \((t'_2-t'_1)\) as observed in \(S'\) frame is ________________ s.(c=\(3\times 10^8ms^{-1}\)
(Specify your answer in seconds upto two digits after the decimal point.)
Check Answer
Ans -0.46-(-0.42)
Q.No:11 JAM-2019
The amount of work done to increase the speed of an electron from \(c/3\) to \(2c/3\) is
(c =\(3\times 10^8\) m/s and rest mass of electron is 0.511 MeV)
(A)
\(56.50 \) keV
(B)
\(143.58\) keV
(C)
\(168.20\) keV
(D)
\(511.00\) keV
Check Answer
Option B
Q.No:12 JAM-2019
Which of the following statement(s) is/are true?
(A)
Newton’s laws of motion and Maxwell’s equations are both invariant under Lorentz transformations.
(B)
Newton’s laws of motion and Maxwell’s equations are both invariant under Galilean transformations.
(C)
Newton’s laws of motion are invariant under Galilean transformations and Maxwell’s equations are invariant under Lorentz transformations.
(D)
Newton’s laws of motion are invariant under Lorentz transformations and Maxwell’s equations are invariant under Galilean transformations.
Check Answer
Option C
Q.No:13 JAM-2020
Two objects of masses \(m\) and \(2m\) are moving at speeds of \(v\) and \(v/2\), respectively. After undergoing a completely inelastic collision, they move together with a speed of \(v/3\). The angle between the initial velocity vectors of the two objects is
(A)
\(60^\circ\)
(B)
\(120^\circ\)
(C)
\(45^\circ\)
(D)
\(90^\circ\)
Check Answer
Option B
Q.No:14 JAM-2021
Three events, \(E_1(ct=0 , x=0)\) , \(E_2(ct=0 , x=L)\) and \(E_3(ct=0 , x=-L)\) occur, as observed in an inertial frame \(S\).Frame \(S'\) is moving with a speed \(v\) along the positive
x-direction with respect to \(S\). In \(S'\), let \(t_1' ,t_2', t_3'\) be the respective times at which \(E_1 , E_2\), and \(E_3\) occurred. Then,
(A)
\(t_2'< t_1'<t_3'\)
(B)
\(t_1'= t_2'=t_3'\)
(C)
\(t_3'< t_1'<t_2'\)
(D)
\(t_3'< t_2'<t_1'\)
Check Answer
Option A
Q.No:15 JAM-2021
A particle is moving with a velocity \(0.8c\hat{j}\) (\(c\) is the speed of light) in an inertial frame \(S_1\). Frame \(S_2\) is moving with a velocity \(0.8c\hat{i}\) with respect to \(S_1\). Let \(E_1\) and \(E_2\) be the respective energies of the particle in the two frames. Then, \(\frac{E_2}{E_1}\) is _______________ (Round off to two decimal
places).
Check Answer
Ans 1.64-1.68
Q.No:16 JAM-2022
A rocket \((S')\) moves at a speed \(\frac{c}{2}\) m/s along the positive x-axis, where \(c\) is the speed of light. When it crosses the origin, the clocks attached to the rocket and the one with a stationary observer \((S)\) located at x= 0 are both set to zero. If \(S\) observes an event at \((x,t)\)), the same event occurs in the \(S'\) frame at
(A)
\(x'=\frac{2}{\sqrt{3}}(x-\frac{ct}{2})\) and \(t'=\frac{2}{\sqrt{3}}(t-\frac{x}{2c})\)
(B)
\(x'=\frac{2}{\sqrt{3}}(x+\frac{ct}{2})\) and \(t'=\frac{2}{\sqrt{3}}(t-\frac{x}{2c})\)
(C)
\(x'=\frac{2}{\sqrt{3}}(x-\frac{ct}{2})\) and \(t'=\frac{2}{\sqrt{3}}(t+\frac{x}{2c})\)
(D)
\(x'=\frac{2}{\sqrt{3}}(x+\frac{ct}{2})\) and \(t'=\frac{2}{\sqrt{3}}(t+\frac{x}{2c})\)
Check Answer
Option A
Q.No:17 JAM-2022
A rod with a proper length of 3 m moves along x-axis, making an angle of 300 with respect to the x-axis. If its speed is \(\frac{c}{2}\) m/s, where \(c\) is the speed of light, the change in length due to Lorentz contraction is ______________________ m (Round off to 2 decimal places).
(Use c=\(3\times 10^8\) m/s)
Check Answer
Ans (-0.31)-(-0.29) OR 0.29-0.31
Q.No: 18 JAM-2020
Two relativistic particles with opposite velocities collide head-on and come to rest by sticking with each other. Which of the following quantities is/are conserved in the collision?
(A)
Total momentum
(B)
Total energy
(C)
Total kinetic energy
(D)
Total rest mass
Check Answer
Option A,B
Q.No: 19 JAM-2023
A spacecraft has speed\(v_s=f \hspace{0.5mm} c\) with respect to the earth, where \(c\) is the speed of light in vacuum. An observer in the spacecraft measures the time of one complete rotation of the earth to be 48 hours. The value of \(f\) is ______________ (rounded off to
two decimal places).
Check Answer
Ans 0.85-0.88
Q.No: 20 JAM-2023
Three frames \(F_0, F_1\) and \(F_2\) are in relative motion. The frame \(F_0\) is at rest, \(F_1\) is moving with velocity \(v_1 \hat{i}\) with respect to \(F_0\) and \(F_2\) is moving with velocity \(v_2 \hat{i}\)
with respect to \(F_1\). A particle is moving with velocity \(v_3 \hat{i}\) with respect to \(F_2\). If \(v_1=v_2=v_3=c/2\), where \(c\) is the speed of light, the speed of the particle with respect to \(F_0\) is \(f \hspace{0.5mm} c\). The value of \(f\) is ______________(rounded off to two decimal places).
Check Answer
Ans 0.90-0.96
Q.No: 21 JAM-2023
A fission device explodes into two pieces of rest masses \(m\) and \(0.5m\) with no loss of energy into any other form. These masses move apart respectively with speeds \(\frac{c}{\sqrt{13}}\) and \(\frac{c}{2}\), with respect to the stationary frame. If the rest mass of the device is \(f \hspace{0.3mm} m\) then \(f\) is _____________________(rounded off to two decimal places).
Check Answer
Ans 1.60-1.64
Q.No: 22 JAM-2024
Given that the rest mass of electron is \(0.511\text{MeV}/c^2\), the speed (in units of \(c\)) of an electron with kinetic energy \(5.11\text{MeV}\) is closest to:
A) 0.996
B) 0.993
C) 0.990
D) 0.998
Check Answer
Option A
Q.No: 23 JAM-2024
The inertial frame \(S'\) is moving away from the inertial frame \(S\) with a speed \(v = 0.6c\) along the negative x-direction (see figure). The origins \(O'\) and \(O\) of the frames coincide at \(t = t' = 0\). As observed in the frame \(S'\), two events occur simultaneously at two points on the x'-axis with a separation of \(\Delta x' = 5m\). If \(\Delta t\) and \(\Delta x\) are the magnitudes of the time interval and the space interval, respectively, between the events in \(S\), then which of the following statements is(are) correct?
(c is \(3 \times 10^8 m/s\))
A) \(\Delta t = 12.5ns\)
B) \(\Delta t = 4.2ns\)
C) \(\Delta x = 10.6m\)
D) \(\Delta x = 6.25m\)
Check Answer
Option A,D
Q.No: 24 JAM-2024
An unstable particle created at a point \( P \) moves with a constant speed of \( 0.998c \) until it decays at a point \( Q \). If the lifetime of the particle in its rest frame is \( 632ns \), the distance between points \( P \) and \( Q \) is _____________ \( m \). (Rounded off to the nearest integer)
(\( c = 3 \times 10^8 m/s \))
Check Answer
Ans 2992-2994
Q.No: 25 JAM-2025
Consider a relativistic particle of rest mass 2m moving with speed v
along the x-direction. It collides with another relativistic particle
of rest mass m moving with the same speed but in the opposite direction.
These two particles coalesce to form one particle whose rest mass M is
____.
(\(\beta = v/c\), where c is the speed of light)
A) \(
m\sqrt{\frac{9-\beta^2}{1-\beta^2}}
\)
B) \(
2m\sqrt{\frac{3-\beta^2}{1-\beta^2}}
\)
C) \(
\frac{m}{2}\sqrt{\frac{9-\beta^2}{2-\beta^2}}
\)
D) \(
\frac{m}{4}\sqrt{\frac{1-\beta^2}{2-\beta^2}}
\)
Check Answer
Option A
Q.No: 26 JAM-2025
Two non-relativistic particles with masses \(m_1\) and \(m_2\) move with momenta
\(p_1\) and \(p_2\), respectively, in an inertial frame S.
In another inertial frame \(S'\), moving with a constant speed with respect
to S, the same particles are observed to have momenta \(p{_1}{'}\) and \(p{_2}{'}\),
respectively.
Galilean invariance implies that
A) \(m_2p{_1}{'}\) − \(m_1p{_2}{'}\) =\(m_2p_1\) − \(m_1p_2\)
B) \(m_2p{_1}{'}\) + \(m_1p{_2}{'}\) =\(m_2p_1\) + \(m_1p_2\)
C) \(m_1p{_1}{'}\) − \(m_2p{_2}{'}\) =\(m_1p_1\) − \(m_2p_2\)
D) \(m_1p{_1}{'}\) + \(m_2p{_2}{'}\) =\(m_1p_1\) + \(m_2p_2\)
