Q.No:1 JAM-2015
A system consists of \(N\) number of particles, \(N\gg 1\). Each particle can have only one of the two energies \(E_1\) or \(E_1+\varepsilon\) (\(\varepsilon>0\)). If the system is in equilibrium at a temperature \(T\), the average number of particles with energy \(E_1\) is
(A)
\(\frac{N}{2}\)
(B)
\(\frac{N}{e^{\varepsilon/kT}+1}\)
(C)
\(\frac{N}{e^{-\varepsilon/kT}+1}\)
(D)
\(Ne^{-\varepsilon/kT}\)
Check Answer
Option C
Q.No:2 JAM-2015
A rigid and thermally isolated tank is divided into two compartments of equal volume \(V\), separated by a thin membrane. One compartment contains one mole of an ideal gas \(A\) and the other compartment contains one mole of a different ideal gas \(B\). The two gases are in thermal equilibrium at a temperature \(T\). If the membrane ruptures, the two gases mix. Assume that the gases are chemically inert. The change in the total entropy of the gases on mixing is
(A)
\(0\)
(B)
\(R\ln{2}\)
(C)
\(\frac{3}{2}R\ln{2}\)
(D)
\(2R\ln{2}\)
Check Answer
Option D
Q.No:3 JAM-2015
A rigid triangular molecule consists of three non-collinear atoms joined by rigid rods. The constant pressure molar specific heat (\(C_p\)) of an ideal gas consisting of such molecules is
(A)
\(6R\)
(B)
\(5R\)
(C)
\(4R\)
(D)
\(3R\)
Check Answer
Option C
Q.No:4 JAM-2015
As shown in the P-V diagram, AB and CD are two isotherms at temperatures \(T_1\) and \(T_2\), respectively (\(T_1>T_2\)). AC and BD are two reversible adiabats. In this Carnot cycle, which of the following statements are true?
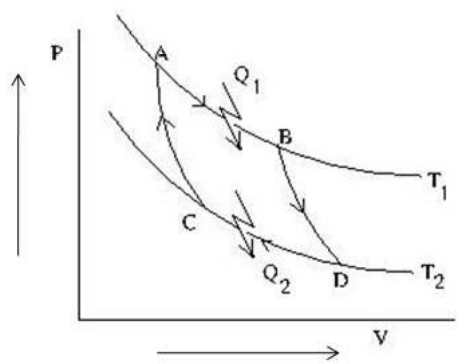
(A)
\(\frac{Q_1}{T_1}=\frac{Q_2}{T_2}\)
(B)
The entropy of the source decreases
(C)
The entropy of the system increases
(D)
Work done by the system \(W=Q_1-Q_2\)
Check Answer
Option A,B,D
Q.No:5 JAM-2015
In the thermodynamic cycle shown in the figure, one mole of a monatomic ideal gas is taken through a cycle. AB is a reversible isothermal expansion at a temperature of \(800 \hspace{1mm}\text{K}\) in which the volume of the gas is doubled. BC is an isobaric contraction to the original volume in which the temperature is reduced to \(300 \hspace{1mm}\text{K}\). CA is a constant volume process in which the pressure and temperature return to their initial values. The net amount of heat (in Joules) absorbed by the gas in one complete cycle is __________.
Check Answer
Ans 445-455
Q.No:6 JAM-2015
One gram of ice at \(0^{\circ}\text{C}\) is melted and heated to water at \(39^{\circ}\text{C}\). Assume that the specific heat remains constant over the entire process. The latent heat of fusion of ice is \(80 \hspace{1mm}\text{Calories}/\text{gm}\). The entropy change in the process (in Calories per degree) is ___________.
Check Answer
Ans 0.4-0.5
Q.No:7 JAM-2016
A spherical closed container with smooth inner wall contains a monoatomic ideal gas. If the collisions between the wall and the atoms are elastic, then the Maxwell speed-distribution function \(\left(\frac{dn_{\nu}}{d\nu}\right)\) for the atoms is best represented by:
Check Answer
Option C
Q.No:8 JAM-2016
For an ideal gas, which one of the following T-S diagrams is valid?
Check Answer
Option A
Q.No:9 JAM-2016
If \(U, F, H\), and \(G\) represent internal energy, Helmholtz free energy, enthalpy, and Gibbs free energy respectively, then which one of the following is a correct thermodynamic relation?
(A)
\(dU=P dV-T dS\)
(B)
\(dH=V dP+T dS\)
(C)
\(dF=-P dV+S dT\)
(D)
\(dG=V dP+S dT\)
Check Answer
Option B
Q.No:10 JAM-2016
One mole of an ideal gas with average molecular speed \(\nu_0\) is kept in a container of fixed volume. If the temperature of the gas is increased such that the average speed gets doubled, then
(A)
the mean free path of the gas molecule will increase.
(B)
the mean free path of the gas molecule will not change.
(C)
the mean free path of the gas molecule will decrease.
(D)
the collision frequency of the gas molecule with wall of the container remains unchanged.
Check Answer
Option B
Q.No:11 JAM-2016
The P-V diagram below shows three possible paths for an ideal gas to reach the final state \(f\) from an initial state \(i\). Which among the following statement(s) is(are) correct?
(A)
The work done by the gas is maximum along path-3.
(B)
Minimum change in the internal energy occurs along path-2.
(C)
Maximum heat transfer is for path-1.
(D)
Heat transfer is path independent.
Check Answer
Option A
Q.No:12 JAM-2016
Potential energy \(U\) as a function of \(r\) is shown below. If a particle of mass \(m_1\) and energy \(E_1\), starting from \(r\gg a\), moves towards the origin, then
(A)
there is only one turning point for the particle.
(B)
velocity of the particle starts to increase at \(r=a\) and reaches its maximum at \(r=c\).
(C)
velocities of the particle at \(r=a\) and \(r=b\) are equal.
(D)
the particle gets bounded if it elastically collides with a stationary particle of mass \(m_2\) at \(r=c\), imparting a momentum greater than \(\sqrt{2m_2 E_1}\).
Check Answer
Option A,B,C or A,B,C,D
Q.No:13 JAM-2016
A cylinder contains \(16\) g of \(O_2\) The work done when the gas is compressed to \(75\%\) of the original volume at constant temperature of \(27^\circ \)C is _______________ J .
\([\)Universal gas constant \(R=8.31 J/\)(mole K)\(]\)
Check Answer
Ans 358-359
Q.No:14 JAM-2016
An aluminum plate of mass 0.1 kg at \(95^\circ\) C is immersed in 0.5 litre of water at \(20^\circ\) C kept inside an insulating container and is then removed. If the temperature of the water is found to be \(23^\circ\) C, then the temperature of the aluminum plate is _____________ \(^\circ C\).
(The specific heat of water and aluminum are 4200 J/kg-K and 900 J/kg-K respectively, the density of water is 1000 kg/\(m^3\))
Check Answer
Ans 24-26
Q.No:15 JAM-2016
If there is a \(10\%\) decrease in the atmospheric pressure at a hill compared to the pressure at sea level, then the change in the boiling point of water is ______________ \(^\circ C\)
(Take latent heat of vaporisation of water as 2270 kJ/kg and the change in the specific volume at the boiling point to be \(1.2 m^3\)/kg.)
Check Answer
Ans 1.9-2.1
Q.No:16 JAM-2017
Consider a system of \(N\) particles obeying classical statistics, each of which can have an energy \(0\) or \(E\) . The system is in thermal contact with a reservoir maintained at a temperature \(T\) .Let \(k\) denote the Boltzmann constant. Which one of the following statements regarding the total energy \(U\) and the heat capacity \(C\) of the system is correct?
(A)
\(U=\frac{NE}{1+e^{E/kT}}\) and \(C=k\frac{NE}{kT}\frac{e^{E/kT}}{(1+e^{E/kT})^2}\)
(B)
\(U=\frac{NE}{kT}\frac{E}{1+e^{E/kT}}\) and \(C=k\frac{NE}{kT}\frac{e^{E/kT}}{(1+e^{-E/kT})^2}\)
(C)
\(U=\frac{NE}{1+e^{E/kT}}\) and \(C=k\frac{NE^2}{(kT)^2}\frac{e^{E/kT}}{(1+e^{E/kT})^2}\)
(D)
\(U=\frac{NE}{1+e^{E/kT}}\) and \(C=k\frac{NE^2}{(kT)^2}\frac{e^{E/kT}}{(1+e^{E/kT})^2}\)
Check Answer
Option C OR D
Q.No:17 JAM-2017
Consider two identical, finite, isolated systems of constant heat capacity \(C\) at temperature \(T_1\) and \(T_2\)\((T_1>T_2)\). An engine works between them until their temperatures become equal. Taking into account that the work performed by the engine will be
maximum \((=W_{max})\) if the process is reversible (equivalently, the entropy change of the entire system is zero), the value of \(W_{max}\) is :
(A)
\(C(T_1-T_2)\)
(B)
\(\frac{C(T_1-T_2)}{2}\)
(C)
\(C(T_1-T_2-\sqrt{T_1T_2})\)
(D)
\(C(\sqrt{T_1}-\sqrt{T_2})^2\)
Check Answer
Option D
Q.No:18 JAM-2017
A white dwarf star has \(V\) and contains \(N\) electrons so that the density of electrons is \(n=\frac{N}{V}\). Taking the temperature of the star to be 0K , the average energy per electron in the star is \(\epsilon_0=\frac{3\hbar^2}{10\hspace{1mm}m}(3\pi^2 n)^{3/2} \),where \(m\) is the mass of the electron. The electronic pressure in the star is:
(A)
\(n\epsilon_0\)
(B)
\(2n\epsilon_0\)
(C)
\(\frac{1}{3}n\epsilon_0\)
(D)
\(\frac{2}{3}n\epsilon_0\)
Check Answer
Option D
Q.No:19 JAM-2017
In the radiation emitted by a black body, the ratio of the spectral densities at frequencies \(2v\) and \(v\) will very with \(v\) as:
(A)
\([e^{hv/k_B T}-1]^{-1}\)
(B)
\([e^{hv/k_B T}+1]^{-1}\)
(C)
\([e^{hv/k_B T}-1]\)
(D)
\([e^{hv/k_B T}+1]\)
Check Answer
Option B
Q.No:20 JAM-2017
An isolated box is divided into two equal compartments by a partition (see figure). One compartment contains a van der Waals gas while the other compartment is empty. The partition between the two compartments is now removed. After the gas has filled the
entire box and equilibrium has been achieved, which of the following statement(s) is (are) correct?
(A)
Internal energy of the gas has not changed
(B)
Internal energy of the gas has decreased
(C)
Temperature of the gas has increased
(D)
Temperature of the gas has decreased
Check Answer
Option A,D
Q.No:21 JAM-2017
Consider a Carnot engine operating between temperature of 600K and 400K . The engine performs 1000 J of work per cycle. The heat (in Joules) extracted per cycle from the high temperature reservoir is _____________.
(Specify your answer to two digits after the decimal point)
Check Answer
Ans 2995-3005
Q.No:22 JAM-2017
Starting with the equation \(TdS=dU+pdV\) and using the appropriate Maxwell’s relation
along with the expression for heat capacity \(C_p\) (see useful information), the derivative \((\frac{\partial p}{\partial T})_S\) for a substance can be expressed in terms of its specific heat \(c_p\), density \(\rho\), coefficient of volume expansion \(\beta\) and temperature \(T\).For ice,\(c_p=2010\)J/kg-K, \(\rho=10^3 kg/m^3\) and \(\beta=1.6\times 10^{-4}/^\circ K\). If the value of \((\frac{\partial p}{\partial T})_S\) at 270K is \(N\times 10^7\)Pa/K, then the value of \(N\) is __________.
(Specify your answer to two digits after the decimal point)
Check Answer
Ans 4.60-4.70
Q.No:23 JAM-2018
Two boxes \(A\) and \(B\) contain an equal number of molecules of the same gas. If the volumes are \(V_A\) and \(V_B\), and \(\lambda_A\) and \(\lambda_B\) denote respective mean free paths, then
(A)
\(\lambda_A =\lambda_B\)
(B)
\(\frac{\lambda_A}{V_A}=\frac{\lambda_B}{V_B}\)
(C)
\(\frac{\lambda_A}{V_A^{1/3}}=\frac{\lambda_B}{V_B^{1/3}}\)
(D)
\(\lambda_A V_A =\lambda_B V_B\)
Check Answer
Option B
Q.No:24 JAM-2018
The equation of state for one mole of a non-ideal gas is given by \(PV=A(1+\frac{B}{V})\), where the coefficients \(A\) and \(B\) are temperature dependent. If the volume changes from \(V_1\) to \(V_2\) in an isothermal process, the work done by the gas is
(A)
\(AB(\frac{1}{V_1}-\frac{1}{V_2})\)
(B)
\(AB\hspace{1mm}ln(\frac{V_1}{V_2})\)
(C)
\(A\hspace{1mm}ln(\frac{V_1}{V_2})+AB(\frac{1}{V_1}-\frac{1}{V_2}) \)
(D)
\(A \hspace{1mm} ln(\frac{V_2-V_1}{V_1})+B\)
Check Answer
Option C
Q.No:25 JAM-2018
An ideal gas consists of three dimensional polyatomic molecules. The temperature is such that only one vibrational mode is excited. If \(R\) denotes the gas constant, then the specific heat at constant volume of one mole of the gas at this temperature is
(A)
\(3R\)
(B)
\(\frac{7}{3}R\)
(C)
\(4R\)
(D)
\(\frac{9}{2}R\)
Check Answer
Option C
Q.No:26 JAM-2018
Consider an ensemble of thermodynamic systems, each of which is characterized by the same number of particles, pressure and temperature. The thermodynamic function describing the ensemble is
(A)
Enthalpy
(B)
Helmholtz free energy
(C)
Gibbs free energy
(D)
Entropy
Check Answer
Option C
Q.No:27 JAM-2018
Which of the following relations is (are) true for thermodynamic variables?
(A)
\(T \hspace{0.5mm}dS=C_VdT+T(\frac{\partial P}{\partial T})_V dV\)
(B)
\(T \hspace{0.5mm}dS=C_PdT-T(\frac{\partial P}{\partial T})_V dV\)
(C)
\(dF=-SdT+PdV\)
(D)
\(dG=-SdT+VdP\)
Check Answer
Option A,B,D
Q.No:28 JAM-2018
Consider a monoatomic ideal gas operating in a closed cycle as shown in the P-V diagram given below. The ratio \(\frac{P_1}{P_2}\) is _____________.
(Specify your answer upto two digits after the decimal point.)
Check Answer
Ans 0.14-0.18
Q.No:29 JAM-2018
Consider the first order phase transition of the sublimation of zinc. Assume the vapor to be an ideal gas and the molar volume of solid to be negligible. Experimentally, it is found that \(lof_{10}(P)=-\frac{C_1}{T}+C_2\), where \(P\) is the vapor pressure in Pascal, \(T\) is in K,\(C_1\) = 6790 K and \(C_2\) = 9. The latentheat of sublimation of zinc from the Clausius -Clapeyron equation is __________ kJ/mole. (\(R\) =8.314 J/mole.K)
(Specify your answer in kJ/mole upto one digit after the decimal point.)
