3D and Angular Momentum CSIR - S. N. Bose Physics Learning Center

Q.No:1 CSIR-Dec-2014

Consider the normalized wavefunction \[ \phi=a_1 \psi_{11}+a_2 \psi_{10}+a_3 \psi_{1-1} \] where \(\psi_{lm}\) is a simultaneous normalized eigenfunction of the angular momentum operators \(L^2\) and \(L_z\), with eigenvalues \(l(l+1)\hbar^2\) and \(m\hbar\) respectively. If \(\phi\) is an eigenfunction of the operator \(L_x\) with eigenvalue \(\hbar\), then

(1) \item \(a_1=-a_3=\frac{1}{2}, a_2=\frac{1}{\sqrt{2}}\)

(2) \(a_1=a_3=\frac{1}{2}, a_2=\frac{1}{\sqrt{2}}\)

(3) \(a_1=a_3=\frac{1}{2}, a_2=-\frac{1}{\sqrt{2}}\)

(4) \(a_1=a_2=a_3=\frac{1}{\sqrt{3}}\)

Check Answer

Option 2

Q.No:2 CSIR-Dec-2014

Let \(\vec{\mathbf{\sigma}}=(\sigma_1, \sigma_2, \sigma_3)\), where \(\sigma_1, \sigma_2, \sigma_3\) ar the Pauli matrices. If \(\vec{\mathbf{a}}\) and \(\vec{\mathbf{b}}\) are two arbitrary constant vectors in three dimensions, the commutator \([\vec{\mathbf{a}}.\vec{\mathbf{\sigma}}, \vec{\mathbf{b}}.\vec{\mathbf{\sigma}}]\) is equal to (in the following \(I\) is the identity matrix)

(1) \((\vec{\mathbf{a}}.\vec{\mathbf{b}})(\sigma_1+\sigma_2+\sigma_3)\)

(2) \(2i(\vec{\mathbf{a}}\times \vec{\mathbf{b}}).\vec{\mathbf{\sigma}}\)

(3) \((\vec{\mathbf{a}}.\vec{\mathbf{b}})I\)

(4) \(|\vec{\mathbf{a}}| |\vec{\mathbf{b}}|I\)

Check Answer

Option 2

Q.No:3 CSIR-June-2015

The ratio of the energy of the first excited state \(E_1\), to that of the ground state \(E_o.\) of a particle in a three-dimensional rectangular box of sides L,L and L/2, is

(1) 3:2

(2) 2:1

(3) 4:1

(4) 4:3

Check Answer

Option 1

Q.No:4 CSIR-June-2015

If \(L_{i}\) are the components of the angular momentum operator \(\overrightarrow{L}\), then the arrow operator \(\sum_{i=1,2,3}\left[\left[\vec{L}, L_{i}\right], L_{i}\right]\) equals

(1) \(\overrightarrow{L}\)

(2) \(2\overrightarrow{L}\)

(3) \(3\overrightarrow{L}\)

(4) \(-\overrightarrow{L}\)

Check Answer

Option 2

Q.No:5 CSIR-Dec-2015

Let \(\psi_{nlm}\) denote the eigenstates of a hydrogen atom in the usual notation. The state \[ \frac{1}{5}[2\psi_{200}-3\psi_{211}+\sqrt{7}\psi_{210}-\sqrt{5}\psi_{21-1}] \] is an eigenstate of

(1) \(L^2\), but not of the Hamiltonian or \(L_z\)

(2) the Hamiltonian, but not of \(L^2\) or \(L_z\)

(3) the Hamiltonian, \(L^2\) and \(L_z\)

(4) \(L^2\) and \(L_z\), but not of the Hamiltonian

Check Answer

Option 2

Q.No:6 CSIR-Dec-2015

The Hamiltonian for a spin-1/2 particle at rest is given by \(H=E_0(\sigma_z+\alpha \sigma_x)\), where \(\sigma_x\) and \(\sigma_z\) are Pauli spin matrices and \(E_0\) and \(\alpha\) are constants. The eigenvalues of this Hamiltonian are

(1) \(\pm E_0\sqrt{1+\alpha^2}\)

(2) \(\pm E_0\sqrt{1-\alpha^2}\)

(3) \(E_0\) (doubly degenerate)

(4) \(E_0\left(1\pm \frac{1}{2}\alpha^2\right)\)

Check Answer

Option 1

Q.No:7 CSIR-Dec-2015

The product of the uncertainties \((\Delta L_x)(\Delta L_y)\) for a particle in the state \(a|1, 1\rangle+b|1, -1\rangle\) (where \(|l, m\rangle\) denotes an eigenstate of \(L^2\) and \(L_z\)) will be a minimum for

(1) \(a=\pm ib\)

(2) \(a=0\) and \(b=1\)

(3) \(a=\frac{\sqrt{3}}{2}\) and \(b=\frac{1}{2}\)

(4) \(a=\pm b\)

Check Answer

Option 4

Q.No:8 CSIR-June-2016

If \(\hat{L}_x, \hat{L}_y\) and \(\hat{L}_z\) are the components of the angular momentum operator in three dimensions, the commutator \([\hat{L}_x, \hat{L}_x \hat{L}_y \hat{L}_z]\) may be simplified to

(1) \(i\hbar L_x(\hat{L}_z^2-\hat{L}_y^2)\)

(2) \(i\hbar \hat{L}_z \hat{L}_y \hat{L}_x\)

(3) \(i\hbar L_x(2\hat{L}_z^2-\hat{L}_y^2)\)

(4) \(i\hbar \hat{L}_z \hat{L}_y \hat{L}_x\)

Check Answer

Option 1

Q.No:9 CSIR-June-2016

Suppose that the Coulomb potential of the hydrogen atom is changed by adding an inverse-square term such that the total potential is \(V(\vec{r})=-\frac{Ze^2}{r}+\frac{g}{r^2}\), where \(g\) is a constant. The energy eigenvalues \(E_{nlm}\) in the modified potential

(1) depend on \(n\) and \(l\), but not on \(m\)

(2) depend on \(n\) but not on \(l\) and \(m\)

(3) depend on \(n\) and \(m\), but not on \(l\)

(4) depend explicitly on all three quantum numbers \(n, l\) and \(m\)

Check Answer

Option 1

Q.No:10 CSIR-June-2017

Let \(\sigma_x, \sigma_y, \sigma_z\) be the Pauli matrices and \(x' \sigma_x+y' \sigma_y+z' \sigma_z=\exp{\left(\frac{i\theta \sigma_z}{2}\right)}\times [x\sigma_x+y\sigma_y+z\sigma_z]\exp{\left(-\frac{i\theta \sigma_z}{2}\right)}\). Then the coordinates are related as follows

(1) \(\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}\cos{\theta}&-\sin{\theta}&0\\\sin{\theta}&\cos{\theta}&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}\)

(2) \(\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}\cos{\theta}&\sin{\theta}&0\\-\sin{\theta}&\cos{\theta}&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}\)

(3) \(\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}\cos{\frac{\theta}{2}}&\sin{\frac{\theta}{2}}&0\\-\sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}\)

(4) \(\begin{pmatrix}x'\\y'\\z'\end{pmatrix}=\begin{pmatrix}\cos{\frac{\theta}{2}}&-\sin{\frac{\theta}{2}}&0\\\sin{\frac{\theta}{2}}&\cos{\frac{\theta}{2}}&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}\)

Check Answer

Option 2

Q.No:11 CSIR-Dec-2017

The normalized wavefunction of a particle in three dimensions is given by \(\psi(r, \theta, \varphi)=\frac{1}{\sqrt{8\pi a^3}}e^{-r/2a}\), where \(a>0\) is a constant. The ratio of the most probable distance from the origin to the mean distance from the origin, is. [You may use \(\int_0^{\infty} dx x^n e^{-x}=n!\).]

(1) \(1/3\)

(2) \(1/2\)

(3) \(3/2\)

(4) \(2/3\)

Check Answer

Option 4

Q.No:12 CSIR-June-2018

A particle of mass \(m\) is confined in a three-dimensional box by the potential \[ V(x, y, z)= \left\{ \begin{array}{ll} 0, & 0\leq x, y, z\leq a, \\ \infty & \text{otherwise}. \end{array} \right. \] The number of eigenstates of Hamiltonian with energy \(\frac{9\hbar^2 \pi^2}{2ma^2}\) is

(1) \(1\)

(2) \(6\)

(3) \(3\)

(4) \(4\)

Check Answer

Option 3

Q.No:13 CSIR-June-2018

The Hamiltonian of a spin-\(\frac{1}{2}\) particle in a magnetic field \(\vec{B}\) is given by \(H=-\mu \vec{B}.\vec{\sigma}\), where \(\mu\) is a real constant and \(\vec{\sigma}=(\sigma_x, \sigma_y, \sigma_z)\) are the Pauli spin matrices. If \(\vec{B}=(B_0, B_0, 0)\) and the spin state at time \(t=0\) is an eigenstate of \(\sigma_x\), then of the expectation values \(\langle \sigma_x\rangle, \langle \sigma_y\rangle\) and \(\langle \sigma_z\rangle\)

(1) only \(\langle \sigma_x\rangle\) changes with time

(2) only \(\langle \sigma_y\rangle\) changes with time

(3) only \(\langle \sigma_z\rangle\) changes with time

(4) all three change with time

Check Answer

Option 4

Q.No:14 CSIR-June-2018

Two Stern-Gerlach apparatus \(S_1\) and \(S_2\) are kept in a line (\(x\)-axis). The directions of their magnetic fields are along the positive \(z\)- and \(y\)-axes, respectively. Each apparatus only transmits particles with spins aligned in the direction of its magnetic field. If an initially unpolarized beam of spin-\(\frac{1}{2}\) particles passes through this configuration, the ratio of intensities \(I_0:I_f\) of the initial and final beams, is

(1) \(16:1\)

(2) \(2:1\)

(3) \(4:1\)

(4) \(1:0\)

Check Answer

Option 3

Q.No:15 CSIR-Dec-2018

The ground state energy of an anisotropic harmonic oscillator described by the potential \(V(x, y, z)=\frac{1}{2}m\omega^2 x^2+2m\omega^2 y^2+8m\omega^2 z^2\) (in units of \(\hbar \omega\)) is

(1) \(5/2\)

(2) \(7/2\)

(3) \(3/2\)

(4) \(1/2\)

Check Answer

Option 2

Q.No:16 CSIR-Dec-2018

Let the wavefunction of the electron in a hydrogen atom be \[ \psi(\vec{r})=\frac{1}{\sqrt{6}}\phi_{200}(\vec{r})+\sqrt{\frac{2}{3}}\phi_{21-1}(\vec{r})-\frac{1}{\sqrt{6}}\phi_{100}(\vec{r}) \] where \(\phi_{nlm}\) are the eigenstates of the Hamiltonian in the standard notation. The expectation value of the energy in this state is

(1) \(-10.8 eV\)

(2) \(-6.2 eV\)

(3) \(-9.5 eV\)

(4) \(-5.1 eV\)

Check Answer

Option 4

Q.No:17 CSIR-Dec-2018

Consider the operator \(A_x=L_y p_z-L_z p_y\), where \(L_i\) and \(p_i\) denote, respectively, the components of the angular momentum and momentum operators. The commutator \([A_x, x]\), where \(x\) is the \(x\)-component of the position operator, is

(1) \(-i\hbar(zp_z+yp_y)\)

(2) \(-i\hbar(zp_z-yp_y)\)

(3) \(i\hbar(zp_z+yp_y)\)

(4) \(i\hbar(zp_z-yp_y)\)

Check Answer

Option 1

Q.No:18 CSIR-Dec-2018

If the position of the electron in the ground state of a Hydrogen atom is measured, the probability that it will be found at a distance \(r\geq a_0\) (\(a_0\) being Bohr radius) is nearest to

(1) \(0.91\)

(2) \(0.66\)

(3) \(0.32\)

(4) \(0.13\)

Check Answer

Option 2

Q.No:19 CSIR-Dec-2018

A system of spin-\(\frac{1}{2}\) particles is prepared to be in the eigenstate of \(\sigma_z\) with eigenvalue \(+1\). The system is rotated by an angle of \(60^{\circ}\) about the \(x\)-axis. After the rotation, the fraction of the particles that will be measured to be in the eigenstate of \(\sigma_z\) with eigenvalue \(+1\) is

(1) \(1/3\)

(2) \(2/3\)

(3) \(1/4\)

(4) \(3/4\)

Check Answer

Option 4

Q.No:20 CSIR-June-2019

A particle moving in a central potential is described by a wavefunction \(\psi(\mathbf{r})=zf(r)\) where \(\mathbf{r}=(x, y, z)\) is the position vector of the particle and \(f(r)\) is a function of \(r=|\mathbf{r}|\). If \(\mathbf{L}\) is the total angular momentum of the particle, the value of \(L^2\) must be

(1) \(2\hbar^2\)

(2) \(\hbar^2\)

(3) \(4\hbar^2\)

(4) \(\frac{3}{4}\hbar^2\)

Check Answer

Option 1

Q.No:21 CSIR-Dec-2019

The normalized wavefunction of a particle in three dimensions is given by \(\psi(x, y, z)=Nz\exp{[-a(x^2+y^2+z^2)]}\) where \(a\) is a positive constant and \(N\) is a normalization constant. If \(\mathbf{L}\) is the angular momentum operator, the eigenvalues of \(\mathbf{L}^2\) and \(L_z\), respectively, are

(1) \(2\hbar^2\) and \(\hbar\)

(2) \(\hbar^2\) and \(0\)

(3) \(2\hbar^2\) and \(0\)

(4) \(\frac{3}{4}\hbar^2\) and \(\frac{1}{2}\hbar\)

Check Answer

Option 3

Q.No:22 CSIR-Dec-2019

The wavefunction of a particle of mass \(m\), constrained to move on a circle of unit radius centered at the origin in the \(xy\)-plane, is described by \(\psi(\phi)=A\cos^2{\phi}\), where \(\phi\) is the aziamuthal angle. All the possible outcomes of measurements of the \(z\)-component of the angular momentum \(L_z\) in this state, in units of \(\hbar\), are

(1) \(\pm 1\) and \(0\)

(2) \(\pm 1\)

(3) \(\pm 2\)

(4) \(\pm 2\) and \(0\)

Check Answer

Option 4

Q.No:23 Assam CSIR-Dec-2019

The Hamiltonian of a spin \(\frac{1}{2}\) particle, precessing in the presence of a magnetic field \(B\) along the positive \(x\)-direction, is \(H=-\mu_B BS_x\), where \(\mu_B\) is the Bohr magneton. At time \(t=0\), the particle is in an eigenstate of \(S_z\) with eigenvalue \(\hbar/2\). The earliest time when it will be in the eigenstate of \(S_y\) with eigenvalue \(\hbar/2\), is

(1) \(\pi/(2\mu_B B)\)

(2) \(\pi/(4\mu_B B)\)

(3) \(3\pi/(2\mu_B B)\)

(4) \(2\pi/(3\mu_B B)\)

Check Answer

Option 1

Q.No:24 CSIR-June-2020

An angular momentum eigenstate \(|j, 0\rangle\) is rotated by an infinitesimally small angle \(\varepsilon\) about the positive \(y\)-axis in the counter clockwise direction. The rotated state, to order \(\varepsilon\) (upto a normalisation constant), is

(a) \(|j, 0\rangle-\frac{\varepsilon}{2}\sqrt{j(j+1)}(|j, 1\rangle+|j, -1\rangle)\)

(b) \(|j, 0\rangle-\frac{\varepsilon}{2}\sqrt{j(j+1)}(|j, 1\rangle-|j, -1\rangle)\)

(d) \(|j, 0\rangle-\frac{\varepsilon}{2}\sqrt{j(j+1)}|j, 1\rangle-\frac{\varepsilon}{2}\sqrt{j(j-1)}|j, -1\rangle\)

Check Answer

Option b

Q.No:25 CSIR-June-2020

The state of an electron in a hydrogen atom is \[ |\psi\rangle=\frac{1}{\sqrt{6}}|1, 0, 0\rangle+\frac{1}{\sqrt{3}}|2, 1, 0\rangle+\frac{1}{\sqrt{2}}|3, 1, -1\rangle \] where \(|n, l, m\rangle\) denotes common eigenstates of \(\hat{H}, \hat{L^2}\) and \(\hat{L_z}\) operators in the standard notation. In a measurement of \(\hat{L}_z\) for the electron in this state, the result is recorded to be \(0\). Subsequently a measurement of energy is performed. The probability that the result is \(E_2\) (the energy of the \(n=2\) state) is

(a) \(1\)

(b) \(1/2\)

(d) \(1/3\)

Check Answer

Option c

Q.No:26 CSIR-Feb-2022

Which of the following two physical quantities cannot be measured simultaneously with arbitrary accuracy for the motion of a quantum particle in three dimensions?

(1) square of the radial position and z -component of angular momentum (\(r^2\) and \(L_z\))

(2) x - components of linear and angular momenta (\(p_x\) and \(L_x\) )

(3) y -component of position and z -component of angular momentum (\(y\) and \(L^2\) )

(4) squares of the magnitudes of the linear and angular momenta (\(p^2\) and \(L^2\) )

Check Answer

Option 3

Q.No:27 CSIR-Sep-2022

Consider the Hamiltonian \(H=AI+B\sigma_x+C\sigma_y\), where \(A,B\) and \(C\) are positive constants, \(I\) is the \(2\times2\) matrix and \(\sigma_x\) and \(\sigma_y\) are Pouli matrices. If the normalized eigenvector corresponding to its largest energy eigenvelue is \(\frac{1}{\sqrt{2}}\begin{pmatrix} 1\\ y \end{pmatrix}\), then \(y\) is

(1) \(\frac{B+iC}{\sqrt{B^2+C^2}}\)

(2) \(\frac{A-iB}{\sqrt{A^2+B^2}}\)

(3) \(\frac{A-iC}{\sqrt{A^2+C^2}}\)

(4) \(\frac{B-iC}{\sqrt{B^2+C^2}}\)

Check Answer

Option 1

Q.No:28 CSIR-Sep-2022

The momentum space representation of the Schrodinger equation of a particle in a potential \(V(\vec{r})\) is \[\left( |\textbf{p}|^2+\beta(\nabla^2 _p)^2 \right) \psi(p,t)=i\hbar \frac{\partial}{\partial t}\psi(p,t)\] where \((\nabla_p)_i=\frac{\partial}{\partial p_i}\), and \(\beta\) is a constant. The potential is (in the following \(V_0\) and \(a\) are constants.)

(1) \(V_0 e^{-r^2/a^2}\)

(2) \(V_0 e^{-r^4/a^4}\)

(3) \(V_0 (\frac{r}{a})^2\)

(4) \(V_0 (\frac{r}{a})^4\)

Check Answer

Option 4

Q.No:29 CSIR-Sep-2022

The Hamiltonian of a spin-1/2 particle in a magnetic field \(B=B_0 \hat{k}\) is given by \(H=\lambda S \cdot B\), where S is its spin (in units of \(\hbar\)) and \(\lambda \) is constant. If the average spin density is \( \langle S \rangle\) for an ensemble of such non-interacting particles, then \(\frac{d}{dt} \langle S_x \rangle \) is

(1) \(\frac{\lambda}{\hbar} B_0 \langle S_x \rangle \)

(2) \(\frac{\lambda}{\hbar} B_0 \langle S_y \rangle \)

(3) \(-\frac{\lambda}{\hbar} B_0 \langle S_x \rangle \)

(4) \(-\frac{\lambda}{\hbar} B_0 \langle S_y \rangle \)

Check Answer

Option 4

Q.No: 30 CSIR-Dec-2023

The Schrödinger wave function for a stationary state of an atom in spherical polar coordinates \((r, \theta, \phi)\) is \[ \psi = A f(r) \sin \theta \cos \theta \, e^{i\phi} \] where \( A \) is the normalization constant. The eigenvalue of \(\hat{L}_z\) for this state is

1) \( 2\hbar \)

2) \( \hbar \)

3) \( -2\hbar \)

4) \( -\hbar \)

Check Answer

Option 2

Q.No: 31 CSIR-Dec-2023

The Hamiltonian for two particles with angular momentum quantum numbers \( l_1 = l_2 = 1 \), is \[ \hat{H} = \frac{\epsilon}{\hbar^2} \left[ (\hat{L}_1 + \hat{L}_2) \cdot \hat{L}_2 - (\hat{L}_{1z} + \hat{L}_{2z})^2 \right]. \] If the operator for the total angular momentum is given by \( \hat{L} = \hat{L}_1 + \hat{L}_2 \), then the possible energy eigenvalues for states with \( l = 2 \), (where the eigenvalues of \( \hat{L}^2 \) are \( l(l + 1)\hbar^2 \)) are

1) \( 3\epsilon, 2\epsilon, -\epsilon \)

2) \( 6\epsilon, 5\epsilon, 2\epsilon \)

3) \( 3\epsilon, 2\epsilon, \epsilon \)

4) \( -3\epsilon, -2\epsilon, \epsilon \)

Check Answer

Option 1

Q.No: 32 CSIR-Dec-2023

The normalized wave function of an electron is \[ \psi(\vec{r}) = R(r) \left[ \sqrt{\frac{3}{8}} Y_1^0(\theta, \phi) \chi_- + \sqrt{\frac{5}{8}} Y_1^1(\theta, \phi) \chi_+ \right], \] where \( Y_l^m \) are the normalized spherical harmonics and \( \chi_{\pm} \) denote the wavefunction for the two spin states with eigenvalues \(\pm\frac{1}{2}\hbar\). The expectation value of the z component of the total angular momentum in the above state is

1) \( -\frac{3}{4}\hbar \)

2) \( -\frac{9}{8}\hbar \)

3) \( \frac{3}{4}\hbar \)

4) \( \frac{9}{8}\hbar \)

Check Answer

Option 3

Q.No: 33 CSIR-Dec-2023

A quantum system is described by the Hamiltonian \[ H = -J\sigma_z + \lambda(t)\sigma_x, \] where \(\sigma_i\) (\(i = x, y, z\)) are Pauli matrices, \(J\) and \(\lambda\) are positive constants (\(J \gg \lambda\)) and \[ \lambda(t) = \begin{cases} 0 & \text{for } t < 0 \\ \lambda & \text{for } 0 < t T \end{cases} \] At \( t < 0 \), the system is in the ground state. The probability of finding the system in the excited state at \( t \gg T \), in the leading order in \(\lambda\) is

1) \( \frac{\lambda^2}{8J^2} \sin^2 \frac{JT}{\hbar} \)

2) \( \frac{\lambda^2}{J^2} \sin^2 \frac{JT}{\hbar} \)

3) \( \frac{\lambda^2}{4J^2} \sin^2 \frac{JT}{\hbar} \)

4) \( \frac{\lambda^2}{16J^2} \sin^2 \frac{JT}{\hbar} \)

Check Answer

Option 2

Q.No: 34 CSIR-June-2023

The Hamiltonian of a two-dimensional quantum harmonic oscillator is \(H=\frac{p_x^2}{2m}+\frac{p_y^2}{2m}+\frac{1}{2}m\omega^2x^2 + 2m\omega^2 y^2\) where \(m\) and \(\omega\) are positive constants. The degeneracy of the energy level \(\frac{27}{2}\hbar\omega\) is

1) 14

2) 13

3) 8

4) 7

Check Answer

Option 4

Q.No: 35 CSIR-JUNE--2023

The radial wavefunction of hydrogen atom with the principal quantum number \(n=2\) and the orbital quantum number \(l=0\) is \(R_{20}=N(1-\frac{r}{2a})e^{-\frac{r}{2a}}\), where \(N\) is the normalization constant. The best schematic representation of the probability density \(P(r)\) for the electron to be between \(r\) and \(r+dr\) is

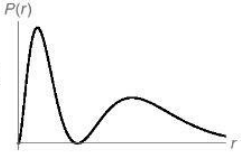
Check Answer

Option 1

Q.No: 36 CSIR-JUNE--2023

Electrons polarized along the \(x\)-direction are in a magnetic field \(B_1\hat{\textbf{i}}+B_2(\hat{\textbf{j}}\cos\hspace{1mm}\omega t+\hat{\textbf{k}}\sin\hspace{1mm}\omega t)\), where \(B_1 >>B_2\) and \(\omega\) are positive constants. The value of \(\hbar\omega\) for which the polarization-flip process is a resonant one, is

1) \(2\mu_B|B_2|\)

2) \(\mu_B|B_1|\)

3) \(\mu_B|B_2|\)

4) \(2\mu_B|B_1|\)

Check Answer

Option 4

Q.No: 37 CSIR-JUNE--2023

1) 0

2) \(4\hbar^{2}\)

3) \(2\hbar^{2}\)

4) \(\hbar^{2}\)

Check Answer

Option 4

Q.No: 38 CSIR-JUNE--2024

If \(\vec{L}\) is the orbital angular momentum operator and \(\vec{\sigma}\) are the Pauli matrices, which of the following operators commutes with \(\vec{\sigma} \cdot \vec{L}\)?

1) \(\vec{L} - \frac{\hbar}{2} \vec{\sigma}\)

2) \(\vec{L} + \frac{\hbar}{2} \vec{\sigma}\)

3) \(\vec{L} + \hbar \vec{\sigma}\)

4) \(\vec{L} - \hbar \vec{\sigma}\)

Check Answer

Option 2

Q.No: 39 CSIR-JUNE--2024

A hydrogen atom is in the state \[ |\psi\rangle = \sqrt{\frac{8}{21}}|\psi_{200}\rangle + \sqrt{\frac{3}{7}}|\psi_{210}\rangle + \sqrt{\frac{4}{21}}|\psi_{311}\rangle, \] where \( |\psi_{nlm}\rangle \) are normalized eigenstates. If \( \hat{L}^2 \) is measured in this state, the probability of obtaining the value \( 2\hbar^2 \) is:

1) \( \frac{13}{21} \)

2) \( \frac{4}{21} \)

3) \( \frac{17}{21} \)

4) \( \frac{3}{7} \)

Check Answer

Option 1

Q.No: 40 CSIR-JUNE--2024

A quantum mechanical system is in the angular momentum state \(|l = 4, l_z = 4|\). The uncertainty in \(L_x\) is

1) \(2\hbar\)

2) 0

3) \(\hbar\sqrt{2}\)

4) \(\hbar\)

Check Answer

Option 3

Q.No: 41 CSIR- Dec-2024

An electron is in the spin state \[ |\psi\rangle = \frac{1}{5} \begin{pmatrix} 3i \\ 4 \end{pmatrix} \] in the \(\hat{S}_{z}\) basis. A measurement of \(\hat{S}_{x}\) is made on this state. The probabilities of getting \(\hbar/2\) and \(-\hbar/2\) are

1) \(\frac{1}{3},\ \frac{2}{3}\)

2) \(\frac{1}{4},\ \frac{3}{4}\)

3) \(\frac{1}{2},\ \frac{1}{2}\)

4) \(\frac{3}{7},\ \frac{4}{7}\)

Check Answer

Option 3

Q.No: 42 CSIR- Dec-2024

Two non–interacting identical spin–\(\frac{1}{2}\) particles, each of mass \(m\), are placed in a two–dimensional infinite square well of side \(L\). The single–particle spatial wavefunction is given by \[ \varphi_{n_{x}, n_{y}}(x, y) = \frac{2}{L} \sin\!\left(\frac{n_{x}\pi x}{L}\right) \sin\!\left(\frac{n_{y}\pi y}{L}\right) \] where \(n_{x}\) and \(n_{y}\) are positive integers. If the particles are in a total spin state \(|j = 1, m = 0\rangle\), the lowest possible energy eigenvalue is

1) \(\frac{5\hbar^{2}\pi^{2}}{2mL^{2}}\)

2) \(\frac{\hbar^{2}\pi^{2}}{mL^{2}}\)

3) \(\frac{2\hbar^{2}\pi^{2}}{mL^{2}}\)

4) \(\frac{7\hbar^{2}\pi^{2}}{2mL^{2}}\)

Check Answer

Option 4

Q.No: 43 CSIR- Dec-2024

A spherical cavity of radius \(r_{0}\) has an impenetrable wall. A quantum particle of mass \(m\) inside the cavity is in its ground state. The pressure exerted on the cavity wall is

1) \(\frac{\pi \hbar^{2}}{4 m r_{0}^{5}}\)

2) \(\frac{\pi \hbar^{2}}{m r_{0}^{5}}\)

3) \(\frac{\pi^{2} \hbar^{2}}{2 m r_{0}^{5}}\)

4) \(\frac{\pi^{2} \hbar^{2}}{4 m r_{0}^{5}}\)

Check Answer

Option 1

Q.No: 44 CSIR- Dec-2024

For a system of two electrons, define an operator \[ \hat{A} = \frac{3}{a^{2}}\,(\hat{S}_{1} \cdot \vec{a})\,(\hat{S}_{2} \cdot \vec{a}) - \hat{S}_{1} \cdot \hat{S}_{2} \] where \(\vec{a}\) is an arbitrary vector, and \(\hat{S}_{1}\) and \(\hat{S}_{2}\) are spin operators. The eigenvalues of \(\hat{A}\) (in units of \(\hbar^{2}\)) are

1) \(-1,\ 1,\ \frac{3}{2},\ \frac{3}{2}\)

2) \(-1,\ -\frac{1}{2},\ -\frac{1}{2},\ 0\)

3) \(\frac{1}{2},\ 1,\ \frac{3}{2},\ \frac{3}{2}\)

4) \(0,\ \frac{1}{2},\ \frac{1}{2},\ -1\)

Check Answer

Option 4

Q.No: 45 CSIR- June-2025

A spin–\(\frac{1}{2}\) system is prepared in the initial state \[ |\varphi\rangle = \frac{\sqrt{3}}{2}\,|+\rangle + \frac{1}{2}\,|-\rangle \] where \(|+\rangle\) and \(|-\rangle\) are eigenstates of \(\hat{S}_{z}\) with eigenvalues \(+\hbar/2\) and \(-\hbar/2\) respectively. A measurement of \(\hat{S}_{z}\) is followed by a measurement of \(\hat{S}_{x}\) on the system. What is the probability that the measurement of \(\hat{S}_{x}\) yields a value \(+\hbar/2\)?

1) \(\frac{1}{2}\)

2) \(\frac{2 + \sqrt{3}}{4}\)

3) \(\frac{2 - \sqrt{3}}{4}\)

4) \(\frac{3}{8}\)