Q.No:1 GATE-2012
Identify the CORRECT statement for the following vectors \(\vec{a}=3\hat{i}+2\hat{j}\) and \(\vec{b}=\hat{i}+2\hat{j}\)
(A) The vectors \(\vec{a}\) and \(\vec{b}\) are linearly independent
(B) The vectors \(\vec{a}\) and \(\vec{b}\) are linearly dependent
(C) The vectors \(\vec{a}\) and \(\vec{b}\) are orthogonal
(D) The vectors \(\vec{a}\) and \(\vec{b}\) are normalized
Check Answer
Option A
Q.No:2 GATE-2012
The eigenvalues of the matrix \(\begin{pmatrix}0&1&0\\1&0&1\\0&1&0\end{pmatrix}\) are
(A)\(0, 1, 1\)
(B) \(0, -\sqrt{2},\sqrt{2}\)
(C) \(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0\)
(D) \(\sqrt{2}, \sqrt{2}, 0\)
Check Answer
Option B
Q.No:3 GATE-2013
The degenerate eigenvalue of the matrix \(\begin{bmatrix}4&-1&-1\\-1&4&-1\\-1&-1&4\end{bmatrix}\) is (your answer should be an integer) _____________
Check Answer
Ans 5
Q.No:4 GATE-2014
The matrix \(A=\frac{1}{\sqrt{3}}\begin{bmatrix}1&1+i\\1-i&-1\end{bmatrix}\) is
(A) orthogonal
(B) symmetric
(C) anti-symmetric
(D) unitary
Check Answer
Option D
Q.No:5 GATE-2014
\(\psi_1\) and \(\psi_2\) are two orthogonal states of a spin \(\frac{1}{2}\) system. It is given that
\[
\psi_1=\frac{1}{\sqrt{3}}\begin{pmatrix}1\\0\end{pmatrix}+\sqrt{\frac{2}{3}}\begin{pmatrix}0\\1\end{pmatrix},
\]
where \(\begin{pmatrix}1\\0\end{pmatrix}\) and \(\begin{pmatrix}0\\1\end{pmatrix}\) represent the spin-up and spin-down states, respectively. When the system is in the state \(\psi_2\), its probability to be in the spin-up state is __________.
Check Answer
Ans 0.66-0.68
Q.No:6 GATE-2016
Which of the following operators is Hermitian?
(A) \(\frac{d}{dx}\)
(B) \(\frac{d^2}{dx^2}\)
(C) \(i\frac{d^2}{dx^2}\)
(D) \(\frac{d^3}{dx^3}\)
Check Answer
Option B
Q.No:7 GATE-2016
If \(x\) and \(p\) are the \(x\) components of the position and the momentum operators of a particle respectively, the commutator \([x^2, p^2]\) is
(A) \(i\hbar(xp+px)\)
(B) \(2i\hbar(xp-px)\)
(C) \(i\hbar(xp+px)\)
(D) \(2i\hbar(xp+px)\)
Check Answer
Option D
Q.No:8 GATE-2016
For the parity operator \(P\), which of the following statements is NOT true?
(A) \(P^{\dagger}=P\)
(B) \(P^2=-P\)
(C) \(P^2=I\)
(D) \(P^{\dagger}=P^{-1}\)
Check Answer
Option B
Q.No:9 GATE-2017
The Poisson bracket \([x, xp_y+yp_x]\) is equal to
(A) \(-x\)
(B) \(y\)
(C) \(2p_x\)
(D) \(p_y\)
Check Answer
Option B
Q.No:10 GATE-2017
Let \(X\) be a column vector of dimension \(n>1\) with at least one non-zero entry. The number of non-zero eigenvalues of the matrix \(M=XX^T\) is
(A) \(0\)
(B) \(n\)
(C) \(1\)
(D) \(n-1\)
Check Answer
Option C
Q.No:11 GATE-2017
Which one of the following operators is Hermitian?
(A) \(i\frac{(p_x x^2-x^2 p_x)}{2}\)
(B) \(i\frac{(p_x x^2+x^2 p_x)}{2}\)
(C) \(e^{ip_x a}\)
(D) \(e^{-ip_x a}\)
Check Answer
Option A
Q.No:12 GATE-2018
The eigenvalues of a Hermitian matrix are all
(A) real
(B) imaginary
(C) of modulus one
(D) real and positive
Check Answer
Option A
Q.No:13 GATE-2018
Given \(\vec{V}_1=\hat{i}-\hat{j}\) and \(\vec{V}_2=-2\hat{i}+3\hat{j}+2\hat{k}\), which one of the following \(\vec{V}_3\) makes \((\vec{V}_1, \vec{V}_2, \vec{V}_3)\) a complete set for a three dimensional real linear vector space?
(A) \(\vec{V}_3=\hat{i}+\hat{j}+4\hat{k}\)
(B) \(\vec{V}_3=2\hat{i}-\hat{j}+2\hat{k}\)
(C) \(\vec{V}_3=\hat{i}+2\hat{j}+6\hat{k}\)
(D) \(\vec{V}_3=2\hat{i}+\hat{j}+4\hat{k}\)
Check Answer
Option D
Q.No:14 GATE-2018
If \(H\) is the Hamiltonian for a free particle with mass \(m\), the commutator \([x, [x, H]]\) is
(A) \(\hbar^2/m\)
(B) \(-\hbar^2/m\)
(C) \(-\hbar^2/(2m)\)
(D) \(\hbar^2/(2m)\)
Check Answer
Option B
Q.No:15 GATE-2019
During a rotation, vectors along the axis of rotation remain unchanged. For the rotation matrix \(\begin{pmatrix}0&1&0\\0&0&-1\\-1&0&0\end{pmatrix}\), the unit vector along the axis of rotation is
(A) \(\frac{1}{3}(2\hat{i}-\hat{j}+2\hat{k})\)
(B) \(\frac{1}{\sqrt{3}}(\hat{i}+\hat{j}-\hat{k})\)
(C) \(\frac{1}{\sqrt{3}}(\hat{i}-\hat{j}-\hat{k})\)
(D) \(\frac{1}{3}(2\hat{i}+2\hat{j}-\hat{k})\)
Check Answer
Option B
Q.No:16 GATE-2019
Let \(|\psi_1\rangle=\begin{pmatrix}1\\0\end{pmatrix}, |\psi_2\rangle=\begin{pmatrix}0\\1\end{pmatrix}\) represent two possible states of a two-level quantum system. The state obtained by the incoherent superposition of \(|\psi_1\rangle\) and \(|\psi_2\rangle\) is given by a density matrix that is defined as \(\rho\equiv c_1|\psi_1\rangle \langle \psi_1|+c_2|\psi_2\rangle \langle \psi_2|\). If \(c_1=0.4\) and \(c_2=0.6\), the matrix element \(\rho_{22}\) (rounded off to one decimal place) is __________.
Check Answer
Ans 0.6
Q.No:17 GATE-2019
The Hamiltonian operator for a two-level quantum system is \(H=\begin{pmatrix}E_1&0\\0&E_2\end{pmatrix}\). If the state of the system at \(t=0\) is given by \(|\psi(0)\rangle=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix}\) then \(|\langle \psi(0)|\psi(t)\rangle|^2\) at a later time \(t\) is
(A) \( \frac{1}{2}\left(1 + e^{-(E_1 - E_2)t/\hbar}\right) \)
(B) \(\frac{1}{2}(1-e^{-(E_1-E_2)t/\hbar})\)
(C) \(\frac{1}{2}(1+\cos{[(E_1-E_2)t/\hbar]})\)
(D) \(\frac{1}{2}(1-\cos{[(E_1-E_2)t/\hbar]})\)
Check Answer
Option C
Q.No:18 GATE-2020
A real, invertible \(3\times 3\) matrix \(M\) has eigenvalues \(\lambda_i\), (\(i=1, 2, 3\)) and the corresponding eigenvectors are \(|e_i\rangle\), (\(i=1, 2, 3\)) respectively. Which one of the following is correct?
(A) \(M|e_i\rangle=\frac{1}{\lambda_i}|e_i\rangle\), for \(i=1, 2, 3\)
(B) \(M^{-1}|e_i\rangle=\frac{1}{\lambda_i}|e_i\rangle\), for \(i=1, 2, 3\)
(C) \(M^{-1}|e_i\rangle=\lambda_i|e_i\rangle\), for \(i=1, 2, 3\)
(D) The eigenvalues of \(M\) and \(M^{-1}\) are not related.
Check Answer
Option B
Q.No:19 GATE-2020
The product of eigenvalues of \(\begin{pmatrix}0&0&1\\0&1&0\\1&0&0\end{pmatrix}\) is
(A) \(-1\)
(B) \(1\)
(C) \(0\)
(D) \(2\)
Check Answer
Option A
Q.No:20 GATE-2020
Let \(|e_1\rangle\equiv\begin{pmatrix}1\\0\\0\end{pmatrix}, |e_2\rangle\equiv\begin{pmatrix}1\\1\\0\end{pmatrix}\) and \(|e_3\rangle\equiv\begin{pmatrix}1\\1\\1\end{pmatrix}\). Let \(S=\{|e_1\rangle, |e_2\rangle, |e_3\rangle\}\). Let \(\mathbb{R}^3\) denote the three-dimensional real vector space. Which one of the following is correct?
(A) \(S\) is an orthonormal set
(B) \(S\) is a linearly dependent set
(C) \(S\) is a basis for \(\mathbb{R}^3\)
(D) \(\sum_{i=1}^{3} |e_i\rangle \langle e_i|=\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}\)
Check Answer
Option C
Q.No:21 GATE-2020
Which one of the following matrices does NOT represent a proper rotation in a plane?
(A) \(\begin{pmatrix}-\sin{\theta}&\cos{\theta}\\-\cos{\theta}&-\sin{\theta}\end{pmatrix}\)
(B) \(\begin{pmatrix}\cos{\theta}&\sin{\theta}\\-\sin{\theta}&\cos{\theta}\end{pmatrix}\)
(C) \(\begin{pmatrix}\sin{\theta}&\cos{\theta}\\-\cos{\theta}&\sin{\theta}\end{pmatrix}\)
(D) \(\begin{pmatrix}-\sin{\theta}&\cos{\theta}\\-\cos{\theta}&\sin{\theta}\end{pmatrix}\)
Check Answer
Option D
Q.No:22 GATE-2021
\(P\) and \(Q\) are two Hermitian matrices and there exists a matrix \(R\), which diagonalizes both of them, such that \(RPR^{-1}=S_1\) and \(RQR^{-1}=S_2\), where \(S_1\) and \(S_2\) are diagonal matrices. The correct statement(s) is(are)
(A) All the elements of both matrices \(S_1\) and \(S_2\) are real.
(B) The matrix \(PQ\) can have complex eigenvalues.
(C) The matrix \(QP\) can have complex eigenvalues.
(D) The matrices \(P\) and \(Q\) commute.
Check Answer
Option A & D
Q.No:23 GATE-2022
An electromagnetic pulse has a pulse width of \(10^{-3}\hspace{1mm}\text{s}\). The uncertainty in the momentum of the corresponding photon is of the order of \(10^{-N} \hspace{1mm}\text{kg}\hspace{1mm}\text{m}\hspace{1mm}\text{s}^{-1}\), where \(N\) is an integer. The value of \(N\) is -------------- (speed of light \(=3\times 10^8 \hspace{1mm}\text{m}\hspace{1mm}\text{s}^{-1}\), \(h=6.6\times 10^{-34} \hspace{1mm}\text{J}\hspace{1mm}\text{s}\))
Check Answer
ANS 39-40
Q.No:24 GATE-2022
What is the maximum number of free independent real parameters specifying an \(n\)-dimensional orthogonal matrix?
(a) \(n(n-2)\)
(b) \((n-1)^2\)
(c) \(\frac{n(n-1)}{2}\)
(d) \(\frac{n(n+1)}{2}\)
Check Answer
Option c
Q.No:25 GATE-2023
A \(4 \times 4\) matrix M has the property \(M^\dagger=-M\) and \(M^4=1\), where \(1\) is the \(4 \times 4\) identity matrix. Which one of the following is the CORRECT set of eigenvalues of the matrix \(M\)?
(A) \((1, 1, -1, -1)\)
(B) \((i, i, -i, -i)\)
(C) \((i, i, i, -i)\)
(D) \((1, 1, -i, -i)\)
Check Answer
Option B
Q.No:26 GATE-2023
Which of the following options represent(s) linearly independent pair(s) of functions of a real variable \(x\) ?
(A) \(e^{ix}\) and \(e^{-ix}\)
(B) \(x\) and \(e^x\)
(C) \(2^x\) and \(2^{-3+x}\)
(D) \(e^{ix}\) and \(sin \hspace{0.5mm} x\)
Check Answer
Option A, B, D
Q.No:27 GATE-2023
The wavefunction of a particle in one dimension is given by
\[\psi(x)=\left\{
\begin{array}{ll}
M & -a<x<a \\
0 & \text{otherwise. }
\end{array}
\right.\]
Here \(M\) and \(a\) are positive constants. If \(\varphi(p)\) is the corresponding momentum space wavefunction, which one of the following plots best represents \(|\varphi(p)|^2\) ?

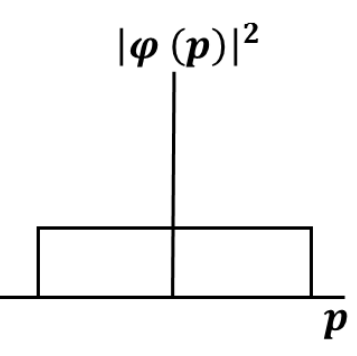
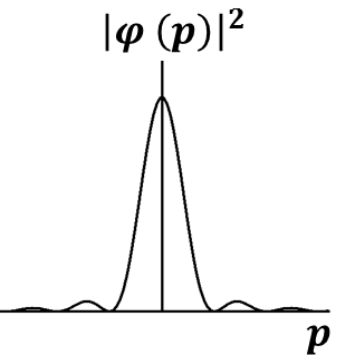

Check Answer
Option C
Q.No:28 GATE-2024
Consider two matrices: \( P = \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix} \) and \( Q = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \). Which of the following statement is/are true?
A) \(P\) and \(Q\) have the same set of eigenvalues
B) \(P\) and \(Q\) commute with each other
C) \(P\) and \(Q\) have different sets of linearly independent eigenvectors
D) \(P\) is diagonalizable
Check Answer
A, B and C
Q.No:29 GATE-2025
Consider the set \(\{1, x, x^{2}\}\). An orthonormal basis in \(x \in [-1,1]\) is formed from these three terms, where the normalization of a function \(f(x)\) is defined via
\[
\int_{-1}^{1} x^{2}\, [f(x)]^{2}\, dx = 1
\]
If the orthonormal basis set is
\[
\left(
\sqrt{\frac{3}{2}},\;
\sqrt{\frac{5}{2}}\, x,\;
\frac{1}{2}\sqrt{\frac{21}{N}}\, (5x^{2} - 3)
\right)
\]
then the value of \(N\) (in integer) is _____

Q.No.1 Discussion :
option(1)
Q.No.2 Discussion :
Answer: B
Q.No.3 Discussion :
Q.No.4 Discussion :
ans
answer
Q.No.5 Discussion :
ans
Q.No.6 Discussion :
Q No6
Q.No.7 Discussion :
Q.No.8 Discussion :
Q.No.9 Discussion :
GATE Qn. 09
Q.No.10 Discussion :
Answer
Q.No.11 Discussion :
Q.No.12 Discussion :
Q.No.13 Discussion :
Q13 GATE
Q.No.14 Discussion :
Q14 GATE
Q.No.15 Discussion :
Q 15
Q.No.16 Discussion :
Solution
Q.No.17 Discussion :
Q.No.18 Discussion :
option B
Q.No.19 Discussion :
Q.No 19 GATE 2020
Option A
Q.No.20 Discussion :
Q.No.21 Discussion :
answer
Q.No.22 Discussion :
Answer (a) and (d)
Q.No.23 Discussion :
Q no 23
Q.No.24 Discussion :
Q.No.25 Discussion :
Q no 25
Q.No.26 Discussion :
A,B,D
Q.No.27 Discussion :
Answer
Q.No.28 Discussion :