Q.No:1 JEST-2012
The net charge of an \(n\)-type semiconductor is
(a)
positive
(b)
zero
(c)
negative
(d)
dependent on the dopant density
Check Answer
Option b
Q.No:2 JEST-2014
When two different solids are brought in contact with each other, which one of the following is true?
(a)
Their Fermi energies become equal
(b)
Their band gaps become equal
(c)
Their chemical potentials become equal
(d)
Their work functions become equal
Check Answer
Option c
Q.No:3 JEST-2015
Given the tight binding dispersion relation \(E(k)=E_0+A\sin^2{\left(\frac{ka}{2}\right)}\), where \(E_0\) and \(A\) are constants and \(a\) is the lattice parameter. What is the group velocity of an electron at the second Brillouin zone boundary?
(a)
\(0\)
(b)
\(\frac{a}{h}\)
(c)
\(\frac{2a}{h}\)
(d)
\(\frac{a}{2h}\)
Check Answer
Option a
Q.No:4 JEST-2020
A carbon rod of resistance \(R_c\) and a metal rod of resistance \(R_m\) are connected in series. Let their linear temperature coefficients of resistivity have magnitudes \(\alpha_c\) and \(\alpha_m\), respectively. The condition that the net resistance would be independent of temperature is
(A)
\(R_c=R_m\)
(B)
\(\alpha_c=\alpha_m\)
(C)
\(R_c/R_m=\alpha_m/\alpha_c\)
(D)
\(R_m/R_c=\alpha_m/\alpha_c\)
Check Answer
Option C
Q.No:5 JEST-2022
Optical excitation of intrinsic germanium creates an average density of \(10^{12}\) conduction electrons per \(cm^3\) in the material at liquid nitrogen temperature. At this temperature, the electron and hole mobilities are equal, \(\mu=0.5\times 10^4 m^2 V^{-2} s^{-1}\). The germanium dielectric constant is \(20\). If \(100\) Volts is applied across \(1 cm\) cube of crystal under these condition, about how much current, in mA, is observed? [Charge of electron \(= 1.6 \times 10^{-19} C\)]
Check Answer
Ans 0.08
Q.No:6 JEST-2023
A silicon crystal sample has 50 billion silicon atoms and 5 million free electrons. The silicon crystal is additionally doped with 5 million pentavalent atoms. Assume that the ambient thermal energy is much smaller than the bandgap of silicon. How many free electrons and holes are there
inside the silicon crystal?
(a) Number of electrons is 30 million and number of holes is zero.
(b) Number of electrons is 10 million and number of holes is zero.
(c) Number of electrons is 10 million and number of holes is 5 million.
(d) Number of electrons is 5 million and number of holes is 5 million.
Check Answer
option b
Q.No:7 JEST-2024
Where does the Fermi level of an n-type semiconductor lie?
(a) Near the conduction band minimum.
(b) Near the valence band maximum.
(c) At the middle of the energy gap.
(d) Inside the valence band.
Check Answer
option a
Q.No: 8 JEST-2024
In an intrinsic semiconductor at \( 300 \, \text{K} \), the number density of electrons is \( n_e = 2.5 \times 10^{20} \, \text{m}^{-3} \). If the mobility of electrons is \( \mu_e = 0.4 \, \text{m}^2\text{V}^{-1}\text{s}^{-1} \) and the mobility of holes is \( \mu_h = 0.2 \, \text{m}^2\text{V}^{-1}\text{s}^{-1} \), find the conductivity in units of mho/m. Charge of a proton \( e = 1.6 \times 10^{-19} \, \text{Coulomb} \).
Check Answer
Ans 24
Q.No:1 TIFR-2012
Suppose the energy band diagram of a certain pure crystalline solid is as shown in the figure below, where the energy (\(E\)) varies with crystal momentum (\(k\)) as \(E\propto k^2\).

At finite temperatures the bottom of the conduction band (CB) is partially filled with electrons (\(e\)) and the top of the valence band (VB) is partially filled with holes (\(h\)). If an electric field is applied to this solid, both \(e\) and \(h\) will start moving. If the time between collisions is the same for both \(e\) and \(h\), then
(a)
\(e\) and \(h\) will move with the same speed in opposite directions
(b)
\(h\) will on an average achieve higher speed than \(e\)
(c)
\(e\) will on an average achieve higher speed than \(h\)
(d)
\(e\) and \(h\) will recombine and after a while there will be no flow of charges
Check Answer
Option b
Q.No:2 TIFR-2013
Consider two energies of a free electron gas in a metal at an absolute temperature \(T\), viz.,
\[
E_{\pm}=E_F\pm \Delta
\]
where \(E_F\) is the Fermi level. If the corresponding electron populations \(n(E_{\pm})\) satisfy the relation \(n(E_{-})/n(E_{+})=2\), then \(\Delta=\)
(a)
\(k_B T\ln{2}\)
(b)
\(2k_B T\)
(c)
\(k_B T/2\)
(d)
\(k_B T\)
Check Answer
Option a
Q.No:3 TIFR-2014
In a low temperature experiment, the resistance of a sensor is used as a thermometer. In order to have better sensitivity in the range \(100 mK\) to \(1.0 K\), which material would make the best sensor?
(a)
insulator
(b)
p-n junction
(c)
pure semiconductor
(d)
metal
Check Answer
Option c
Q.No:4 TIFR-2014
For a pure germanium semiconductor cooled in liquid nitrogen, the average density of conduction electrons is about \(n=10^{12}\) per \(cm^3\). At this temperature the electron and hole mobilities are equal and have the common value \(\mu=5.0\times 10^3 cm^3 V^{-1} s^{-1}\). If a potential of \(100 V\) is applied across a \(1 cm\) cube of this cooled germanium sample, the current observed can be estimated as
(a)
\(80 \mu A\)
(b)
\(160 mA\)
(c)
\(16 mA\)
(d)
\(16 A\)
Check Answer
Option b
Q.No:5 TIFR-2015
An electron makes a transition from the valence band to the conduction band in an indirect band gap semiconductor. Which of the following is NOT true?
(a)
The energy of the electron increases.
(b)
A phonon is involved in the process.
(c)
A photon is absorbed in the process.
(d)
There is no momentum change in the electron.
Check Answer
Option d
Q.No:6 TIFR-2015
Which of the following is the best technique for measuring the effective mass of an electron in a semiconductor?
(a)
Resistivity measurements
(b)
X-ray diffraction experiment
(c)
Cyclotron resonance
(d)
Millikan's oil drop experiment
Check Answer
Option c
Q.No:7 TIFR-2015
In the basic band structure theory of crystalline solids, which of the following leads to energy gaps in the allowed electronic energy values?
(a)
Electron spin
(b)
Bragg reflection
(c)
Electron-electron interaction
(d)
Electron-phonon interaction
Check Answer
Option b
Q.No:8 TIFR-2015
The material inside a box is either a metal or a semiconductor. If \(R\) (\(=1 \Omega\)) is the resistance of the material, which of the following experiments \(\underline{CANNOT}\) distinguish whether it is a metal or a semiconductor?
(a)
Measurement of \(R\) using power supplies of different frequencies.
(b)
Measurement of absorption spectrum in the energy range \(0.1\)--\(2 eV\).
(c)
Measurement of \(R\) at different temperatures.
(d)
Measurement of \(R\) in the presence of different magnetic fields.
Check Answer
Option a
Q.No:9 TIFR-2016
The lattice constant of a material is of the order of a \(\mu m\), and its bond energies are of the order of an eV. The bulk modulus of such a material, in Pascals, is of the order of
(a)
\(10^{-1}\)
(b)
\(10^{-3}\)
(c)
\(10^{-6}\)
(d)
\(10^{9}\)
Check Answer
Option a
Q.No:10 TIFR-2016
The dispersion relation for electrons in the conduction band of a \(n\)-type semiconductor has the form \(E(k)=ak^2+b\) where \(a\) and \(b\) are constants. It was observed that the cyclotron resonance frequency of such electrons is \(\omega_0=1.8\times 10^{11} rad s^{-1}\), when placed in a magnetic field \(B=0.1 W m^{-2}\). It follows that the constant \(a\) must be about
(a)
\(10^{-36}\)
(b)
\(10^{-28}\)
(c)
\(10^{-32}\)
(d)
\(10^{-38}\)
Check Answer
Option d
Q.No:11 TIFR-2017
Consider a \(2\)-D square lattice. The ratio of the kinetic energy of a free electron at a corner of the first Brillouin zone (\(E_c\)) to that of an electron at the midpoint of a side face of the same zone (\(E_m\)) is \(E_c/E_m=\)
(a)
\(1/2\)
(b)
\(2\)
(c)
\(\sqrt{2}\)
(d)
\(1\)
Check Answer
Option b
Q.No:12 TIFR-2020
A semiconductor with donor impurities can be thought in terms of a filled valence band, a filled donor level and an empty valence band at \(T=0\), as shown in the figure below.
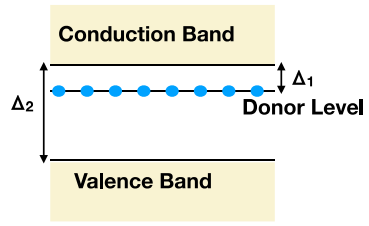
If the band gap between donor level and conduction band is \(\Delta_1\) and that between conduction and valence band is \(\Delta_2\) where \(\Delta_2\gg \Delta_1\), which of the following figures depict the qualitative features of the resistance (\(R\))-vs-temperature (\(T\)) graph of the semi-conductor?
Assume temperature-independent scattering rates and a flat density of states for the bands.
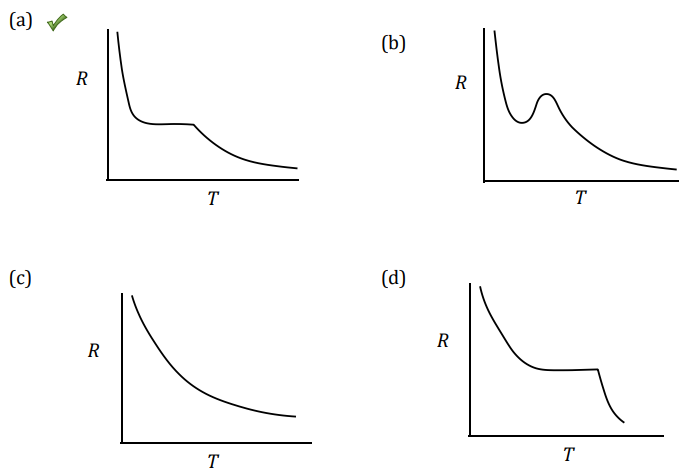
Check Answer
Option a
Q.No:13 TIFR-2021
For a pure germanium semiconductor, cooled in liquid nitrogen, the average density of conduction electrons is about \(n=10^{12} \hspace{1mm}\text{cm}^{-3}\). At this temperature, the electron and hole mobilities are equal and have the common value \(\mu=5.0\times 10^3 \hspace{1mm}\text{cm}^2\text{V}^{-1}\text{s}^{-1}\).
If a potential of \(100 \hspace{1mm}\text{V}\) is applied across opposite faces of a cube of this cooled germanium sample having side \(1 \hspace{1mm}\text{cm}\), the current through the sample can be estimated as
(a)
\(160 \hspace{1mm}\text{mA}\)
(b)
\(16 \hspace{1mm}\text{mA}\)
(c)
\(8 \hspace{1mm}\text{mA}\)
(d)
\(80 \hspace{1mm}\text{mA}\)
Check Answer
Option a
Q.No:14 TIFR-2022
The free electron model of metals (Drude model) explains several physical properties, but cannot be used to explain
(a)
positive value of Hall coefficient
(b)
magnetic susceptibility of the metal
(c)
electrical conductivity of the metal
(d)
thermal conductivity of the metal
Check Answer
Option a
Q.No:15 TIFR-2022
At very low temperatures, the electrical resistivity of most metals is dominated by
(a)
collisions of conduction electrons with impurity atoms and lattice vacancies.
(b)
absorption of conduction electrons by ions in the lattice
(c)
collisions of conduction electrons with lattice phonons.
(d)
transfer of conduction electrons to the valence band.
Check Answer
Option a
Q.No:16 TIFR-2023
An X-ray of wavelength \(\lambda\), when incident on the (101) plane of a cubic lattice with lattice constant \(a\) produces a first-order Bragg’s reflection at \(\theta=30^ \circ\) (\(\theta\) is measured
from the lattice plane).
Suppose this cubic lattice is compressed along the z axis such that its lattice parameters along the x and y axes remain the same while that along the z axis becomes \(\frac{1}{\sqrt{3}}a\) (see figure).
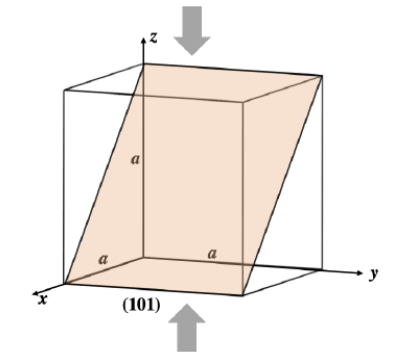
The first-order reflection for the (101) plane of the compressed lattice occurs at:
(a)
\(\theta=45^ \circ\)
(b)
\(\theta=15^ \circ\)
(c)
\(\theta=30^ \circ\)
(d)
\(\theta=60^ \circ\)
Check Answer
Option a
Q.No:17 TIFR-2024
A student designed a new semiconductor with lattice constant \( a \) that crystallizes in the face-centered cubic (fcc) structure. The conduction band minimum of this semiconductor lies at all momentum points equivalent to \( \vec{k} = (0.5, 0, 0) \frac{2\pi}{a} \). How many conduction band minimum points are inside the first Brillouin zone?
(a) 6
(b) 4
(c) 3
(d) 1
Check Answer
Option a
Q.No:18 TIFR-2024
The energy dispersion in the conduction band of a one-dimensional metal with lattice spacing \( a \) is given by,
\[
E(k) = E_0(1 - \cos ka)
\]
where \( k \in [-\pi/a, +\pi/a] \). Suppose that each site contributes one conduction electron to the conduction band. What is the Fermi energy of the system?
(a) \( E_0 \)
(b) \( \frac{E_0}{2} \)
(c) \( 2E_0 \)
(d) \( \frac{E_0}{4} \)
Check Answer
Option a
Q.No:19 TIFR-2025
A student designed a new semiconductor with lattice constant \(a\) that crystallizes
in the face-centered cubic (fcc) structure.
The conduction band minimum of this semiconductor lies at all momentum points
equivalent to
\[
\vec k = (0.5,\,0,\,0)\,\frac{\pi}{a}.
\]
How many conduction band minimum points are inside the first Brillouin zone?
a) 6
b) 4
c) 3
d) 1
Check Answer
Option a
Q.No:20 TIFR-2025
The energy dispersion in the conduction band of a one-dimensional metal with lattice
spacing \(a\) is given by
\[
E(k) = E_0(1 - \cos ka),
\]
where \(k \in (-\pi/a,\,+\pi/a]\).
Suppose that each site contributes one conduction electron to the conduction band.
What is the Fermi energy of the system?
a) \(E_0\)
b) \(\frac{E_0}{2}\)
c) \(2E_0\)
d) \(\frac{E_0}{4}\)
