Q.No:1 JEST-2012
The ground state (apart from normalization) of a particle of unit mass moving in a one-dimensional potential \(V(x)\) is \(\exp{(-x^2/2)}\cosh{(\sqrt{2}x)}\). The potential \(V(x)\), in suitable units so that \(\hbar=1\), is (up to an additive constant)
(b) \(x^2/2-\sqrt{2}x\tanh{(\sqrt{2}x)}\)
(c) \(x^2/2-\sqrt{2}x\tan{(\sqrt{2}x)}\)
(d) \(x^2/2-\sqrt{2}x\coth{(\sqrt{2}x)}\)
Check Answer
Option b
Q.No:2 JEST-2012
The quantum state \(\sin{x}|\uparrow\rangle+\exp{(i\phi)}\cos{x}|\downarrow\rangle\), where \(\langle \uparrow|\downarrow\rangle=0\) and \(x, \phi\) are real, is orthogonal to:
(a) \(\sin{x}|\uparrow\rangle\)
(c) \(\cos{x}|\uparrow\rangle+\exp{(i\phi)}\sin{x}|\downarrow\rangle\)
(c) \(-\cos{x}|\uparrow\rangle-\exp{(i\phi)}\sin{x}|\downarrow\rangle\)
(d) \(-\exp{(-i\phi)}\cos{x}|\uparrow\rangle+\sin{x}|\downarrow\rangle\)
Check Answer
Option d
Q.No:3 JEST-2013
A quantum mechanical particle in a harmonic oscillator potential has the initial wavefunction \(\psi_0(x)+\psi_1(x)\), where \(\psi_0\) and \(\psi_1\) are the real wavefunctions in the ground and first excited states of the harmonic oscillator Hamiltonian. For convenience we take \(m=\hbar=\omega=1\) for the oscillator. What is the probability density of finding the particle at \(x\) at time \(t=\pi\)?
(a) \((\psi_1(x))^2-(\psi_0(x))^2\)
(b) \((\psi_1(x)-\psi_0(x))^2\)
(c) \((\psi_1(x)+\psi_0(x))^2\)
(d) \((\psi_1(x))^2+(\psi_0(x))^2\)
Check Answer
Option b
Q.No:4 JEST-2013
A particle of mass \(m\) is contained in a one-dimensional infinite well extending from \(x=-L/2\) to \(x=L/2\). The particle is in its ground state given by \(\psi_0(x)=\sqrt{2/L}\cos{(\pi x/L)}\). The walls of the box are moved suddenly to form a box extending from \(x=-L\) to \(x=L\). What is the probability that the particle will be in the ground state after this sudden expansion?
(a) \((8/3\pi)^2\)
(b) \(0\)
(c) \((16/3\pi)^2\)
(d) \((4/3\pi)^2\)
Check Answer
Option a
Q.No:5 JEST-2013
If the distribution function of \(x\) is \(f(x)=xe^{-x/\lambda}\) over the interval \(0<x<\infty\), the mean value of \(x\) is
(a) \(\lambda\)
(b) \(2\lambda\)
(c) \(\lambda/2\)
(d) \(0\)
Check Answer
Option b
Q.No:6 JEST-2014
The temperature of a thin bulb filament (assuming that the resistance of the filament is nearly constant) of radius \(r\) and length \(L\) is proportional to
(a) \(r^{1/4} L^{-1/2}\)
(b) \(L^2 r\)
(c) \(L^{1/4} r^{-1}\)
(d) \(r^2 L^{-1}\)
Check Answer
Option a
Q.No:7 JEST-2014
A ball bounces off earth. You are asked to solve this quantum mechanically assuming the earth is an infinitely hard sphere. Consider surface of earth as the origin implying \(V(0)=\propto\) and a linear potential elsewhere (i.e. \(V(x)= mgx\) for \(x>0\)). Which of the following wave functions is physically admissible for this problem (with \(k>0\)):
(a) \(\psi=e^{-kx}/x\)
(b) \(\psi=xe^{-kx^2}\)
(c) \(\psi=-Axe^{kx}\)
(d) \(\psi=Ae^{-kx^2}\)
Check Answer
Option b
Q.No:8 JEST-2015
A particle of mass \(m\) moves in \(1\)-dimensional potential \(V(x)\) which vanishes at infinity. The exact ground state eigenfunction is \(\psi(x)=A\) sech \((\lambda x)\) where \(A\) and \(\lambda\) are constants. The ground state energy eigenvalue of this system is,
(a) \(E=\frac{\hbar^2 \lambda^2}{m}\)
(b) \(E=-\frac{\hbar^2 \lambda^2}{m}\)
(c) \(E=-\frac{\hbar^2 \lambda^2}{2m}\)
(d) \(E=\frac{\hbar^2 \lambda^2}{2m}\)
Check Answer
Option c
Q.No:9 JEST-2015
Given that \(\psi_1\) and \(\psi_2\) are eigenstates of a Hamiltonian with eigenvalues \(E_1\) and \(E_2\) respectively, what is the energy uncertainty in the state \((\psi_1+\psi_2)\)?
(a) \(-\sqrt{E_1 E_2}\)
(b) \(\frac{1}{2}|E_1-E_2|\)
(c) \(\frac{1}{2}(E_1+E_2)\)
(d) \(\frac{1}{\sqrt{2}}|E_2-E_1|\)
Check Answer
Option b
Q.No:10 JEST-2015
The blackbody at a temperature of \(6000 K\) emits a radiation whose intensity spectrum peaks at \(600 nm\). If the temperature is reduced to \(300 K\), the spectrum will peak at,
(a) \(120 \mu m\)
(a) \(12 \mu m\)
(c) \(12 mm\)
(d) \(120 mm\)
Check Answer
Option b
Q.No:11 JEST-2016
An electron confined within a thin layer of semiconductor may be treated as a free particle inside an infinitely deep one-dimensional potential well. If the difference in energies between the first and the second energy levels is \(\delta E\), then the thickness of the layer is:
(a) \(\sqrt{\frac{3\hbar^2 \pi^2}{2m\delta E}}\)
(b) \(\sqrt{\frac{2\hbar^2 \pi^2}{3m\delta E}}\)
(c) \(\sqrt{\frac{\hbar^2 \pi^2}{2m\delta E}}\)
(d) \(\sqrt{\frac{\hbar^2 \pi^2}{m\delta E}}\)
Check Answer
Option a
Q.No:12 JEST-2016
The mean value of random variable \(x\) with probability density \(p(x)=\frac{1}{\sigma \sqrt{2\pi}}\exp{[-(x^2+\mu x)/(2\sigma^2)]}\), is:
(a) \(0\)
(b) \(\mu/2\)
(c) \(-\mu/2\)
(d) \(\sigma\)
Check Answer
Option c
Q.No:13 JEST-2017
If the ground state wavefunction of a particle moving in a one dimensional potential is proportional to \(\exp{(-x^2/2)}\cosh{(\sqrt{2}x)}\), then the potential in suitable units such that \(\hbar=1\), is proportional to
(a) \(x^2\).
(b) \(x^2-2\sqrt{2}x\tanh{(\sqrt{2}x)}\).
(c) \(x^2-2\sqrt{2}x\tan{(\sqrt{2}x)}\).
(d) \(x^2-2\sqrt{2}x\coth{(\sqrt{2}x)}\).
Check Answer
Option b
Q.No:14 JEST-2017
\(\phi_0(x)\) and \(\phi_1(x)\) are respectively the orthonormal wavefunctions of the ground and first excited states of a one dimensional simple harmonic oscillator. Consider the normalised wave function \(\psi(x)=c_0 \phi_0(x)+c_1 \phi_1(x)\), where \(c_0\) and \(c_1\) are real. For what values of \(c_0\) and \(c_1\) will \(\langle \psi(x)|x|\psi(x)\rangle\) be maximized?
(a) \(c_0=c_1=+1/\sqrt{2}\)
(b) \(c_0=-c_1=+1/\sqrt{2}\)
(c) \(c_0=+\sqrt{3}/2, c_1=+1/2\)
(d) \(c_0=+\sqrt{3}/2, c_1=-1/2\)
Check Answer
Option a
Q.No:15 JEST-2017
What is the dimension of \(\frac{\hbar}{i}\frac{\partial \psi}{\partial x}\), where \(\psi\) is a wavefunction in two dimensions?
(a) kg \(m^{-1} s^{-2}\)
(b) kg \(s^{-2}\)
(c) kg \(m^{2} s^{-2}\)
(d) kg \(s^{-1}\)
Check Answer
Option d
Q.No:16 JEST-2018
A one dimensional harmonic oscillator (mass \(m\) and frequency \(\omega\)) is in a state \(\psi\) such that the only possible outcomes of an energy measurement are \(E_0, E_1\) or \(E_2\), where \(E_n\) is the energy of the \(n\)-th excited state. If \(H\) is the Hamiltonian of the oscillator, \(\langle \psi|H|\psi\rangle=3\hbar \omega/2\) and \(\langle \psi|H^2|\psi\rangle=11\hbar^2\omega^2/4\), then the probability that the energy measurement yields \(E_0\) is
(a) \(1/2\)
(b) \(1/4\)
(c) \(1/8\)
(d) \(0\)
Check Answer
Option b
Q.No:17 JEST-2019
A quantum particle of mass \(m\) is in a one dimensional potential of the form
\[
V(x)=
\left\{
\begin{array}{ll}
\frac{1}{2}m\omega^2 x^2, & \text{if }x>0 \\
\infty, & \text{if }x\leq 0,
\end{array}
\right.
\]
where \(\omega\) is a constant. Which one of the following represents the possible ground state wave function of the particle?

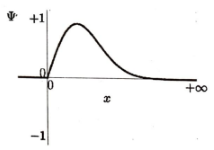

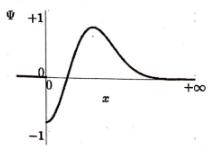
Check Answer
Option b
Q.No:18 JEST-2019
The wave function \(\psi(x)=A\exp{\left(-\frac{b^2 x^2}{2}\right)}\) (for real constants \(A\) and \(b\)) is a normalized eigenfunction of the Schrodinger equation for a particle of mass \(m\) and energy \(E\) in a one dimensional potential \(V(x)\) such that \(V(x)=0\) at \(x=0\). Which one of the following is correct?
(a) \(V=\frac{\hbar^2 b^4 x^2}{m}\)
(b) \(V=\frac{\hbar^2 b^4 x^2}{2m}\)
(c) \(E=\frac{\hbar^2 b^2}{4m}\)
(d) \(E=\frac{\hbar^2 b^2}{m}\)
Check Answer
Option b
Q.No:19 JEST-2019
Consider a quantum particle in a one-dimensional box of length \(L\). The coordinates of the leftmost wall of the box is at \(x=0\) and that of the rightmost wall is at \(x=L\). The particle is in the ground state at \(t=0\). At \(t=0\), we suddenly change the length of the box to \(3L\) by moving the right wall. What is the probability that the particle is in the ground state of the new system immediately after the change?
(a) \(0.36\)
(b) \(\frac{9}{8\pi}\)
(c) \(\frac{81}{64\pi^2}\)
(d) \(\frac{0.5}{\pi}L\)
Check Answer
Option c
Q.No:20 JEST-2019
A one-dimensional harmonic oscillator is in the state
\[
|\psi\rangle=\sum_{n=0}^{\infty} \frac{1}{\sqrt{n!}}|n\rangle,
\]
where \(|n\rangle\) is the normalized energy eigenstate with eigenvalue \((n+\frac{1}{2})\hbar \omega\). Let the expectation value of the Hamiltonian in the state \(|\psi\rangle\) be expressed as \(\frac{1}{2}\alpha \hbar \omega\). What is the value of \(\alpha\)?
Check Answer
Ans 3
Q.No:21 JEST-2020
The wave function of an electron in one dimension is given by
\[
\psi(x)=
\left\{
\begin{array}{ll}
0, & \text{for }x<0 \\
2\sqrt{3}e^{-x}(1-e^{-x}), & \text{for }x\geq 0.
\end{array}
\right.
\]
The ratio between the expected position \(\langle x\rangle\) and the most probable position \(x_m\) is:
(a) \(0.856\)
(b) \(1.563\)
(c) \(2.784\)
(d) \(3.567\)
Check Answer
Option b
Q.No:22 JEST-2020
A two-state quantum system has energy eigenvalues \(\pm \epsilon\) corresponding to normalised states \(\psi_{\pm}\). At time \(t=0\) the system is in the quantum state \([\psi_{+}+\psi_{-}]/\sqrt{2}\). Find the \(10000\times \) probability that the system will be in the same state at time \(t=h/(6\epsilon)\), where \(h\) is the Planck's constant.
Check Answer
Ans 2500
Q.No:23 JEST-2021
A particle with energy \(E\) is in a bound state of the one-dimensional Hamiltonian \(H=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)\). The expectation value of momentum \(\langle p\rangle\)
(a) is always zero.
(b) depends on the degeneracy of the eigenstate.
(c) is zero if and only if the potential is symmetric \(V(-x)=V(x)\).
(d) depends on the energy \(E\) of the eigenstate.
Check Answer
Option c
Q.No:24 JEST-2021
Consider the normalized wave function \(\psi=a\psi_0+b\psi_1\) for a one-dimensional simple harmonic oscillator at some time, where \(\psi_0\) and \(\psi_1\) are the normalized ground state and the first excited state respectively, and \(a, b\) are real numbers. For what values of \(a\) and \(b\), the magnitude of expectation value of \(x\), i.e. \(|\langle x\rangle|\), is maximum?
(a) \(a=-b=1/\sqrt{2}\)
(b) \(a=b=1/\sqrt{2}\)
(c) \(a=1, b=0\)
(d) \(a=0, b=1\)
Check Answer
Option b
Q.No:25 JEST-2021
A particle is in the \(n\)th energy eigenstate of an infinite one-dimensional potential well between \(x=0\) and \(x=L\). Let \(P\) be the probability of finding the particle between \(x=0\) and \(x=1/3\). In the limit \(n\to \infty\), the value of \(P\) is
(a) \(1/9\)
(b) \(2/3\)
(c) \(1/3\)
(d) \(1/\sqrt{3}\)
Check Answer
Option c
Q.No:26 JEST-2021
The uncertainty \(\Delta x\) in the position of a particle with mass \(m\) in the ground state of a harmonic oscillator is \(2\hbar/mc\). What is the energy (in units of \(10^{-4} mc^2\)) required to excite the system to the first excited state?
Check Answer
Ans 1250
Q.No:27 JEST-2022
A beam of high energy neutrons is scattered from a metal lattice, where the spacing between nuclei is around \(0.4 nm\). In order to see quantum diffraction effects, the kinetic energy of the neutrons must be of the order [\(\text{Mass of neutron} = 1.67 \times 10^{-27} kg, \text{Planck's constant}=6.62 \times 10^{-34} m^2 kg s^{-1}\)]
(a) meV
(b) MeV
(c) eV
(d) keV
Check Answer
Option a
Q.No:28 JEST-2022
A particle of mass \(m\) moves in one dimension. The exact eigenfunction for the ground state of the system is
\[
\psi(x)=\frac{A}{\cosh{(\lambda x)}},
\]
where, \(\lambda\) is a constant and \(A\) is the normalization constant. If the potential \(V(x)\) vanishes at infinity, the ground state energy of the system is
(a) \(-\frac{\hbar^2 \lambda^2}{2m}\)
(b) \(\frac{\hbar^2 \lambda^2}{2m}\)
(c) \(\frac{\hbar^2 \lambda}{2m}\)
(d) \(-\frac{\hbar^2 \lambda}{2m}\)
Check Answer
Option a
Q.No:29 JEST-2022
The frequency dispersion relation of the surface waves of a fluid of density \(\rho\) and temperature \(T\), is given by \(\omega^2=gk + Tk^3/\rho\), where \(\omega\) and \(k\) are the angular frequency and wavenumber, respectively, \(g\) is the acceleration due to gravity. The first term in r.h.s. describes the gravity waves and the second term describes the surface tension wave. What is the ratio of the first term to the second term, when the phase velocity is equal to the group velocity?
Check Answer
Ans 1
Q.No:30 JEST-2023
Consider a particle subjected to the symmetric one-dimensional infinite square well potential:
\[
V(x)=
\left\{
\begin{array}{ll}
0, & |x|\leq \frac{L}{2} \\
\infty, & |x|> \frac{L}{2}
\end{array}
\right.
\]
Find the time evolution of the wavefunction \(\psi(x,t)\), if at time \(t = 0\) the particle is prepared in an equal superposition of the ground and the first excited states:
\[\psi(x,0)=\frac{1}{\sqrt{2}}(\phi_1(x)+\phi_2(x))\]
where \(\phi_1(x)\) and \(\phi_2(x)\) are normalized eigenfunctions of the ground state and the first excited state respectively. If \(\tau\) is the smallest time at which the particle is equally likely to be in either
half of the well, select the correct value of
\[\frac{\tau h}{mL^2},\]
where \(h\) is the Planck’s constant, \(m\) is the mass of the particle and \(L\) is the width of the well as defined above.
1) \(\frac{2}{3}\)
2) \(\frac{1}{3}\)
3) \(\frac{1}{6}\)
4) \(\frac{4}{3}\)
Check Answer
Option 1
Q.No:31 JEST-2023
A quantum particle moving in one dimension is in a state having the wave function
\[\psi(x)=sinh(\lambda x) \hspace{0.5mm} \text{exp} \hspace{0.5mm} (\frac{-ax^4 +bx+ipx}{\hbar})\]
where \(a, b, \lambda\) and \(p\) are all positive real numbers. What is the expectation value of momentum?
1) \(\hbar \lambda\)
2) \(p\)
3) \(b\)
4) \(-p\)
Check Answer
Option 2
Q.No:32 JEST-2024
What is the power of a light source emitting photons of wavelength 600 nm at the rate of one photon per second? Planck’s constant \( h = 6.6 \times 10^{-34} \) Joule sec and speed of light \( c = 3 \times 10^8 \) m/sec.
1) \( 3.3\times10^{-19} \) W
2) \( 3.3\times10^{-18} \) W
3) \( 6.0\times10^{-19} \) W
4) \( 6.0\times10^{-18} \) W
Check Answer
Option 1
Q.No: 33 JEST-2024
A particle moving in one dimension has the wave function
\[
\psi(x) = \exp \left[ -\alpha \left( x - \frac{i k_0}{\alpha} \right)^2 \right] \sin^2(k_1 x),
\]
where \( \alpha \) is real positive and \( k_0 \), \( k_1 \) are real. The expectation value of momentum is
1) \( 2\hbar k_0 \)
2) \( 0 \)
3) \( \hbar k_0 \)
4) \( \hbar k_1 \)
Check Answer
Option 1
Q.No: 34 JEST-2024
A quantum mechanical particle of mass \( m \) is confined in a one dimensional infinite potential well whose walls are located at \( x = 0 \) and \( x = 1 \). The wave function of the particle inside the well is \( \psi(x) = N [{x \ln x + (1 - x) \ln(1 - x)}] \) for some normalization constant \( N \). An experimentalist measures the position of the particle on an ensemble of a large number of identical systems in the same state. The mean of the outcomes is found to be \( \frac{1}{n} \), where \( n \) is an integer. What is \( n \)?
Check Answer
Ans 2
Q.No: 35 JEST-2024
A quantum harmonic oscillator of mass \( m \) and angular frequency \( \omega \) is in the state \( |\psi\rangle = \frac{1}{\sqrt{2}}(|287\rangle + |288\rangle) \), where \( |n\rangle \) denotes the \( n^{th} \) normalized energy eigenstate of the harmonic oscillator. Let \( L_0 = \sqrt{\frac{\hbar}{m\omega}} \) denote the oscillator size and \( \langle \hat{x} \rangle \) denote the expectation value of the position operator in the state \( |\psi\rangle \). What is the value of \( \frac{\langle \hat{x} \rangle}{L_0} \)? You may use the form of the position operator in terms of the raising and lowering operators: \( \hat{x} = \frac{L_0}{\sqrt{2}}(a + a^\dagger) \).
Check Answer
Ans 12
Q.No: 36 JEST-2024
A classical particle undergoing simple harmonic motion is confined to the region \((-a, a)\) on the X-axis. If a snapshot of the particle is taken at a random instant of time, what is the probability that it would be found in the region \( \left(\frac{a}{2}, a\right) \)?
1) \( \frac{1}{4} \)
2) \( \frac{1}{6} \)
3) \( \frac{1}{3} \)
4) \( \frac{2}{5} \)
Check Answer
Option 3
Q.No: 37 JEST-2024
A quantum particle is subjected to the potential \( V(x) = ax + b x^2 \), where \( a \) and \( b \) are constants. What is the mean position of the particle in the first excited state?
1) \( \frac{a}{2b} \)
2) \( -\frac{a}{2b} \)
3) \( -\frac{a}{b} \)
4) \( \frac{a}{b} \)
Check Answer
Option 2
Q.No: 38 JEST-2025
Consider the time-independent Schrödinger equation with a real potential and suppose \(\psi(x)\) is a solution of this equation. Which of the following is true?
1) \(\psi^{*}\) is never a solution of the same equation.
2) \(\psi^{*}\) is a solution of the same equation.
3) \(\psi^{*}\) is a solution of the same equation only if the potential is symmetric about \(x = 0\).
4) \(\psi^{*}\) is a solution of the same equation only if the potential vanishes at infinity.
Check Answer
Option 2
Q.No: 39 JEST-2025
Match the following statements.
A1) Photoelectric effect
B1) Involves loosely bound or free electrons
A2) Compton scattering
B2) Inverse photoelectric effect
A3) Pair production
B3) Needs a minimum of 1.02 MeV of energy for the incident radiation
A4) Bremsstrahlung
B4) Involves bound electrons and depends on the specifics of the material
1) A1–B3,A2–B4,A3–B2,A4–B1
2) A1–B4,A2–B1,A3–B3,A4–B2
3) A1–B4,A2–B3,A3–B2,A4–B1
4) A1–B3,A2–B2,A3–B1,A4–B4
Check Answer
Option 2
Q.No: 40 JEST-2025
For a particle in a one-dimensional box of width \(L\), the uncertainty \(\Delta p\) in momentum in the \(n\)-th eigenstate of energy for large \(n\) is
1) \(\frac{n\pi\hbar}{L}\)
2) \(\frac{2n\pi\hbar}{L}\)
3) \(\frac{2n\hbar}{L}\)
4) \(\frac{\hbar}{n\pi L}\)

Q.No.1 Discussion :
Ans
Q.No.2 Discussion :
Answer
Q.No.3 Discussion :
ans option A
Q.No.4 Discussion :
My solution
Q.No.5 Discussion :
Option b
Q.No.6 Discussion :
Ans
Q.No.7 Discussion :
Ans
Q.No.8 Discussion :
Ans
Q.No.9 Discussion :
Ans
Q.No.10 Discussion :
QNO10
Q.No.11 Discussion :
Ans
Q.No.12 Discussion :
Option C
Q.No.13 Discussion :
Q.No.14 Discussion :
https://acrobat.adobe.com/id/urn:aaid:sc:AP:7f5377f0-a0e7-450e-8d7a-1c31d53d354e
solution
Q.No.15 Discussion :
Answer: D
Q.No.16 Discussion :
solution
Q.No.17 Discussion :
Q.No.18 Discussion :
Q.No.19 Discussion :
Answer
Q.No.20 Discussion :
Q.No.21 Discussion :
solution
continued
Q.No.22 Discussion :
Ans
Q.No.23 Discussion :
Q.No.24 Discussion :
Page 1
Page 2
Q.No.25 Discussion :
QN25
Q.No.26 Discussion :
Answer: 1250
Q.No.27 Discussion :
ans option A
Q.No.28 Discussion :
Answer
My solution
Q.No.29 Discussion :
Required ratio is 1