Basics TISE 1D Box and LHO TIFR - S. N. Bose Physics Learning Center

Q.No:1 TIFR-2013

The value of the integral \[ \int_{0}^{\infty} dx x^9 \exp{(-x^2)} \] is

(a)\(20160\)

(b) \(12\)

(d) \(24\)

Check Answer

Option b

Q.No:2 TIFR-2013

In a quantum mechanical system, an observable \(A\) is represented by an operator \(\hat{A}\). If \(|\psi\rangle\) is a state of the system, but not an eigenstate of \(\hat{A}\), then the quantity \[ r=\langle \psi|\hat{A}|\psi\rangle^2-\langle \psi|\hat{A}^2|\psi\rangle \] satisfies the relation

Check Answer

Option a

Q.No:3 TIFR-2013

A particle of energy \(E\) moves in one dimension under the influence of a potential \(V(x)\). If \(E>V(x)\) for some range of \(x\), which of the following graphs can represent a bound state wave function of the particle?

Check Answer

Option a

Q.No:4 TIFR-2013

In a Davisson-Germer experiment, a collimated beam of electrons of energy \(54 eV\), at normal incidence on a given crystal, shows a peak at a reflection angle of \(40^{\circ}\). If the electron beam is replaced by a neutron beam, and the peak appears at the same value of reflection angle, then the energy of the neutrons must be

(a) \(330 eV\)

(b) \(33 eV\)

(d) \(0.03 eV\)

Check Answer

Option d

Q.No:5 TIFR-2013

A harmonic oscillator has the wave function, \[ \psi(x, t)=\frac{1}{5}[3\varphi_0(x, t)-2\sqrt{2}\varphi_1(x, t)+2\sqrt{2}\varphi_2(x, t)] \] where \(\varphi_n(x, t)\) is the eigenfunction belonging to the \(n\)-th energy eigenvalue \((n+\frac{1}{2})\hbar \omega\). The expectation value \(\langle E\rangle\) of energy for the state \(\psi(x, t)\) is

(a) \(1.58\hbar \omega\)

(b) \(0.46\hbar \omega\)

(d) \(1.46\hbar \omega\)

Check Answer

Option d

Q.No:6 TIFR-2013

A binary star is observed to consist of a blue star \(B\) (peak wavelength \(400 nm\)) and a red star \(R\) (peak wavelength \(800 nm\)) orbiting each other. As observed from the Earth, \(B\) and \(R\) appear equally bright. Assuming that the stars radiate as perfect blackbodies, it follows that the ratio of volumes \(V_B/V_R\) of the two stars is

(a) \(1/64\)

(b) \(64\)

(d) \(1/16\)

Check Answer

Option a

Q.No:7 TIFR-2014

The probability function for a variable \(x\) which assumes only positive values is \[ f(x)=x\exp{\left(-\frac{x}{\lambda}\right)} \] where \(\lambda>0\). The ratio \(\langle x\rangle/\hat{x}\), where \(\hat{x}\) is the most probable value and \(\langle x\rangle\) is the mean value of the variable \(x\), is

(a) \(2\)

(b) \(\frac{1+\lambda}{1-\lambda}\)

(d) \(1\)

Check Answer

Option a

Q.No:8 TIFR-2014

A particle moving in one dimension has the un-normalised wave function \[ \psi(x)=x\exp{\left(-\frac{x^2}{\lambda^2}\right)} \] where \(\lambda\) is a real constant. The expectation value of its momentum is \(\langle p\rangle=\)

(a) \(\frac{\hbar}{\lambda}\exp{\left(-\frac{x^2}{\lambda^2}\right)}\)

(b) \(\frac{\hbar^2}{\lambda^2}-2\frac{\hbar}{\lambda}\)

(d) zero

Check Answer

Option d

Q.No:9 TIFR-2015

Two blackbodies radiate energy at temperatures \(T_1\) and \(T_2\) (\(T_1>T_2\)). The energy emitted per unit time per unit solid angle per unit surface area of a blackbody in the frequency range \(\nu\) to \(\nu+d\nu\) is given by \(B(\nu)d\nu\). Which one of the following graphs has the correct form?

Check Answer

Option d

Q.No:10 TIFR-2015

A particle is moving in one dimension under a potential \(V(x)\) such that, for large positive values of \(x\), \(V(x)\approx kx^{\beta}\), where \(k>0\) and \(\beta \geq 1\). If the wavefunction in this region has the form \(\psi(x)\sim \exp{(-x^{\lambda})}\), which of the following is true?

(a) \(\lambda=\frac{\beta}{2}+1\)

(b) \(\lambda=\beta\)

(d) \(\lambda=\frac{\beta^2}{2}\)

Check Answer

Option a

Q.No:11 TIFR-2015

A one-dimensional quantum harmonic oscillator is in its ground state \[ \psi_0(x)=\left(\frac{m\omega}{\pi \hbar}\right)^{1/4}e^{-m\omega x^2/2\hbar} \] Two experiments, [A] and [B], are performed on the system. In [A], the frequency \(\omega\) of the oscillator is suddenly doubled, while in [B] the frequency \(\omega\) is suddenly halved. If \(p_A\) and \(p_B\) denote the probability in each case that the system is found in its new ground state immediately after the frequency change, which of the following is true?

(a) \(p_A=\sqrt{2}p_B\)

(b) \(p_A=2p_B\)

(d) \(p_A=p_B\)

Check Answer

Option d

Q.No:12 TIFR-2015

A two-state quantum system has two observables \(A\) and \(B\). It is known that the observable \(A\) has eigenstates \(|\alpha_1\rangle\) and \(|\alpha_2\rangle\) with eigenvalues \(a_1\) and \(a_2\) respectively, while \(B\) has eigenstates \(|\beta_1\rangle\) and \(|\beta_2\rangle\) with eigenvalues \(b_1\) and \(b_2\) respectively, and that these eigenstates are related by \[ |\beta_1\rangle=\frac{3}{5}|\alpha_1\rangle-\frac{4}{5}|\alpha_2\rangle ~ |\beta_2\rangle=\frac{4}{5}|\alpha_1\rangle+\frac{3}{5}|\alpha_2\rangle \] Suppose a measurement is made of the observable \(A\) and a value \(a_1\) is obtained. If the observable \(B\) is now measured, the probability of obtaining the value \(b_1\) will be

(a) \(0.80\)

(b) \(0.64\)

(d) \(0.36\)

Check Answer

Option d

Q.No:13 TIFR-2016

If \(x\) is a continuous variable which is uniformly distributed over the real line from \(x=0\) to \(x\to \infty\) according to the distribution \[ f(x)=\exp{(-4x)} \] then the expectation value of \[ \cos{4x} \] is

(a) zero

(b) \(1/2\)

(d) \(1/16\)

Check Answer

Option b

Q.No:14 TIFR-2016

A one-dimensional harmonic oscillator of mass \(m\) and natural frequency \(\omega\) is in the quantum state \[ |\psi\rangle=\frac{1}{\sqrt{3}}|0\rangle+\frac{i}{\sqrt{3}}|1\rangle+\frac{i}{\sqrt{3}}|2\rangle \] at time \(t=0\), where \(|n\rangle\) denotes the eigenstate with eigenvalue \(\left(n+\frac{1}{2}\right)\hbar \omega\). It follows that the expectation value \(\langle x\rangle\) of the position operator \(\hat{x}\) is

(a) \(x(0)\left[\cos{\omega t}+\frac{1}{\sqrt{3}}\sin{\omega t}\right]\)

(b) \(x(0)\left[\cos{\omega t}-\sin{\omega t}\right]\)

(d) \(x(0)\left[\cos{\omega t}+\frac{1}{\sqrt{2}}\sin{\omega t}\right]\)

Check Answer

Option d

Q.No:15 TIFR-2016

Two harmonic oscillators \(A\) and \(B\) are in excited eigenstates with the same excitation energy \(E\), as measured from their respective ground state energies. The natural frequency of \(A\) is twice that of \(B\).

If the wavefunction of \(B\) is as sketched in the above picture, which of the following would best represent the wavefunction of \(A\)?

Check Answer

Option b

Q.No:16 TIFR-2016

A particle is confined in a one-dimensional box of unit length, i.e. \(L=1\), i.e. in a potential \[ V(x)= \left\{ \begin{array}{ll} 0 & \text{if }0<x<1 \\ \infty & \text{otherwise} \end{array} \right. \] The energy eigenvalues of this particle are denoted \(E_0, E_1, E_2, E_3, ...\)

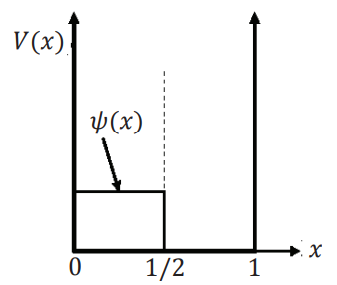
In a particular experiment, the wavefunction of this particle, at \(t=0\), is given by \[ \psi(x)= \left\{ \begin{array}{ll} \sqrt{2} & \text{if }0<x<1/2 \\ 0 & \text{otherwise} \end{array} \right. \] If, simultaneously, i.e. at \(t=0\), a measurement of the energy of the particle is made, find \(100p_3\), where \(p_3\) is the probability that the measurement will yield the energy \(E_3\).

Check Answer

Ans 0

Q.No:17 TIFR-2017

The normalized wave function of a particle can be written as \[ \Psi(x)=N\sum_{n=0}^{\infty} \left(\frac{1}{\sqrt{7}}\right)^n \varphi_n(x) \] where \(\varphi_n(x)\) are the normalized energy eigenfunctions of a given Hamiltonian. The value of \(N\) is

(a) \(\sqrt{1/7}\)

(b) \(\sqrt{6/7}\)

(d) \(\sqrt{(6-2\sqrt{7})/7}\)

Check Answer

Option b

Q.No:18 TIFR-2017

A particle of mass \(m\), confined to one dimension \(x\), is in the ground state of a harmonic oscillator potential with a normalized wave function \[ \Psi_0(x)=\left(\frac{2a}{\pi}\right)^{\frac{1}{4}}e^{-ax^2} \] where \(a=m\omega/2\hbar\). Find the expectation value of \(x^8\) in terms of the parameter \(a\).

Check Answer

Ans 105 by(256 into a^4

Q.No:19 TIFR-2018

A particle is confined inside a one-dimensional box of length \(\ell\) and left undisturbed for a long time. In the most general case, its wave-function MUST be

(a) the ground state of energy.

(b) periodic, where \(\ell\) equals an integer number of periods.

(d) any one of the energy eigenfunctions.

Check Answer

Option c

Q.No:20 TIFR-2018

The wave-function \(\Psi\) of a particle in a one-dimensional harmonic oscillator potential is given by \[ \Psi=\left(\frac{1}{\pi \ell^2}\right)^{1/4}\left(1+\frac{\sqrt{2}x}{\ell}\right)\exp{\left(-\frac{x^2}{2\ell^2}\right)} \] where \(\ell=100 \hspace{1mm}\mu \text{m}\). Find the expectation value of the position \(x\) of this particle, in \(\mu \text{m}\).

Check Answer

Ans 71

Q.No:21 TIFR-2018

Evaluate the integral \[ \int_{-\infty}^{\infty} dx \exp{(-x^2)}\cos{(\sqrt{2}x)} \]

Q.No:22 TIFR-2019

The sketch shown below illustrates the apparatus and results for a famous experiment. The graph on the right is a polar plot of the number of electrons received in the detector.

From the result, the experimenters were able to conclude that

(a) the energy levels of atoms in a metal are quantized.

(b) electrons in a beam can behave as waves.

(d) there are magnetic domains inside a nickel sample.

Check Answer

Option b

Q.No:23 TIFR-2019

At time \(t=0\), the wavefunction of a particle in a harmonic oscillator potential of natural frequency \(\omega\) is given by \[ \psi(0)=\frac{1}{5}\{3\varphi_0-2\sqrt{2}\varphi_1+2\sqrt{2}\varphi_2\} \] where \(\varphi_n(x)\) denotes the eigenfunction belonging to the \(n\)-th eigenvalue of energy. At time \(t=\tau\), the wavefunction is found to be \[ \psi(\tau)=-\frac{i}{5}\{3\varphi_0+2\sqrt{2}\varphi_1+2\sqrt{2}\varphi_2\} \] The minimum value of \(\tau\) is

(a) \(\frac{\pi}{2\omega}\)

(b) \(\frac{2\pi}{\omega}\)

(d) \(\frac{\pi}{\omega}\)

Check Answer

Option d

Q.No:24 TIFR-2020

A particle of mass \(m\) is confined inside a box with boundaries at \(x=\pm L\). The ground state and the first excited state of this particle are \(E_1\) and \(E_2\) respectively. Now a repulsive delta function potential \(\lambda \delta(x)\) is introduced at the centre of the box where the constant \(\lambda\) satisfies \[ 0<\lambda \ll \frac{1}{32m}\left(\frac{h}{L}\right)^2 \] If the energies of the new ground state and the new first excited state be denoted as \(E_1'\) and \(E_2'\) respectively, it follows that

(a) \(E_1'>E_1, E_2'>E_2\)

(b) \(E_1'=E_1, E_2'=E_2\)

(d) \(E_1'=E_1, E_2'>E_2\)

Check Answer

Option c

Q.No:25 TIFR-2020

A particle of mass \(m\) is placed in a one-dimensional harmonic oscillator potential \[ V(x)=\frac{1}{2}m\omega^2 x^2 \] At \(t=0\), its wavefunction is \(\psi(x)\). At \(t=2\pi/\omega\) its wavefunction will be

(a) \(\psi(x)\)

(b) \(-\psi(x)\)

(d) \(\frac{2\pi}{\omega}\psi(x)\)

Check Answer

Option b

Q.No:26 TIFR-2018

Given a particle confined in a one-dimensional box between \(x=-a\) and \(x=+a\), a student attempts to find the ground state by assuming a wave-function \[ \psi(x)= \left\{ \begin{array}{ll} A(a^2-x^2)^{3/2} & \text{for }|x|\leq a \\ 0 & \text{for }|x|>a \end{array} \right. \] The ground state energy \(E_m\) is estimated by calculating the expectation value of energy with this trial wave-function. If \(E_0\) is the true ground state energy, what is the ratio \(E_m/E_0\)?

Check Answer

Ans

Q.No:27 TIFR-2018

A beam of high energy neutrons is scattered from a metal lattice, where the spacing between nuclei is around \(0.4 \hspace{1mm}\text{nm}\). In order to see quantum diffraction effects, the kinetic energy of the neutrons must be around

(a) \(7.85 \hspace{1mm}\text{MeV}\)

(b) \(5.11 \hspace{1mm}\text{meV}\)

(d) \(78.5 \hspace{1mm}\text{eV}\)

Check Answer

Option b

Q.No:28 TIFR-2021

The wave function of a one-dimensional particle of mass \(m\) is shown below. The average kinetic energy of the particle can be written as

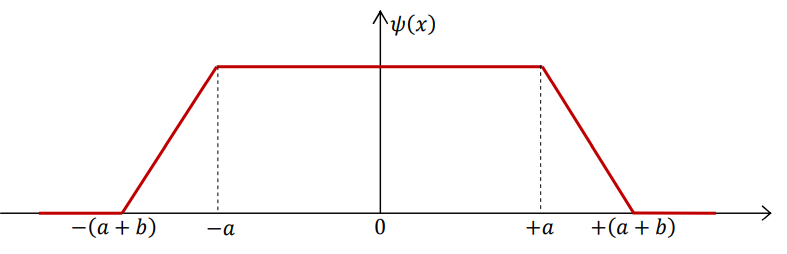
(a) \(\frac{3\hbar^2}{2mb(3a+b)}\)

(b) \(0\)

(d) \(\frac{\hbar^2}{2mb(a+b)}\)

Check Answer

Option a

Q.No:30 TIFR-2021

Suppose a system is in a normalised state \(|\Psi\rangle\) such that \[ |\Psi\rangle=c(|\varphi_0\rangle+e^{i\theta}|\varphi_1\rangle) \] where \(|\varphi_0\rangle\) and \(|\varphi_1\rangle\) are the first two normalised eigenstates of a one-dimensional simple harmonic oscillator of frequency \(\omega\), and \(c>0\) is a real constant. If the expectation value of the position operator \(\hat{x}\) is given by \[ \langle \Psi|\hat{x}|\Psi\rangle=\frac{1}{2}\sqrt{\frac{\hbar}{m\omega}} \] the value of \(\theta\) must be

(a) \(\pi/4\)

(b) \(\pi/2\)

(d) \(\pi\)

Check Answer

Option a

Q.No:31 TIFR-2023

Consider an electron double slit experiment as shown in the figure below, with slits \(S_1\) and \(S_2\).

If now, within the shaded region marked \(C\), a constant uniform magnetic field pointing outside the page is turned on, the fringe pattern

(a) will remain unchanged.

(b) will become dimmer

(d) will get shifted.

Check Answer

Option d

Q.No:32 TIFR-2023

A random positive variable \(x\) follows an exponential distribution \[p(x) \propto e^{-\lambda x}\] with \(\lambda >0\). The probability of observing an event \(x> 3 \langle x \rangle \), where \(\langle x \rangle\) represents the average value of \(x\), is

(a) \(1/e^3\)

(b) \(1/e^4\)

(d) \(1/e^2\)

Check Answer

Option a

Q.No:33 TIFR-2023

A particle is in the ground state of a one-dimensional box \[-\frac{L}{2} \leq x \leq +\frac{L}{2}\] The uncertainty product \(\Delta x\Delta p\) for this state satisfies

(a) \(\frac{\hbar}{2} < \Delta x\Delta p < \hbar\)

(b) \(\hbar < \Delta x\Delta p < \frac{3\hbar}{2}\)

(d) \(\Delta x\Delta p =\frac{\hbar}{2}\)

Check Answer

Option a

Q.No:34 TIFR-2023

The equilibrium temperature \((T_0)\) on the surface of a planet results from the balance between the energy received from their host star and the energy they emit back into space. In the case of the Earth, \(T_0\) = 300 K and the orbit is almost circular. We may safely assume that planets absorb and emit radiation like perfect blackbodies Now consider an exoplanet of the same size as the Earth, which orbits a fainter star having a power output only \(25\%\) of that of the Sun, in an almost-circular orbit of radius \(25\%\) that of the Earth-Sun distance. The equilibrium temperature \(T'_0\) on the surface of this exoplanet will be about

Now consider an exoplanet of the same size as the Earth, which orbits a fainter star having a power output only \(25\%\) of that of the Sun, in an almost-circular orbit of radius \(25\%\) that of the Earth-Sun distance.

The equilibrium temperature \(T'_0\) on the surface of this exoplanet will be about

(a) 424 K

(b) 212 K

(d) 600 K

Check Answer

Option a

Q.No:35 TIFR-2023

A well-collimated constant-current electron beam of Gaussian energy distribution centred at 10 eV with FWHM of 2 eV is detected using a metal cup connected to an ammeter, as shown in the figure below. The entire apparatus is kept in vacuum.

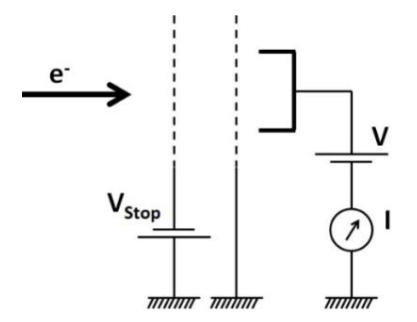
To measure the energy width of the electron beam, a grid is introduced with a voltage source\(V_{stop}\) connected to it, as shown in the figure. The current measured in the cup is plotted as a function of the value of \(V_{stop}\). The graph of the current I vs \(V_{stop}\) would be

Check Answer

Option a

Q.No:36 TIFR-2023

A photon of frequency \(v_i\) collides “head on” with an electron of mass \(m\) having speed \(u_i\) and the photon scatters off in a direction exactly opposite to its initial momentum (see figure).

It is found that the frequency of the scattered photon is the same as that of the incident photon. Which of the following conditions must hold for this to happen?

(a) The magnitude of the initial momentum of the electron is \(p_i ^e=hv_i/c\)

(b) The initial energy of the electron is \(E_i ^e=hv_i\)

(d) The initial energy of the electron is \(E_i ^e=2hv_i\)

Check Answer

Option a

Q.No:37 TIFR-2024

Consider a particle of mass \( m \) moving in an infinite one-dimensional potential well of length \( L \) between points \( A \) and \( B \). In a quantum-mechanical treatment, the particle is in the ground state with an energy \( E_g \). The wall at \( B \) is suddenly shifted to \( B' \) where \( AB' \) has length \( 2L \). If we measure the energy again, what is the most probable result?

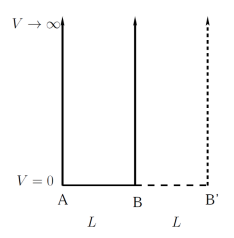
1) \( E_g \)

2) \( \frac{E_g}{4} \)

3) \( 4E_g \)

4) \( \frac{9E_g}{4} \)

Check Answer

Option 1

Q.No:38 TIFR-2024

The un-normalized energy eigenfunction of a one-dimensional simple quantum harmonic oscillator in dimensionless units (\(m = \hbar = \omega = 1\)) is \[ \psi_a(x) = (2x^3 - 3x)e^{-x^2/2} \] Which of the following are two other (un-normalized) eigenfunctions which are closest in energy to \(\psi_a\)?

1) \( (2x^2 - 1)e^{-x^2/2}; (4x^4 - 12x^2 + 3)e^{-x^2/2} \)

2) \( e^{-x^2/2}; (2x^2 - 1)e^{-x^2/2} \)

3) \( x e^{-x^2/2}; (4x^5 - 20x^3 + 15x)e^{-x^2/2} \)

4) \( (2x^2 - 1)e^{-x^2/2}; (4x^5 + 20x^3 + 15x)e^{-x^2/2} \)

Check Answer

Option 1

Q.No:39 TIFR-2024

Consider a particle of mass \( m \) moving in a one-dimensional potential of the form \[ V(x) = \begin{cases} \frac{1}{2}kx^2 & \text{for } x > 0 \\ \infty & \text{for } x \leq 0 \end{cases} \] In a quantum mechanical treatment, what is the ground state energy of the particle?

1) \( \frac{3}{2} \sqrt{\frac{\hbar^2 k}{m}} \)

2) \( \frac{1}{2} \sqrt{\frac{\hbar^2 k}{m}} \)

3) \( \sqrt{\frac{\hbar^2 k}{m}} \)

4) \( \frac{5}{2} \sqrt{\frac{\hbar^2 k}{m}} \)

Check Answer

Option 1

Q.No:40 TIFR-2024

A particle of mass \( m \) moving in 1 dimension has the wavefunction \[ \psi(x) = \frac{1}{\pi^{1/4}\sqrt{a}} e^{ipx/\hbar} e^{-x^2/2a^2} \] Its average kinetic energy is given by (You might find the following integral useful: \( \int_{-\infty}^{+\infty} dx \, e^{-\alpha x^2} = \sqrt{\frac{\pi}{\alpha}} \) for \( \alpha > 0 \))

1) \( \frac{p^2}{2m} + \frac{\hbar^2}{4a^2m} \)

2) \( \frac{\left( p + \frac{\sqrt{\pi}\hbar}{a} \right)^2}{2m} \)

3) \( \frac{\left( -p + \frac{\sqrt{\pi}\hbar}{a} \right)^2}{2m} \)

4) \( \frac{p^2}{2m} + \frac{\hbar^2}{4a^2m} + \frac{p\hbar}{2ma} \)

Check Answer

Option 1

Q.No:41 TIFR-2025

For a one–dimensional quantum harmonic oscillator, at time \(t = 0\), the particle is in the ground state. What is the expectation value of the position and momentum operator at time \(t\)?

1) \(\langle x(t)\rangle = \langle p(t)\rangle = 0\)

2) \(\langle x(t)\rangle = \sqrt{\frac{\hbar}{m\omega}}\,\sin \omega t,\ \langle p(t)\rangle = 0\)

3) \(\langle x(t)\rangle = \sqrt{\frac{\hbar}{m\omega}}\,\sin \omega t,\ \langle p(t)\rangle = \sqrt{\hbar m\omega}\,\cos \omega t\)

4) \(\langle x(t)\rangle = 0,\ \langle p(t)\rangle = \sqrt{\hbar m\omega}\,\cos \omega t\)

Check Answer

Option 1

Q.No:42 TIFR-2025

A quantum particle is in the ground state of an infinite potential well of length \(L\) with \[ V(x) = \begin{cases} 0 & \text{for } x \in [0,L] \\ +\infty & \text{otherwise} \end{cases} \] What is the expectation value of the operator \[ \hat{O} = \hat{x}\hat{p} + \hat{p}\hat{x} \] in this state?

1) 0

2)\( i\hbar\)

3) \(\frac{\hbar}{2}\)

4) \(-\,i\hbar\)

Check Answer

Option 1

Q.No:43 TIFR-2025

Consider a quantum particle of mass \(m\) in an infinite one–dimensional potential well of length \(L\) between points A and B. The particle is in the ground state with an energy \(E_{g}\). The wall at B is suddenly shifted to B′ where AB′ has length \(2L\). We measure the energy again and obtain the value \(E_{1}\). What is the probability that \(E_{1} \ne E_{g}\)?

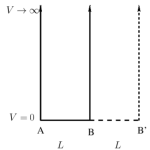
1) \(\frac{1}{2}\)

2) \(\frac{1}{4}\)

3) 1

4) 0

Check Answer

Option 1

Q.No:44 TIFR-2025

A stream of electrons, each having an energy of 0.5 eV, impinges on a pair of extremely thin slits separated by \(10\,\mu\mathrm{m}\). The distance between adjacent minima on a screen \(20\,\mathrm{m}\) behind the slits would be closest to:

1) 3.48 mm

2) 1.74 mm

3) 6.96 cm

4) 5 m

Check Answer

Option 1

Q.No:45 TIFR-2025

Radiation from the Big–Bang observed today has a black–body spectrum with \(T = 2.7\ \mathrm{K}\) and its energy density as a function of the wavelength peaks at \(\lambda = 1.1\ \mathrm{mm}\). This radiation is red–shifted to longer wavelengths compared to the black–body spectrum when the universe was hotter, say at \(270\ \mathrm{K}\). What was the photon energy corresponding to the wavelength at which the energy density peaked, when the universe was at \(270\ \mathrm{K}\)?

1) 0.12 eV

2) 1.2 meV

3) 23 meV

4) 0.23 eV