Q.No:1 TIFR-2012
Consider a sealed but thermally conducting container of total volume \(V\), which is in equilibrium with a thermal bath at temperature \(T\). The container is divided into two equal chambers by a thin but impermeable partition. One of these chambers contains an ideal gas, while the other half is a vacuum (see figure).

If the partition is removed and the ideal gas is allowed to expand and fill the entire container, then the entropy per molecule of the system will increase by an amount
(a)
\(2k_B\)
(b)
\(k_B \ln{(1/2)}\)
(c)
\(k_B \ln{2}\)
(d)
\((k_B \ln{2})/2\)
Check Answer
Option c
Q.No:2 TIFR-2012
When a gas is enclosed in an impermeable box and heated to a high temperature \(T\), some of the neutral atoms lose an electron and become ions. If the number density of neutral atoms, ions and electrons is \(N_a, N_i\) and \(N_e\), respectively, these can be related to the average volume \(V_a\) occupied by an atom/ion and the ionisation energy \(E\) by the relation
(a)
\(N_e(N_a+N_i)=(N_a/V_a)\exp{(-E/k_B T)}\)
(b)
\(N_a(N_e+N_i)=(N_a/V_a)\exp{(-E/k_B T)}\)
(c)
\(N_e N_i=(N_a/V_a)\exp{(+E/k_B T)}\)
(d)
\(N_e N_i=(N_a/V_a)\exp{(-E/k_B T)}\)
Check Answer
Option d
Q.No:3 TIFR-2013
Consider an ensemble of microscopic quantum mechanical systems with two energy levels \(E_1\) and \(E_2\), where \(E_1<E_2\). Which of the following graphs best describes the temperature dependence of the average energy \(\langle E\rangle\) of the system?
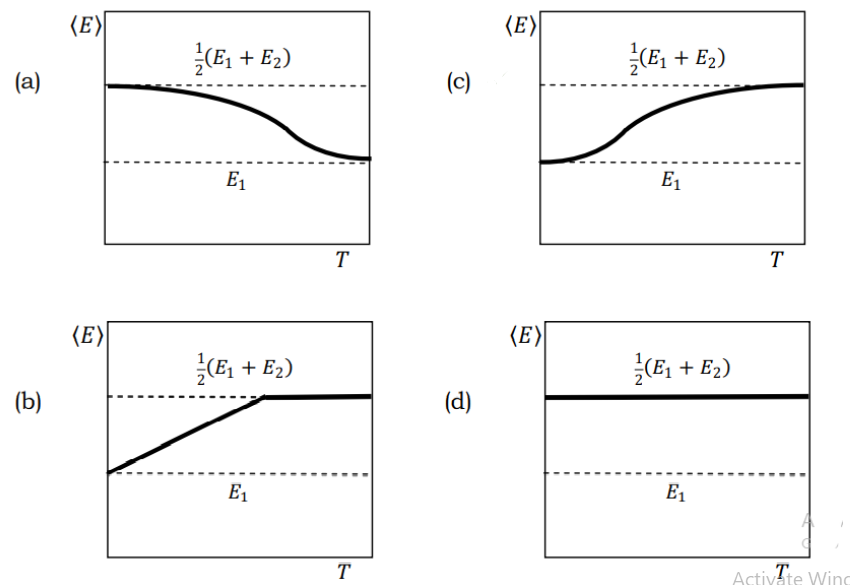
Check Answer
Option c
Q.No:4 TIFR-2013
An system at temperature \(T\) has three energy states \(0, \pm \varepsilon\). The entropy of the system in the low temperature (\(T\to 0\)) and high temperature (\(T\to \infty\)) limits are, respectively,
(a)
\(S_{T\to 0}=0\) and \(S_{T\to \infty}=k_B\exp{(-3)}\)
(b)
\(S_{T\to 0}=S_{T\to \infty}=k_B \ln{3}\)
(c)
\(S_{T\to 0}=0\) and \(S_{T\to \infty}=k_B \ln {3}\)
(d)
\(S_{T\to 0}=0\) and \(S_{T\to \infty}=3k_B/2\)
Check Answer
Option c
Q.No:5 TIFR-2014
Consider the \({CO}\) molecule as a system of two point particles which has both translational and rotational degrees of freedom. Using classical statistical mechanics, the molar specific heat \(C_V\) of \({CO}\) gas is given in terms of the Boltzmann constant \(k_B\) by
(a)
\(\frac{5}{2}k_B\)
(b)
\(2k_B\)
(c)
\(\frac{3}{2}k_B\)
(d)
\(\frac{1}{2}k_B\)
Check Answer
Option a
Q.No:6 TIFR-2015
In a monatomic gas, the first excited state is only \(1.5 eV\) above the ground state, while the other excited states are much higher up. The ground state is doubly-degenerate, while the first excited state has a four-fold degeneracy. If now, the gas is heated to a temperature of \(7000 K\), the fraction of atoms in the excited state will be approximately
(a)
\(0.14\)
(b)
\(0.07\)
(c)
\(0.42\)
(d)
\(0.3\)
Check Answer
Option a
Q.No:7 TIFR-2016
\(N\) distinguishable particles are distributed among three states having eneries \(E=0, k_B T\) and \(2k_B T\) respectively. If the total equilibrium energy of the system is \(138.06 k_B T\), find the number \(N\) of particles.
Check Answer
Ans 325
Q.No:8 TIFR-2017
Consider a system of non-interacting particles with integer angular momentum \(J\) at a temperature \(T\). This system is placed in a magnetic field \(B\) in the \(z\) direction. The energy of a state with \(J_z=m\hbar\) is
\[
E_m=m\mu_B B
\]
with \(\mu_B>0\). The fractional magnetization of the particles as a function of \(\mu_B B/k_B T\) can be represented as

Check Answer
Option a
Q.No:9 TIFR-2017
Two identical bosons may occupy any of two energy levels \(0, \varepsilon\), where \(\varepsilon>0\). The lowest energy state is doubly-degenerate and the excited state is non-degenerate. Assume that the two-particle system is in thermal equilibrium at a temperature \(T\). Calculate the average energy \(\langle E\rangle\). What will be the leading term of
\[
\frac{\langle E\rangle}{\exp{\left(-\frac{\varepsilon}{k_B T}\right)}}
\]
at low temperature?
Check Answer
Ans \(=2\epsilon/3\)
Q.No:10 TIFR-2017
A one-dimensional quantum harmonic oscillator of natural frequency \(\omega\) is in thermal equilibrium with a heat bath at temperature \(T\). The mean value \(\langle E\rangle\) of the energy of the oscillator can be written as
(a)
\(\frac{\hbar \omega}{2}\text{sech}{\left(\frac{\hbar \omega}{2k_B T}\right)}\)
(b)
\(\frac{\hbar \omega}{2}\text{csch}{\left(\frac{\hbar \omega}{2k_B T}\right)}\)
(c)
\(\frac{\hbar \omega}{2}\coth{\left(\frac{\hbar \omega}{2k_B T}\right)}\)
(d)
\(\frac{\hbar \omega}{2}\tanh{\left(\frac{\hbar \omega}{2k_B T}\right)}\)
Check Answer
Option c
Q.No:11 TIFR-2017
Hydrogen atoms in the atmosphere of a star are in thermal equilibrium, with an average kinetic energy of \(1 \hspace{1mm}\text{eV}\). The ratio of the number of hydrogen atoms in the 2nd excited state (\(n=3\)) to the number in the ground state (\(n=1\)) is
(a)
\(3.16\times 10^{-11}\)
(b)
\(1.33\times 10^{-8}\)
(c)
\(3.16\times 10^{-8}\)
(d)
\(5.62\times 10^{-6}\)
Check Answer
Option b
Q.No:12 TIFR-2018
A classical ideal gas of atoms with masses \(m\) is confined in a three-dimensional potential
\[
V(x, y, z)=\frac{\lambda}{2}(x^2+y^2+z^2)
\]
at a temperature \(T\). If \(k_B\) is the Boltzmann constant, the root mean square (r.m.s.) distance of the atoms from the origin is
(a)
\(\left(\frac{3k_B T}{\lambda}\right)^{1/2}\)
(b)
\(\left(\frac{3k_B T}{2\lambda}\right)^{1/2}\)
(c)
\(\left(\frac{2k_B T}{3\lambda}\right)^{1/2}\)
(d)
\(\left(\frac{k_B T}{\lambda}\right)^{1/2}\)
Check Answer
Option a
Q.No:13 TIFR-2018
\(N\) particles are distributed among three energy levels having energies: \(0, k_B T\) and \(2k_B T\) respectively. If the total equilibrium energy of the system is approximately \(42.5 k_B T\) then find the value of \(N\) (to the closest integer).
Check Answer
Ans \(100\)
Q.No:14 TIFR-2018
A statistical system, kept at a temperature \(T\), has \(n\) discrete energy levels with equal level-spacing \(\varepsilon\), starting from energy \(0\). If, now, a single particle is placed in the system what will be the mean energy of the system in the limit as \(n\to \infty\)? [The answer should not be left as a summation]
Check Answer
Ans
Q.No:15 TIFR-2019
Consider the following linear model of a molecule of hydrogen cyanide \((HCN)\) depicted below.

It follows that the molar specific heat of hydrogen cyanide gas at constant pressure must be
(d)
\(6R\)
(d)
\(4.5R\)
(d)
\(5R\)
(d)
\(5.5R\)
Check Answer
Option d
Q.No:16 TIFR-2019
Consider \(N\) non-interacting distinguishable particles in equilibrium at an absolute temperature \(T\). Each particle can only occupy one of two possible states of energy \(0\) and respectively \(\epsilon\) respectively (\(\epsilon>0\)). The entropy of the system, in terms of \(\beta=\epsilon/k_B T\) is
(a)
\(Nk_B\left\{\ln{(1+e^{-\beta})}-\frac{e^{-\beta}}{1+e^{-\beta}}\right\}\)
(b)
\(Nk_B\left\{\ln{(1+e^{-\beta})}+\frac{\beta e^{-\beta}}{1+e^{-\beta}}\right\}\)
(c)
\(Nk_B\left\{\ln{(1-e^{-\beta})}+\frac{\beta e^{-\beta}}{1-e^{-\beta}}\right\}\)
(d)
\(Nk_B\left\{\ln{(1+e^{-\beta})}-\frac{e^{-\beta}}{1-e^{-\beta}}\right\}\)
Check Answer
Option b
Q.No:17 TIFR-2020
In a certain atom, the ground state and first excited state of the valence electron are \(-7.8 \hspace{1mm}\text{eV}\) and \(-3.9 \hspace{1mm}\text{eV}\), while all the higher excited states have energies very close to zero. The ground state has a degeneracy of \(2\), while the first excited state has a degeneracy of \(6\).
It follows that if these atoms reside in the outer layers of a blue giant star at a temperature around \(2.32\times 10^4 \hspace{1mm}\text{K}\), the average energy per atom will be approximately
(a)
\(-5.1 \hspace{1mm}\text{eV}\)
(b)
\(-5.9 \hspace{1mm}\text{eV}\)
(c)
\(-6.8 \hspace{1mm}\text{eV}\)
(d)
\(-4.4 \hspace{1mm}\text{eV}\)
Check Answer
Option c
Q.No:18 TIFR-2020
A square lattice consists of \(2N\) sites, of which alternate sites are labeled A and B. An example with \(N=6\) is shown on the right. Now, \(N\) identical classical particles are distributed over these sites, such that each site can accommodate at most one particle.

The fraction of the total number \(N\) of particles occupying A sites is denoted \(\alpha\) and the fraction occupying B sites is denoted \(\beta\), so that \(\alpha+\beta=1\).
If \(\alpha, \beta\) are fixed and \(N\gg 1\), the entropy \(S\) of the system can be written
(a)
\(S=-2Nk_B T(\alpha\ln{\alpha}+\beta\ln{\beta})\)
(b)
\(S=2Nk_B T(\alpha\ln{\alpha}+\beta\ln{\beta})\)
(c)
\(S=-2Nk_B T(\alpha\ln{\alpha}-\beta\ln{\beta})\)
(d)
\(S=2Nk_B T(\alpha\ln{\alpha}-\beta\ln{\beta})\)
Check Answer
Option a
Q.No:19 TIFR-2020
A system is composed of a large number of non-interacting classical particles moving in two dimensions, which individually obey the Hamiltonian
\[
\frac{p_x^2+p_y^2}{2m}+\frac{1}{2}m\omega^2(x^2+y^2)
\]
and the system is connected to a heat bath at a temperature \(T\).
The probability of finding a particle within a radius \(R\) from the origin is given by
(a)
\(1-\exp{\left(-\frac{m\omega^2 R^2}{2T}\right)}\)
(b)
\(\exp{\left(-\frac{m\omega^2 R^2}{2T}\right)}\)
(c)
\(\text{erf}\left(\sqrt{\frac{m}{2T}}\omega R\right)\)
(d)
\(1-\frac{m\omega^2 R^2}{2T}\)
Check Answer
Option a
Q.No:20 TIFR-2021
Which of the following is the entropy generated when two identical blocks at temperatures \(2T\) and \(T\) are brought into thermal contact and allowed to reach equilibrium?
[Assume that the heat capacity of each block is \(C\)]
(a)
\(C(2\ln{3}-3\ln{2})\)
(b)
zero
(c)
\(2C\ln{\frac{3}{2}}\)
(d)
\(C(2\ln{2}-3\ln{3})\)
Check Answer
Option a
Q.No:21 TIFR-2021
A certain system has one state with energy \(E\), two states with energy \(2E\), three states with energy \(3E\) and so on, where \(E>0\). The partition function \(Z\) of the system at temperature \(T\) is given by
(a)
\(\frac{1}{Z}=4\sinh^2{\frac{E}{2T}}\)
(b)
\(\frac{1}{Z}=2\cosh^2{\frac{E}{4T}}\)
(c)
\(\frac{1}{Z}=4\coth^2{\frac{E}{2T}}\)
(d)
\(\frac{1}{Z}=2\tanh^2{\frac{E}{4T}}\)
Check Answer
Option a
Q.No:22 TIFR-2022
A vertical cylinder of height \(H\) is filled with an ideal gas of classical point particles each of mass \(m\) and is allowed to come to equilibrium under gravity at a temperature \(T\). The mean height of these particles is
(a)
\(\frac{k_B T}{mg} \hspace{2mm} (1-\frac{mgH/k_B T}{e^{mgh/k_B T}-1})\)
(b)
\(\frac{H}{3} \hspace{2mm} \frac{mgH/k_B T}{e^{mgh/k_B T}+1}\)
(c)
\(\frac{k_B T}{mg} \hspace{2mm} (1-\frac{mgH/k_B T}{e^{mgh/k_B T}+1})\)
(d)
\(\frac{H}{3} \hspace{2mm} \frac{mgH/k_B T}{e^{mgh/k_B T}-1}\)
Check Answer
Option a
Q.No:23 TIFR-2023
A two-level system with zero ground state energy is in equilibrium at a nonzero finite temperature. If \(\alpha\) is defined as the ratio
\[\alpha=\frac{\langle E^2 \rangle }{\langle E \rangle ^2}\]
where \(\langle E \rangle\) denotes mean energy and \(\langle E^2 \rangle\) denotes mean squared energy, then
(a)
\(2< \alpha < \infty\)
(b)
\(0< \alpha < \frac{1}{2}\)
(c)
\(\frac{1}{2}< \alpha < 1\)
(d)
\(1< \alpha \leq 2\)
Check Answer
Option a
Q.No:24 TIFR-2024
A collection of \( N \) spin-\(\frac{1}{2}\) objects, with individual energy eigenvalues \(0, E \), are kept at a temperature \( T \). Which of the following curves accurately represent the temperature dependence of specific heat of the system?
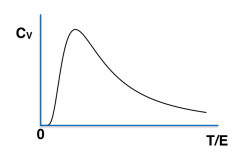


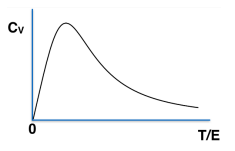
Check Answer
Option a
Q.No:26 TIFR-2024
A string has 8 beads in a row, with \( n \) identical red beads and \( \left(8 - n\right) \) identical blue beads. When one of the red beads is replaced by a blue one, the entropy of the given system changes from \( S \) to \( S + k_B \ln 2 \). All configurations of the beads are equally probable. What is the value of \( n \)?
(a) 6
(b) 2
(c) 4
(d) 8
Check Answer
Option a
Q.No:25 TIFR-2024
Each site of a linear chain of \( N \) sites has a spin which can be in three different states with energies \( 0, \pm \epsilon \), as shown in the figure below.

The system has a constraint that the neighboring spins cannot be in the same state. At infinite temperature, the entropy of the system is given by:
(a) \( N \ln 2 + \ln \frac{3}{2} \)
(b) \( N \ln 3 \)
(c) \( (N - 1) \ln 2 \)
(d) \( N \ln 2 \)
Check Answer
Option a
Q.No:26 TIFR-2025
Consider two ideal gases \(A\) and \(B\) with atomic masses \(m_A\) and \(m_B\)
respectively such that \(m_A > m_B\). The two gases with the same number of moles
are kept at the same temperature and confined in containers with the same volume.
Which of the gases will exert more pressure and molecules of which gas will have
a higher RMS momentum?
a) Both will exert the same pressure but molecules of Gas \(A\) will have more RMS momentum
b) Gas \(A\) will exert more pressure and molecules of Gas \(B\) will have more RMS momentum
c) Gas \(B\) will exert more pressure but molecules of Gas \(A\) will have more RMS momentum
d) Both will exert the same pressure and molecules of both gases have the same RMS momentum
Check Answer
Option a
Q.No:27 TIFR-2025
A classical ideal gas at temperature \(T\) is placed in a spherically symmetric potential
\[
V(r) = c\, r^{3}
\]
What is \(\langle V(r) \rangle\) per particle?
a) \(kT\)
b) \(\frac{3kT}{2}\)
c) \(\frac{kT}{2}\)
d) \(\frac{kT}{3}\)

Q.No.1 Discussion :
Q.No.2 Discussion :
Q.No.3 Discussion :
Option c
Q.No.4 Discussion :
Q.No.5 Discussion :
ans option A
Q.No.6 Discussion :
my solution
Q.No.7 Discussion :
Number of Particles is 325
Q.No.8 Discussion :
Q.No.9 Discussion :
Ans
Q.No.10 Discussion :
Ans
Q.No.11 Discussion :
Ans
Q.No.12 Discussion :
Answer
Q.No.13 Discussion :
Q13 TIFR 2018
Q.No.14 Discussion :
Ans
Q.No.15 Discussion :
Ans
Q.No.16 Discussion :
Ans
Q.No.17 Discussion :
Option C
Q.No.18 Discussion :
Q.No.19 Discussion :
Q.No.20 Discussion :
Answer:
Q.No.21 Discussion :
Solution
Q.No.22 Discussion :
Solution
Q.No.23 Discussion :
Answer: A
Q.No.4
Question 25
Question 26
Q.No.2
Option D