Q.No:1 GATE-2012
The value of the integral \(\oint_C e^{1/z} dz\), using the contour \(C\) of circle with unit radius \(|z|=1\) is
(A)
\(0\)
(B)
\(1-2\pi i\)
(C)
\(1+2\pi i\)
(D)
\(2\pi i\)
Check Answer
Option D
Q.No:2 GATE-2013
For the function \(f(z)=\frac{16z}{(z+3)(z-1)^2}\), the residue at the pole \(z=1\) is (your answer should be an integer) ____________.
Check Answer
Ans 3
Q.No:3 GATE-2014
The value of the integral
\[
\oint_C \frac{z^2}{e^z+1} dz,
\]
where \(C\) is the circle \(|z|=4\), is
(A)
\(2\pi i\)
(B)
\(2\pi^2 i\)
(C)
\(4\pi^3 i\)
(D)
\(4\pi^2 i\)
Check Answer
Option C
Q.No:4 GATE-2015
Consider \(w=f(z)=u(x, y)+iv(x, y)\) to be an analytic function in a domain \(D\). Which one of the following options is \({\bf NOT}\) correct?
(A)
\(u(x, y)\) satisfies Laplace equation in \(D\)
(B)
\(v(x, y)\) satisfies Laplace equation in \(D\)
(C)
\(\int_{z_1}^{z_2} f(z) dz\) is dependent on the choice of the contour between \(z_1\) and \(z_2\) in \(D\)
(D)
\(f(z)\) can be Taylor expanded in \(D\)
Check Answer
Option C
Q.No:5 GATE-2015
Consider a complex function \(f(z)=\frac{1}{z\left(z+\frac{1}{2}\right)\cos{(z\pi)}}\). Which one of the following statements is correct?
(A)
\(f(z)\) has simple poles at \(z=0\) and \(z=-1/2\)
(B)
\(f(z)\) has a second order pole at \(z=-1/2\)
(C)
\(f(z)\) has infinite number of second order poles
(D)
\(f(z)\) has all simple poles
Check Answer
Option B
Q.No:6 GATE-2017
The contour integral \(\oint \frac{dz}{1+z^2}\) evaluated along a contour going from \(-\infty\) to \(+\infty\) along the real axis and closed in the lower half-plane by a half circle is equal to __________. (up to two decimal places).
Check Answer
Ans 3.13-3.15
Q.No:7 GATE-2017
The imaginary part of an analytic complex function is \(\nu(x, y)=2xy+3y\). The real part of the function is zero at the origin. The value of the real part of the function at \(1+i\) is ___________. (up to two decimal places).
Check Answer
Ans 2.90-3.10
Q.No:8 GATE-2019
The absolute value of the integral
\[
\int \frac{5z^3+3z^2}{z^2-4} dz,
\]
over the circle \(|z-1.5|-1\) in complex plane, is _____________ (up to two decimal places).
Check Answer
Ans 81.60-81.80
Q.No:9 GATE-2019
The pole of the function \(f(z)=\cot{z}\) at \(z=0\) is
(A)
a removable singularity
(B)
an essential singularity
(C)
a simple pole
(D)
a second order pole
Check Answer
Option C
Q.No:10 GATE-2019
The value of the integral \(\int_{-\infty}^{\infty} \frac{\cos{(kx)}}{x^2+a^2} dx\), where \(k>0\) and \(a>0\), is
(A)
\(\frac{\pi}{a}e^{-ka}\)
(B)
\(\frac{2\pi}{a}e^{-ka}\)
(C)
\(\frac{\pi}{2a}e^{-ka}\)
(D)
\(\frac{3\pi}{2a}e^{-ka}\)
Check Answer
Option A
Q.No:11 GATE-2020
For a complex variable \(z\) and the contour \(c:|z|=1\) taken in the counter clockwise direction, \(\frac{1}{2\pi i}\oint_C \left(z-\frac{2}{z}+\frac{3}{z^2}\right)dz=\) ______________.
Check Answer
Ans (-2)
Q.No:12 GATE-2021
A contour integral is defined as
\[
I_n=\oint_{C} \frac{dz}{(z-n)^2+\pi^2}
\]
where \(n\) is a positive integer and \(C\) is the closed contour, as shown in the figure, consisting of the line from \(-100\) to \(100\) and the semicircle traversed in the counter-clockwise sense.

The value of \(\sum_{n=1}^{5} I_n\) (in integer) is __________.
Check Answer
Ans 5
Q.No:13 GATE-2022
Complex function \(f(z)=z+|z-a|^2\) (\(a\) is a real number) is
(a)
continuous at \((a, a)\)
(b)
complex-differentiable at \((a, a)\)
(c)
complex-differentiable at \((a, 0)\)
(d)
analytic at \((a, 0)\)
Check Answer
Option a,c
Q.No:14 GATE-2023
Consider two real functions
\[U(x,y)=xy()x^2-y^2,\]
\[V(x,y)=ax^4+by^4+cx^2y^2+k,\]
where \(k\) is a real constant and \(a,b,c\) are real coefficients. If \(U(x,y) +i V(x,y)\) is analytic, then what is the value of \(a\times b\times c\) ?
(A)
\(\frac{1}{8}\)
(B)
\(\frac{3}{28}\)
(C)
\(\frac{5}{36}\)
(D)
\(\frac{3}{32}\)
Check Answer
Option D
Q.No:15 GATE-2023
Consider the complex function
\[f(z)=\frac{z^2 \hspace{0.5mm} sin \hspace{0.5mm} z}{(z-\pi)^4}.\]
At \(z=\pi\) , which of the following options is(are) CORRECT?
(A)
The order of the pole is 4
(B)
The order of the pole is 3
(C)
The residue at the pole is \(\frac{\pi}{6}\)
(D)
The residue at the pole is \(\frac{2\pi}{3}\)
Check Answer
Option B
Q.No:16 GATE-2024
The complex function
\[
e^{-\left(\frac{2}{z-1}\right)}
\]
has
(A) a simple pole at \( z = 1 \)
(B) an essential singularity at \( z = 1 \)
(C) a residue equal to \( -2 \) at \( z = 1 \)
(D) a branch point at \( z = 1 \)
Check Answer
Option B,C
Q.No:17 GATE-2025
Consider the function
\[
f(z) = \frac{1}{z^{2}(z-2)^{3}}
\]
of a complex variable \(z\).
The residues of the function at \(z = 0\) and \(z = 2\), respectively, are
A) \(-\frac{3}{8}\) and \(\frac{3}{8}\)
B) \(\frac{3}{8}\) and \(-\frac{3}{16}\)
C) \(-\frac{3}{16}\) and \(\frac{3}{16}\)
D) \(-\frac{3}{8}\) and \(\frac{3}{16}\)
Check Answer
Option C
Q.No:18 GATE-2025
Consider the integral
\[
I = \frac{1}{2\pi i}\oint \frac{z^{4}-1}{\left(z-\frac{a}{b}\right)\left(z-\frac{b}{a}\right)}\,dz,
\]
where \(z\) is a complex variable and \(a, b\) are positive real numbers.
The integral is taken over the unit circle centered at the origin.
Which of the following option(s) is/are correct?
A) \(I = \frac{5}{8}\) when \(a = 1,\; b = 2\)
B) \(I = \frac{10}{3}\) when \(a = 1,\; b = 3\)
C) \(I = \frac{5}{8}\) when \(a = 2,\; b = 1\)
D) \(I = \frac{5}{8}\) when \(a = 3,\; b = 2\)
Check Answer
Option A,C
Q.No:1 CSIR Dec-2014
The principal value of the integral \(\int_{-\infty}^{\infty} \frac{\sin{(2x)}}{x^3} dx\) is
(1)
\(-2\pi\)
(2)
\(-\pi\)
(3)
\(\pi\)
(4)
\(2\pi\)
Check Answer
Option 1
Q.No:2 CSIR Dec-2014
The Laurent series expansion of the function \(f(z)=e^z+e^{1/z}\) about \(z=0\) is given by
(1)
\(\sum_{n=-\infty}^{\infty} \frac{z^n}{n!}\) for all \(|z|<\infty\)
(2)
\(\sum_{n=0}^{\infty} \left(z^n+\frac{1}{z^n}\right) \frac{1}{n!}\) only if \(0<|z|<1\)
(3)
\(\sum_{n=0}^{\infty} \left(z^n+\frac{1}{z^n}\right) \frac{1}{n!}\) for all \(0<|z|<\infty\)
(4)
\(\sum_{n=-\infty}^{\infty} \frac{z^n}{n!}\), only if \(|z|<1\)
Check Answer
Option 3
Q.No:3 CSIR Dec-2014
Consider the function \(f(z)=\frac{1}{z}\ln{(1-z)}\) of a complex variable \(z=re^{i\theta}\) (\(r\geq 0, -\infty<\theta<\infty\)). The singularities of \(f(z)\) are as follows:
(1)
branch points at \(z=1\) and \(z=\infty\); and a pole at \(z=0\) only for \(0\leq \theta<2\pi\)
(2)
branch points at \(z=1\) and \(z=\infty\); and a pole at \(z=0\) for all \(\theta\) other than \(0\leq \theta<2\pi\)
(3)
branch points at \(z=1\) and \(z=\infty\); and a pole at \(z=0\) for all \(\theta\)
(4)
branch points at \(z=0, z=1\) and \(z=\infty\).
Check Answer
Option 2
Q.No:4 CSIR June-2015
The value of the integral \(\int^{\infty}_{- \infty}\frac{dx}{1 +x^4}\) is
(1)
\(\frac{\pi}{\sqrt{2}}\)
(2)
\(\frac{\pi}{2}\)
(3)
\(\sqrt{2}{\pi}\)
(4)
\(2 {\pi}\)
Check Answer
Option 1
Q.No:5 CSIR Dec-2015
The function \(\frac{z}{\sin{\pi z^2}}\) of a complex variable \(z\) has
(1)
a simple pole at \(0\) and poles of order \(2\) at \(\pm \sqrt{n}\) for \(n=1, 2, 3 \cdots\)
(2)
a simple pole at \(0\) and poles of order \(2\) at \(\pm \sqrt{n}\) and \(\pm i\sqrt{n}\) for \(n=1, 2, 3 \cdots\)
(3)
poles of order \(2\) at \(\pm \sqrt{n}\), \(n=0, 1, 2, 3 \cdots\)
(4)
poles of order \(2\) at \(\pm n\), \(n=0, 1, 2, 3 \cdots\)
Check Answer
Option 2
Q.No:6 CSIR June-2016
The value of the contour integral
\[
\frac{1}{2\pi i}\oint_C \frac{e^{4z}-1}{\cosh{(z)}-2\sinh{(z)}} dz
\]
around the unit circle \(C\) traversed in the anti-clockwise direction, is
(1)
\(0\)
(2)
\(2\)
(3)
\(-8/\sqrt{3}\)
(4)
\(-\tanh{\left(\frac{1}{2}\right)}\)
Check Answer
Option 3
Q.No:7 CSIR Dec-2016
The Fourier transform \(\int_{-\infty}^{\infty} dx f(x) e^{ikx}\) of the function \(f(x)=\frac{1}{x^2+2}\) is
(1)
\(\sqrt{2}\pi e^{-\sqrt{2}|k|}\)
(2)
\(\sqrt{2}\pi e^{-\sqrt{2}k}\)
(3)
\(\frac{\pi}{\sqrt{2}} e^{-\sqrt{2}k}\)
(4)
\(\frac{\pi}{\sqrt{2}} e^{-\sqrt{2}|k|}\)
Check Answer
Option 4
Q.No:8 CSIR June-2017
The integral \(\oint_{\Gamma} \frac{ze^{i\pi z/2}}{z^2-1} dz\) along the closed contour \(\Gamma\) shown in the figure is
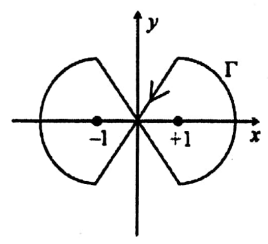
(1)
\(0\)
(2)
\(2\pi\)
(3)
\(-2\pi\)
(4)
\(4\pi i\)
Check Answer
Option 3
Q.No:9 CSIR June-2017
Let \(u(x, y)=e^{ax}\cos{(by)}\) be the real part of a function \(f(z)=u(x, y)+iv(x, y)\) of the complex variable \(z=x+iy\), where \(a, b\) are real constants and \(a\neq 0\). The function \(f(z)\) is complex analytic everywhere in the complex plane if and only if
(1)
\(b=0\)
(2)
\(b=\pm a\)
(3)
\(b=\pm 2\pi a\)
(4)
\(b=a\pm 2\pi\)
Check Answer
Option 2
Q.No:10 CSIR June-2018
What is the value of \(\alpha\) for which \(f(x, y)=2x+3(x^2-y^2)+2i(3xy+\alpha y)\) is an analytic function of complex variable \(z=x+iy\)?
(1)
\(1\)
(2)
\(0\)
(3)
\(3\)
(4)
\(2\)
Check Answer
Option 1
Q.No:11 CSIR Dec-2018
The value of the integral \(\oint_C \frac{dz}{z} \frac{\tanh{2z}}{\sin{\pi z}}\), where \(C\) is a circle of radius \(\frac{\pi}{2}\), traversed counter-clockwise, with centre at \(z=0\), is
(1)
\(4\)
(2)
\(4i\)
(3)
\(2i\)
(4)
\(0\)
Check Answer
Option 2
Q.No:12 CSIR Dec-2018
The integral \(I=\int_{C} e^z dz\) is evaluated from the point \((-1,0)\) to \((1,0)\) along the contour \(C\), which is an arc of the parabola \(y=x^2-1\), as shown in the figure.

The value of \(I\) is
(1)
\(0\)
(2)
\(2\sinh{1}\)
(3)
\(e^{2i}\sinh{1}\)
(4)
\(e+e^{-1}\)
Check Answer
Option 2
Q.No:13 CSIR Dec-2018
The contour \(C\) of the following integral
\[
\oint_{C} dz \frac{\sqrt{(z-1)(z-3)}}{(z^2-25)^3},
\]
in the complex \(z\)-plane is shown in the figure below.

This integral is equivalent to an integral along the contours

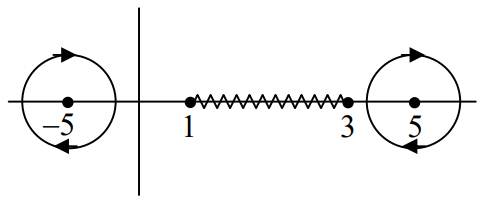


Check Answer
Option 2
Q.No:14 CSIR June-2019
The value of the definite integral \(\int_{0}^{\pi} \frac{d\theta}{5+4\cos{\theta}}\) is
(1)
\(4\pi/3\)
(2)
\(2\pi/3\)
(3)
\(\pi\)
(4)
\(\pi/3\)
Check Answer
Option 4
Q.No:15 CSIR Dec-2019
Let \(C\) be the circle of radius \(\pi/4\), centered at \(z=\frac{1}{4}\) in the complex \(z\)-plane that is traversed counter-clockwise. The value of the contour integral \(\oint_{C} \frac{z^2}{\sin^2{4z}} dz\) is
(1)
\(0\)
(2)
\(\frac{i\pi^2}{4}\)
(3)
\(\frac{i\pi^2}{16}\)
(4)
\(\frac{i\pi}{4}\)
Check Answer
Option 3
Q.No:16 Assam CSIR Dec-2019
The value of the integral \(\frac{1}{2\pi i}\oint_{C} \frac{z}{\sin{z}} dz\), where \(C\) is the contour as shown in the figure below, is

(1)
\(+\pi\)
(2)
\(-\pi\)
(3)
\(-i\pi\)
(4)
\(i\pi\)
Check Answer
Option 1
Q.No:17 Assam CSIR Dec-2019
Three domains \(D_1, D_2\) and \(D_3\) of the complex \(z\)-plane are shown in the figure below.

The Laurent series \(\sum_{n=2}^{\infty} \frac{(-1)^n}{(z-1)^n}=\frac{1}{(z-1)^2}-\frac{1}{(z-1)^3}+\frac{1}{(z-1)^4}-\cdots\) converges to the complex function \(f(z)=\frac{1}{z(z-1)}\) in the
(1)
domain \(D_2\), but not in \(D_3\)
(2)
domain \(D_1\), but not in \(D_2\)
(3)
domains \(D_2\) and \(D_3\)
(4)
domains \(D_1\) and \(D_3\)
Check Answer
Option 3
Q.No:18 CSIR June-2020
A function of a complex variable \(z\) is defined by the integral \(f(z)=\oint_{\Gamma} \frac{w^2-2}{w-z} dw\), where \(\Gamma\) is a circular contour of radius \(3\), centred at origin, running counter-clockwise in the \(w\)-plane. The value of the function at \(z=(2-i)\) is
(a)
\(0\)
(b)
\(1-4i\)
(c)
\(8\pi+2\pi i\)
(d)
\(-\frac{2}{\pi}-\frac{i}{2\pi}\)
Check Answer
Option c
Q.No:19 CSIR Sep-2022
If \(z=i^{i^{i^{.^{.}}}}\) (note that the exponent continuous indefinitely), then a possible value of \(\frac{1}{z}\) ln \(z\) is
(1)
2i ln i
(2)
ln i
(3)
i ln i
(4)
2 ln i
Check Answer
Option 2
Q.No:20 CSIR Sep-2022
At \(z=0\),the function \(\frac{1}{z- sin \hspace{1mm}z}\) of a complex variable \(z\) has
(1)
no singularity
(2)
a simple pole
(3)
a pole of order 2
(4)
a pole of order 3
Check Answer
Option 4
Q.No:21 CSIR Sep-2022
The value of the integral
\[\int_{-\infty}^{\infty} \frac{\cos{(ax)}}{x^2+1} dx
\]
for \(a > 0 \)
(1)
\(\pi e^\alpha\)
(2)
\(\pi e^{-\alpha}\)
(3)
\(\pi e^{-\alpha/2}\)
(4)
\(\pi e^{\alpha/2}\)
Check Answer
Option 2
Q.No:22 CSIR June-2023
The locus of the curve \(Im(\frac{\pi (z-1)-1}{z-1})=1\) in the complex z-plane is a circle centred at (\(x_0,y_0\)) and radius \(R\). The values of (\(x_0,y_0\)) and \(R\), respectively, are
1) \((1,\frac{1}{2})\) and \(\frac{1}{2}\)
2) \((1,-\frac{1}{2})\) and \(\frac{1}{2}\)
3) \((1,1)\) and 1
4) \((1,-1)\) and 1
Check Answer
Option 1
Q.No:23 CSIR Dce-2023
If \( z \) is a complex number, which among the following sets is neither open nor closed?
1)\(\{z \mid 0 \leq |z - 1| \leq 2\}\)
2) \(\{z \mid |z| \leq 1\}\)
3) \(\{z \mid z \in (\mathbb{C} - \{3\}) \text{ and } |z| \leq 100\}\)
4) \(\left\{ z \mid z = r e^{i\theta}, 0 \leq \theta \leq \frac{\pi}{4} \right\}\)
Check Answer
Option 3
Q.No:24 CSIR Dce-2023
The function \( f(z) = \frac{1}{(z+1)(z+3)} \) is defined on the complex plane. The coefficient of the \( (z - z_0)^2 \) term of the Laurent series of \( f(z) \) about \( z_0 = 1 \) is
1) \(\frac{7}{64}\)
2) \(\frac{7}{128}\)
3) \(\frac{9}{64}\)
4) \(\frac{9}{128}\)
Check Answer
Option 2
Q.No:25 CSIR June-2024
The branch line for the function \( f(z) \) is \( \sqrt{\frac{z^2-5z+6}{z^2+2z+1}} \)

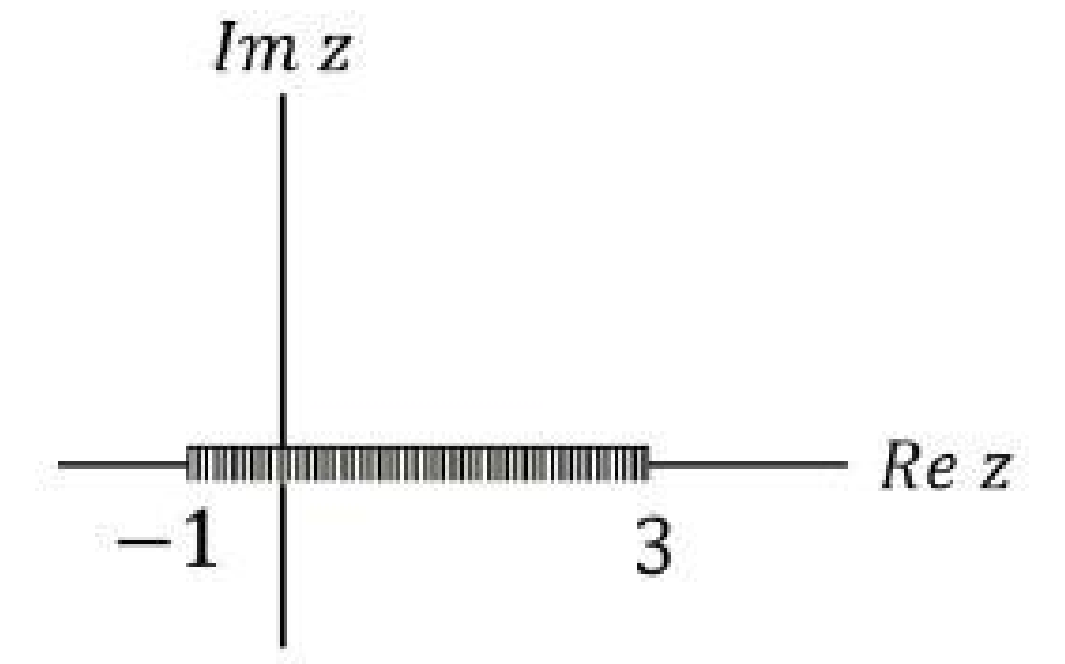
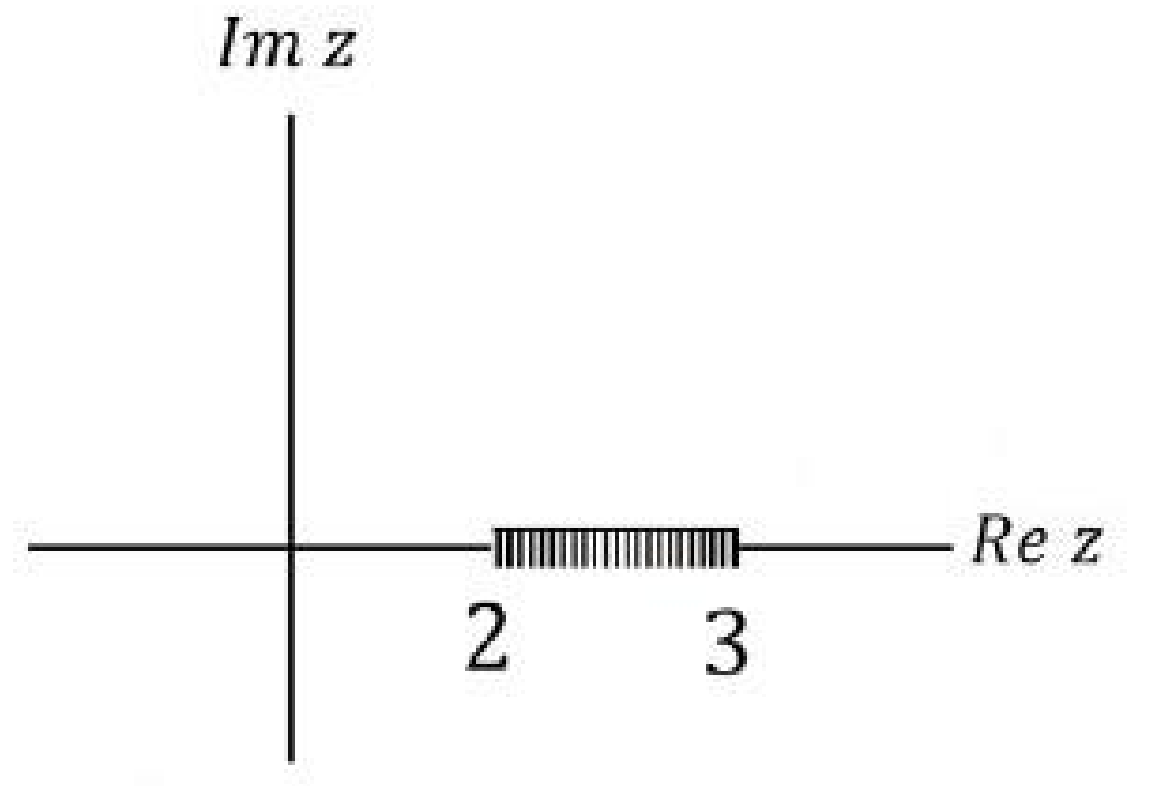
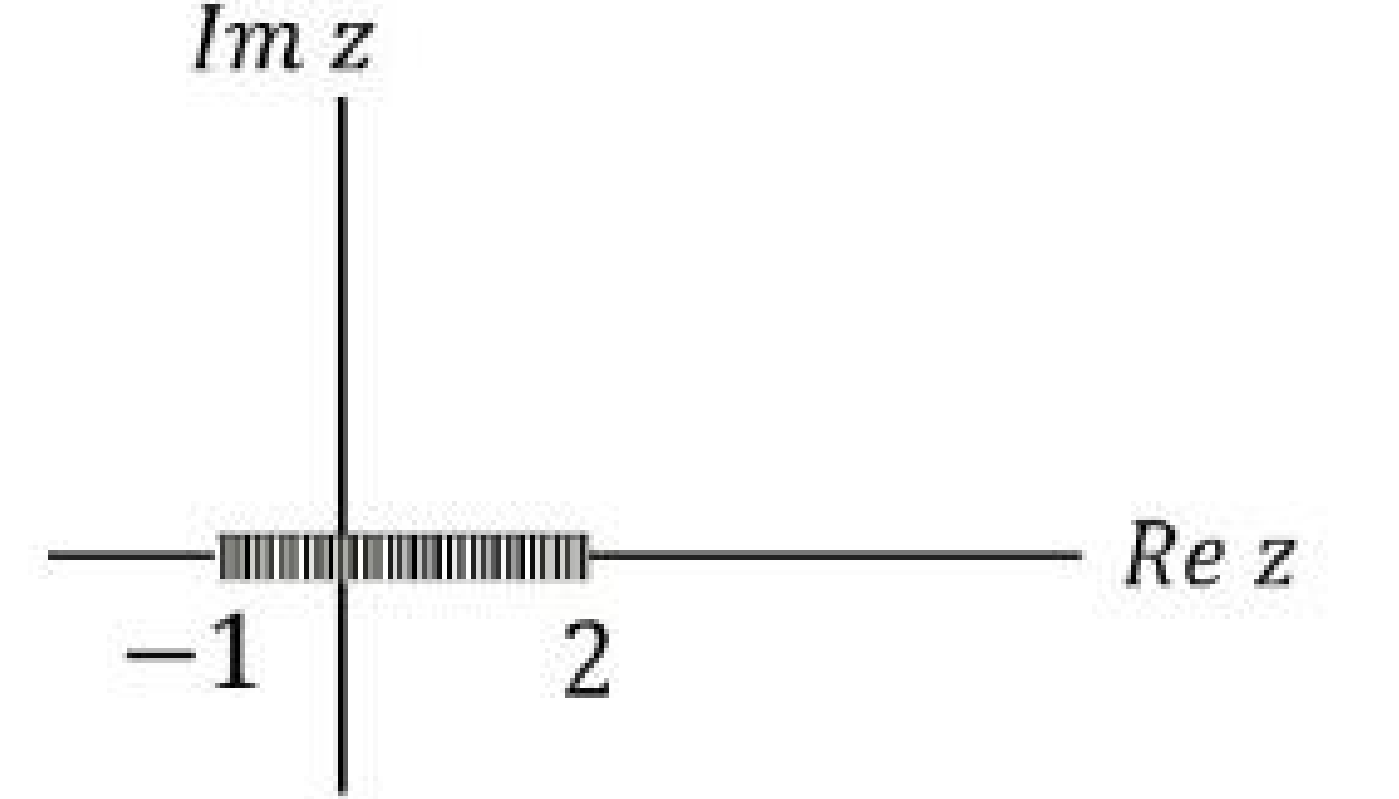
Check Answer
Option 3
Q.No:26 CSIR Dec-2024
The value of the integral (where \(k\) is a constant),
\[
\frac{1}{2\pi i}\oint_C \frac{5}{(z-2)^2}\,\sin(kz)\,dz,
\]
over the closed contour \(C\) shown in the figure, is

1) \( 5k \cos(2k) \)
2) \( 5k \sin(2k) \)
3) \( 5 \cos(2k) \)
4) \( -5k^2 \sin(2k) \)
Check Answer
Option 1
Q.No:27 CSIR Dec-2024
The Gamma function with argument \(z\) is defined as
\[
\Gamma(z) = \int_{0}^{\infty} t^{z-1} e^{-t}\,dt,
\]
where \(z\) is a complex variable and \(\Re(z) \ge 0\).
The function \(\Gamma(z)\) has
1) a branch point at \(z = 0\)
2) a simple pole at \(z = 0\)
3) a removable singularity at \(z = 0\)
4) an essential singularity at \(z = 0\)
Check Answer
Option 2
Q.No:28 CSIR Dec-2024
The complex integral
\[
\oint_C z^4 \exp\!\left(\frac{1}{2z}\right)\,dz,
\]
where \(C\) is the unit circle centered at the origin traversed counter-clockwise, equals
1) \(\frac{\pi i}{120}\)
2) \(\frac{\pi i}{960}\)
3) \(0\)
4) \(\frac{\pi i}{1920}\)
Check Answer
Option 4
Q.No:29 CSIR June-2025
For the function
\[
f(z) = \exp\!\left[z - 1 + \frac{1}{z - 1}\right],
\]
which of the following statements is correct?
1) \(z = 1\) is a pole of order one.
2) \(z = 1\) is an essential singularity.
3) \(z = 1\) is a pole of order two.
4) \(z = 1\) is a removable singular point.
Check Answer
Option 2
Q.No:30 CSIR June-2025
The value of the integral
\[
\int_{0}^{\infty} \frac{\cos(ax)}{1 + x^{2}} \, dx,
\]
where \(a\) is a positive real number, is
1) \(\frac{\pi}{2} e^{-a}\)
2) \(\pi e^{-a}\)
3) \(\frac{\pi}{2} e^{-a/2}\)
4) \(\pi e^{-a/2}\)
