Q.No:1 JEST-2012
The value of the integral \(\int_{0}^{\infty} \frac{\ln{x}}{(x^2+1)^2} dx\) is
(a)
\(0\)
(b)
\(-\pi/4\)
(c)
\(\pi/2\)
(d)
\(-\pi/2\)
Check Answer
Option b
Q.No:2 JEST-2013
Compute
\[
\lim_{z\to 0} \frac{\text{Re}(z^2)+\text{Im}(z^2)}{z^2}.
\]
(a)
The limit does not exist.
(b)
\(1\)
(c)
\(-i\)
(d)
\(-1\)
Check Answer
Option a
Q.No:3 JEST-2014
The value of limit
\[
\lim_{z\to i}\frac{z^{10}+1}{z^6+1}
\]
is equal to
(a)
\(1\)
(b)
\(0\)
(c)
\(-10/3\)
(d)
\(5/3\)
Check Answer
Option d
Q.No:4 JEST-2014
The value of integral
\[
I=\oint_c \frac{\sin{z}}{2z-\pi} dz
\]
with \(c\) a circle \(|z|=2\), is
(a)
\(0\)
(b)
\(2\pi i\)
(c)
\(\pi i\)
(d)
\(-\pi i\)
Check Answer
Option c
Q.No:5 JEST-2015
Given an analytic function \(f(z)=\phi(x, y)+i\psi(x, y)\), where \(\phi(x, y)=x^2+4x-y^2+2y\). If \(C\) is a constant, which of the following relations is true?
(a)
\(\psi(x, y)=x^2 y+4y+C\)
(b)
\(\psi(x, y)=2xy-2x+C\)
(c)
\(\psi(x, y)=2xy+4y-2x+C\)
(d)
\(\psi(x, y)=x^2 y-2x+C\)
Check Answer
Option c
Q.No:6 JEST-2016
The value of the integral \(\int_{0}^{\infty} \frac{\ln{x}}{(x^2+1)}dx\) is:
(A)
\(\pi^2/4\)
(B)
\(\pi^2/2\)
(C)
\(\pi^2\)
(D)
\(0\)
Check Answer
Option D
Q.No:7 JEST-2017
Which one is the image of the complex domain \(\{z\mid xy\geq 1, x+y>0\}\) under the mapping \(f(z)=z^2\), if \(z=x+iy\)?
(A)
\(\{x\mid xy\geq 1, x+y>0\}\)
(B)
\(\{z\mid x\geq 2, x+y>0\}\)
(C)
\(\{z\mid y\geq 2\forall x\}\)
(D)
\(\{z\mid y\geq 1\forall x\}\)
Check Answer
Option C
Q.No:8 JEST-2017
The integral \(I=\int_{1}^{\infty} \frac{\sqrt{x-1}}{(1+x)^2}dx\) is
(A)
\(\frac{\pi}{\sqrt{2}}\).
(B)
\(\frac{\pi}{2\sqrt{2}}\).
(C)
\(\frac{\sqrt{\pi}}{2}\).
(D)
\(\sqrt{\frac{\pi}{2}}\).
Check Answer
Option B
Q.No:9 JEST-2018
The integral
\[
\int_{-\infty}^{\infty} \frac{\cos{x}}{x^2+1}dx
\]
is
(A)
\(\pi/e\)
(B)
\(\pi e^{-2}\)
(C)
\(\pi\)
(D)
zero
Check Answer
Option A
Q.No:10 JEST-2019
Consider the function \(f(x, y)=|x|-i|y|\). In which domain of the complex plane is this function analytic?
(A)
First and second quadrants
(B)
Second and third quadrants
(C)
Second and fourth quadrants
(D)
Nowhere
Check Answer
Option C
Q.No:11 JEST-2020
What is the value of the following contour integral \(I\) taken counterclockwise around the circle \(|z|=2\)?\[
I=\oint_C \frac{dz}{z^3(z+4)}
\]
(A)
\(\frac{\pi i}{2}\)
(B)
\(\frac{\pi i}{32}\)
(C)
\(\frac{\pi i}{16}\)
(D)
\(\frac{\pi i}{4}\)
Check Answer
Option B
Q.No:12 JEST-2022
Consider a complex function
\[
f(z)=\frac{1}{6z^3+3z^2+2z+1}.
\]
What is the sum of the residues at its poles?
(a)
\(0\)
(b)
\(\frac{4}{7}\)
(c)
\(\frac{2}{7}\)
(d)
\(\frac{i\sqrt{3}}{7}\)
Check Answer
Option a
Q.No:13 JEST-2022
Consider a complex number \(z=x+iy\). Where do all the zeros of \(\cos{(z)}\) lie?
(a)
On the \(y=0\) line.
(b)
On the \(x=0\) line.
(c)
On the \(x=y\) line.
(d)
On the \(x=-y\) line.
Check Answer
Option a
Q.No:14 JEST-2023
Calculate the contour integral
\[I=\oint_C \frac{cos^2 (z)-z^2}{(z-a)^3} dz\]
where the clockwise contour \(C\) is encircling the point \(z = a\) in the complex plane.
(a) \(-(sin \hspace{1mm} 2a+1) 2\pi i\)
(b) \(-(cos \hspace{1mm} 2a+1) 2\pi i\)
(c)\((cos \hspace{1mm} 2a+1) 2\pi i\)
(d) \((sin \hspace{1mm} 2a+1) 2\pi i\)
Check Answer
Option c
Q.No:15 JEST-2023
Compute the contour integral:
\[I=\oint \frac{z dz}{sinh (2 \pi z)}\]
where the contour is a circle of radius \(\frac{3}{4}\) centred around the origin and the direction is counterclockwise
(a) \(0\)
(b) \(-1\)
(c) \(\pi\)
(d) \(1\)
Check Answer
Option a
Q.No:16 JEST-2024
What is the value of the integral
\[ \int_{0}^{\infty} \frac{dx}{1 + x^3}? \]
(a) \( \frac{2\pi}{3\sqrt{3}} \)
(b) \( \frac{\pi}{3\sqrt{3}} \)
(c) \( \frac{2\pi}{\sqrt{3}} \)
(d) \( \frac{\pi}{3} \)
Check Answer
Option a
Q.No:17 JEST-2025
What is the value of the integral
\[
I = \frac{3}{2\pi i}\oint_C \frac{dz}{1+z^2},
\]
where the contour \(C\) is a circle of radius \(2\) centered at the origin?
Check Answer
ANS 0
Q.No:1 TIFR-2012
Consider the integral
\[
\int_{-p^2}^{+p^2} \frac{dx}{\sqrt{x^2-p^2}}
\]
where \(p\) is a constant. This integral has a real, nonsingular value if
(a)
\(p<-1\)
(b)
\(p>1\)
(c)
\(p=1\)
(d)
\(p\to 0\)
(e)
\(p\to \infty\)
Check Answer
Option d
Q.No:2 TIFR-2013
If \(z=x+iy\) then the function
\[
f(x, y)=(1+x+y)(1+x-y)+a(x^2-y^2)-1+2iy(1-x-ax)
\]
where \(a\) is a real parameter, is analytic in the complex \(z\) plane if \(a=\)
(a)
\(-1\)
(b)
\(+1\)
(c)
\(0\)
(d)
\(i\)
Check Answer
Option a
Q.No:3 TIFR-2014
The integral
\[
\int_0^{\infty} \frac{dx}{4+x^4}
\]
evaluates to
(a)
\(\pi\)
(b)
\(\frac{\pi}{2}\)
(c)
\(\frac{\pi}{4}\)
(d)
\(\frac{\pi}{8}\)
Check Answer
Option d
Q.No:4 TIFR-2015
The integral
\[
\int_{0}^{2\pi} \frac{d\theta}{1-2a\cos{\theta}+a^2}
\]
where \(0<a<1\), evaluates to
(a)
\(2\pi\)
(b)
\(\frac{2\pi}{1+a^2}\)
(c)
\(\frac{2\pi}{1-a^2}\)
(d)
\(\frac{4\pi}{1-a^2}\)
Check Answer
Option c
Q.No:5 TIFR-2016
The value of the integral
\[
\oint_C \frac{\sin{z}}{z^6} dz
\]
where \(C\) is the circle of centre \(z=0\) and radius \(=1\)
(a)
\(i\pi\)
(b)
\(i\pi/120\)
(c)
\(i\pi/60\)
(d)
\(-i\pi/6\)
Check Answer
Option c
Q.No:6 TIFR-2017
The value of the integral
\[
\int_0^{\infty} \frac{dx}{x^4+4}
\]
Is
(a)
\(\pi\)
(b)
\(\frac{\pi}{2}\)
(c)
\(\frac{\pi}{4}\)
(d)
\(\frac{\pi}{8}\)
Check Answer
Option d
Q.No:7 TIFR-2018
The value of the integral
\[
\frac{1}{\pi}\int_{-\infty}^{\infty} \frac{\cos{x}}{x^2+a^2}
\]
is
(a)
\(1/2a\)
(b)
\(1/2\pi a\)
(c)
\(\pi a\exp{(-a)}\)
(d)
\(\exp{(-a)}/a\)
Check Answer
Option d
Q.No:8 TIFR-2019
Consider the complex function
\[
f(x, y)=u(x, y)+i\nu(x, y)
\]
where
\[
\begin{array}{lll}
u(x, y) &=& x^2(2+x)-y^2(2+3x) \\
\nu(x, y) &=& y(\lambda x+3x^2-y^2)
\end{array}
\]
and \(\lambda\) is real. If it is known that \(f(x, y)\) is analytic in the complex plane of \(z=x+iy\), then it can be written
(a)
\(f=z^2(2+z)\)
(b)
\(f=\bar{z}(2+\bar{z}^2)\)
(c)
\(f=2z\bar{z}+z^2-\bar{z}^2\)
(d)
\(f=z^2+z^3\)
Check Answer
Option a
Q.No:9 TIFR-2020
The value of the integral
\[
\int_0^{\infty} \frac{dx}{x^4+4}
\]
is
(a)
\(\frac{\pi}{8}\)
(b)
\(\frac{3\pi}{8}\)
(c)
\(2\pi\)
(d)
\(\frac{\pi}{4}\)
Check Answer
Option a
Q.No:10 TIFR-2021
How many distinct values can the following function take at a given value of \(z\)?
\[
f(z)=\sqrt{\frac{z^2-1}{\sqrt{z}}}(z-i)^{1/3}
\]
(a)
\(12\)
(b)
\(3\)
(c)
\(4\)
(d)
\(24\)
Check Answer
Option a
Q.No:11 TIFR-2023
A complex analytic function \(\omega=f(z)\) transforms an equilateral triangle in the complex z-plane to another equilateral triangle in the complex \(\omega\)-plane as shown in the figure.
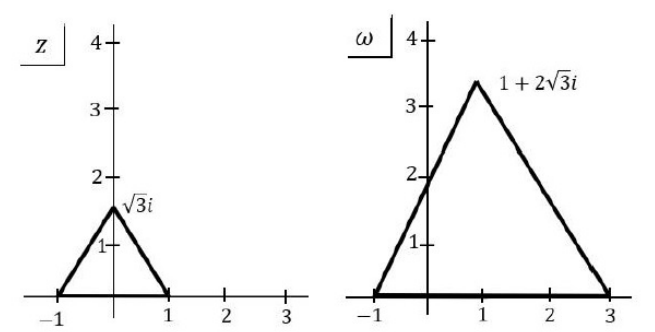
Which one of the options below \(\textbf{CANNOT}\) be \(f(z)\)?
(a)
\(f(z)=2z+1\)
(b)
\(f(z)=e^{5\pi i/6}z+2i\sqrt{3}\)
(c)
\(f(z)=2e^{2\pi i/3}z+2+i\sqrt{3}\)
(d)
\(f(z)=2 i e^{5\pi i/6}z+i\sqrt{3}\)
Check Answer
Option d
Q.No:12 TIFR-2025
(NB: Due to an ambiguity in the question all test takers will be awarded the full score.)
Evaluate the integral
\[
\int_{-\infty}^{+\infty} \frac{e^{-ikx}}{k^2 + 1}\, dk .
\]
a) \(\pi e^{-x}\)
b) \(\pi e^{x}\)
c) \(-\pi e^{-x}\)
d) \(-\pi e^{x}\)

14.Jest 2023 solution: happy solving🤗