Q.No:1 JEST-2012
A beam of X-rays is incident on a BCC crystal. If the difference between the incident and the scattered wavevectors is \(\vec{K}=h\hat{x}+k\hat{y}+l\hat{z}\) where \(\hat{x}, \hat{y}, \hat{z}\) are the unit vectors of the associated cubic lattice, the necessary condition for the scattered beam to give a Laue maximum is
(a)
\(h+k+l=\text{even}\)
(b)
\(h=k=l\)
(c)
\(h, k, l\) are all distinct
(d)
\(h+k+l=\text{odd}\)
Check Answer
Option a
Q.No:2 JEST-2012
The second order maximum in the diffraction of X-rays of \(0.20\) nanometer wavelength from a simple cubic crystal is found to occur at an angle of thirty degrees with respect to the crystal plane. The distance between the lattice planes is
(a)
\(1\) Angstrom
(b)
\(2\) Angstrom
(c)
\(4\) Angstrom
(d)
\(8\) Angstrom
Check Answer
Option c
Q.No:3 JEST-2013
A flat surface is covered with non-overlapping disks of same size. What is the largest fraction of the area that can be covered?
(a)
\(\frac{3}{\pi}\)
(b)
\(\frac{5\pi}{6}\)
(c)
\(\frac{6}{7}\)
(d)
\(\frac{\pi}{2\sqrt{3}}\)
Check Answer
Option d
Q.No:4 JEST-2013
A metal suffers a structural phase transition from face-centred cubic (FCC) to the simple cubic (SC) structure. It is observed that this phase transition does not involve any change of volume. The nearest neighbour distances \(d_{fc}\) and \(d_{sc}\) for the FCC and the SC structures respectively are in the ratio \((d_{fc}/d_{sc})\) [Given \(2^{1/3}=1.26\)]
(a)
\(1.029\)
(b)
\(1.122\)
(c)
\(1.374\)
(d)
\(1.130\)
Check Answer
Option b
Q.No:5 JEST-2014
Circular discs of radius \(1 m\) each are placed on a plane so as to form a closely packed triangular lattice. The number of discs per unit area is approximately equal to
(a)
\(0.86 m^{-2}\)
(b)
\(0.43 m^{-2}\)
(c)
\(0.29 m^{-2}\)
(d)
\(0.14 m^{-2}\)
Check Answer
Option c
Q.No:6 JEST-2015
What is the area of the irreducible Brillouin zone of the crystal structure as given in the figure?

(a)
\(\frac{2\pi^2}{\sqrt{3}A^2}\)
(b)
\(\frac{\sqrt{3}\pi^2}{2A^2}\)
(c)
\(\frac{2\pi^2}{A^2}\)
(d)
\(\frac{\pi^2}{\sqrt{3}A^2}\)
Check Answer
Option a
Q.No:7 JEST-2015
For a \(2\)-dimensional honeycomb lattice as shown in the figure 3, the first Bragg spot occurs for the grazing angle \(\theta_1\) while sweeping the angle from \(0^{\circ}\). The next Bragg spot is obtained at \(\theta_2\) given by

(a)
\(\sin^{-1}{\left(3\sin{\theta_1}\right)}\)
(b)
\(\sin^{-1}{\left(\frac{3}{2}\sin{\theta_1}\right)}\)
(c)
\(\sin^{-1}{\left(\frac{\sqrt{3}}{2}\sin{\theta_1}\right)}\)
(d)
\(\sin^{-1}{\left(\sqrt{3}\sin{\theta_1}\right)}\)
Check Answer
Option c
Q.No:8 JEST-2015
The total number of \({Na^{+}}\) and \({Cl^{-}}\) ions per unit cell of \({Na Cl}\) is,
(a)
\(2\)
(b)
\(4\)
(c)
\(6\)
(d)
\(8\)
Check Answer
Option d
Q.No:9 JEST-2016
If \(\vec{k}\) is the wavevector of incident light (\(|\vec{k}|=2\pi/\lambda\), \(\lambda\) is the wavelength of light) and \(\vec{G}\) is a reciprocal lattice vector, then the Bragg's law can be written as:
(A)
\(\vec{k}+\vec{G}=0\)
(B)
\(2\vec{k}\cdot \vec{G}+G^2=0\)
(C)
\(2\vec{k}\cdot \vec{G}+k^2=0\)
(D)
\(\vec{k}\cdot \vec{G}=0\)
Check Answer
Option B
Q.No:10 JEST-2016
The number of different Bravais lattices possible in two dimensions is:
(A)
\(2\)
(B)
\(3\)
(C)
\(5\)
(D)
\(6\)
Check Answer
Option C
Q.No:1 TIFR-2012
A monochromatic beam of X-rays with wavelength \(\lambda\) is incident at an angle \(\theta\) on a crystal with lattice spacings \(a\) and \(b\) as sketched in the figure below.

A condition for there to be a maximum in the diffracted X-ray intensity is
(a)
\(2\sqrt{a^2+b^2}\sin{\theta}=\lambda\)
(b)
\(2b\cos{\theta}=\lambda\)
(c)
\(2a\cos{\theta}=\lambda\)
(d)
\((a+b)\sin{\theta}=\lambda\)
Check Answer
Option c
Q.No:2 TIFR-2012
Metallic Copper is known to form cubic crystals and the lattice constant is measured from X-ray diffraction studies to be about \(0.36 nm\). If the specific gravity of Copper is \(8.96\) and its atomic weight is \(63.5\), one can conclude that
(a)
the crystals are of simple cubic type
(b)
the crystals are of b.c.c. type
(c)
the crystals are of f.c.c. type
(d)
the crystals are a mixture of f.c.c. and b.c.c. types
(e)
there is insufficient data to distinguish between the previous options
Check Answer
Option c
Q.No:3 TIFR-2016
In a simple cubic lattice of lattice constant \(0.287 nm\), the number of atoms per \(mm^2\) along the \(111\) plane is
(a)
\(2.11\times 10^{13}\)
(b)
\(1.73\times 10^{13}\)
(c)
\(1.29\times 10^{13}\)
(d)
\(1.21\times 10^{13}\)
Check Answer
Option a
Q.No:4 TIFR-2020
A beam of X-rays is incident upon a powder sample of a material which forms simple cubic crystals of lattice constant \(5.5\) Angstrom. The maximum wavelength of the X-rays which can produce diffraction from the planes with Miller indices \((0, 0, 5)\) is
(a)
\(2.2\) Angstrom
(b)
\(55.0\) Angstrom
(c)
\(1.1\) Angstrom
(d)
\(27.5\) Angstrom
Check Answer
Option a
Q.No:5 TIFR-2021
The pictures below are intended to denote a two-dimensional lattice with primitive vectors indicated by arrows and with the unit cell shaded. Which of the following pictures is correct?
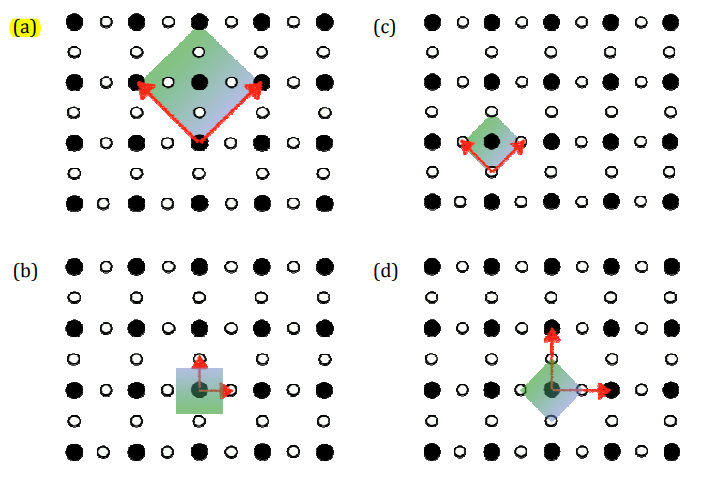
Check Answer
Option a
Q.No:6 TIFR-2024
An X-ray of wavelength 3.1 Å incident on the (110) plane of a cubic lattice with lattice constant \( a \) produces a second-order Bragg reflection at \( \theta = 30^\circ \) (\( \theta \) is the angle measured from normal to the plane as shown in the figure).
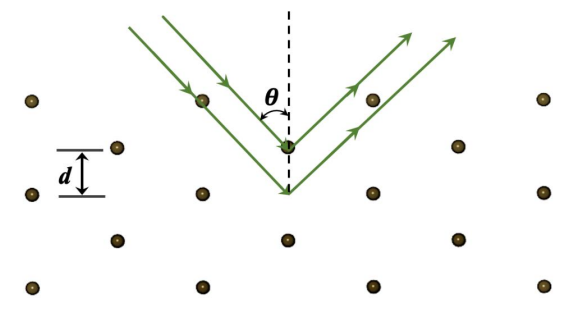
What is the value of \( a \)?
(a) 5.06 Å
(b) 8.77 Å
(c) 3.58 Å
(d) 5.46 Å
Check Answer
Option a
Q.No:7 TIFR-2025
A triangular lattice with lattice constant \(a\) has primitive vectors
\(\vec a_1\) and \(\vec a_2\), as shown in the figure.
The primitive wavevectors for the reciprocal lattice are given by:

a) \(\vec b_1 = \frac{2\pi}{a}\,\hat{x} + \frac{2\pi}{a\sqrt{3}}\,\hat{y},
\qquad
\vec b_2 = \frac{4\pi}{a\sqrt{3}}\,\hat{y}\)
b) \(\vec b_1 = \frac{2\pi}{a\sqrt{3}}\,\hat{x} + \frac{2\pi}{a}\,\hat{y},
\qquad
\vec b_2 = \frac{4\pi}{a\sqrt{3}}\,\hat{y}\)
c) \(\vec b_1 = \frac{2\pi}{a}\,\hat{x} - \frac{2\pi}{a\sqrt{3}}\,\hat{y},
\qquad
\vec b_2 = \frac{4\pi}{a\sqrt{3}}\,\hat{x}\)
d) \(\vec b_1 = \frac{2\pi}{a\sqrt{3}}\,\hat{x} - \frac{2\pi}{a}\,\hat{y},
\qquad
\vec b_2 = \frac{4\pi}{a\sqrt{3}}\,\hat{x}\)
