Q.No:1 JEST-2012
The wave function of a free particle in one dimension is given by \(\psi(x)=A\sin{x}+B\sin{3x}\). Then \(\phi(x)\) is an eigenstate of
(a) the position operator
(b) the Hamiltonian
(c) the momentum operator
(d) the parity operator
Check Answer
Option d
Q.No:2 JEST-2014
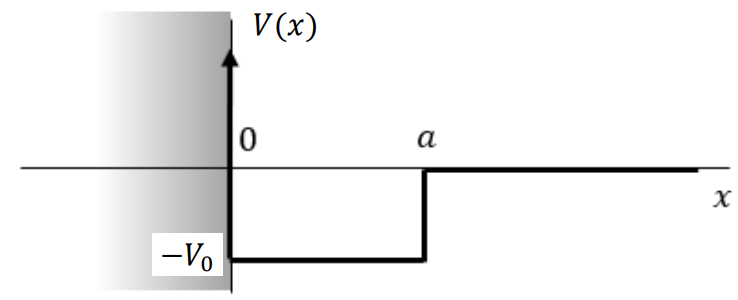
Consider a square well of depth \(-V_0\) and width \(a\) with \(V_0 a\) fixed. Let \(V_0\to \infty\) and \(a\to 0\). This potential well has
(a) No bound states
(b) \(1\) bound state
(c) t\(2\) bound states
(d) Infinitely many bound states
Check Answer
Option b
Q.No:3 JEST-2020
A free particle of energy \(E\), characterized by a plane wave of wavelength \(\lambda\) enters a region of constant potential \(-V\) (where \(E>V>0\)). Within the region of the potential, the wavelength of the particle is \(\lambda/2\). The ratio \(V/E\) is:
(a) \(-1/3\)
(b) \(-3\)
(c) \(3\)
(d) \(1/3\)
Check Answer
Option c
Q.No:4 JEST-2021
A quantum particle is moving in one dimension between rigid walls at \(x=-L\) and \(x=L\), under the influence of a potential (see figure). The potential has the uniform value \(V_0\) between \(-a<x<a\), and is \(0\) otherwise. Which one of the following graphs qualitatively represent the ground state wavefunction of this system? (You can assume that \(a\ll L\) and \(V_0\gg \pi^2/8mL^2\)).




Check Answer
Option d
Q.No:5 JEST-2022
A particle is confined in an infinite potential well of the form given below.
\[
V(x)=
\left\{
\begin{array}{ll}
4V_0 x(1-x), & \forall 0\leq x\leq 1 \\
\infty, & \text{otherwise}
\end{array}
\right.
\]
If the particle has energy \(E\geq V_0\), which of the following could be the form of its wavefunction?
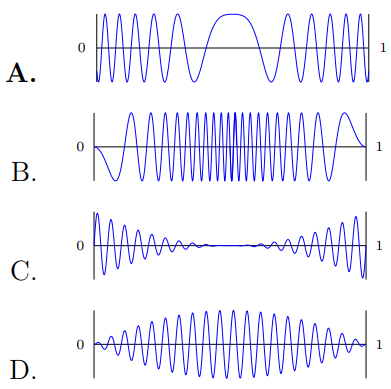
Check Answer
Option A
Q.No: 7 JEST-2023
Consider a quantum particle incident from the left on a step potential given by \(V_0 \theta (x)\), with energy \(E(> V_0)\); here \(\theta(x)\) is the unit step function. The scattering state of the particle is given
by
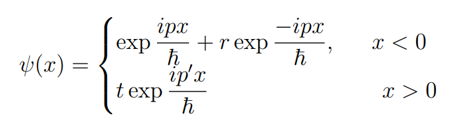
where \(p\) and \(p'\) are the momenta of the particle corresponding to the energy \(E\). Which of the following is true?
1) \(|r|^2 +\frac{p'}{p} |t|^2=1\)
2) \(|r|^2 + |t|^2=1\)
3) \(|r|^2 +\frac{p}{p'} |t|^2=1\)
4) \(r+t=1\)
Check Answer
Option 1
Q.No: 8 JEST-2023
Consider a free particle in one dimension described by the wavefunction:
\[\psi(x,t=0)= A \hspace{2mm} \text{exp} \hspace{2mm} \frac{ipx}{\hbar}+B \hspace{2mm} \text{exp} \hspace{2mm} \frac{-ipx}{\hbar}\]
The probability current density corresponding to \(\psi(x,t)\) at a later time \(t\) is:
1) \(\frac{p(|A|^2-|B|^2)}{m} \hspace{0.5mm} cos \hspace{0.5mm} ( \frac{p^2}{2 m \hbar} t)\)
2) \(\frac{p(|A|^2-|B|^2)}{m}\)
3) \(\frac{p(|A|^2+|B|^2)}{m}\)
4) \(\frac{p(|A|^2+|B|^2)}{m} \hspace{0.5mm} cos \hspace{0.5mm} ( \frac{p^2}{2 m \hbar} t)\)
Check Answer
Option 2
Q.No : 9 JEST-2024
A particle with energy \( E > 0 \) is incident from the right (\( x > 0 \)) on a one-dimensional potential composed of a delta-function barrier at \( x = 0 \) and a hard wall at \( x = -a \):
\[ V(x) = \begin{cases}
\alpha \delta(x), & x > -a \\
\infty, & x \leq -a
\end{cases} \]
where \( \alpha > 0 \) and \( a > 0 \). Let us define \( k^2 = \frac{2mE}{\hbar^2} \) and the dimensionless quantities: \( \xi = \kappa a \) and \( \beta = \frac{\hbar^2}{2m\alpha a} \). For some energy \( E \) the particle reflects from the barrier without any phase shift. Which of the following transcendental equations determines this energy?
Note that in the presence of the delta function barrier, the derivative of the wave function has a discontinuity at \[x = 0: \psi'(0^+) - \psi'(0^-) = \frac{\psi(0)}{\beta a}. \]
1) \( \tan \xi = -\beta \xi \)
2) \( \tan \xi = \beta \xi \)
3) \( \tanh \xi = \beta \xi \)
4) \( \tanh \xi = -\beta \xi \)
Check Answer
Option 1
Q.No : 10 JEST-2025
Suppose the wave function of a free particle in one dimension obeys
\[
\frac{d^{2}\psi}{dx^{2}} = -4\psi
\]
in units where \(\hbar = 1\). What is the magnitude of the momentum of the particle?
Check Answer
2
Q.No: 1 TIFR-2012
A particle in a one-dimensional potential has the wavefunction
\[
\psi(x)=\frac{1}{\sqrt{a}}\exp{\left(\frac{-|x|}{a}\right)}
\]
where \(a\) is a constant. It follows that for a positive constant \(V_0\), the potential \(V(x)=\)
(a) \(V_0 x^2\)
(b) \(V_0 |x|\)
(c) \(-V_0 \delta(x)\)
(d) \(-V_0/|x|\)
Check Answer
Option c
Q.No: 2 TIFR-2014
A particle is confined to a one-dimensional box of length \(L\). If a vanishingly thin but strongly repulsive partition is introduced in the exact centre of the box, and the particle is allowed to come to its ground state, then the probability density for finding the particle will appear as

Check Answer
Option a
Q.No: 3 TIFR-2015
It is required to construct the quantum theory of a particle of mass \(m\) moving in one dimension \(x\) under the influence of a constant force \(F\). The characteristic length-scale in this problem is
(a) \(\frac{\hbar}{mF}\)
(b) \(\left(\frac{\hbar^2}{mF}\right)\)
(c) \(\left(\frac{\hbar}{m^2 F}\right)\)
(d) \(\frac{mF}{\hbar^2}\)
Check Answer
Option b
Q.No:4 TIFR-2016
A particle is confined inside a one-dimensional potential well \(V(x)\), as shown on the right.

One of the possible probability distributions \(|\psi(x)|^2\) for an energy eigenstate for this particle is

Check Answer
Option a
Q.No: 5 TIFR-2017
Consider the \(1\)-D asymmetric double-well potential \(V(x)\) as sketched below.

The probability distribution \(p(x)\) of a particle in the ground state of this potential is best represented by

Check Answer
Option c
Q.No :6 TIFR-2019
A particle of mass \(m\), moving in one dimension, satisfies the modified Schr{\" o}dinger Equation
\[
-\frac{\hbar^2}{2m}\frac{d^2 \psi}{dx^2}+i\hbar u\frac{d\psi}{dx}=i\hbar \frac{d\psi}{dt}
\]
where \(u\) is the velocity of the substrate. If, now, this particle is treated as a Gaussian wave packet peaked at wavenumber \(k\), its group velocity will be \(\nu_g=\)
(a) \(\frac{\hbar k}{2m}-u\)
(b) \(\frac{\hbar k}{m}+u\)
(c) \(\frac{\hbar k}{m}-u\)
(d) \(-\frac{\hbar k}{2m}+u\)
Check Answer
Option c
Q.No:7 TIFR-2020
In a one-dimensional system, the boundary condition that the derivative of the wavefunction \(\psi'(x)\) should be continuous at every point is applicable whenever
(a) the wavefunction \(\psi(x)\) is itself continuous everywhere.
(b) there is a bound state and the potential is piecewise continuous.
(c) there is a bound state and the potential has no singularity anywhere.
(d) there are bound or scattering states with definite momentum.
Check Answer
Option c
Q.No:8 TIFR-2020
A particle moving in one dimension, is placed in an asymmetric square well potential \(V(x)\) as sketched below.


Check Answer
Option a
Q.No:9 TIFR-2022
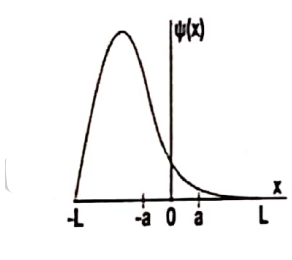
A particle moves in one dimension \(x\) under the influence of a potential \(V(x)\) as sketched in the figure below. The shaded region corresponds to infinite \(V\), i.e., the particle is not allowed to penetrate there.
If there is an energy eigenvalue \(E=0\), then \(a\) and \(V_0\) are related by
(a) \(a^2 V_0=\frac{n+(\frac{1}{2})^2 \pi^2}{2m}\)
(b) \(a^2 V_0=\frac{n^2 \pi^2}{2m}\)
(c) \(a^2 V_0=\frac{n+(\frac{1}{2}) \pi^2}{2m}\)
(d) \(a^2 V_0=\frac{n \pi^2}{2m}\)
Check Answer
Option a
Q.No:10 TIFR-2023
The value of the first derivative of the function
\[f(x)=\frac{2}{\sqrt{3}}e^{-\sqrt{3}x^2 |x|}\]
at \(x=0\) is \(f'(0)=\)
(a) Undefined
(b) \(0\)
(c) \(2\)
(d) \(2/\sqrt{3}\)

Q.No.1 Discussion :
Q.No.2 Discussion :
Q.No.3 Discussion :
Answer
Q.No.4 Discussion :
option D
Q.No.5 Discussion :
Q.No.6 Discussion :
Option C
Q.No.7 Discussion :
Q7 TIFR
Q.No.8 Discussion :
TIFR Q8
Q.No.9 Discussion :
Q.No.10 Discussion :
Q.No.11 Discussion :
Q.No.12 Discussion :
Reference Griffith
Q.No.13 Discussion :
Option a
Q.No.14 Discussion :
Refer Zettili Problem 4.13 Pg no. 270
Q.No.15 Discussion :
Option B
Q.No.16 Discussion :