Q.No:1 TIFR-2013
A plane electromagnetic wave travelling in a vacuum is characterised by the electric and magnetic fields
\[
\begin{array}{l}
\vec{E}=\hat{i}(30\pi Vm^{-1}\exp{i(\omega t+kz)} \\
\vec{H}=\hat{j}(H_0 Am^{-1}\exp{i(\omega t+kz)}
\end{array}
\]
If \(\omega, k>0\), the value of \(H_0\) must be
(a)
\(2\pi\)
(b)
\(0.67\)
(c)
\(0.25\)
(d)
\(0.94\)
Check Answer
Option c
Q.No:2 TIFR-2013
The magnetic vector potential \(\vec{A}(\vec{r})\) corresponding to a uniform magnetic field \(\vec{B}\) is taken in the form
\[
\vec{A}=\frac{1}{2}\vec{B}\times \vec{r}
\]
where \(\vec{r}\) is the position vector. If the electric field has the time-dependent form \(\vec{E}=\vec{E}_0(\vec{r})e^{i\omega t}\), where \(\omega\) is a constant, the gauge choice corresponding to this potential is a
(a)
Lorenz gauge
(b)
non-linear gauge
(c)
Coulomb gauge
(d)
time-varying gauge
Check Answer
Option c
Q.No:3 TIFR-2014
The instantaneous electric and magnetic fields created at a distance \(r\) by a point source at the origin are given by
\[
\vec{E}=\frac{A\cos{\omega t}}{2\pi \varepsilon_0 r}\hat{\theta} ~ \vec{H}=\frac{B\cos{\omega t}}{\mu_0 r}\hat{\varphi}
\]
where \(\omega, A, B\) are constants, and the unit vectors \((\hat{r}, \hat{\theta}, \hat{\varphi})\) form an orthonormal set. The time-averaged power radiated by the source is
(a)
\(\frac{\omega \varepsilon_0}{\mu_0}AB\)
(b)
\(\frac{c^3}{2\pi}AB\)
(c)
\(c^2 AB\)
(d)
\(\frac{2\pi\omega}{c}AB\)
Check Answer
Option c
Q.No:4 TIFR-2015
A light beam of intensity \(I_0\) passes at normal incidence through a flat plate of plastic kept in air. If reflection at the interface reduces the intensity by \(20\%\) and absorption on passing through the plate reduces the intensity by \(2\%\), the intensity of the emergent beam will be about
(a)
\(0.60 I_0\)
(b)
\(0.63 I_0\)
(c)
\(0.65 I_0\)
(d)
\(0.78 I_0\)
Check Answer
Option c
Q.No:5 TIFR-2015
A light source has a small filament at the centre of a spherical glass bulb of radius \(5 cm\) and negligible thickness. If this source emits \(100\) Watts of power in the form of spherical electromagnetic waves, the r.m.s. electric field \(E\) at the surface of the bulb (in units of Volt/m) will be approximately
(a)
\(1547\)
(b)
\(1094\)
(c)
\(109.4\)
(d)
\(15.47\)
Check Answer
Option b
Q.No:6 TIFR-2015
Measurement of the magnitudes of the electric field (\(E\)) and the magnetic field (\(B\)) in a plane-polarised electromagnetic wave in vacuum leads to the following results
\[
\frac{\partial E}{dy}=-\frac{\partial B}{\partial t} ~ \frac{\partial B}{dy}=-\frac{1}{c^2}\frac{\partial E}{\partial t}
\]
at all points where the measurement is made. In this case the electric vector \(\vec{E}\), the magnetic vector \(\vec{B}\) and the wave vector \(\vec{k}\) (with magnitude \(k\)) can be written in terms of the unit vectors \((\hat{x}, \hat{y}, \hat{z})\) along the Cartesian axes as
(a)
\(\vec{E}=E\hat{x}, \vec{B}=B\hat{y}, \vec{k}=k\hat{z}\)
(b)
\(\vec{E}=E\hat{x}, \vec{B}=B\hat{z}, \vec{k}=-k\hat{y}\)
(c)
\(\vec{E}=E\hat{x}, \vec{B}=-B\hat{z}, \vec{k}=k\hat{y}\)
(d)
\(\vec{E}=-E\hat{y}, \vec{B}=-B\hat{z}, \vec{k}=-k\hat{x}\)
Check Answer
Option c
Q.No:7 TIFR-2016
Consider the following system. Two circular loops of wire are placed horizontally, having a common axis passing vertically through the centre of each coil (see figure). The lower loop has radius \(r\) and carries a current \(i\) as shown in the figure. The upper loop has a radius \(R\) (\(R\gg r\)) and is at a distance \(x\) (\(x\gg R\)) above it.

If the lower loop is held fixed and the upper loop moves upwards with a uniform velocity \(\nu=dx/dt\), then the induced e.m.f. and the direction of the induced current in this loop will be
(a)
\(3i\mu_0 \pi^2 r^2 R^2 \nu/2x^4\); anti-clockwise
(b)
\(2i\mu_0 \pi^2 r^2 R^2 \nu/2x^4\); clockwise
(c)
\(3i\mu_0 \pi^2 r^2 R^2 \nu/2x^3\); anti-clockwise
(d)
\(2i\mu_0 \pi^2 r^2 R^2 \nu/3x^3\); clockwise
Check Answer
Option c
Q.No:8 TIFR-2017
A rectangular metallic loop with sides \(L_1\) and \(L_2\) is placed in the vertical plane, making an angle \(\varphi\) with respect to the \(x\)-axis, as shown in the figure, and a spatially uniform magnetic field \(\vec{B}=B\hat{y}\) is applied. The loop is free to rotate about the \(\hat{z}\)-axis (shown in the figure with a double line). The magnetic field changes with time at a constant rate
\[
\frac{dB}{dt}=\kappa
\]
If the resistance of the loop is \(R\), the torque \(\tau\) required to prevent the loop from rotating will be

(a)
\(-\kappa B\frac{(L_1 L_2)^2}{2R}\sin{2\varphi}\hat{z}\)
(b)
\(\kappa B\frac{(L_1 L_2)^2}{R}\sin{\varphi}\cos{\varphi}\hat{z}\)
(c)
\(\kappa B\frac{(L_1 L_2)^2}{2R}\sin{\varphi}\hat{z}\)
(d)
\(-\kappa B\frac{(L_1 L_2)^2}{R}\sin{\varphi}\hat{z}\)
Check Answer
Option a
Q.No:9 TIFR-2017
An electromagnetic wave in free space is described by
\[
\vec{E}(x, y, z, t)=\hat{z}E_0 \cos{\frac{1}{2}}(kx-\sqrt{3}ky-2\omega t)
\]
The Poynting vector associated with this wave is along the direction
(a)
\(\hat{x}+\sqrt{3}\hat{y}\)
(b)
\(\sqrt{3}\hat{x}+\hat{y}\)
(c)
\(-\sqrt{3}\hat{x}+\hat{y}\)
(d)
\(\hat{x}+\sqrt{3}\hat{y}\)
Check Answer
Option d
Q.No:10 TIFR-2018
The characteristic impedance of a co-axial cable is independent of the
(a)
core diameter
(b)
outer diameter
(c)
length of the cable
(d)
dielectric medium between the core and the outer mesh
Check Answer
Option c
Q.No:11 TIFR-2018
Consider a dipole antenna with length \(\ell\), charge \(q\) and frequency \(\omega\). The power emitted by the antenna at a large distance \(r\) is \(P\). Now suppose the length \(\ell\) is increased to \(\sqrt{2}\ell\), the charge is increased to \(\sqrt{3}q\) and the frequency is increased to \(\sqrt{5}\omega\). By what factor is the radiated power increased?
Check Answer
Ans 150
Q.No:12 TIFR-2018
A plane electromagnetic wave, which has an electric field
\[
\vec{E}(\vec{x}, t)=(P\hat{i}+Q\hat{j})\exp{i\omega\left(t-\frac{z}{c}\right)}
\]
is passing through vacuum. Here \(P, Q\) and \(\omega\) are all constants, while \(c\) is the speed of light in vacuo.
What is the average energy flux per unit time (in SI units) crossing a unit area placed normal to the direction of propagation of this wave, in terms of the above constants?
Check Answer
Ans
Q.No:13 TIFR-2019
A circular coil of conducting wire, of radius \(a\) and \(n\) turns, is placed in a uniform magnetic field \(\vec{B}\) along the axis of the coil and is then made to undergo simple harmonic oscillations along the direction of the axis. The current through the coil will be best described by

Check Answer
Option c
Q.No:13 TIFR-2019
A plane electromagnetic wave travelling through vacuum has electric field \(\vec{E}\) and magnetic field \(\vec{B}\) defined as
\[
\vec{E}=(\hat{i}+\hat{j})E_0\exp{i(\omega t-\vec{\kappa}\cdot \vec{x})}
\vec{B}=(\hat{i}-\hat{j}-\hat{k})E_0\exp{i(\omega t-\vec{\kappa}\cdot \vec{x})}
\]
where \(E_0\) and \(B_0\) are real constants. The time-averaged Poynting vector will be given by
(a)
\(\vec{S}=-\frac{2}{\sqrt{\epsilon_0 \mu_0}}E_0 B_0(\hat{i}-\hat{j}+2\hat{k})\)
(b)
\(\vec{S}=-\frac{1}{2}\sqrt{\frac{3\epsilon_0}{\mu_0}}E_0^2 (\hat{i}-\hat{j}+2\hat{k})\)
(c)
\(\vec{S}=\sqrt{\frac{\epsilon_0}{6\mu_0}}E_0^2 (-\hat{i}+\hat{j}-2\hat{k})\)
(d)
\(\vec{S}=\frac{1}{2}\sqrt{\frac{\epsilon_0}{\mu_0}}E_0^2 (\hat{i}-\hat{j}+2\hat{k})\)
Check Answer
Option c
Q.No:14 TIFR-2019
The magnetic vector potential corresponding to a uniform magnetic field \(\vec{B}\) is often taken as
\[
\vec{A}=\frac{1}{2}\vec{B}\times \vec{x}
\]
This choice is
(a)
valid in the Lorenz gauge.
(b)
valid in the Coulomb gauge.
(c)
valid in the Weyl gauge.
(d)
gauge invariant.
Check Answer
Option b
Q.No:15 TIFR-2020
A metallic wire of uniform cross-section and resistance \(R\) is bent into a circle of radius \(a\). The circular loop is placed in a magnetic field \(\vec{B}(t)\) which is perpendicular to the plane of the wire. This magnetic field is uniform over space, but its magnitude decreases with time at a constant rate \(k\), where
\[
k=-\frac{d|\vec{B}(t)|}{dt}
\]
The tension in the metallic wire is
(a)
\(\frac{\pi a^3 k}{2R}|\vec{B}(t)|\)
(b)
\(\frac{\pi a^3 k}{R}|\vec{B}(t)|\)
(c)
\(\frac{2\pi a^3 k}{R}|\vec{B}(t)|\)
(d)
zero
Check Answer
Option a
Q.No:16 TIFR-2020
The components of the electric and magnetic fields corresponding to a plane electromagnetic field propagating in vacuum satisfy
\[
E_x=E_y=-E_z=\frac{|\vec{E}|}{\sqrt{3}}
B_x=-B_y=\frac{|\vec{B}|}{\sqrt{2}}
B_z=0
\]
A unit vector along the direction of propagation of the plane wave is
(a)
\(\frac{\hat{i}+\hat{j}+2\hat{k}}{\sqrt{6}}\)
(b)
\(-\frac{\hat{i}+\hat{j}+2\hat{k}}{\sqrt{6}}\)
(c)
\(\frac{2\hat{i}-2\hat{j}+\hat{k}}{\sqrt{3}}\)
(d)
\(-\frac{2\hat{i}-2\hat{j}+\hat{k}}{\sqrt{3}}\)
Check Answer
Option b
Q.No:17 TIFR-2020
Consider the following situation.
An infinite plane metallic plate of thickness \(1.8 \hspace{1mm}\text{cm}\) is placed along the \(x\)-\(y\) plane, with the \(z\) axis normal to the sheet (see figure).

A plane radio wave of intensity \(I_0\) and frequency \(29.5 \hspace{1mm}\text{MHz}\) propagates in vacuum along the negative \(z\)-axis and strikes the metal foil at normal incidence.
If the metal of the foil has conductivity \(5.9 \hspace{1mm}\Omega^{-1}\text{m}^{-1}\) and magnetic permeability \(\mu\simeq 1\), the intensity \(I_E\) of the emergent wave will be approximately
(a)
\(0.26 I_0\)
(b)
\(0.51 I_0\)
(c)
\(0.29\times 10^{-7} I_0\)
(d)
\(2.08\times 10^{-4} I_0\)
Check Answer
Option a
Q.No:18 TIFR-2021
The Cartesian components of the electric field \(\vec{E}=\{E_i\mid i=1, 2, 3\}\) in a charge-free region of space are
\[
E_i=C_i+\sum_{j} r_j D_{ji}
\]
where \(C_i\) and \(D_{ji}\)'s are constant. The matrix of constants \(D_{ji}\) is
(a)
symmetric and traceless
(b)
symmetric but not traceless
(c)
anti-symmetric and traceless
(d)
anti-symmetric but not traceless
Check Answer
Option a
Q.No:19 TIFR-2021
An oscillating point dipole of moment \(\vec{p}(t)=\hat{z} p_0 \cos{\omega t}\) generates time-dependent electric and magnetic fields. At distances \(r\) far away from the dipole, the vector potential due to this dipole, in SI units, is
\[
\vec{A}=\hat{z} \frac{\mu_0 p_0 \omega}{4\pi r} \sin{\omega\left(t-\frac{r}{c}\right)}
\]
The total power radiated from this dipole is
(a)
\(\frac{\mu_0 p_0^2 \omega^4}{12\pi c}\)
(b)
\(\frac{\mu_0 p_0^2 \omega^4}{8\pi c}\)
(c)
\(\frac{\mu_0 p_0^2 \omega^4}{16\pi^2 c}\)
(d)
\(\frac{\mu_0 p_0^2 \omega^4}{24\pi c}\)
Check Answer
Option a
Q.No:20 TIFR-2022
If an electron is set into oscillatory motion by the electric field of a laser of intensity 150 W \(m^{-2}\) and wavelength 554 nm, the amplitudes of its displacement and velocity, respectively, are expected to be
(a)
\(5.1 \times 10^{-18} \hspace{0.3mm} m \\ 1.7 \times 10^{-2}m \hspace{0.3mm} s^{-1}\)
(b)
\(3.4 \times 10^{-17} \hspace{0.3mm} m \\ 1.0 \times 10^{-1}m \hspace{0.3mm} s^{-1}\)
(c)
\(3.4 \times 10^{-16} \hspace{0.3mm} m \\ 1.7 \times 10^{-1}m \hspace{0.3mm} s^{-1}\)
(d)
\(3.4 \times 10^{-18} \hspace{0.3mm} m \\ 1.7 \times 10^{-2}m \hspace{0.3mm} s^{-1}\)
Check Answer
Option a
Q.No:21 TIFR-2022
The power radiated by a point charge \(q\) moving rapidly with a uniform speed \(v\) in a circle of radius \(R\) will be
(a)
\(\frac{q^2 c }{6 \pi \epsilon_0 R^2} (\frac{v^2}{c^2-v^2})^2\)
(b)
\(\frac{q^4 c^2 }{6 \pi \epsilon_0 R^2} (\frac{v^2}{c^2-v^2})^2\)
(c)
\(\frac{q^3 c }{6 \pi \epsilon_0 R^4} \frac{v^2}{c^2-v^2}\)
(d)
\(\frac{q^2 c^3 }{6 \pi \epsilon_0 R^3} \frac{v^2}{c^2-v^2}\)
Check Answer
Option a
Q.No:22 TIFR-2023
A beam of unpolarized microwave radiation is incident along the x-axis on a grid of metal wires in the yz-plane with wires running along the y-axis (see figure below).
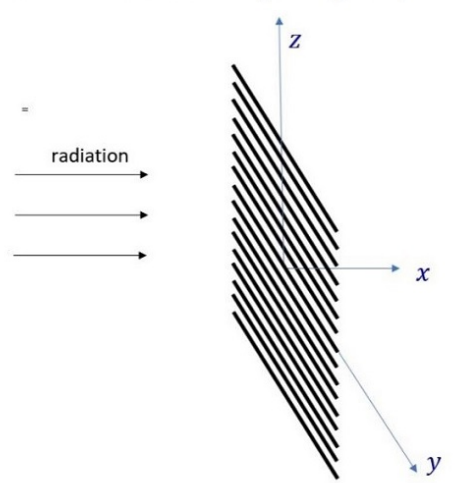
If the width of each wire and the spacing between the adjacent wires is less than the wavelength of the microwave, the observation would be that
(a)
The transmitted wave would be polarized along the z-axis
(b)
The transmitted wave would be polarized along the y-axis
(c)
The transmitted wave would be unpolarized
(d)
no wave will pass through as the spacing is smaller than the wavelength
Check Answer
Option a
Q.No:23 TIFR-2023
Consider the following situation. A uniform magnetic field \(\vec{B}\) pointing into the plane of the paper is present everywhere inside the rectangular region shown shaded in the adjoining figure. Outside the rectangular region, there is no magnetic field.
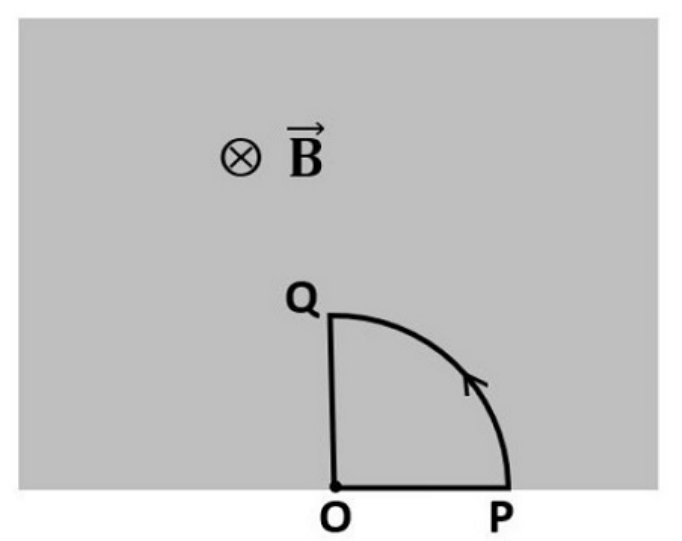
A closed loop of conducting wire is placed inside the rectangular region as shown in the figure at \(t=0\). The loop is then rotated counterclockwise with a uniform angular velocity \(\omega\) about an axis perpendicular to the paper passing through the point \(O\).
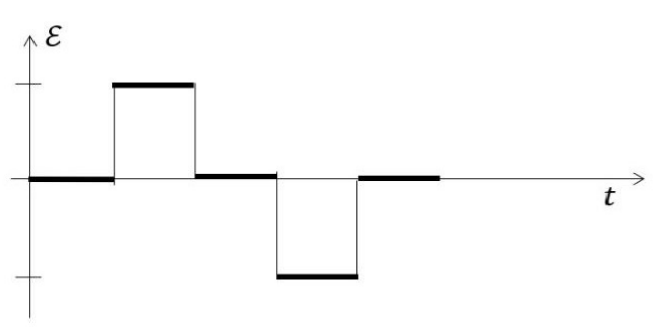
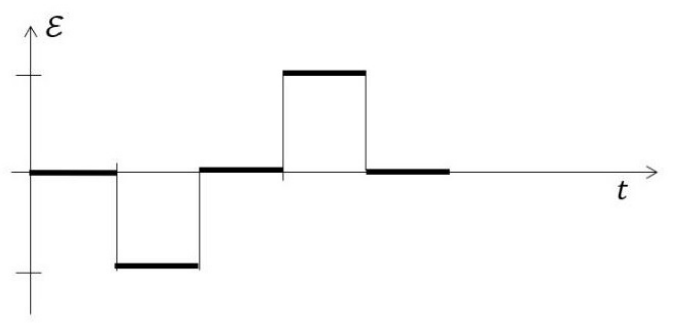
If the direction along PQOP is taken to be positive, then a correct graph for the EMF \(\epsilon\) generated in the loop is
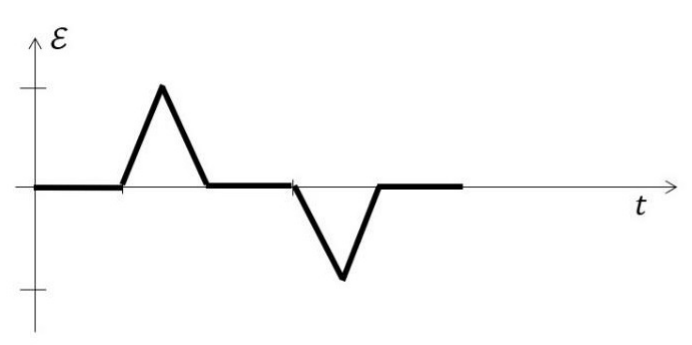
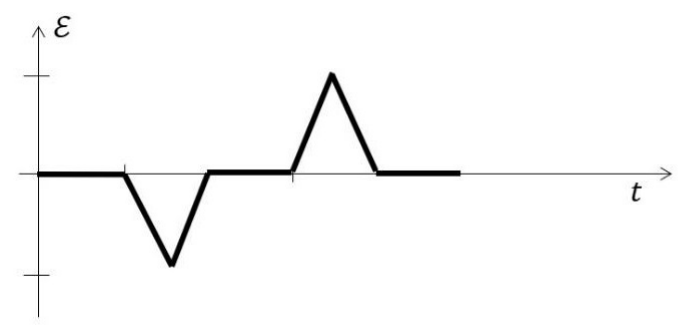
Check Answer
Option b
Q.No:24 TIFR-2023
A small satellite S has a rectangular solar sail of dimensions 8 m \(\times\) 4 m, which propels the satellite upon receiving sunlight. One half of the sail is a perfect reflector, while the other half is a perfect absorber, as shown in the figure.

Assuming uniform sunlight incident normally on the sail with an intensity
1370 W \(m^{-2}\) and ignoring the satellite’s shadowing effects, the instantaneous torque experienced by the satellite is
(a)
\(1.46 \times 10^{-4}\) N-m
(b)
\(2.92 \times 10^{-4}\) N-m
(c)
\(0.73 \times 10^{-4}\) N-m
(d)
\(2.19 \times 10^{-4}\) N-m
Check Answer
Option a
Q.No:26 TIFR-2023
A charge \(e\) is moving with an angular frequency \(\omega\) along a circle of radius \(a\) always keeping a small distance \(d\) (\(d\ll a\)) from a grounded infinite conducting plane.
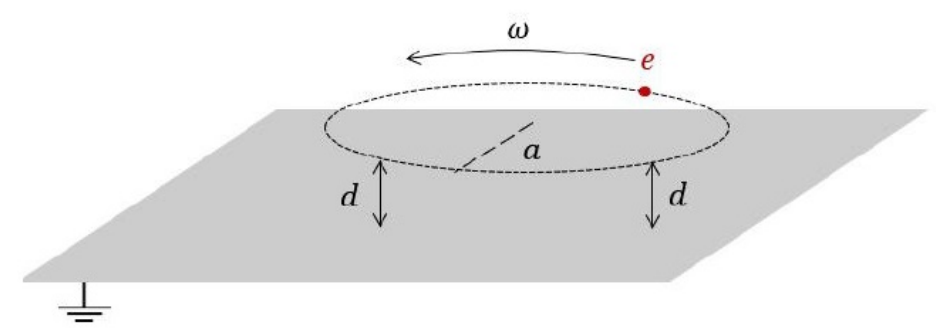
The leading dependence of the radiated power \(P(\omega)\) at a distance \(r\) (\(r \gg a\)) will be
(a)
\(P(\omega) \propto \omega^4\)
(b)
\(P(\omega) \propto \omega^2\)
(c)
\(P(\omega) \propto \omega^6\)
(d)
\(P(\omega) \propto \omega^3\)
Check Answer
Option a
Q.No:27 TIFR-2023
For an electromagnetic wave propagating through a rectangular waveguide, the electric and magnetic fields
(a)
are always perpendicular to each other
(b)
are never perpendicular to each other
(c)
are perpendicular to each other only in TE mode
(d)
are perpendicular to each other only in TM mode
Check Answer
Option b
Q.No:28 TIFR-2024
A conducting square loop of wire (side \( a \)) lies on a table, at a distance \( s \) from an infinite straight wire as shown in the figure. The infinite wire carries a current \( I \) in the \( x \) direction as shown. If one now pulls the loop directly away from the wire in the \( y \) direction at a constant speed \( v \), what is the generated EMF in the loop? In what direction (clockwise or counterclockwise) does the current flow in the loop?

(a) \( \frac{a^2v\mu_0I}{2\pi(as+s^2)} \), anticlockwise
(b) \( \frac{a^2v\mu_0I}{2\pi(as+s^2)} \), clockwise
(c) \( \frac{av\mu_0I}{2\pi(a+s)} \), anticlockwise
(d) \( \frac{av\mu_0I}{2\pi(a+s)} \), clockwise
Check Answer
Option a
Q.No:29 TIFR-2024
Consider a charge particle detection chamber as shown in the figure below. The chamber is made of a set of parallel plates separated by 20 mm distance and connected to the external resistance \(\left( R = 100 \, \Omega \right)\) as shown in the figure along with the high voltage power supply of 1 kV.
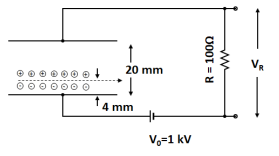
The chamber is filled with Argon (Ar) gas (ionization energy 16 eV). If a charged particle passes through the chamber and loses sufficient energy, it ionizes the Ar atoms and generates a small voltage pulse across the resistance \( R \).
In an experiment, an alpha particle of energy 5.5 MeV enters the chamber at a distance of 4 mm from the bottom plate, as shown, generating ion-electron pairs. If the effective capacitance of the chamber is 100 pF, the measured voltage pulse shape would be best described as:
(a) A sharp voltage pulse followed by a very weak broad pulse
(b) Two sharp voltage pulses of equal magnitude and opposite signs
(c) Two sharp voltage pulses of the same magnitude and sign
(d) No voltage pulse would be generated as both electrons and ions will neutralise the charge collected by the capacitor
Check Answer
Option a
Q.No:30 TIFR-2024
A smartphone emits electromagnetic radiation with a power of 1 Watt. What is the approximate value of the r.m.s. magnetic field at a distance 25 cm from the phone?
(a) \( 10^{-7} \) Tesla
(b) \( 10^{-5} \) Tesla
(c) \( 10^{-9} \) Tesla
(d) \( 10^{-11} \) Tesla
Check Answer
Option a
Q.No:31 TIFR-2024
Incident unpolarized light is reflected from a glass (\( n_g = 1.65 \)) plate immersed in ethyl alcohol (\( n_a = 1.36 \)) and this reflection is found to be completely linearly polarised. Find the angle at which the incident light would be transmitted through the plate.
(a) \( 39.5^\circ \)
(b) \( 31.6^\circ \)
(c) \( 50.5^\circ \)
(d) \( 69.3^\circ \)
Check Answer
Option a
Q.No:32 TIFR-2025
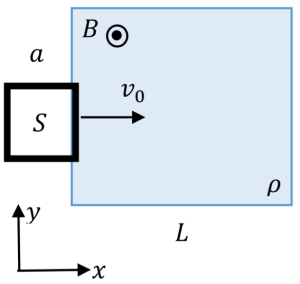
A small metallic wire with mass \(m\) and electric resistance \(R\) is bent into a closed
square shape \(S\) with sides \(a\). It passes through a region \(\rho\) of length
\(L>a\) with magnetic field \(B\hat{z}\). The initial velocity \(v_{0}\hat{x}\) of the
square is large enough that it emerges out of \(\rho\) from the right. What is the
final velocity of \(S\) after it completely emerges from \(\rho\)?
a) \(v_{0}\left(1-\frac{a^{3}B^{2}}{mRv_{0}}\right)^{2}\hat{x}\)
b) \(v_{0}\exp\!\left(-\,\frac{a^{2}B^{2}L}{mRv_{0}}\right)\hat{x}\)
c) \(v_{0}\left(1-\frac{a^{3}B^{2}}{mRv_{0}}\right)\hat{x}\)
d) \(v_{0}\hat{x}\)
Check Answer
Option a
Q.No:33 TIFR-2025
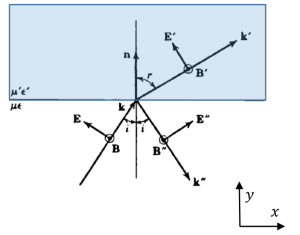
Light in a medium with electric permittivity \(\varepsilon\) and magnetic
permeability \(\mu\) is incident on a medium with electric permittivity
\(\varepsilon'\) and magnetic permeability \(\mu'\). The angle of incidence is
\(i\). The \(\vec{E}\) field is linearly polarized in the plane as shown, and the
\(\vec{B}\) field is in the \(\hat{z}\) direction. Which of the following is a
correct boundary condition on the fields?
a) \(\varepsilon\bigl(E\sin i + E''\sin i\bigr) = \varepsilon' E' \sin r\)
b) \(\varepsilon\bigl(E\cos i - E''\cos i\bigr) = \varepsilon' E' \cos r\)
c) \(E\sin i + E''\sin i = E' \sin r\)
d) \(\mu\bigl(B + B''\bigr) = \mu' B'\)
Check Answer
Option a
Q.No:34 TIFR-2025
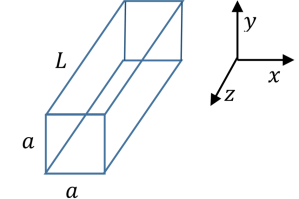
A very long square pipe with length \(L\) and cross–sectional area \(a^{2}\) \((L\gg a)\) has
ideal conducting walls. A travelling mode with
\[
E_{z}(\vec{r},t)=A \sin\frac{\pi x}{a}\,\sin\frac{\pi y}{a}\,e^{ikz-i\omega t}
\]
is excited in the pipe. What is the relation between \(k\) and \(\omega\)?
(Assume \(\varepsilon \approx \varepsilon_{0},\ \mu \approx \mu_{0}\).)
a) \(k=\sqrt{\frac{\omega^{2}}{c^{2}}-\frac{2\pi^{2}}{a^{2}}}\)
b) \(k=\sqrt{\frac{\omega^{2}}{c^{2}}+\frac{2\pi^{2}}{a^{2}}}\)
c) \(k=\frac{\omega}{c}\)
d) \(k=\sqrt{\frac{\omega^{2}}{c^{2}}+\frac{\pi^{2}}{a^{2}}}\)
Check Answer
Option a
Q.No:35 TIFR-2025
Consider two relativistic particles, each with mass \(m\) and momentum of magnitude
\(p\), colliding head–on. As a result of the collision, two heavier particles are
produced, each with mass \(\alpha m\), where \(\alpha > 1\). The minimum value of
\(p\) required for this collision to occur is:
a) \(\sqrt{\alpha^{2}-1}\,m c\)
b) \((\alpha-1)\,m c\)
c) \(2\alpha m c\)
d) \((\sqrt{\alpha}-1)^{2} m c\)
Check Answer
Option a
Q.No:36 TIFR-2025
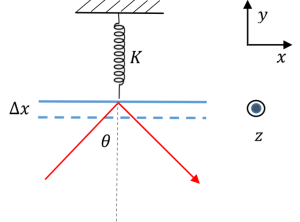
A perfect mirror is hanging from the ceiling via a spring of spring constant \(K\).
A plane–wave laser beam with area \(A\) and
\[
\vec{E}(\vec{r},t)=E_{0}\hat{z}\cos(\vec{k}\cdot\vec{r}-\omega t)
\]
is incident on the mirror at an angle \(\theta\), and lifts the mirror by \(\Delta x\).
What is \(\Delta x\) (averaged over a cycle) in terms of \(K, E_{0}, \epsilon_{0}\) and \(\mu_{0}\)?
a)\(\displaystyle \Delta x = \frac{E_{0}^{2}A\cos\theta}{Kc}
\sqrt{\frac{\epsilon_{0}}{\mu_{0}}}\)
b) \(\displaystyle \Delta x = \frac{E_{0}^{2}A\cos^{2}\theta}{Kc}
\sqrt{\frac{\epsilon_{0}}{\mu_{0}}}\)
c) \(\displaystyle \Delta x = \frac{\epsilon_{0}E_{0}^{2}A}{Kc}
\sqrt{\frac{\epsilon_{0}}{\mu_{0}}}\)
d)\(\displaystyle \Delta x = \frac{2\epsilon_{0}E_{0}^{2}A\cos^{2}\theta}{Kc}
\sqrt{\frac{\epsilon_{0}}{\mu_{0}}}\)
