Electrostatics CSIR - S. N. Bose Physics Learning Center

Q.No:1 CSIR Dec-2014

A solid sphere of radius \(R\) has a charge density, given by \[ \rho(r)=\rho_0\left(1-\frac{ar}{R}\right), \] where \(r\) is the radial coordinate and \(\rho_0, a\) and \(R\) are positive constants. If the magnitude of the electric field at \(r=R/2\) is \(1.25\) times that at \(r=R\), then the value of \(a\) is

(1) \(2\)

(2) \(1\)

(3) \(1/2\)

(4) \(1/4\)

Check Answer

Option 2

Q.No:2 CSIR Dec-2014

The electrostatic lines of force due to a system of four point charges is sketched below.

At a large distance \(r\), the leading asymptotic behaviour of the electrostatic potential is proportional to

(1) \(r\)

(2) \(r^{-1}\)

(3) \(r^{-2}\)

(4) \(r^{-3}\)

Check Answer

Option 4

Q.No:3 CSIR June-2015

Suppose the yz-plane forms a chargeless boundary between two media of permittivities \(\epsilon_{\text{left}}\) and \(\epsilon_{\text{right}}\) where \(\epsilon_{\text{left}}: \epsilon_{\text{right}} = 1:2\). If the uniform electric field on the left is \(\overrightarrow{E}_{\text{left}} = c(\hat{i} + \hat{s} + \hat{k})\) (where c is a constant), then the electric field on the right \(\overrightarrow{E}_{\text{right}}\) is

(1) \(c(\hat{2i}+\hat{j}+\hat{k})\)

(2) \(c(\hat{i}+\hat{2j}+\hat{2k})\)

(3) \(c(1/2\hat{i}+\hat{j}+\hat{k})\)

(4) \(c(\hat{i}+1/2\hat{j}+1/2\hat{k})\)

Check Answer

Option 3

Q.No:4 CSIR Dec-2015

A hollow metallic sphere of radius \(a\), which is kept at a potential \(V_0\), has a charge \(Q\) at its centre. The potential at a point outside the sphere, at a distance \(r\) from the centre, is

(1) \(V_0\)

(2) \(\frac{Q}{4\pi \epsilon_0 r}+\frac{V_0 a}{r}\)

(3) \(\frac{Q}{4\pi \epsilon_0 r}+\frac{V_0 a^2}{r^2}\)

(4) \(\frac{V_0 a}{r}\)

Check Answer

Option 4

Q.No:5 CSIR Dec-2015

Consider a charge \(Q\) at the origin of \(3\)-dimensional coordinate system. The flux of the electric field through the curved surface of a cone that has a height \(h\) and a circular base of radius \(R\) (as shown in the figure) is

(1) \(\frac{Q}{\epsilon_0}\)

(2) \(\frac{Q}{2\epsilon_0}\)

(3) \(\frac{hQ}{R\epsilon_0}\)

(4) \(\frac{QR}{2h\epsilon_0}\)

Check Answer

Option 2

Q.No:6 CSIR June-2016

Four equal charges of \(+Q\) each are kept at the vertices of a square of side \(R\). A particle of mass \(m\) and charge \(+Q\) is placed in the plane of the square at a short distance \(a\) (\(\ll R\)) from the centre. If the motion of the particle is confined to the plane, it will undergo small oscillations with an angular frequency

(1) \(\sqrt{\frac{Q^2}{2\pi \epsilon_0 R^3 m}}\)

(2) \(\sqrt{\frac{Q^2}{\pi \epsilon_0 R^3 m}}\)

(3) \(\sqrt{\frac{\sqrt{2} Q^2}{\pi \epsilon_0 R^3 m}}\)

(4) \(\sqrt{\frac{Q^2}{4\pi \epsilon_0 R^3 m}}\)

Check Answer

Option 3

Q.No:7 CSIR June-2016

Two parallel plate capacitors, separated by distances \(x\) and \(1.1x\) respectively, have a dielectric material of dielectric constant \(3.0\) inserted between the plates, and are connected to a battery of voltage \(V\). The difference in charge on the second capacitor compared to the first is

(1) \(+66\%\)

(2) \(+20\%\)

(3) \(-3.3\%\)

(4) \(-10\%\)

Check Answer

Option 4

Q.No:8 CSIR June-2016

The half space regions \(x>0\) and \(x<0\) are filled with dielectric media of dielectric constants \(\epsilon_1\) and \(\epsilon_2\) respectively. There is a uniform electric field in each part. In the right half, the electric field makes an angle \(\theta_1\) to the interface. The corresponding angle \(\theta_2\) in the left half satisfies

(1) \(\epsilon_1 \sin{\theta_2}=\epsilon_2 \sin{\theta_1}\)

(2) \(\epsilon_1 \tan{\theta_2}=\epsilon_2 \tan{\theta_1}\)

(3) \(\epsilon_1 \tan{\theta_1}=\epsilon_2 \tan{\theta_2}\)

(4) \(\epsilon_1 \sin{\theta_1}=\epsilon_2 \sin{\theta_2}\)

Check Answer

Option 3

Q.No:9 CSIR June-2016

Consider a sphere \(S_1\) of radius \(R\) which carries a uniform charge of density \(\rho\). A smaller sphere \(S_2\) of radius \(a< R/2\) is cut out and removed from it. The centres of the two spheres are separated by the vector \(\vec{b}=\hat{n} R/2\), as shown in the figure.

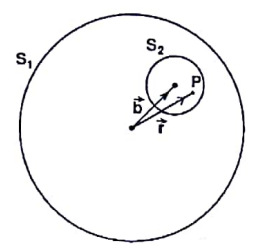
The electric field at a point \(P\) inside \(S_2\) is

(1) \(\frac{\rho R}{3\varepsilon_0} \hat{n}\)

(2) \(\frac{\rho R}{3\varepsilon_0 a} (\vec{r}-\hat{n}a)\)

(3) \(\frac{\rho R}{6\varepsilon_0} \hat{n}\)

(4) \(\frac{\rho a}{3\varepsilon_0 R} \vec{r}\)

Check Answer

Option 3

Q.No:10 CSIR June-2016

Two completely overlapping semi-circular parallel plates comprise a capacitive transducer. One of the plates is rotated by an angle of \(10^{\circ}\) relative to their common centre. Ignoring edge effects, the ratio, \(I_n:I_o\), of sensitivity of the transducer in the new configuration with respect to the original one, is

(1) \(8:9\)

(2) \(11:12\)

(3) \(17:18\)

(4) \(35:36\)

Check Answer

Option 3

Q.No:11 CSIR Dec-2016

The charge per unit length of a circular wire of radius \(a\) in the \(xy\)-plane, with its centre at the origin, is \(\lambda=\lambda_0\cos{\theta}\), where \(\lambda_0\) is a constant and the angle \(\theta\) is measured from the positive \(x\)-axis. The electric field at the centre of the circle is

(1) \(\vec{E}=-\frac{\lambda_0}{4\epsilon_0 a}\hat{i}\)

(2) \(\vec{E}=\frac{\lambda_0}{4\epsilon_0 a}\hat{i}\)

(3) \(\vec{E}=-\frac{\lambda_0}{4\epsilon_0 a}\hat{j}\)

(4) \(\vec{E}=\frac{\lambda_0}{4\pi\epsilon_0 a}\hat{k}\)

Check Answer

Option 1

Q.No:12 CSIR Dec-2016

Two uniformly charged insulating solid spheres A and B, both of radius \(a\), carry total charges \(+Q\) and \(-Q\), respectively. The spheres are placed touching each other as shown in the figure.

If the potential at the centre of the sphere A is \(V_A\) and that at the centre of B is \(V_B\), then the difference \(V_A-V_B\) is

(1) \(\frac{Q}{4\pi \varepsilon_0 a}\)

(2) \(\frac{-Q}{2\pi \varepsilon_0 a}\)

(3) \(\frac{Q}{2\pi \varepsilon_0 a}\)

(4) \(\frac{-Q}{4\pi \varepsilon_0 a}\)

Check Answer

Option 3

Q.No:13 CSIR June-2017

Two long hollow co-axial conducting cylinders of radii \(R_1\) and \(R_2\) (\(R_1< R_2\)) are placed in vacuum as shown in the figure below.

The inner cylinder carries a charge \(+\lambda\) per unit length and the outer cylinder carries a charge \(-\lambda\) per unit length. The electrostatic energy per unit length of this system is

(1) \(\frac{\lambda^2}{\pi \epsilon_0} \ln{(R_2/R_1)}\)

(2) \(\frac{\lambda^2}{4\pi \epsilon_0} \ln{(R_2^2/R_1^2)}\)

(3) \(\frac{\lambda^2}{4\pi \epsilon_0} \ln{(R_2/R_1)}\)

(4) \(\frac{\lambda^2}{2\pi \epsilon_0} \ln{(R_2/R_1)}\)

Check Answer

Option 3

Q.No:14 CSIR Dec-2017

Two point charges \(+3Q\) and \(-Q\) are placed at \((0, 0, d)\) and \((0, 0, 2d)\), respectively, above an infinite grounded conducting sheet kept in the \(xy\) plane. At a point \((0, 0, z)\), where \(z\gg d\), the electrostatic potential of this charge configuration would approximately be

(1) \(\frac{1}{4\pi \epsilon_0} \frac{d^2}{z^3} Q\)

(2) \(\frac{1}{4\pi \epsilon_0} \frac{2d}{z^2} Q\)

(3) \(\frac{1}{4\pi \epsilon_0} \frac{3d}{z^2} Q\)

(4) \(-\frac{1}{4\pi \epsilon_0} \frac{d^2}{z^3} Q\)

Check Answer

Option 2

Q.No:15 CSIR Dec-2017

A rectangular piece of dielectric material is inserted partially into the (air) gap between the plates of a parallel plate capacitor. The dielectric piece will

(1) remain stationary where it is placed

(2) be pushed out from the gap between the plates

(3) be drawn inside the gap between the plates and its velocity does not change sign

(4) execute an oscillatory motion in the region between the plates

Check Answer

Option 4

Q.No:16 CSIR June-2018

Two point charges \(+2Q\) and \(-Q\) are kept at points with Cartesian coordinates \((1, 0, 0)\) and \((2, 0, 0)\), respectively, in front of an infinite grounded conducting plate at \(x=0\). The potential at \((x, 0, 0)\) for \(x\gg 1\) depends on \(x\) as

(1) \(x^{-3}\)

(2) \(x^{-5}\)

(3) \(x^{-2}\)

(4) \(x^{-4}\)

Check Answer

Option 4

Q.No:17 CSIR Dec-2018

An electric dipole of dipole moment \(\vec{P}=qb\hat{i}\) is placed at the origin in the vicinity of two charges \(+q\) and \(-q\) at \((L,b)\) and \((L,-b)\), respectively, as shown in the figure below.

The electrostatic potential at the point \((L/2, 0)\) is

(1) \(\frac{qb}{\pi \epsilon_0} \left(\frac{1}{L^2}+\frac{2}{L^2+4b^2}\right)\)

(2) \(\frac{4qb}{\pi \epsilon_0[L^2+4b^2]^{3/2}}\)

(3) \(\frac{qb}{\pi \epsilon_0 L^2}\)

(4) \(\frac{3qb}{\pi \epsilon_0 L^2}\)

Check Answer

Option 3

Q.No:18 CSIR Dec-2019

The \(yz\)-plane at \(x=0\) carries a uniform surface charge density \(\sigma\). A unit point charge is moved from a point \((\delta, 0, 0)\) on one side of the plane to a point \((-\delta, 0, 0)\) on the other side. If \(\delta\) is an infinitesimally small positive number, the work done in moving the charge is

(1) \(0\)

(2) \(\frac{\sigma}{\epsilon_0}\delta\)

(3) \(-\frac{\sigma}{\epsilon_0}\delta\)

(4) \(\frac{2\sigma}{\epsilon_0}\delta\)

Check Answer

Option 1

Q.No:19 CSIR Dec-2019

A parallel plate capacitor, with \(1 cm\) separation between the plates, has two layers of dielectric with dielectric constants \(\kappa=2\) and \(\kappa=4\), as shown in the figure below. If a potential difference of \(10 V\) is applied between the plates, the magnitude of the bound surface charge density (in units of \({C/m^2}\)) at the junction of the dielectrics is

(1) \(250\epsilon_0\)

(2) \(2000\epsilon_0/3\)

(3) \(2000\epsilon_0\)

(4) \(200\epsilon_0/3\)

Check Answer

Option 2

Q.No:20 Assam CSIR Dec-2019

A non-conducting thin ellipsoidal shell defined by the equation \(x^2+2y^2+3z^2=a^2\) has a net charge \(Q\) spread uniformly over its surface. The flux passing through a hemispherical surface defined by \(x^2+y^2+z^2=a^2\) and \(z>0\), is

(1) \(Q/(\sqrt{3}\epsilon_0)\)

(2) \(Q/\epsilon_0\)

(3) \(Q/(2\epsilon_0)\)

(4) \(Q/(3\epsilon_0)\)

Check Answer

Option 3

Q.No:21 CSIR June-2020

Three point charges \(q\) are placed at the corners of an equilateral triangle. Another point charge \(-Q\) is placed at the centroid of the triangle. If the force on each of the charges \(q\) vanishes, then the ratio \(Q/q\) is

(a) \(\sqrt{3}\)

(b) \(\frac{1}{\sqrt{3}}\)

(d) \(\frac{1}{3}\)

Check Answer

Option b

Q.No:22 CSIR Feb-2022

A linear diatomic molecule consists of two identical small electric dipoles with an equilibrium separation \(R\) , which is assumed to be a constant. Each dipole has charges \(\pm q\) of mass \(m\) separated by \(r\) when the molecule is at equilibrium. Each dipole can execute simple harmonic motion of angular frequency \(\omega\)

Recall that the interaction potential between two dipoles of moments \(\vec{p_1}\) and \(\vec{p_2}\), separated by \(R_{12}=R_{12}\hat{n}\) is \[(\vec{p_1}.\vec{p_2}-3(\vec{p_1}.\hat{n})(\vec{p_2.\hat{n}}))/(4\pi\epsilon_0R_{12}^3)\]. Assume that \(R\gg r\) and let \(\Omega^2=\frac{q^2}{4\pi\epsilon_0mR^3}\) . The angular frequencies of small oscillations of the diatomic molecule are

(1) \(\frac{1}{3}\)

(2) \(\frac{1}{3}\)

(3) \(\frac{1}{3}\)

(4) \(\frac{1}{3}\)

Check Answer

Option 3

Q.No:23 CSIR Sep-2022

Two positive and two negative charges of magnitude \(q\) are placed on the alternate vertices of a cube of side \(a\) (as shown in the figure)

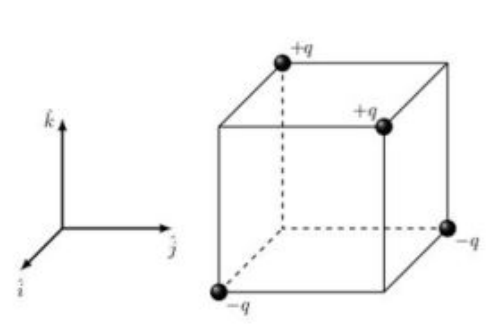
The electric dipole moment of this charge configeration is

(1) \(-2qa \hspace{1mm}\hat{k}\)

(2) \(2qa \hspace{1mm}\hat{k}\)

(3) \(2qa \hspace{1mm}(\hat{i}+\hat{j})\)

(4) \(2qa \hspace{1mm}(\hat{i}-\hat{j})\)

Check Answer

Option 2

Q.No:24 CSIR June-2023

The electric potential on the boundary of a spherical cavity of radius \(R\), as a function of the polar angle \(\theta\), is \(V_0\cos^2\frac{\theta}{2}\). The charge density inside the cavity is zero everywhere. The potential at a distance \(R/2\) from the centre of the sphere is

1) \(\frac{1}{2}V_0(1+\frac{1}{2}\cos\theta)\)

2) \(\frac{1}{2}V_0\cos\theta\)

3) \(\frac{1}{2}V_0(1+\frac{1}{2}\sin\theta)\)

4) \(\frac{1}{2}V_0\sin\theta\)

Check Answer

Option 1

Q.No:25 CSIR Dec-2023

A conducting shell of radius \( R \) is placed with its centre at the origin as shown below. A point charge \( Q \) is placed inside the shell at a distance \( a \) along the x-axis from the centre.

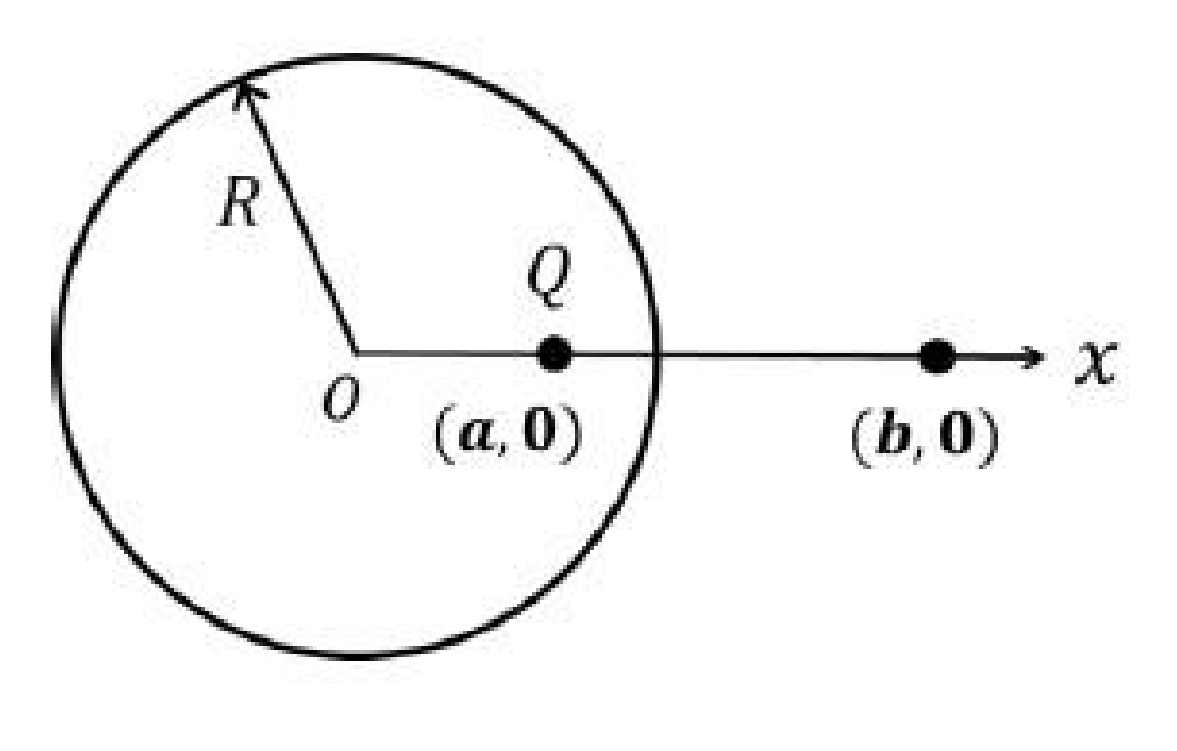
The electric field at a distance \( b > R \) along the x-axis from the centre is

1) \( \frac{Q}{4\pi\epsilon_0 b^2} \hat{X} \)

2) \( \frac{Q}{4\pi\epsilon_0} \left[ \frac{1}{(b-a)^2} - \frac{aR}{(ab-R^2)^2} \right] \hat{X} \)

3) \( \frac{Q}{4\pi\epsilon_0} \left[ \frac{1}{(b-a)^2} + \frac{aR}{(ab-R^2)^2} \right] \hat{X} \)

4) \( \frac{Q}{4\pi\epsilon_0} \left[ \frac{1}{b^2} - \frac{R^2}{a^2b^2} \right] \hat{X} \)

Check Answer

Option 1

Q.No:26 CSIR Dec-2023

A one dimensional infinite long wire with uniform linear charge density \( \lambda \), is placed along the z-axis. The potential difference \( \delta V = V(\rho + a) - V(\rho) \), between two points at radial distances \( \rho + a \) and \( \rho \) from the z-axis, where \( a \ll \rho \), is closest to

1) \( -\frac{\lambda a^2}{2\pi\epsilon_0 \rho^2} \)

2) \( -\frac{\lambda a}{2\pi\epsilon_0 \rho} \)

3) \( \frac{\lambda a}{2\pi\epsilon_0 \rho} \)

4) \( \frac{\lambda a^2}{2\pi\epsilon_0 \rho^2} \)

Check Answer

Option 2

Q.No:27 CSIR June-2024

A two dimensional sheet with a uniform sheet conductivity of \(\sigma\) has a central metallic point contact and a circular metal contact at the boundary as shown in the figure.

If a constant current \(I\) is injected through the central contact and collected at the boundary, then the voltage difference between two points on the sheet at radius \(r_1\) and \(r_2\) is proportional to

1) \(\frac{I}{\sigma} \left[\tan^{-1} \left(\frac{r_2}{r_1}\right) - \frac{\pi}{4}\right]\)

2) \(\frac{I}{\sigma} \left[\ln \left(\frac{r_2}{r_1}\right)\right]\)

3) \(\frac{I}{\sigma} \left(\frac{r_2 - r_1}{r_2 + r_1}\right)\)

4) \(\frac{I}{\sigma} \left(\frac{r_2 - r_1}{r_2 + r_1}\right)^3\)

Check Answer

Option 2

Q.No:28 CSIR June-2024

The region \(y > 0\) has a constant electrostatic potential \(V_1\) and \(y < 0\) has a constant electrostatic potential \(V_2 \neq V_1\). A charged particle with momentum \(\vec{p}_1\) is incident at an angle \(\theta_1\) on the interface of the two regions (see figure below).

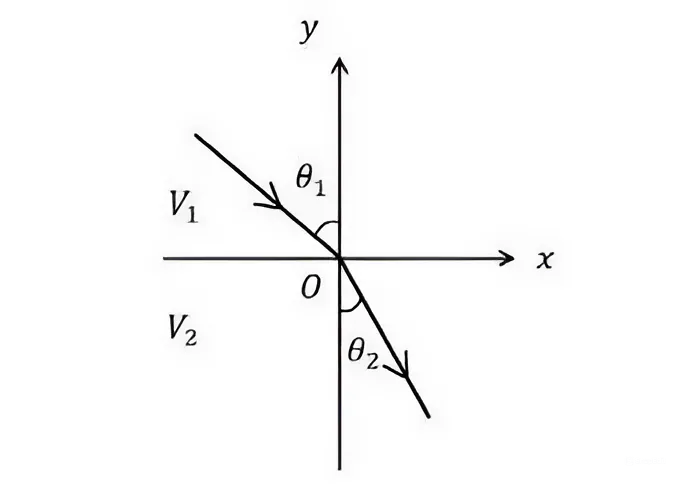
If the particle has momentum \(\vec{p}_2\) in the region \(y < 0\), then the angle \(\theta_2\) is given by

1) \(\cos^{-1} \left( \frac{p_2}{p_1} \cos \theta_1 \right)\)

2) \(\cos^{-1} \left( \frac{p_1}{p_2} \cos \theta_1 \right)\)

3) \(\sin^{-1} \left( \frac{p_2}{p_1} \sin \theta_1 \right)\)

4) \(\sin^{-1} \left( \frac{p_1}{p_2} \sin \theta_1 \right)\)

Check Answer

Option 4

Q.No:29 CSIR June-2024

A point electric dipole \(\vec{P} = p_x \hat{i}\) is placed at a vertical distance \(d\) above a grounded infinite conducting \(xy\) plane as shown in the figure.

At a point \(\vec{r}\) \((r \gg d, z > 0)\) far away from the dipole, the electrostatic potential \(V(r)\) varies approximately as

1) \(\frac{1}{r^2}\)

2) \(\frac{1}{r^6}\)

3) \(\frac{1}{r^3}\)

4) \(\frac{1}{r^4}\)

Check Answer

Option 3

Q.No:30 CSIR Dec-2024

A static charge distribution produces an electric field \[ \vec{E} = \frac{Q}{4\pi\epsilon_{0}}\, \frac{e^{-br}}{r^{3}}\, \vec{r}, \] where \(Q, b > 0\) are constants. The charge density of the distribution is given by

1) \(\frac{Q}{4\pi}\left[-\frac{b}{2r^{2}}\right]\)

2) \(\frac{Q}{4\pi}e^{-b}\left[-\frac{b}{r^{2}} - 4\pi\delta(\vec{r})\right]\)

3) \(\frac{Q}{4\pi}e^{-br}\left[-\frac{2b}{r^{2}}\right]\)

4) \(\frac{Q}{4\pi}e^{-br}\left[-\frac{b}{r^{2}} + 4\pi\delta(\vec{r})\right]\)

Check Answer

Option 4

Q.No:31 CSIR Dec-2024

Consider a spherical region of radius \( \frac{R}{2} \) centered at the origin of the coordinate system. Three point charges each of magnitude \(Q\) are placed at \((0,0,R)\), \((0,R,0)\) and \((\sqrt{2}R,0,0)\). What is the magnitude of the average electric field over the spherical region due to these charges in units of \( \frac{Q}{4\pi\epsilon_{0}R^{2}} \)?

1) \(\frac{3}{5}\)

2) \(0\)

3) \(\frac{5}{2}\)

4) \(\frac{3}{2}\)

Check Answer

Option 4

Q.No:32 CSIR June-2025

The charge density of the electron cloud of a hydrogen atom is given by \[ \rho(\vec{r}) = -\frac{e}{8\pi a^{3}} \exp\!\left(-\frac{r}{a}\right) \] where \(a\) is some characteristic length. The potential energy due to the interaction between the proton (sitting at the origin) and the electron cloud is given by

1) \(-\frac{e^{2}}{2\pi\epsilon_{0}a}\)

2) \(-\frac{e^{2}}{4\pi\epsilon_{0}a}\)

3) \(-\frac{e^{2}}{\pi\epsilon_{0}a}\)

4) \(-\frac{e^{2}}{8\pi\epsilon_{0}a}\)