Q.No:1 JAM-2015
A charge \(q\) is at the center of two concentric spheres. The outward electric flux through the inner
sphere is \(\phi\) while that through the outer sphere is \(2\phi\). The amount of charge contained in the region
between the two spheres is
(A)
\(2\hspace{0.3mm}q\)
(B)
\(q\)
(C)
\(-q\)
(D)
\(-2\hspace{0.3mm}q\)
Check Answer
Option B
Q.No:2 JAM-2015
A hollow, conducting spherical shell of inner radius \(R_1\) and outer radius \(R_2\) encloses a charge \(q\) inside, which is located at a distance \(d\)\((<R_1)\) from the centre of the spheres. The potential at the centre of the shell is
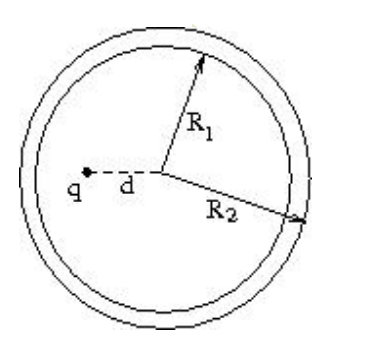
(A)
Zero
(B)
\(\frac{1}{4\pi\epsilon_0}\frac{q}{d}\)
(C)
\(\frac{1}{4\pi\epsilon_0}(\frac{q}{d}-\frac{q}{R_1})\)
(D)
\(\frac{1}{4\pi\epsilon_0}(\frac{q}{d}-\frac{q}{R_1}+\frac{q}{R_2})\)
Check Answer
Option D
Q.No:3 JAM-2016
For an infinitely long wire with uniform line-charge density,\(\lambda\), along the z-axis, the electric field at
a point (a,b,0) away from the origin is
\((\hat{e}_x, \hat{e}_y\) and \(\hat{e}_z\) are unit vectors in Cartesian−coordinate system.)
(A)
\(\frac{\lambda}{2\pi \epsilon_0\sqrt{a^2+b^2}}(\hat{e_x}+\hat{e_y})\)
(B)
\(\frac{\lambda}{2\pi \epsilon_0(a^2+b^2)}(a\hat{e_x}+b\hat{e_y})\)
(C)
\(\frac{\lambda}{2\pi \epsilon_0\sqrt{a^2+b^2}}\hat{e_x}\)
(D)
\(\frac{\lambda}{2\pi \epsilon_0\sqrt{a^2+b^2}}\hat{e_z}\)
Check Answer
Option B
Q.No:4 JAM-2016
An arbitrarily shaped conductor encloses a charge \(q\) and is surrounded by a conducting hollow sphere as shown in the figure. Four different regions of space, \(1,2,3,\) and \(4,\) are indicated in the figure. Which one of the following statements is correct?

(A)
The electric field lines in region \(2\) are not affected by the position of the charge \(q\).
(B)
The surface charge density on the inner wall of the hollow sphere is uniform.
(C)
The surface charge density on the outer surface of the sphere is always uniform irrespective of the position of charge \(q\) in region \(1\).
(D)
The electric field in region \(2\) has a radial symmetry.
Check Answer
Option C
Q.No:5 JAM-2016
For an electric dipole with moment \(\vec{p}=p_0 \hat{e}_z\) placed at the origin, (\(p_o\) is a constant of appropriate dimensions and \(\hat{e}_x, \hat{e}_y\) and \(\hat{e}_z\) are unit vectors in Cartesian−coordinate system.)
(A)
potential falls as \(\frac{1}{r^2}\), where \(r\) is the distance from origin.
(B)
a spherical surface centered at origin is an equipotential surface.
(C)
electric flux through a spherical surface enclosing the origin is zero.
(D)
radial component of \(\vec{E}\) is zero on the xy -plane.
Check Answer
Option A,C,D
Q.No:6 JAM-2016
The shape of a dielectric lamina is defined by the two curves \(y=0\) and \(y=1-x^2\). If the charge density of the lamina \(\sigma =15y\) \(C/m^2\), then the total charge on the lamina is ________________ \(C\).
Check Answer
Ans 8
Q.No:7 JAM-2017
For a point dipole of dipole moment \(\vec{p}=p\hat{z}\) located at the origin, which of the following is (are) correct?
(A)
The electric field at (0,b,0) is zero
(B)
The work done in moving a charge \(q\) from (0,b,0) to (0,0,b) is \(\frac{qp}{4\pi \epsilon_0 b^2}\)
(C)
The electrostatic potential at (b,0,0) is zero
(D)
If a charge q is kept at (0,0,b) it will exert a force of magnitude \(\frac{qp}{4\pi \epsilon_0 b^3}\) on the dipole
Check Answer
Option B,C
Q.No:8 JAM-2017
A dielectric sphere of radius \(R\) has constant polarization \(\vec{P}=P_0\hat{z}\) so that the field inside the sphere is \(\vec{E}_{in}=-\frac{P_0}{3\epsilon_0}\hat{z}\). Then, which of the following is (are) correct?
(A)
The bound surface charge density is \(P_0\) cos \(\theta\)
(B)
The electric field at a distance \(r\) on the z - axis varies as \(\frac{1}{r^2}\) for \(r\gg R\)
(C)
The electric potential at a distance \(2R\) on the z - axis is \(\frac{P_0 R}{12\epsilon_0}\)
(D)
The electric field outside is equivalent to that of a dipole at the origin
Check Answer
Option A,C,D
Q.No:9 JAM-2017
In a coaxial cable, the radius of the inner conductor is 2mm and that of the outer one is 5mm . The inner conductor is at a potential of 10V , while the outer conductor is grounded. The value of the potential at a distance of 3.5mm from the axis is ________________.
(Specify your answer in volts to two digits after the decimal point.)

Check Answer
Ans 3.79-3.99
Q.No:10 JAM-2017
A sphere of radius \(R\) has a uniform charge density \(\rho\). A sphere of smaller radius \(\frac{R}{2}\) is cut out from the original sphere, as shown in the figure below. The center of the cut out sphere lies at \(z=\frac{R}{2}\). After the smaller sphere has been cut out, the magnitude of the electric field at \(z=-\frac{R}{2}\) is \(\frac{\rho R}{n\epsilon_0}\). The value of the integer \(n\) is _______________.

Check Answer
Ans 8
Q.No:11 JAM-2018
Three infinite plane sheets carrying uniform charge densities \(-\sigma,2\sigma,3\sigma\) are placed parallel to the
x-z plane at \(y=a,3a,4a\), respectively. The electric field at the point (0,2a,0) is
(A)
\(\frac{4\sigma}{\epsilon_0}\hat{J}\)
(B)
\(-\frac{3\sigma}{\epsilon_0}\hat{J}\)
(C)
\(-\frac{2\sigma}{\epsilon_0}\hat{J}\)
(D)
\(\frac{\sigma}{\epsilon_0}\hat{J}\)
Check Answer
Option B
Q.No:12 JAM-2018
Given a spherically symmetric charge density
\[
\rho(r) =
\begin{cases}
k r^2, r < R\\
0, r \gt R
\end{cases}
\]
(k being a constant), the electric field for \(r<R\) is (take the total charge as \(Q\))
(A)
\(\frac{Qr^3}{4\pi \epsilon_0 R^5}\hat{r}\)
(B)
\(\frac{3Qr^2}{4\pi \epsilon_0 R^4}\hat{r}\)
(C)
\(\frac{5Qr^3}{8\pi \epsilon_0 R^5}\hat{r}\)
(D)
\(\frac{Q}{4\pi \epsilon_0 r^2}\hat{r}\)
Check Answer
Option A
Q.No:13 JAM-2018
Let the electric field in some region \(R\) be given by \(\vec{E}=e^{-y^2}\hat{i}+e^{-x^2}\hat{j}\). From this we may conclude that
(A)
\(R\) has a non-uniform charge distribution.
(B)
\(R\) has no charge distribution.
(C)
\(R\) has a time dependent magnetic field.
(D)
The energy flux in \(R\) is zero everywhere.
Check Answer
Option B,C
Q.No:14 JAM-2019
A small spherical ball having charge q and mass \(m\), is tied to a thin massless nonconducting string of length \(l\). The other end of the string is fixed to an infinitely extended
thin non-conducting sheet with uniform surface charge density \(\sigma\). Under equilibrium, the string makes an angle \(45^\circ \) with the sheet as shown in the figure. Then \(\sigma\) is given by
(g is the acceleration due to gravity and \(\epsilon_0\)
is the permittivity of free space)

(A)
\(\frac{mg\epsilon_0}{q}\)
(B)
\(\sqrt{2}\frac{mg\epsilon_0}{q}\)
(C)
\(2\frac{mg\epsilon_0}{q}\)
(D)
\(\frac{mg\epsilon_0}{q\sqrt{2}}\)
Check Answer
Option C
Q.No:15 JAM-2019
Out of the following statements, choose the correct option(s) about a perfect conductor.
(A)
The conductor has an equipotential surface
(B)
Net charge, if any, resides only on the surface of conductor
(C)
Electric field cannot exist inside the conductor
(D)
Just outside the conductor, the electric field is always perpendicular to its surface
Check Answer
Option A,B,C,D
Q.No:16 JAM-2019
The electrostatic energy (in units of \(\frac{1}{4\pi \epsilon_0}\) J) of a uniformly charged spherical shell of total
charge 5 C and radius 4 m is _______________.
(Round off to 3 decimal places)
Check Answer
Ans 3.124-3.126
Q.No:17 JAM-2019
An infinitely long very thin straight wire carries uniform line charge density \(8\pi \times 10^{-2} \)C/m. The magnitude of electric displacement vector at a point located 20 mm
away from the axis of the wire is ___________________ \(C/m^2\).
Check Answer
Ans 2
Q.No:18 JAM-2020
Two stationary point particles with equal and opposite charges are at some fixed distance from each
other. The points having zero electric potential lie on:
(A)
A sphere
(B)
A plane
(C)
A cylinder
(D)
Two parallel planes
Check Answer
Option B
Q.No:19 JAM-2020
Three point charges each carrying a charge \(q\) are placed on the vertices of an equilateral triangle of side \(L\). The electrostatic potential energy of the configuration is:
(A)
\(\frac{1}{4\pi\epsilon_0}\frac{q^2}{L}\)
(B)
\(\frac{2}{4\pi\epsilon_0}\frac{q^2}{L}\)
(C)
\(\frac{3}{4\pi\epsilon_0}\frac{q^2}{L}\)
(D)
\(\frac{1}{\pi\epsilon_0}\frac{q^2}{L}\)
Check Answer
Option C
Q.No:20 JAM-2020
A spherical dielectric shell with inner radius \(a \) and outer radius \(b\), has polarization \(\vec{P}=\frac{k}{r^2}\hat{r}\),where
\(k\) is a constant and \(\hat{r}\) is the unit vector along the radial direction. Which of the following statements is/are correct?
(A)
The surface density of bound charges on the inner and outer surfaces are \(-k\) and \(+k\), respectively. The volume density of bound charges inside the dielectric is zero.
(B)
The surface density of bound charges is zero on both the inner and outer surfaces. The volume density of bound charges inside the dielectric is \(+k\)
(C)
The surface density of bound charges on the inner and outer surfaces are \(\frac{-k}{a^2}\) and \(\frac{k}{b^2}\), respectively. The volume density of bound charges inside the dielectric is zero.
(D)
The surface density of bound charges is zero on both the inner and outer surfaces. The volume density of bound charges inside the dielectric is \(\frac{3k}{4\pi(b^3-a^3)}\)
Check Answer
Option C
Q.No:21 JAM-2021
The total charge contained within the cube (see figure), in which the electric field is given by \(\vec{E}=K(4x^2 \hat{i}+3y\hat{j})\), where \(\epsilon_0\) is the permittivity of free space, is

(A)
\(7 K \epsilon_0\)
(B)
\(5 K \epsilon_0\)
(C)
\(3 K \epsilon_0\)
(D)
Zero
Check Answer
Option A
Q.No:22 JAM-2021
Four charges are placed very close to each other, as shown. The separation between the two charges on the y-axis is \(a\). The separation between the two charges on the x-axis is also \(a\). The leading order (non-vanishing) form of the electrostatic potential, at point \(P\), at a distance \(r\) from the origin \((r \gg a)\), is
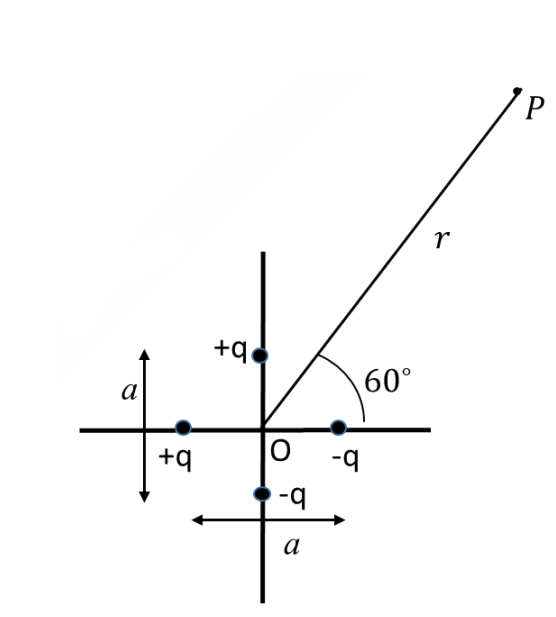
(A)
\(\frac{1}{4\pi \epsilon_0}\frac{qa}{2r^2}(\sqrt{3}-1)\)
(B)
\(\frac{1}{4\pi \epsilon_0}\frac{2qa}{r^2}\)
(C)
\(\frac{1}{4\pi \epsilon_0}\frac{qa}{r^2}(\sqrt{5}-1)\)
(D)
\(\frac{1}{4\pi \epsilon_0}\frac{qa}{r^2}(1-\sqrt{3})\)
Check Answer
Option A
Q.No:23 JAM-2022
Consider an electrostatic field \(\vec{E}\) in a region of space. Identify the \(\textbf{INCORRECT}\) statement.
(A)
The work done in moving a charge in a closed path inside the region is zero
(B)
The curl of \(\vec{E}\) is zero
(C)
The field can be expressed as the gradient of a scalar potential
(D)
The potential difference between any two points in the region is always zero
Check Answer
Option D
Q.No:24 JAM-2022
The work done in moving a \(-5\mu C\) charge in an electric field \(\vec{E}=(8r \hspace{1.5mm} sin \hspace{1.5mm} \theta \hspace{1.5mm} \hat{r}+ 4r \hspace{1.5mm} cos \hspace{1.5mm} \theta \hat{\theta})\) V/m, from a point \(A(r,\theta)=(10, \frac{\pi}{6})\) to a point \(B(r,\theta)=(10, \frac{\pi}{2})\), is _________________ mJ.
Check Answer
Ans (-1) OR 1
Q.No:25 JAM-2022
A charge \(q\) is uniformly distributed over the volume of a dielectric sphere of radius \(a\). If the dielectric constant \(\epsilon_r =2\), then the ratio of the electrostatic energy stored inside the sphere to that stored outside is __________________ (Round off to 1 decimal place).
Check Answer
Ans 0.1
Q.No:26 JAM-2023
A metallic sphere of radius \(R\) is held at electrostatic potential \(V\). It is enclosed in a concentric thin metallic shell of radius \(2R\) at potential \(2V\). If the potential at the distance \(\frac{3}{2} R\) from the centre of the sphere is \(fV \), then the value of \(f\) is _________ (rounded off to two decimal places).
Check Answer
Ans 1.64-1.70
Q.No:27 JAM-2023
At the planar interface of two dielectrics, which of the following statements related to the electric field (\(\vec{E}\)), electric displacement (\(\vec{D}\)) and polarization (\(\vec{P}\)) is true?
A) Normal component of both \(\vec{D}\) and \(\vec{P}\) are continuous
B) Normal component of both \(\vec{D}\) and \(\vec{E}\) are discontinuous
C) Normal component of \(\vec{D}\) is continuous and that of \(\vec{P}\) is discontinuous
D) Normal component of both \(\vec{E}\) and \(\vec{P}\) are continuous
Check Answer
Option C
Q.No:28 JAM-2024
A vector field is expressed in the cylindrical coordinate system \((s, \phi, z)\) as,
\[
\vec{F} = \frac{A}{s} \hat{s} + \frac{B}{s} \hat{z}.
\]
If this field represents an electrostatic field, then the possible values of \(A\) and \(B\), respectively, are:
A) 1 and 0
B) 0 and 1
C) -1 and 1
D) 1 and -1
Check Answer
Option A
Q.No:29 JAM-2024
The plane \( z = 0 \) separates two linear dielectric media with relative permittivities \( \varepsilon_{r1} = 4 \) and \( \varepsilon_{r2} = 3 \), respectively. There is no free charge at the interface. If the electric field in the medium 1 is \( \vec{E}_1 = 3\hat{x} + 2\hat{y} + 4\hat{z} \), then the displacement vector \( \vec{D}_2 \) in medium 2 is:
(\( \varepsilon_0 \) is the permittivity of free space)
A) \( (3\hat{x} + 4\hat{y} + 6\hat{z})\varepsilon_0 \)
B) \( (3\hat{x} + 6\hat{y} + 8\hat{z})\varepsilon_0 \)
C) \( (9\hat{x} + 6\hat{y} + 16\hat{z})\varepsilon_0 \)
D) \( (4\hat{x} + 2\hat{y} + 3\hat{z})\varepsilon_0 \)
Check Answer
Option C
Q.No:30 JAM-2024
A charge of \( -9C \) is placed at the center of a concentric spherical shell made of a linear dielectric material (relative permittivity 9) and having inner and outer radii of \( 0.1m \) and \( 0.2m \), respectively. The total charge induced on its inner surface is __________C. (Rounded off to two decimal places)
Check Answer
Ans 7.90-8.10
Q.No:31 JAM-2024
Two positive charges \( Q \) and \( 2Q \) are kept at points \( A \) and \( B \), separated by a distance \( 2d \), as shown in the figure. \( MCL \) is a semicircle of radius \( 2d \) centered at the origin \( O \). If \( Q = 2C \) and \( d = 10cm \), the value of the line integral \( \int_{M}^{L} \mathbf{E} \cdot d\mathbf{l} \) (where \( \mathbf{E} \) represents electric field) along the path \( MCL \) will be ______________ \( V \).
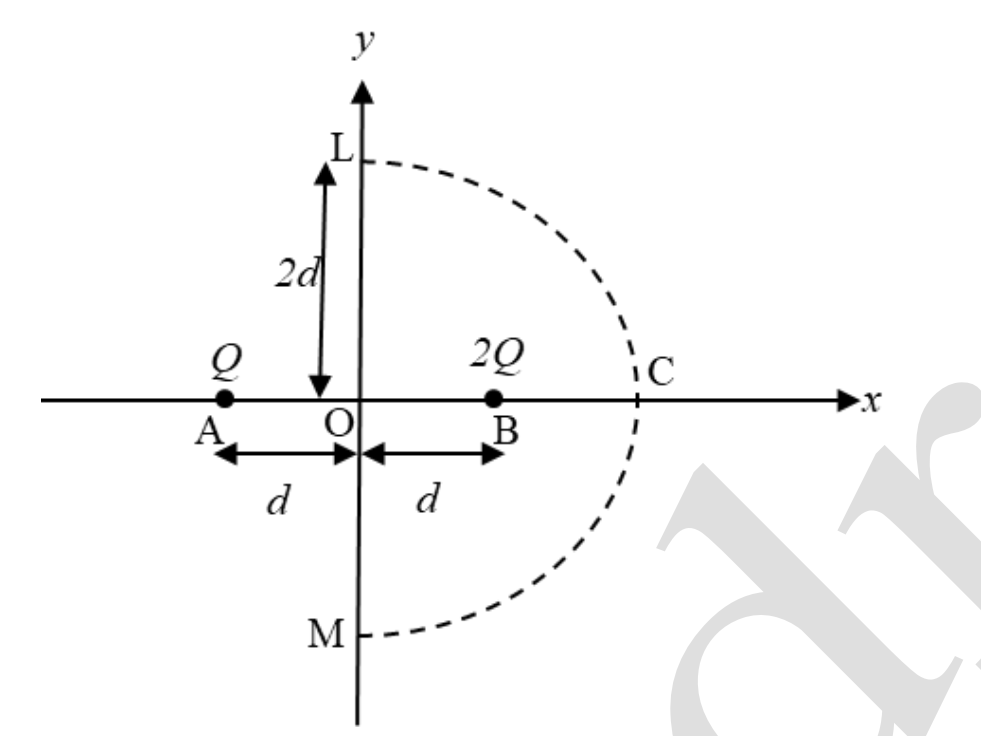
Check Answer
Ans 0
Q.No:32 JAM-2025
A charge \(q\) is placed at the centre of the base of a square pyramid.
The net outward electric flux across each of the slanted faces is ______.
(Consider permittivity as \(\varepsilon_0\))

A) \(\frac{q}{\varepsilon_0}\)
B) \(\frac{q}{2\varepsilon_0}\)
C) \(\frac{q}{4\varepsilon_0}\)
D) \(\frac{q}{8\varepsilon_0}\)
Check Answer
Option D
Q.No:33 JAM-2025
Consider a parallel plate capacitor (distance between the plates \(d\),
permittivity \(\varepsilon_0\)) as shown.
The space charge density between the plates varies as
\[
\rho(x) = \rho_0 e^{-x}.
\]
The voltage \(V = 0\) at both \(x = 0\) and \(x = d\).
The voltage \(V(x)\) at a point \(P\) between the plates is
[\(\rho_0\) is a constant of appropriate dimensions]

A) \(
\frac{\rho_0}{\varepsilon_0}
\left[
e^{-x}
+
\frac{1 - e^{-d}}{d}x
-1
\right]
\)
B) \(
\frac{2\rho_0}{\varepsilon_0}
\left[
e^{-x}
+
\frac{1 - e^{-d}}{d}x
-1
\right]
\)
C) \(
\frac{\rho_0}{2\varepsilon_0}
\left[
e^{-x}
+
\frac{1 - e^{-d}}{d}x
-1
\right]
\)
D) \(
\frac{3\rho_0}{\varepsilon_0}
\left[
e^{-x}
+
\frac{1 - e^{-d}}{d}x
-1
\right]
\)
Check Answer
Option A
Q.No:33 JAM-2025
Consider a metal sphere enclosed concentrically within a spherical shell.
The inner sphere of radius \(a\) carries charge \(Q\).
The outer shell of radius \(2a\) also has charge \(Q\).
The variation of the magnitude \(E\) of the electric field as a function
of distance \(r\) from the center \(O\) is
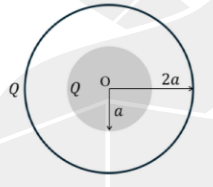
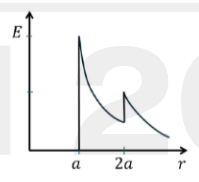


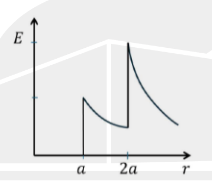
Check Answer
Option A
Q.No:34 JAM-2025
A spherical ball having a uniformly distributed charge \(Q\) and radius \(R\)
pulsates with frequency \(\omega\) such that the radius changes by \(\pm 10\%\),
as shown in the figure.
Which of the following is(are) correct?
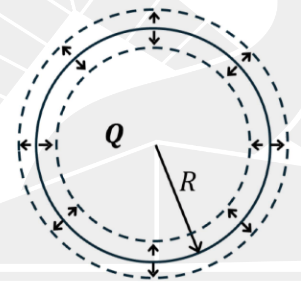
A) The net outward electric flux across a spherical surface
of radius r > 1.5R pulsates with frequency ω
B) The net outward electric flux across a spherical surface
of radius r = 2R is \(\frac{Q}{\varepsilon_0}\)
C) The potential fluctuates with frequency \(\omega\) at r = 2R
D) The electric field inside the sphere at r = 0.5R
will not be time dependent
Check Answer
Option B
Q.No:35 JAM-2025
Which of the following relations is(are) valid for linear dielectrics?
[E = Electric field,
P = Polarization,
D = Electric displacement,
\(\epsilon\) = Permittivity of free space,
\(\epsilon_0\) = Dielectric permittivity,
\(\chi_e\) = Electric susceptibility,
\(\rho_f\) = Free charge density,
\(\rho_b\) = Bound charge density]
A) \(
\mathbf{P} = \varepsilon_0 \chi_e \mathbf{E}
\)
B) \(
\varepsilon = \varepsilon_0 (1 + \chi_e)
\)
C) \(
\mathbf{D} = \varepsilon_0 \mathbf{E} + \mathbf{P}
\)
D) \(
\nabla \cdot \mathbf{D} = \rho_f + \rho_b
\)
Check Answer
Option A,B,C
Q.No:36 JAM-2025
Consider two media 1 and 2 having permittivities
\(\varepsilon_0\) and \(\varepsilon_1 (= 2\varepsilon_0)\), respectively.
The interface between the two media aligns with the x–y plane.
An electric field
\[
\vec{E}_1 = 4\hat{i} - 5\hat{j} - \hat{k}
\]
exists in medium 1.
The magnitude of the displacement vector \(\vec{D}_2\) in medium 2 is
______ \(\varepsilon_0\). (up to two decimal places)

Q.No.1 Discussion :
Q.No.2 Discussion :
Q.No.3 Discussion :
Q.No.4 Discussion :
Q.No.5 Discussion :
Q.No.6 Discussion :
Q.No.7 Discussion :
Q.No.8 Discussion :
Q.No.9 Discussion :
Q.No.10 Discussion :
Q.No.11 Discussion :
Q.No.12 Discussion :
Q.No.13 Discussion :
Q.No.14 Discussion :
Q.No.15 Discussion :
Q.No.16 Discussion :
Q.No.17 Discussion :
Q.No.18 Discussion :
Q.No.19 Discussion :
Q.No.20 Discussion :
Q.No.21 Discussion :
Q.No.22 Discussion :
Q.No.23 Discussion :
Q.No.24 Discussion :
Q.No.25 Discussion :