Electrostatics JEST - S. N. Bose Physics Learning Center

Q.No:1 JEST-2012

An electric field in a region is given by \(\vec{E}(x, y, z)=ax\hat{i}+cz\hat{j}+6by\hat{k}\). For which values of \(a, b, c\) does this represent an electrostatic field?

(a) \(13, 1, 12\)

(b) \(17, 6, 1\)

(d) \(45, 6, 1\)

Check Answer

Option c

Q.No:2 JEST-2012

Consider a particle of electric charge \(e\) and mass \(m\) moving under the influence of a constant horizontal electric field \(E\) and constant vertical gravitational field described by acceleration due to gravity \(g\). If the particle starts from rest, what will be its trajectory?

(a) parabolic

(b) elliptic

(d) circular

Check Answer

Option c

Q.No:3 JEST-2012

A point charge \(+q\) is placed at \((0, 0, d)\) above a grounded infinite conducting plane defined by \(z=0\). There are no charges present anywhere else. What is the magnitude of electric field at \((0, 0, −d)\)?

(a) \(q/(8\pi \epsilon_0 d^2)\)

(b) \(-\infty\)

(d) \(q/(16\pi \epsilon_0 d^2)\)

Check Answer

Option c

Q.No:4 JEST-2012

A cube has a constant electric potential \(V\) on its surface. If there are no charges inside the cube, the potential at the center of the cube is

(a) \(V\)

(b) \(V/8\)

(d) \(V/6\)

Check Answer

Option a

Q.No:5 JEST-2013

The electric fields outside \((r>R)\) and inside (r>R) a solid sphere with a uniform volume charge density are given by \(\vec{E}_{r>R}\)=\(\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\hat{r}\) and \(\vec{E}_{rR}=\frac{1}{4\pi \epsilon_0}\frac{q}{r^2}\hat{r}\), \(q\) being the total charge. The correct ratio of the electrostatic energies for the second case to the first case is \(\vec{E}_{r>R}\)=\(\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\hat{r}\) and \(\vec{E}_{rR}=\frac{1}{4\pi \epsilon_0}\frac{q}{r^2}\hat{r}\), \(q\) being the total charge. The correct ratio of the electrostatic energies for the second case to the first case is

(a) \(1:3\)

(b) \(9:16\)

(d) \(5:6\)

Check Answer

Option d

Q.No:6 JEST-2013

If \(\vec{E}_1=xy\hat{i}+2yz\hat{j}+3xz\hat{k}\) and \(\vec{E}_2=y^2\hat{i}+(2xy+z^2)\hat{j}+2yz\hat{k}\) then

(a) Both are impossible electrostatic fields.

(b) Both are possible electrostatic fields.

(d) \(\vec{E}_2\) is a possible electrostatic field.

Check Answer

Option d

Q.No:7 JEST-2013

A charge \(q\) is placed at the centre of an otherwise neutral dielectric sphere of radius \(a\) and relative permittivity \(\epsilon_r\). We denote the expression \(q/4\pi \epsilon_0 r^2\) by \(E(r)\). Which of the following statements is \({\bf false}\)?

(a) The electric field inside the sphere, \(r<a\), is given by \(E(r)/\epsilon_r\).

(b) The field outside the sphere, \(r>a\), is given by \(E(r)\).

(d) The total charge inside a sphere of radius \(r<a\) is given by \(q\).

Check Answer

Option d

Q.No:8 JEST-2014

Two large nonconducting sheets one with a fixed uniform positive charge and another with a fixed uniform negative charge are placed at a distance of \(1\) meter from each other. The magnitude of the surface charge densities are \(\sigma_+=6.8 \mu C/m^2\) for the positively charged sheet and \(\sigma_{-}=4.3 \mu C/m^2\) for the negatively charged sheet. What is the electric field in the region between the sheets?

(a) \(6.30\times 10^5 N/C\)

(b) \(3.84\times 10^5 N/C\)

(d) \(1.16\times 10^5 N/C\)

Check Answer

Option a

Q.No:9 JEST-2014

A conducting sphere of radius \(r\) has charge \(Q\) on its surface. If the charge on the sphere is doubled and its radius is halved, the energy associated with the electric field will

(a) increase four times

(b) increase eight times

(d) decrease four times

Check Answer

Option b

Q.No:10 JEST-2015

A circular loop of radius \(R\), carries a uniform line charge density \(\lambda\). The electric field, calculated at a distance \(z\) directly above the center of the loop, is maximum if \(z\) is equal to

(a) \(\frac{R}{\sqrt{3}}\)

(b) \(\frac{R}{\sqrt{2}}\)

(d) \(2R\)

Check Answer

Option b

Q.No:11 JEST-2015

Consider two point charges \(q\) and \(\lambda q\) located at the points, \(x=a\) and \(x=\mu a\), respectively. Assuming that the sum of the two charges is constant, what is the value of \(\lambda\) for which the magnitude of the electrostatic force is maximum?

(a) \(\mu\)

(b) \(1\)

(d) \(1+\mu\)

Check Answer

Option b

Q.No:12 JEST-2015

A spherical shell of inner and outer radii \(a\) and \(b\), respectively, is made of a dielectric material with frozen polarization \(\vec{P}(r)=\frac{k}{r}\hat{r}\), where \(k\) is a constant and \(r\) is the distance from the its centre. The electric field in the region \(a<r<b\) is,

(a) \(\vec{E}=\frac{k}{\in_0 r}\hat{r}\)

(b) \(\vec{E}=-\frac{k}{\in_0 r}\hat{r}\)

(d) \(\vec{E}=\frac{k}{\in_0 r^2}\hat{r}\)

Check Answer

Option b

Q.No:13 JEST-2015

The electrostatic potential due to a charge distribution is given by \(V(r)=A\frac{e^{-\lambda r}}{r}\) where \(A\) and \(\lambda\) are constants. The total charge enclosed within a sphere of radius \(\frac{1}{\lambda}\), with its origin at \(r=0\) is given by,

(a) \(\frac{8\pi \in_0 A}{e}\)

(b) \(\frac{4\pi \in_0 A}{e}\)

(d) \(0\)

Check Answer

Option a

Q.No:14 JEST-2016

A point charge \(q\) of mass \(m\) is released from rest at a distanced from an infinite grounded conducting plane (ignore gravity). How long does it take for the charge to hit the plane?

(A) \(\frac{\sqrt{2\pi^3 \epsilon_0 md^3}}{q}\)

(B) \(\frac{\sqrt{2\pi^3 \epsilon_0 md}}{q}\)

(D) \(\frac{\sqrt{\pi^3 \epsilon_0 md}}{q}\)

Check Answer

Option A

Q.No:15 JEST-2016

Suppose \(yz\) plane forms the boundary between two linear dielectric media \(I\) and \(II\) with dielectric constant \(\epsilon_I=3\) and \(\epsilon_{II}=4\), respectively. If the electric field in region \(I\) at the interface is given by \(\vec{E}_I=4\hat{x}+3\hat{y}+5\hat{z}\), then the electric field \(\vec{E}_{II}\) at the interface in region \(II\) is:

(A) \(4\hat{x}+3\hat{y}+5\hat{z}\)

(B) \(4\hat{x}+0.75\hat{y}-1.25\hat{z}\)

(D) \(3\hat{x}+3\hat{y}+5\hat{z}\)

Check Answer

Option D

Q.No:16 JEST-2017

Two equal positive charges of magnitude \(+q\) separated by a uniformly charged thin spherical shell of radius \(2d\) bearing a total charge \(-2q\) and centred at the midpoint between the two positive charges. The net electric field at distance \(r\) from the midpoint (\(\gg d\)) is

(A) zero.

(B) proportional to \(d\).

(D) proportional to \(1/r^4\).

Check Answer

Option D

Q.No:17 JEST-2017

A sphere of inner radius \(1 cm\) and outer radius \(2 cm\), centered at origin has a volume charge density \(\rho_0=\frac{K}{4\pi r}\), where \(K\) is a nonzero constant and \(r\) is the radial distance. A point charge of magnitude \(10^{-3} C\) is placed at the origin. For what value of \(K\) in units of \(C/m^2\), the electric field inside the shell is constant?

Check Answer

Ans 20

Q.No:18 JEST-2017

A solid, insulating sphere of radius \(1 cm\) has charge \(10^{-7} C\) distributed uniformly over its volume. It is surrounded concentrically by a conducting thick spherical shell of inner radius \(2 cm\), outer radius \(2.5 cm\) and is charged with \(-2\times 10^{-7} C\). What is the electrostatic potential in Volts on the surface of the sphere?

Check Answer

Ans 9000

Q.No:19 JEST-2017

For an electric field \(\vec{E}=k\sqrt{x}\hat{x}\) where \(k\) is a non-zero constant, total charge enclosed by the cube as shown below is

(A) \(0\)

(B) \(k\epsilon_0 l^{5/2} (\sqrt{3}-1)\).

(D) \(k\epsilon_0 l^{5/2} (\sqrt{2}-1)\).

Check Answer

Option D

Q.No:20 JEST-2017

Consider a grounded conducting plane which is infinitely extended perpendicular to the \(y\)-axis at \(y=0\). If an infinite line of charge per unit length \(\lambda\) runs parallel to \(x\)-axis at \(y=d\), then surface charge density on the conducting plane is

(A) \(\frac{-\lambda d}{(x^2+d^2+z^2)}\).

(B) \(\frac{-\lambda d}{(x^2+d^2+z^2)}\).

(D) \(\frac{-\lambda d}{2\pi(x^2+d^2+z^2)}\).

Check Answer

Option C

Q.No:21 JEST-2018

Two dielectric spheres of radius \(R\) are separated by a distance \(a\) such that \(a\gg R\). One of the spheres (sphere 1) has a charge \(q\) and the other is neutral. If the linear dimensions of the systems are scaled up by a factor two, by what factor should be change on the sphere 1 be changed so that the force between the two spheres remain unchanged?

(A) \(2\)

(B) \(4\sqrt{2}\)

(D) \(2\sqrt{2}\)

Check Answer

Option

Q.No:22 JEST-2018

An electric charge distribution produces an electric field \[ \vec{E}=(1-e^{-\alpha r})\frac{\vec{r}}{r^3}, \] where \(\delta\) and \(\alpha\) are constants. The net charge within a sphere of radius \(\alpha^{-1}\) centered at the origin is

(A) \(4\pi \epsilon_0(1-e^{-1})\)

(B) \(4\pi \epsilon_0(1+e^{-1})\)

(D) \(4\pi \epsilon_0 \frac{1}{\alpha e}\)

Check Answer

Option A

Q.No:23 JEST-2018

The charge density as a function of the radial distance \(r\) is given by \[ \rho(r)=\rho_0\frac{R^2-r^2}{R^2} \] for \(r<R\) and zero otherwise. The electric flux over the surface of an ellipsoid with axes \(3R, 4R\) and \(5R\) centered at the origin is

(A) \(\frac{4}{3\epsilon_0}\pi \rho_0 R^3\)

(B) \(\frac{8}{9\epsilon_0}\pi \rho_0 R^3\)

(D) zero

Check Answer

Option C

Q.No:24 JEST-2019

Consider two concentric spherical metal shells of radii \(r_1\) and \(r_2\) (\(r_2>r_1\)). The outer shell has a charge \(q\) and the inner shell is grounded. What is the charge on the inner shell?

(A) \(-\frac{r_1}{r_2}q\)

(B) \(\frac{r_1}{r_2}q\)

(D) \(\frac{r_2}{r_1}q\)

Check Answer

Option A

Q.No:25 JEST-2020

A ring of radius \(0.5 m\) has a gap of \(0.002\pi m\). If the ring carries a charge of \(+1.0 C\) distributed uniformly along it, then the electric field at the centre of the ring is

(A) \(7.5\times 10^7 NC^{-1}\)

(B) \(7.2\times 10^7 NC^{-1}\)

(D) \(6.5\times 10^7 NC^{-1}\)

Check Answer

Option B

Q.No:26 JEST-2020

Charges are placed as follows: \(q\) at \((a, a, 0)\) and \((-a, -a, 0)\), and \(-q\) at \((a, -a, 0)\) and \((-a, a, 0)\). At large distances, how does the electrostatic potential behave as a function of the distance \(r\) from the centre \((0, 0, 0)\)?

(A) \(1/r^3\)

(B) \(1/r^2\)

(D) \(1/r^4\)

Check Answer

Option A

Q.No:27 JEST-2021

Consider a spherical shell of radius \(R\) having a uniform surface charge density \(\sigma\). Suppose we construct a spherical Gaussian surface having the same radius \(R\) but its centre shifted from the charged sphere by a distance \(R\) (see the figure). What is the total electric flux \(\oint \vec{E}\cdot d\vec{A}\) through the Gaussian surface?

(A) \(0\)

(B) \(\pi R^2\sigma\)

(D) \(4\pi R^2\sigma\)

Check Answer

Option B

Q.No:28 JEST-2021

Assume the earth to be an uniform sphere of radius \(6400 \text{km}\) and having a uniform electric permittivity of \(8.85\times 10^{-12} \text{Farad/m}\). What would be the self capacitance (in micro-Farads) of the earth? Round off your answer to the nearest integer.

Check Answer

Ans 712

Q.No:29 JEST-2022

A conducting sphere of radius \(R\) is placed in a uniform electric field \(E_0\) directed along \(+z\) axis. The electric potential for outside points is given by \(V_{\text{out}}=-E_0(1-(R/r)^3)r\cos{\theta}\), where \(r\) is the distance from the center and \(\theta\) is the polar angle. The charge density on the surface of the sphere is

(a) \(3\epsilon_0 E_0 \cos{\theta}\)

(b) \(\epsilon_0 E_0 \cos{\theta}\)

(d) \(\frac{1}{3}\epsilon_0 E_0 \cos{\theta}\)

Check Answer

Option a

Q.No:30 JEST-2022

A point charge \(q\) is kept \(d\) distance above an infinite conducting plane. What is the energy stored in the configuration?

(a) \(-\frac{1}{4\pi\epsilon_0}\frac{q^2}{4d}\)

(b) \(-\frac{1}{4\pi\epsilon_0}\frac{q^2}{2d}\)

(d) \(\frac{1}{4\pi\epsilon_0}\frac{q^2}{4d}\)

Check Answer

Option a

Q.No:31 JEST-2022

Two point charges \(2q\) and \(q\) are placed inside two spherical cavities of equal radii \(R/4\) in a solid conducting sphere of radius \(R\), as shown in the figure. The cavities are placed along a diagonal at distances \(R/2\) from the center of the solid sphere. The electrical potential at a point \(P, 3R/2\) distance away from the center along the same diagonal, is given by

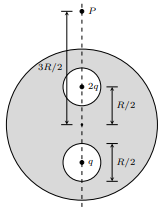
(a) \(\frac{1}{4\pi\epsilon_0}\frac{2q}{R}\)

(b) \(\frac{1}{4\pi\epsilon_0}\frac{5q}{2R}\)

(d) \(\frac{1}{4\pi\epsilon_0}\frac{3q}{R}\)

Check Answer

Option a

Q.No:32 JEST-2022

A point charge \(q\) is fixed at point \(A\) inside a hollow grounded conducting spherical shell of radius \(R\), at a distance \(a\) from the center \(C\). The force on the sphere due to the presence of the point charge is

(a) \(\frac{1}{4\pi \epsilon_0}\frac{q^2 aR}{(R+a)^2 (R-a)^2}\) in magnitude and along \(\overrightarrow{AC}\).

(b) \(\frac{1}{4\pi \epsilon_0}\frac{q^2 aR}{(R+a)^2 (R-a)^2}\) in magnitude and along \(\overrightarrow{CA}\).

(d) \(\frac{1}{4\pi \epsilon_0}\frac{q^2}{(R-a)^2}\) in magnitude and along \(\overrightarrow{CA}\).

Check Answer

Option a

Q.No:33 JEST-2022

A rectangular dielectric slab partly fills two identical rectangular parallel plate capacitors which are maintained at potentials \(V_1\) and \(V_2\) with \(V_1>V_2\). The slab can freely move in the space between the capacitor plates without any friction. Which of the following is true?

(a) The slab will move towards higher potential.

(b) The slab will move towards lower potential.

(d) The slab will position itself at \(1/V_1:1/V_2\) ratio between capacitors \(1\) and \(2\)

Check Answer

Option a

Q.No:34 JEST-2023

A point charge \(q\) is located at the apex of a cone of height \(h\) and base radius \(h\). The flux of the electric field through the cone due to the point charge is

(a) \((1-\frac{1}{\sqrt{2}}) \frac{q}{2\pi \epsilon_0}\)

(b) \((1-\frac{1}{\sqrt{2}}) \frac{ \pi q}{2 \epsilon_0}\)

(d) \((1-\frac{1}{\sqrt{2}}) \frac{q}{2 \epsilon_0}\)

Check Answer

Option d

Q.No:35 JEST-2023

A conducting spherical soap bubble of radius \(R\) with a wall thickness of \(W (\ll R)\) is charged to a potential of \(V_0\). The bubble bursts and becomes a spherical drop with potential \(V_d\). Select the correct value of the ratio \[\eta =\frac{V_d ^3 W}{V_0 ^3 R}.\]

(a) \(\frac{1}{3}\)

(b) \(\frac{1}{6}\)

(d) \(\frac{2}{3}\)

Check Answer

Option a

Q.No:36 JEST-2023

Calculate the magnitude of the force experienced by a point charge \(+q\) placed at a distance \(d\) from the center of a grounded conducting sphere of radius \(a (< d)\).

(a) \(\frac{q^2 ad}{ 4 \pi \epsilon_0 (d^2-a^2)^2}\)

(b) \(\frac{q^2 }{ 4 \pi \epsilon_0 (d-a)^2}\)

(d) \(0\)

Check Answer

Option a

Q.No:37 JEST-2024

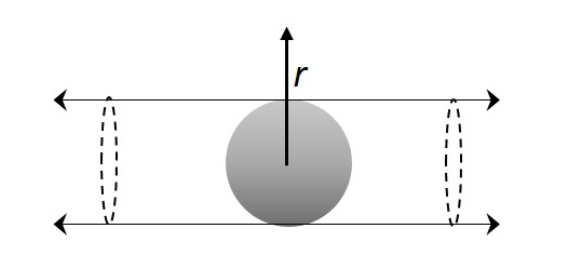
An infinitely long cylinder of radius \( R \) has uniform volume charge density. A spherical region of radius \( R \) is carved out of it, as shown in the figure. At what value of \( r \) (the radial coordinate in a cylindrical system, with origin at the center of the sphere) is the electric field maximum?

(a) \( r = \frac{4}{3}R \)

(b) \( r = R \)

(d) \( r = \frac{3}{2}R \)

Check Answer

Option a

Q.No:38 JEST-2024

A solid sphere of radius \( R \) has a volume charge density \( \rho = \rho_0 \sin 2\theta \). How does the leading term in the electrostatic potential depend on the distance \( r \) far away from the charged sphere?

(a) \(\frac{1}{r^2}\)

(b) \(\frac{1}{r}\)

(d) Does not depend on \( r \)

Check Answer

Option a

Q.No:39 JEST-2024

Three equal charges \( +q \) are placed at the corners of an equilateral triangle. A test charge constrained to move on the plane of the triangle is placed at the center of the triangle. Which of the following statements about the test charge is true?

(a) Stability of the equilibrium depends on the sign of the test charge.

(b) It is in a stable equilibrium.

(d) It is in an unstable equilibrium.

Check Answer

Option a

Q.No:40 JEST-2025

The electric dipole moment of a charge distribution is independent of the choice of the origin of coordinates only if

a) there is no magnetic field present.

b) the charge distribution is not time–dependent.

c) the total charge adds up to zero.

d) the charge distribution is discrete.

Check Answer

Option c

Q.No:41 JEST-2025

Consider two identical charged balls, each of mass \(m\) and charge \(q\). One of them is initially held fixed on a frictionless insulating horizontal surface and the other is carefully placed above the first one at a height \(h\) from the surface, such that the gravitational force on it is balanced by the Coulomb repulsion. The upper ball is now shifted horizontally by a distance \(d\,(d\ll h)\) to the right and then both balls are released. Which way will the balls move immediately after this?

a) ball on the surface moves towards right and ball above moves upwards.

b) both balls remain static at their new positions.

c) ball on the surface moves towards left, ball above moves downwards.

d) both balls oscillate around their original positions.

Check Answer

Option c

Q.No:42 JEST-2025

The time averaged electrostatic potential of a neutral H–atom is given by \[ \Phi(\vec{r})=\frac{q}{4\pi\epsilon_{0}}\frac{e^{-\alpha r}}{r}\left(1+\frac{\alpha r}{2}\right). \] The classical charge distribution corresponding to this is

a) \(-\,\frac{q}{8\pi}\alpha^{3}e^{-\alpha r}+q\delta^{3}(\vec{r})\)

b)\(-\,\frac{q}{8\pi}\alpha^{3}e^{-\alpha r}\)

c) \(q e^{-\alpha r}\left(1+\frac{\alpha r}{2}\right)\)

d) \(\frac{q}{8\pi}\alpha^{3}e^{-\alpha r}\left(1+\frac{\alpha r}{2}\right)-q\delta^{3}(\vec{r})\)

Check Answer

Option a

Q.No:43 JEST-2025

A simple pendulum with effective length \(l\) and a bob of mass \(m\) has a time period \(T_{1}\). Suppose now that the bob is given an electric charge \(+Q\). It is made to oscillate just above a two–dimensional infinite sheet with surface charge density \(+\sigma\), where \[ \frac{Q\sigma}{m g \epsilon_{0}}=\frac{3}{2}, \] \(\epsilon_{0}\) being the permittivity of free space and \(g\) the acceleration due to gravity. If the period of oscillation in this case is \(T_{2}\), determine \(\frac{T_{2}}{T_{1}}\) (neglect radiation from the charge). The value of \(\frac{T_{2}}{T_{1}}\) is _____