Numerical Questions
Q.No: 33
In the vector model of angular momentum applied to atoms, what is the minimum angle in degrees (in integer) made by the orbital angular momentum vector and the positive z axis for a \(2p\) electron?
Solution :
\(l=1, \hspace{3mm} m_l=-1,0,+1\)
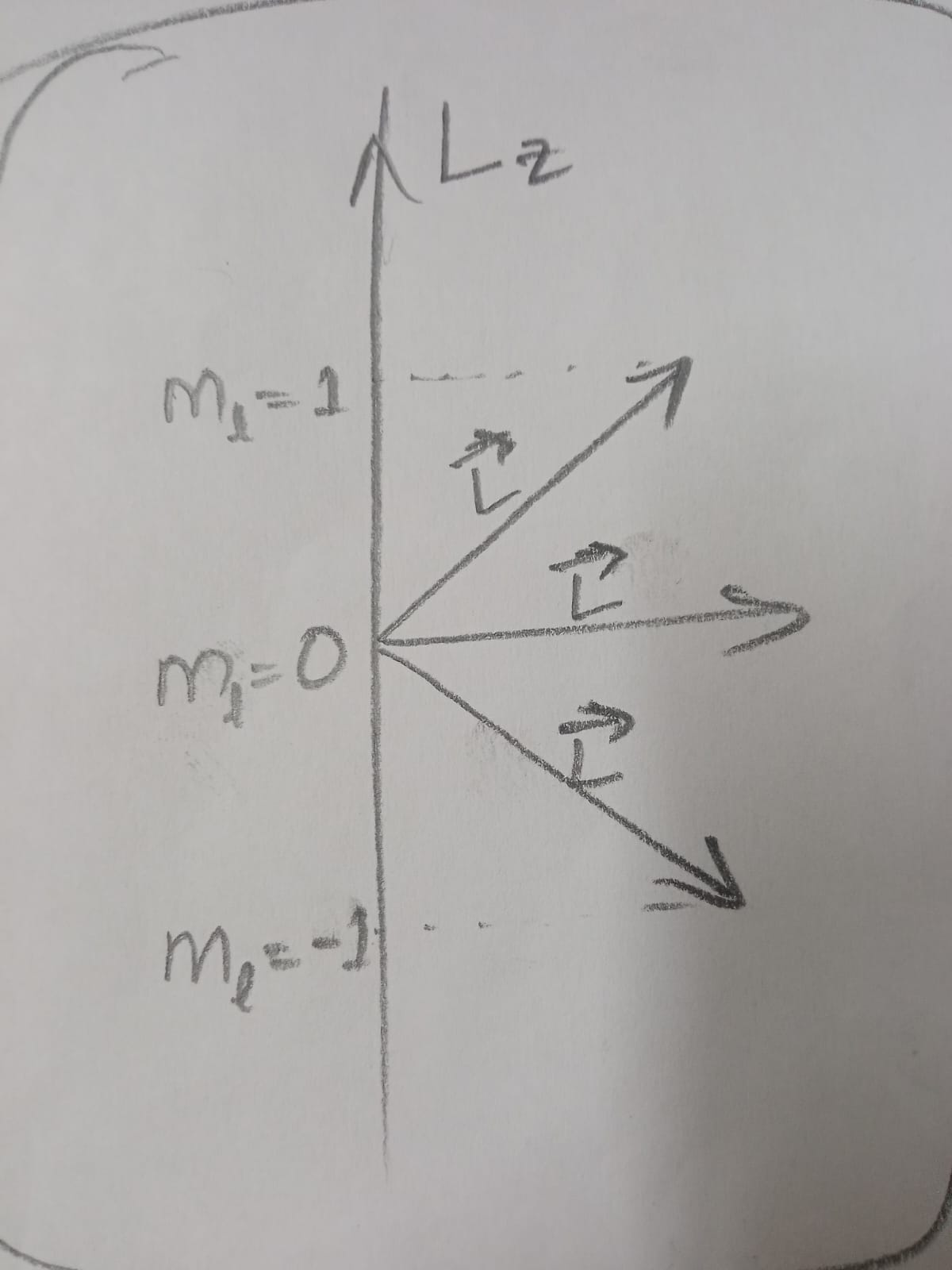
\(cos (\theta)= \frac{\hbar m_l}{\hbar \sqrt{l(l+1)}}\)
\(\theta\) is minimum for \(m_l=+1\)
\(cos (\theta)= \frac{1}{\sqrt{2}} \hspace{3mm} \theta=45^\circ\)
Q.No: 35
An electric field as a function of radial coordinate \(r\) has the form
\(\vec{E}=\alpha \frac{e^{-r^2}}{r}\hat{r}\) where \(\alpha\) is a constant. Assume that dimensions are appropriately taken care of. The electric flux through a sphere of radius \(\sqrt{2}\), centered at the origin, is \(\Phi\). What is the value of \(\frac{\Phi}{2\pi \alpha}\) (rounded off to two decimal places)?
Solution :
\[\Phi= \oint \vec{E} \cdot d\vec{a}\]
(Integral over spherical surface of radius \(r=\sqrt{2}\))
\(\Phi = \oint (\alpha \frac{e^{-r^2}}{r} \hat{r})\cdot (r^2 sin \hspace{0.3mm}\theta \hspace{0.3mm} d\theta \hspace{0.3mm} d\phi \hspace{0.3mm} \hat{r})\)
\(\Phi= \alpha \frac{e^{-2}}{\sqrt{2}}\times 2 \hspace{0.3mm} \oint \hspace{0.3mm} sin\hspace{0.3mm}\theta d\theta \hspace{0.3mm} d\phi\)
\(\Phi= \alpha \hspace{0.3mm} \sqrt{2} \hspace{0.3mm} e^{-2} \times 4\pi\)
\(\frac{\Phi}{2\pi \alpha}= \frac{\alpha \sqrt{2} e^{-2}\times 4\pi}{2\pi \hspace{0.3mm} \alpha}= 0.38\)
Q.No: 59
Two independent electrostatic configurations are shown in the figure.
Configuration (\(I\)) consists of an isolated point charge \(q = 1 \hspace{0.5mm} C\), and configuration (\(II\)) consists of another identical charge surrounded by a thick conducting shell of inner radius \(R_1=1 \hspace{0.5mm}m\) and outer radius \(R_2=2\hspace{0.5mm} m\), with the charge being at the center of the shell. \(W_I=\frac{\epsilon_0}{2}\int E_I ^2 dV\) and \(W_{II}=\frac{\epsilon_0}{2}\int E_{II} ^2 dV\) ,
where \(E_I\) and \(E_{II}\) are the magnitudes of the electric fields for configurations (\(I\)) and (\(II\)) respectively, \(\epsilon_0\) is the permittivity of vacuum, and the volume integration's are carried out over all space. If \(\frac{8\pi}{\epsilon_0}|W_I -W_{II}|=\frac{1}{n}\), what is the value of the integer \(n\)?

Solution :
\[E_I= \frac{1}{4\pi \epsilon_0} \frac{q}{r^2} \hspace{5mm} 0<r<\infty\]
\[E_{II}=\left\{
\begin{array}{lll}
\frac{1}{4\pi \epsilon_0} \frac{q}{r^2}, & 0<r<R_1 \\
0 ,& R_1<r<R_2 \\ \frac{1}{4\pi \epsilon_0} \frac{q}{r^2}, & R_2<r<\infty
\end{array}
\right.\]
\[W_I -W_{II}=\frac{\epsilon_0}{2} \int E_I ^2 dV -\frac{\epsilon_0}{2}\int E_{II}^2 dV\]
\(dV= r^2 dr \hspace{0.5mm} sin \hspace{0.5mm} \theta \hspace{0.5mm} d\theta \hspace{0.5mm} d\phi\)
\(\iint sin \theta \hspace{0.5mm} d\theta \hspace{0.5mm} d\phi =4\pi\)
\[W_I -W_{II} =\frac{\epsilon_0 }{2} \frac{q^2}{(4\pi \epsilon_0)^2}[\int_0 ^\infty \frac{1}{r^4} r^2 dr \times 4 \pi \\ - \int_0 ^{R_1} \frac{1}{r^4} r^2 dr \times 4\pi -\int_{R_2} ^{\infty} \frac{1}{r^4} r^2 dr \times 4\pi]\]
\[W_I -W_{II}=\frac{q^2}{2 \times(4\pi)^2 \epsilon_0}4\pi [\int_0 ^{R_1}\frac{1}{r^2} dr +\int_{R_1} ^{\infty}\frac{1}{r^2} dr - \int_0 ^{R_1}\frac{1}{r^2} dr-\int_{R_2} ^{\infty}\frac{1}{r^2} dr ] \]
\[W_I -W_{II}= \frac{q^2}{8\pi \epsilon_0}\left[\int_{R_1} ^{\infty}\frac{1}{r^2} dr-\int_{R_2} ^{\infty}\frac{1}{r^2} dr\right]\]
\[=\frac{q^2}{8\pi \epsilon_0} \{\left[-\frac{1}{r} \right]_{R_1} ^\infty -\left[-\frac{1}{r}\right]_{R_2} ^\infty\}\]
\[W_I -W_{II}=\frac{q^2}{8\pi \epsilon_0} (\frac{1}{R_1}-\frac{1}{R_2}) \]
Given \(q=1C, \hspace{2mm} R_1=1m, \hspace{2mm} R_2=2m\)
\[\Rightarrow 8\pi \epsilon_0 |W_I -W_{II}|=\frac{1}{2}\]
\[\Rightarrow n=2\]
(In the question, they have given \(\frac{8 \pi}{\epsilon_0} |W_I -W_{II}| \), but it should be \( 8 \pi \epsilon_0 |W_I -W_{II}| \) )
Q.No: 60
In pion nucleon scattering, the pion and nucleon can combine to form a short lived bound state called the \(\Delta\) particle (\(\pi +n \to \Delta\)). The masses of the pion, nucleon and the \(\Delta\) particle are 140 MeV/\(c^2\), 938 MeV/\(c^2\) and 1230 MeV/\(c^2\), respectively. In the lab frame, where the nucleon is at rest, what is the minimum
energy (in MeV/\(c^2\), rounded off to one decimal place) of the pion to produce the \(\Delta\) particle?
Solution :
Consider,
\[A+B \to C+D\]
Threshold KE is given by
\[(T_A)_{Th}=\frac{- Q \times (m_A+m_B+m_C+m_D)}{2m_B}\]
Where, \(Q=(m_A + m_B -m_C - m_D) c^2\)
In this question,
\[\pi + N \to \Delta\]
Using give data, threshold KE of pion is
\((T_{\pi})_{Th}=187MeV\)
Total threshold energy of pion (minimum energy required )
\[
E_{\pi}=(T_{\pi})_{Th} + m_{\pi}c^2 = 327 MeV
\]
Q.No: 61
Consider an electromagnetic wave propagating in the z-direction in vacuum, with the magnetic field given by \(\vec{B} = \vec{B}_0 e^{i(kz-\omega t)}\). If \(\vec{B}_0=10^{-8} T\), the average power passing through a circle of radius 1.0 m placed in the xy plane is \(P\) (in
Watts). Using \(\epsilon_0 =10^{-11} \frac{c^2}{N \hspace{0.5mm}m^2 }\), what is the value of \(\frac{10^3 P}{\pi}\) (rounded off to one decimal place) ?
Solution :
Wave travelling along z-axis, i.e. perpendicular to x-y plane.
Time average of poynting vector is
\[\langle \vec{S}\rangle =\frac{1}{2} c \hspace{0.5mm} \epsilon_0 \hspace{0.5mm} E_0 ^2 \hat{z} \]
\(B_0=\frac{E_0}{2} , \hspace{3mm} E_0 = B_0 c\)
\(\langle \vec{S}\rangle =\frac{1}{2} \epsilon_0 \hspace{0.5mm} c \times B_0 ^2 \hspace{0.5mm} c^2 \hat{z}\)
\(\langle \vec{S}\rangle=\frac{1}{2} \epsilon_0 B_0^2 c^3 \hat{z}\)
Poynting vector is power per unit area. So, power passing through circle of radius \(r=1m\) is
\[P=|\langle \vec{S}\rangle|\times \pi r^2=\frac{1}{2} \epsilon_0 B_0 ^2 c^3 \times \pi \cdot 1^2\]
\(\frac{10^3 P}{\pi}=\frac{10^3}{\pi}\times \frac{1}{2} \epsilon_0 B_0 ^2 c^3 \times \pi\)
\(\frac{10^3 P}{\pi} =13.6\) watt.
Q.No: 62
An \(\alpha\)-particle is emitted from the decay of Americium (\(Am\)) at rest, i.e., \(^{241} _{94} Am \to ^{237} _{92} U +\alpha\). The rest masses of \(^{241} _{94} Am ,^{237} _{92} U \) and \(\alpha\) are 224.544
GeV/\(c^2\), 220.811 GeV/\(c^2\) and 3.728 GeV/\(c^2\) respectively. What is the kinetic energy (in MeV/\(c^2\), rounded off to two decimal places) of the \(\alpha\)-particle?
Solution :
\(A\to B+C\)
\[T_B=\frac{(m_A-m_B-m_C)(m_A-m_B +m_C)c^2}{2m_A}\]
\[T_C=\frac{(m_A-m_B-m_C)(m_A-m_C +m_B)c^2}{2m_A}\]
\(A_m \to U+\alpha\)
\[\Rightarrow T_\alpha =\frac{(m_{A_m} -m_U-m_\alpha )(m_{A_m} -m_\alpha+m_U )c^2}{2 m_{A_m}}\]
\(=0.004196\) GeV
\(=4.92\) MeV
\(=4.92\) MeV
Q.No: 63
Consider 6 identical, non-interacting, spin \(\frac{1}{2}\) atoms arranged on a crystal lattice at absolute temperature \(T\). The z-component of the magnetic moment of each of these atoms can be \(\pm \mu_B\). If \(P\) and \(Q\) are the probabilities of the net magnetic
moment of the solid being \(2\mu_B\) and \(6\mu_B\) respectively, what is the value of \(\frac{P}{Q}\) (in integer)?
Solution :
Each atom can be in two state with respective magnetic momentum \(+\mu_B\) and \(-\mu_B\).
Total number of possible arrangements of 6 such atoms is
\(\Omega = (2)^6\) (Principle of counting)
We get total magnetic momentum \(2\mu_B\) when 4 atoms are spin up and 2 atoms are spin down. Number of possible ways for this is \(\frac{6!}{2! 4!}=15\)
So, \(P=\frac{15}{2^6}\)
We will get total magnetic momentum \(6\mu_B\) when all 6 atoms are spin up and no atoms are spin down.
Number of permutations for this is 1.
So, \(Q=\frac{1}{2^6}\)
\(\frac{P}{Q}=15\)
(*** Temperature should not be mentioned. If system is in thermal equilibrium, then probability is governed by Canonical Distribution.
Also, it would have been nice if they have mentioned weather to take particles distinguishable or indistinguishable.)
Q.No: 64
Two identical, non-interacting \(^4 He _2\) atoms are distributed among 4 different nondegenerate energy levels. The probability that they occupy different energy levels is \(p\). Similarly, two \(^3 He_2\) atoms are distributed among 4 different non-degenerate energy levels, and the probability that they occupy different levels is \(q\). What is
the value of \(\frac{p}{q}\) (rounded off to one decimal place)?
Solution :
Let us take \(^4 He_2\). It is a boson.
Total number of ways of distributing \(n\) bosons in \(g\) number of levels
\(\Omega=\frac{(n+g-1)!}{n!(g-1)!}\)
In this case, \(n=2\) and \(g=4\)
\[\Omega=\frac{(2+4-1)!}{2!(4-1)!}=\frac{5!}{2! 3!}=10\]
Number of ways of distributing two bosons so that all are in different energy levels is 6.
So, \(p=\frac{6}{10}=0.6\)

Now, let us take \(^3He_2\). It is a fermion.
Total number of ways of distributing \(n\) fermions in \(g\) levels is \(\Omega= ^g C_n \)
Since fermions do not occupy the same energy level, number of ways they occupy different level is also \(\Omega= ^g C_n \) only.
So \(q=1\).
\(\frac{p}{q}=\frac{0.6}{1}=0.6\)
Q.No: 65
Two identical bodies kept at temperatures 800 K and 200 K act as the hot and the cold reservoirs of an ideal heat engine, respectively. Assume that their heat capacity (\(C\)) in Joules/K is independent of temperature and that they do not undergo any phase change. Then, the maximum work that can be obtained from the heat engine is \(n \times C\) Joules. What is the value of \(n\) (in integer)?
Solution :
Suppose \(T_H\) and \(T_C\) are the temperatures of hot and cold reservoirs respectively. Let \(T_f\) be the final temperature attainable by both reservoirs, then
Heat received from hot reservoir : \(|Q_H|=C (T_H-T_f)\)
Heat taken by cold reservoir : \(|Q_C|=C (T_f-T_C)\)
Work done by the engine : \(W=|Q_H|-|Q_C|\)
\[W=C(T_H+T_C -2T_f)\]
The most efficient engine is reversible one for which \(\Delta S=0\)
\[\Delta S=\int dS =\int \frac{dQ}{T} =\int_{T_H} ^{T_f} \frac{C \hspace{0.3mm} dT}{T} +\int_{T_C} ^{T_f} \frac{C \hspace{0.3mm} dT}{T}=0 \]
\[C\hspace{0.5mm} ln \left(\frac{T_f}{T_H} \right) +C\hspace{0.5mm} ln\left(\frac{T_f}{T_C}\right)=0 \]
\[ln \left(\frac{T_f ^2}{T_H T_C} \right)=0\]
So, \(T_f ^2= T_H T_C \) for the most efficient engine.
\[T_f=\sqrt{T_H T_C}\]
\[W_{max}=C \times (T_H+T_C-2 \sqrt{T_H T_C}) =n\times C \]
\(T_H=800 K \), \(T_C=200 K \)
So, \(n=200\)
Multiple Select Questions
Q.No: 11
Which one of the following entropy (S) - temperature (T) diagrams CORRECTLY represents the Carnot cycle \(abcda\) shown in the P-V diagram?
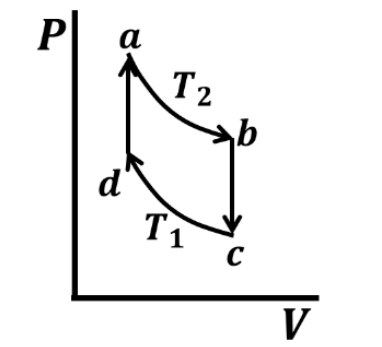

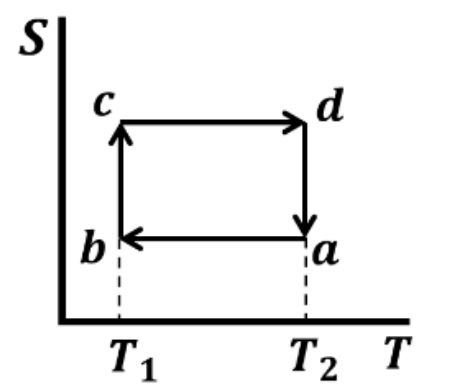

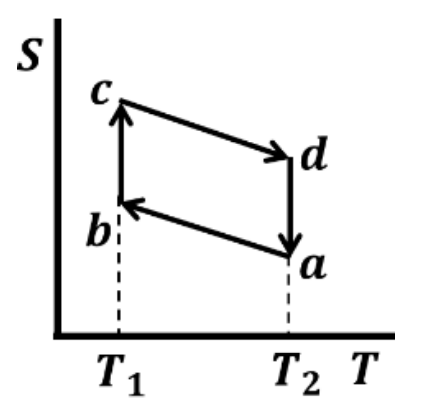
Solution :
\(a \to b\) and \(c \to d\) are iso-thermal processes that occurs at constant temperature(\(T_2\) and \(T_1\) respectively). During this process, heat exchange occurs and entropy changes.
\(b \to c\) and \(d \to a\) are adiabatic processes that involve no heat exchange \((dQ=TdS=0)\) and hence no change in entropy.
Option A is the right one.
Q.No: 12
Which one of the following is a dimensionless constant?
(A) Permittivity of free space
(B) Permeability of free space
(C) Bohr magneton
(D) Fine structure constant
Solution :
Fine structure constant is a ratio of velocity of electron in first Bohr orbit of H-atom to velocity of light.
\[\alpha=\frac{v}{c}\]
It is dimensionless.
Q.No: 13
Choose the most appropriate matching of the items in Column 1 with those in Column 2.
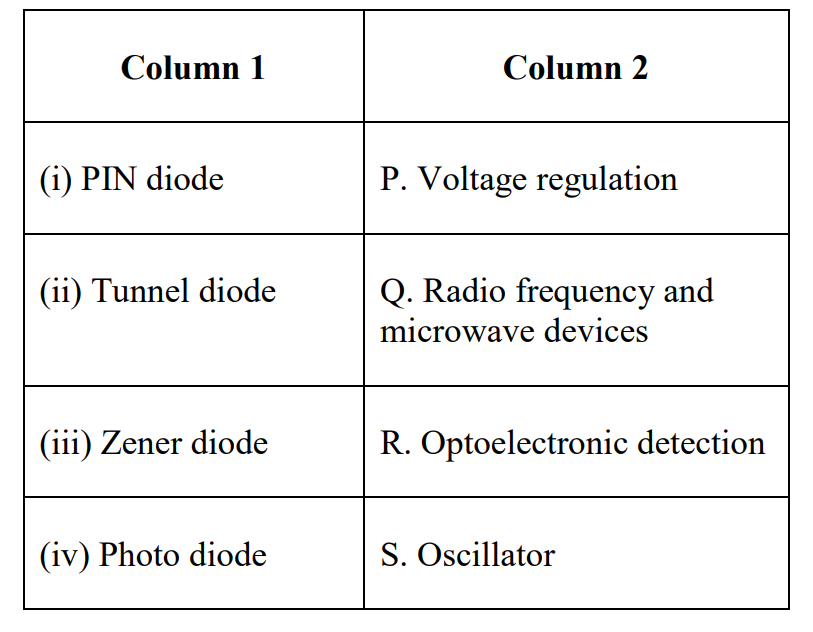
(A) (i) - Q; (ii) - S; (iii) - P; (iv) - R
(B) (i) - R; (ii) - Q; (iii) - P; (iv) - S
(C) (i) - R; (ii) - S; (iii) - P; (iv) - Q
(D) (i) - P; (ii) - Q; (iii) - R; (iv) - S
Solution :
Zenor diode used for voltage regulation.
Tunnel diode used to design oscillators.
Photo diode obviously used for optoelectronic detection.
PIN diode is multipurpose.
Option A is the appropriate one.
Q.No: 14
The atomic number of an atom is 6. What is the spectroscopic notation of its ground state, according to Hund’s rules?
(A) \(^3 P_0\)
(B) \(^3 P_1\)
(C) \(^3 D_3\)
(D) \(^3 S_1\)
Solution :
Electronic configuration : \(1s^2 \hspace{1mm} 2s^2 \hspace{1mm} 2p^2\)
i.e., we have two equivalent unpaired electrons in p-orbit.
\(l_1=1, \hspace{1mm} l_2=1, \hspace{1mm} L=0,1,2\)
\(s_1=\frac{1}{2}, \hspace{1mm} s_2=\frac{1}{2}, \hspace{1mm} S=0,1\)
Spacial state is symmetric for \(L=0 \) and \(2\) and it is anti-symmetric for \(L=1\)
Spin state is symmetric for \(S=1\) and is anti-symmetric for \(S=0\)
To make total state anti-symmetric (system of fermions), we need to combine \(S=0\) with \(L=0,2\) and \(S=1\) with \(L=1\).
According to Hund's rule, states corresponds to higher \(S\) value lies below.
\(S=1 , L=1 , J=0,1,2\), (i.e. \(^3P_0 ,^3P_1 , ^3P_2 \) ) states lies below the \(S=0\) states.
Since it is less than half filled (\(p^2\)), according to Hund's rule, among \(^3P_0 ,^3P_1 , ^3P_2 \), lower \(J\) value state lies below.
So, the ground state is \(^3P_0\)
Q.No: 19
For a non-magnetic metal, which one of the following graphs best represents the behaviour of \(\frac{C}{T}\) vs. \(T^2\), where \(C\) is the heat capacity and \(T\) is the temperature?


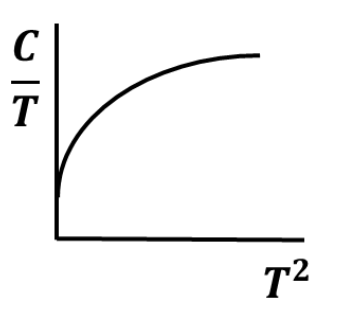

Solution :
For metals \(C=AT+BT^3\)
\(A \hspace{0.5mm} T\) is electronic contribution and \(BT^3\) is lattice contribution (Phononic).
\[\frac{C}{T}=A+BT^2\]
\(\frac{C}{T}\) v/s \(T^2\) is a straight line with slope \(B\) and y-intercept \(A\)
Option B is the right one.
Q.No: 20
For nonrelativistic electrons in a solid, different energy dispersion relations (with effective masses \(m_a ^*, m_b ^*\) and \(m_c ^*\)) are schematically shown in the plots. Which one of the following options is CORRECT?

(A) \(m_a ^*=m_b ^*=m_c ^*\)
(B) \(m_b ^*>m_c ^*>m_a ^*\)
(C) \(m_c ^*>m_b ^*>m_a ^*\)
(D) \(m_a ^*>m_b ^*>m_c ^*\)
Solution :
Effective mass \(m^*\) is given by
\[m^*=\frac{\hbar^2}{(\frac{d^2 E}{dk^2})}\]
where \(\frac{d^2 E}{dk^2}\) should be taken at the extremum. (i.e., at \(k=0\) in this case)
Second derivative tells us how fast first derivative (slope of the tangent) changes.
For the curve with more curvature, slope of the tangent / first derivative changes faster and hence second derivative is more. For the curve with less curvature, slope of the tangent / first derivative changes slowly and hence second derivative is relatively less.
Curve-c have got more curvature and hence more \(\frac{d^2 E}{dk^2}\) and hence less \(m_c ^*\)
Curve-a have got less curvature and hence \(\frac{d^2 E}{dk^2}\) is relatively less and hence \(m_a ^*\) is more.
Curve-b is intermediate between curve-a and curve-c
So, \(m_a^* > m_b^*> m_c ^*\)
