Q.No:1 JEST-2012
If the coordinate \(q\) and the momentum \(p\) form a canonical pair \((q, p)\), which one of the sets given below also forms a canonical pair?
(a)
\((q, -p)\)
(b)
\((q^2, p^2)\)
(c)
\((p, -q)\)
(d)
\((q^2, -p^2)\)
Check Answer
Option c
Q.No:2 JEST-2013
If the Poisson bracket \(\{x, p\}=-1\), then the Poisson bracket \(\{x^2+p, p\}\) is
(a)
\(-2x\)
(b)
\(2x\)
(c)
\(1\)
(d)
\(-1\)
Check Answer
Option a
Q.No:3 JEST-2014
A dynamical system with two generalized coordinates \(q_1\) and \(q_2\) has Lagrangian \(L=\dot{q}_1^2+\dot{q}_2^2\). If \(p_1\) and \(p_2\) are the corresponding generalized momenta, the Hamiltonian is given by
(a)
\((p_1^2+p_2^2)/4\)
(b)
\((\dot{q}_1^2+\dot{q}_2^2)/4\)
(c)
\((p_1^2+p_2^2)/2\)
(d)
\((p_1\dot{q}_1+p_2\dot{q}_2)/4\)
Check Answer
Option a
Q.No:4 JEST-2017
\((Q_1, Q_2, P_1, P_2)\) and \((q_1, q_2, p_1, p_2)\) are two sets of canonical coordinates, where \(Q_i\) and \(q_i\) are the coordinates and \(P_i\) and \(p_i\) are the corresponding conjugate momenta. If \(P_1=q_2\) and \(P_2=p_1\), then which of the following relations is true?
(A)
\(Q_1=q_1, Q_2=p_2\)
(B)
\(Q_1=p_2, Q_2=q_1\)
(C)
\(Q_1=-p_2, Q_2=q_1\)
(D)
\(Q_1=q_1, Q_2=-p_2\)
Check Answer
Option C
Q.No:5 JEST-2018
If \((q, p)\) is a canonically conjugate pair, which of the following is not a canonically conjugate pair?
(A)
\((q^2, pq^{-1}/2)\)
(B)
\((p^2, -qp^{-1}/2)\)
(C)
\((pq^{-1}, -q^2)\)
(D)
\((f(p), -q/f'(p))\), where \(f'(p)\) is the derivative of \(f(p)\) with respect to \(p\).
Check Answer
Option C
Q.No:6 JEST-2018
The coordinate \(q\) and the momentum \(p\) of a particle satisfy
\[
\frac{dq}{dt}=p, \frac{dp}{dt}=-3q-4p.
\]
If \(A(t)\) is the area of any region of points moving in the \((q,p)\)-space, then the ratio \(A(t)/A(0)\) is
(A)
\(1\)
(B)
\(\exp{(-3t)}\)
(C)
\(\exp{(-4t)}\)
(D)
\(\exp{(-3t/4)}\)
Check Answer
Option C
Q.No:7 JEST-2019
Consider the following transformation of the phase space coordinates \((q, p)\to (Q, P)\).
\[
Q=q^a \cos{bp} ~ P=q^a \sin{bp}
\]
For what values of \(a\) and \(b\) will the transformation be canonical?
(A)
\(1, 1\)
(B)
\(1/2, 1/2\)
(C)
\(2, 1/2\)
(D)
\(1/2, 2\)
Check Answer
Option D
Q.No:8 JEST-2020
A particle of mass \(m\) moves in a one-dimensional potential \(V(x)=F_0|x|\), where \(F_0\) is a positive constant. Given the initial conditions, \(x(0)=x_0>0\) and \(\dot{x}(0)=0\), which one of the following statements is correct?
(A)
The particle undergoes simple harmonic motion about the origin with frequency \(\omega=2\pi\sqrt{F_0/mx_0}\)
(B)
The angular frequency of oscillations of the particle is \(\omega=\frac{1}{2}\pi\sqrt{F_0/2mx_0}\)
(C)
The particle begins from rest and is accelerated along the positive \(x\) axis such that \(x(t)=x_0+F_0 t^2/2m\)
(D)
The angular frequency of oscillations of the particle is independent of its mass
Check Answer
Option B
Q.No:9 JEST-2020
The Hamiltonian for a particle of mass \(m\) is given by \(H=(p-\alpha q)^2/(2m)\), where \(\alpha\) is a non-zero constant. Which one of the following equations is correct?
(A)
\(p=m\dot{q}\)
(B)
\(\alpha \dot{p}=\dot{q}\)
(C)
\(\ddot{q}=0\)
(D)
\(L=\frac{1}{2}m\dot{q}^2-\alpha q\dot{q}\)
Check Answer
Option C
Q.No:10 JEST-2020
The Hamiltonian of a classical particle is given by \(\mathcal{H}(p, q)=p^2/2m+kq^2/2\). Given \(F(p, q, t)=\ln{(p+im\omega q)}-i\alpha \omega t\) is a constant of motion (where \(\omega=\sqrt{k/m}\)), what is the value of \(\alpha\)?
(A)
\(2\pi\)
(B)
\(0\)
(C)
\(1\)
(D)
\(\pi\)
Check Answer
Option C
Q.No:11 JEST-2020
Consider a particle with total energy \(E\) is oscillating in a potential \(U(x)=A|x|^n\) with \(A>0\) and \(n>0\) in one dimension. Which one of the following gives the relation between the time-period of oscillation \(T\) and the total energy \(E\):
(A)
\(T\propto E^{1/n-1/2}\)
(B)
\(T\propto E^{0}\)
(C)
\(T\propto E^{n}\)
(D)
\(T\propto E^{1/n}\)
Check Answer
Option A
Q.No:12 JEST-2021
Which one of the following sets correctly represents the Hamilton's equations of motion obtained from the Lagrangian \(L=\frac{1}{2}m\dot{x}\dot{y}-\frac{1}{2}m\omega^2 xy\)?
(A)
\(m\dot{x}=2p_y, \dot{p}_x=-\frac{1}{2}m\omega^2 y, m\dot{y}=2p_x, \dot{p}_y=-\frac{1}{2}m\omega^2 x\)
(B)
\(m\dot{x}=2p_y, \dot{p}_x=-\frac{1}{2}m\omega^2 x, m\dot{y}=2p_x, \dot{p}_y=-\frac{1}{2}m\omega^2 y\)
(C)
\(m\dot{x}=p_x, \dot{p}_x=-m\omega^2 x, m\dot{y}=p_y, \dot{p}_y=-m\omega^2 y\)
(D)
\(m\dot{x}=p_y, \dot{p}_x=-m\omega^2 y, m\dot{y}=p_x, \dot{p}_y=-m\omega^2 x\)
Check Answer
Option A
Q.No:13 JEST-2022
The Lagrangian of a particle of unit mass is given by \(L=\frac{1}{2}(\dot{x}^2-x^2+2x\dot{x})\). The Hamiltonian of this system is given by
(a)
\(\frac{1}{2}p^2-px+x^2\)
(b)
\(\frac{1}{2}(p^2+x^2)\)
(c)
\(\frac{1}{2}(p-x)^2\)
(d)
\(\frac{1}{2}p^2+px-x^2\)
Check Answer
Option a
Q.No:14 JEST-2024
Let \( q \) and \( p \) be the canonical phase space coordinates of a system, where \( q \) is the generalized coordinate and \( p \) is the generalized momentum. Let us make a transformation of the generalized coordinate as \( Q = q^2 \). Which of the following functions is canonically conjugate to \( Q \)?
A) \( \frac{p}{2q} \)
B) \( \frac{p}{q} \)
C) \( p^2 \)
D) \( \frac{p^2}{2q^2} \)
Check Answer
Option a
Q.No:1 TIFR-2012
A dynamical system with two degrees of freedom, has generalised coordinates \(q_1\) and \(q_2\), and kinetic energy
\[
T=\lambda \dot{q}_1 \dot{q}_2
\]
If the potential energy is \(V(q_1, q_2)=0\), the correct form of the Hamiltonian for this system is
(a)
\(p_1 p_2/\lambda\)
(b)
\(\lambda \dot{q}_1 \dot{q}_2\)
(c)
\((p_1 \dot{q}_1+p_2 \dot{q}_2)/2\)
(d)
\((p_1 q_2+p_2 q_1)/2\)
Check Answer
Option a
Q.No:2 TIFR-2013
If a central force acting on a particle of mass \(m\) is given by
\[
F(r)=-\frac{k}{r^2}
\]
where \(r\) is the distance of the particle from the origin and \(k\) is a positive constant, the Hamiltonian for the system, in spherical polar coordinates, will have the form
(a)
\(\frac{1}{2}m(\dot{r}^2+r^2\dot{\theta}^2+r^2\sin^2{\theta}\dot{\varphi}^2)+\frac{k}{r}\)
(b)
\(\frac{p_r^2}{2m}+\frac{p_{\theta}^2}{2mr^2}+\frac{p_{\varphi}^2\csc^2{\theta}}{2mr^2}+\frac{k}{r}\)
(c)
\(\frac{1}{2mr^2}(r^2 p_r^2+p_{\theta}^2+p_{\varphi}^2+2mkr)\)
(d)
\(\frac{p_r^2}{2m}+\frac{p_{\theta}^2}{2m}+\frac{p_{\varphi}^2}{2m}+\frac{k}{r}\)
Check Answer
Option b
Q.No:3 TIFR-2015
In a system with two degrees of freedom, if \((p, q)\) are the canonical coordinates, then which of the following transformations to \((P, Q)\) is canonical?
(a)
\(P=\frac{1}{2}(p^2+q^2), Q=\tan^{-1}{\frac{2q}{p}}\)
(b)
\(P=\frac{1}{2}(p^2+q^2), Q=\cot^{-1}{\frac{p}{q}}\)
(c)
\(P=\frac{1}{2}(p^2+q^2), Q=\sin^{-1}{\frac{q}{2p}}\)
(d)
\(P=\frac{1}{2}(p^2+q^2), Q=\cos^{-1}{\frac{p}{q}}\)
Check Answer
Option b
Q.No:4 TIFR-2017
The Lagrangian of a system described by a single generalised coordinate \(q\) is
\[
L=\frac{1}{2}\dot{q}\sin^2{q}
\]
Its Hamiltonian is
(a)
not defined
(b)
Zero
(c)
\(-\dot{q}\sin^2{q}\)
(d)
\(\dot{q}\left(p-\frac{1}{2}\sin^2{q}\right)\)
Check Answer
Option a
Q.No:5 TIFR-2018
The Hamiltonian of a dynamical system is equal to its total energy, provided that its Lagrangian
(a)
does not contain velocity-dependent terms.
(b)
is separable in generalized coordinates and velocities.
(c)
does not have terms which explicitly depend on the coordinates.
(d)
has no explicit time dependence.
Check Answer
Option d
Q.No:6 TIFR-2018
A dynamical system with one degree of freedom is described by canonical coordinates \((p, q)\). The generator \(F\) of the canonical transformation \((p, q)\to (-q, p)\) is
(a)
\(F=-p\dot{q}\)
(b)
\(F=p\dot{q}\)
(c)
\(F=-\dot{p}q\)
(d)
\(F=pq\)
Check Answer
Option d
Q.No:7 TIFR-2019
A bead of mass \(m\) slides under the influence of gravity along the frictionless interior of a hemispherical cup of radius \(a\) sunk vertically into the ground with its open side level with the ground (see sketch on the right). In terms of spherical polar coordinates \((\theta, \varphi)\) set up with the centre of the upper circle as origin, the Hamiltonian \(H\) for this system will be
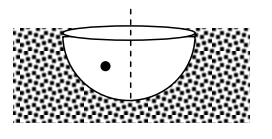
(a)
\(H=\frac{m}{2}(a^2\dot{\theta}^2+a^2\dot{\varphi}^2\csc^2{\theta})+2mga\sin^2{\frac{\theta}{2}}\)
(b)
\(H=\frac{m}{2}(a^2\dot{\theta}^2+a^2\dot{\varphi}^2\sin^2{\theta})+2mga\sin^2{\frac{\theta}{2}}\)
(c)
\(H=\frac{1}{2ma^2}(p_{\theta}^2+p_{\varphi}^2\sin^2{\theta})+2mga\sin^2{\frac{\theta}{2}}\)
(d)
\(H=\frac{1}{2ma^2}(p_{\theta}^2+p_{\varphi}^2\csc^2{\theta})+2mga\sin^2{\frac{\theta}{2}}\)
Check Answer
Option d
Q.No:8 TIFR-2020
The Lagrangian of a system described by generalised coordinates \(q_1\) and \(q_2\) is given by
\[
L=\frac{a}{2}(\dot{q}_1^2+\dot{q}_2^2)-\frac{b^2}{\pi}(q_1^2+q_2^2)
\]
where \(a\) and \(b\) are constants. It follows that a conserved quantity in this system is
(a)
\(q_1\dot{q}_2-q_2 \dot{q}_1\)
(b)
\(q_1\dot{q}_2+q_2 \dot{q}_1\)
(c)
\(\frac{q_1\dot{q}_2-q_2 \dot{q}_1}{q_1^2+q_2^2}\)
(d)
\(2\pi(q_1^2\dot{q}_2+q_2^2 \dot{q}_1\)
Check Answer
Option a
Q.No:9 TIFR-2021
A particle of mass \(m\), moving in one dimension \(x\) satisfies the Lagrangian
\[
L=\frac{1}{2}m\dot{x}^2 e^{2kx}
\]
where \(k\) is a constant.
If \(H\) is the Hamiltonian of the system, the canonical equations of motion are
(a)
\(\dot{x}=\frac{p}{m}e^{-2kx}, \dot{p}=-2kH\)
(b)
\(\dot{x}=\frac{p}{m}e^{2kx}, \dot{p}=-2H\)
(c)
\(\dot{x}=\frac{p}{m}e^{-2kx}, \dot{p}=-\frac{1}{2}kH\)
(d)
\(\dot{x}=\frac{p}{m}e^{-2kx}, \dot{p}=-2H\)
Check Answer
Option a
Q.No:10 TIFR-2023
Consider the Hamiltonian for a one-dimensional classical oscillator
\[H=\frac{1}{2m} (p^2+m^2\omega^2 q^2)\]
A Canonical transformation to variables \((P,Q)\) via the generating function
\[F=\frac{m \omega q^2}{2} cot \hspace{1mm} Q\] leads to which of the following Hamiltonian in the new coordinates?
(a)
\(H=P^2+\omega^2 Q^2\)
(b)
\(H=2\omega Q\)
(c)
\(H=\omega P\)
(d)
\(H=2\omega P\)
Check Answer
Option c
Q.No:11 TIFR-2024
A particle of mass \( m \) is attached to a massless string of length \( L \). The other end of the string is fixed at a point \( P \) as shown in the figure. \( m \) moves under gravity and the tension of the string. The motion of the string is described using the generalized coordinates \( \theta \) and \( \phi \) which change with time. \( \theta \) is the polar angle made by the string with the vertical and \( \phi \) is the azimuthal angle made by the projection of the string on the \( xy \) plane. The conjugate momenta to the variables \( (\theta, \phi) \) are \( (p_\theta, p_\phi) \), respectively.
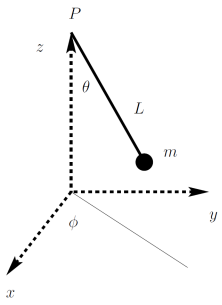
Assuming that the string is tight throughout the motion, the Hamiltonian for the system is given by:
(a) \( \frac{1}{2m} \left[ p_\theta^2 + p_\phi^2 cosec^2\theta \right] + 2mgL \sin^2\left(\frac{\theta}{2}\right) \)
(b) \( \frac{1}{2m} \left[ p_\theta^2 + p_\phi^2 cosec^2\theta \right] - 2mgL \sin^2\left(\frac{\theta}{2}\right) \)
(c) \( \frac{1}{2m} \left[ p_\theta^2 + p_\phi^2 \sin^2\theta \right] + 2mgL \sin^2\left(\frac{\theta}{2}\right) \)
(d) \( \frac{1}{2m} \left[ p_\theta^2 + p_\phi^2 \sin^2\theta \right] - 2mgL \sin^2\left(\frac{\theta}{2}\right) \)

Question 6