Hamiltonian Mechanics CSIR - S. N. Bose Physics Learning Center

Q.No:1 CSIR Dec-2014

The Hamiltonian of a classical particle moving in one dimension is \[ H=\frac{p^2}{2m}+\alpha q^4 \] where \(\alpha\) is a positive constant and \(p\) and \(q\) are its momentum and position respectively. Given that its total energy \(E\leq E_0\) the available volume of phase space depends on \(E_0\) as

(1) \(E_0^{3/4}\)

(2) \(E_0\)

(3) \(\sqrt{E_0}\)

(4) is independent of \(E_0\)

Check Answer

Option 1

Q.No:2 CSIR Dec-2014

The expression \[ \sum_{i, j, k=1}^{3} \epsilon_{ijk} \left\{x_i, \left\{p_j, L_k\right\}\right\} \] (where \(\epsilon_{ijk}\) is the Levi-Civita symbol, \(\vec{\mathbf{x}}, \vec{\mathbf{p}}, \vec{\mathbf{L}}\) are the position, momentum and angular momentum respectively, and \(\{A, B\}\) represents the Poisson bracket of \(A\) and \(B\)) simplifies to

(1) \(0\)

(2) \(6\)

(3) \(\vec{\mathbf{x}}.(\vec{\mathbf{p}}\times \vec{\mathbf{L}})\)

(4) \(\vec{\mathbf{x}}\times \vec{\mathbf{p}}\)

Check Answer

Option 2

Q.No:3 CSIR Dec-2014

A mechanical system is described by the Hamiltonian \(H(q, p)=\frac{p^2}{2m}+\frac{1}{2}m\omega^2 q^2\). As a result of the canonical transformation generated by \(F(q, Q)=-\frac{Q}{q}\), the Hamiltonian in the new coordinate \(Q\) and momentum \(P\) becomes

(1) \(\frac{1}{2m}Q^2 P^2+\frac{m\omega^2}{2}Q^2\)

(2) \(\frac{1}{2m}Q^2 P^2+\frac{m\omega^2}{2}P^2\)

(3) \(\frac{1}{2m}P^2+\frac{m\omega^2}{2}Q^2\)

(4) \(\frac{1}{2m}Q^2 P^4+\frac{m\omega^2}{2}P^{-2}\)

Check Answer

Option 4

Q.No:4 CSIR June-2015

If the Lagrangian of a dynamical system in two dimensions is \(L=\frac{1}{2}m\dot{x}^{2} + m\dot{x}\dot{y}\), then its Hamiltonian is

(1) \(H = \frac{1}{m}p_{x}p_{y} + \frac{1}{2m}p^{2}_y\)

(2) \(H = \frac{1}{m}p_{x}p_{y} + \frac{1}{2m}p^{2}_x\)

(3) \(H = \frac{1}{m}p_{x}p_{y} - \frac{1}{2m}p^{2}_y\)

(4) \(H = \frac{1}{m}p_{x}p_{y} + \frac{1}{2m}p^{2}_x\)

Check Answer

Option 3

Q.No:5 CSIR June-2015

Let \(q\) and \(p\) be the canonical coordinate and momentum of a dynamical system. Which of the following transformations is canonical?

A: \(Q_1 = \frac{1}{\sqrt{2}}q^{2}\) and \(P_{1} = \frac{1}{\sqrt{2}}p^{2}\)

B: \(Q_2 = \frac{1}{\sqrt{2}}(p + q)\) and\(P_{2} = \frac{1}{\sqrt{2}}(p - q)\)

(1) neither A nor B

(2) both A and B

(3) only A

(4) only B

Check Answer

Option 4

Q.No:6 CSIR June-2015

Which of the following figures is a schematic representation of the phase space trajectories (i.e., contours of constant energy) of a particle moving in a one-dimensional potential \\ \(V(x)\)=\(-\frac{1}{2}x^2+\frac{1}{4}x^4\)?

Check Answer

Option 1

Q.No:7 CSIR Dec-2015

A canonical transformation \((p, q)\to (P, Q)\) is performed on the Hamiltonian \(H=\frac{1}{2m}p^2+\frac{1}{2}m\omega^2 q^2\) via the generating function \(F=\frac{1}{2}m\omega q^2 \cot{Q}\). If \(Q(0)=0\), which of the following graphs shows schematically the dependence of \(Q(t)\) on \(t\)?

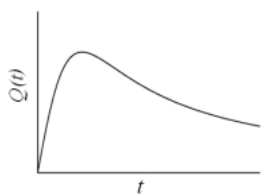
Check Answer

Option 4

Q.No:8 CSIR June-2016

The Hamiltonian of a system with generalized coordinate and momentum \((q, p)\) is \(H=p^2 q^2\). A solution of the Hamiltonian equation of motion is (in the following \(A\) and \(B\) are constants)

(1) \(p=Be^{-2At}, q=\frac{A}{B} e^{2At}\)

(2) \(p=Ae^{-2At}, q=\frac{A}{B} e^{-2At}\)

(3) \(p=Ae^{At}, q=\frac{A}{B} e^{-At}\)

(4) \(p=2Ae^{-A^2 t}, q=\frac{A}{B} e^{A^2 t}\)

Check Answer

Option 1

Q.No:9 CSIR June-2016

A canonical transformation \((q, p)\to (Q, P)\) is made through the generating function \(F(q, P)=q^2 P\) on the Hamiltonian \[ H(q, p)=\frac{p^2}{2\alpha q^2}+\frac{\beta}{4}q^4 \] where \(\alpha\) and \(\beta\) are constants. The equations of motion for \((Q, P)\) are

(1) \(\dot{Q}=P/\alpha\) and \(\dot{P}=-\beta Q\)

(2) \(\dot{Q}=4P/\alpha\) and \(\dot{P}=-\beta Q/2\)

(3) \(\dot{Q}=P/\alpha\) and \(\dot{P}=-\frac{2P^2}{Q}-\beta Q\)

(4) \(\dot{Q}=2P/\alpha\) and \(\dot{P}=-\beta Q\)

Check Answer

Option 2

Q.No:10 CSIR June-2016

The Lagrangian of a system moving in three dimensions is \[ L=\frac{1}{2}m\dot{x}_1^2+m(\dot{x}_2^2+\dot{x}_3^2)-\frac{1}{2}kx_1^2-\frac{1}{2}k(x_2+x_3)^2 \] The independent constant(s) of motion is/are

(1) energy alone

(2) only energy, one component of the linear momentum and one component of the angular momentum

(3) only energy and one component of the linear momentum

(4) only energy and one component of the angular momentum

Check Answer

Option 2

Q.No:11 CSIR Dec-2016

A particle in two dimensions is in a potential \(V(x, y)=x+2y\). Which of the following (apart from the total energy of the particle) is also a constant of motion?

(1) \(p_y-2p_x\)

(2) \(p_x-2p_y\)

(3) \(p_x+2p_y\)

(4) \(p_y+2p_x\)

Check Answer

Option 1

Q.No:12 CSIR June-2017

The Hamiltonian for a system described by the generalized coordinate \(x\) and generalised momentum \(p\) is \[ H=\alpha x^2 p+\frac{p^2}{2(1+2\beta x)}+\frac{1}{2}\omega^2 x^2 \] where \(\alpha, \beta\) and \(\omega\) are constants. The corresponding Lagrangian is

(1) \(\frac{1}{2}(\dot{x}-\alpha x^2)^2(1+2\beta x)-\frac{1}{2}\omega^2 x^2\)

(2) \(\frac{1}{2(1+2\beta x)}\dot{x}^2-\frac{1}{2}\omega^2 x^2-\alpha x^2\dot{x}\)

(3) \(\frac{1}{2}(\dot{x}^2-\alpha^2 x)^2(1+2\beta x)-\frac{1}{2}\omega^2 x^2\)

(4) \(\frac{1}{2(1+2\beta x)}\dot{x}^2-\frac{1}{2}\omega^2 x^2+\alpha x^2\dot{x}\)

Check Answer

Option 1

Q.No:13 CSIR June-2017

The energy of a one-dimensional system, governed by the Lagrangian \[ L=\frac{1}{2}m\dot{x}^2-\frac{1}{2}kx^{2n} \] where \(k\) and \(n\) are two positive constants, is \(E_0\). The time period of oscillation \(\tau\) satisfies

(1) \(\tau \propto k^{-\frac{1}{n}}\)

(2) \(\tau \propto k^{-\frac{1}{2n}} E_0^{\frac{1-n}{2n}}\)

(3) \(\tau \propto k^{-\frac{1}{2n}} E_0^{\frac{n-2}{2n}}\)

(4) \(\tau \propto k^{-\frac{1}{n}} E_0^{\frac{1+n}{2n}}\)

Check Answer

Option 2

Q.No:14 CSIR June-2017

A Hamiltonian system is described by the canonical coordinate \(q\) and canonical momentum \(p\). A new coordinate \(Q\) is defined as \(Q(t)=q(t+\tau)+p(t+\tau)\), where \(t\) is the time \(\tau\) is a constant, that is, the new coordinate is a combination of the old coordinate and momentum at a shifted time. The new canonical momentum \(P(t)\) can be expressed as

(1) \(p(t+\tau)-q(t+\tau)\)

(2) \(p(t+\tau)-q(t-\tau)\)

(3) \(\frac{1}{2}[p(t-\tau)-q(t+\tau)]\)

(4) \(\frac{1}{2}[p(t+\tau)-q(t+\tau)]\)

Check Answer

Option 4

Q.No:15 CSIR Dec-2017

A particle moves in one dimension in a potential \(V(x)=-k^2 x^4+\omega^2 x^2\) where \(k\) and \(\omega\) are constants. Which of the following curves best describes the trajectories of this system in phase space?

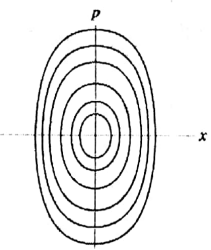
Check Answer

Option 2

Q.No:16 CSIR Dec-2017

Let \((x, p)\) be the generalized coordinate and momentum of a Hamiltonian system. If new variables \((X, P)\) are defined by \(X=x^{\alpha} \sinh{(\beta p)}\) and \(P=x^{\gamma} \cosh{(\beta p)}\), where \(\alpha, \beta\) and \(\gamma\) are constants, then the conditions for it to be a canonical transformation, are

(1) \(\alpha=\frac{1}{2\beta}(\beta+1)\) and \(\gamma=\frac{1}{2\beta}(\beta-1)\)

(2) \(\beta=\frac{1}{2\gamma}(\alpha+1)\) and \(\gamma=\frac{1}{2\alpha}(\alpha-1)\)

(3) \(\alpha=\frac{1}{2\beta}(\beta-1)\) and \(\gamma=\frac{1}{2\beta}(\beta+1)\)

(4) \(\beta=\frac{1}{2\gamma}(\alpha-1)\) and \(\gamma=\frac{1}{2\alpha}(\alpha+1)\)

Check Answer

Option

Q.No:17 CSIR June-2018

A particle moves in the one-dimensional potential \(V(x)=\alpha x^6\), where \(\alpha>0\) is a constant. If the total energy of the particle is \(E\), its time period in a periodic motion is proportional to

(1) \(E^{-1/3}\)

(2) \(E^{-1/2}\)

(3) \(E^{1/3}\)

(4) \(E^{1/2}\)

Check Answer

Option 1

Q.No:18 CSIR June-2018

The Hamiltonian of a one-dimensional system is \(H=\frac{xp^2}{2m}+\frac{1}{2}kx\), where \(m\) and \(k\) are positive constants. The corresponding Euler-Lagrange equation for the system is

(1) \(m\ddot{x}+k=0\)

(2) \(m\ddot{x}+2\dot{x}+kx^2=0\)

(3) \(2mx\ddot{x}-m\dot{x}^2+kx^2=0\)

(4) \(mx\ddot{x}+2m\dot{x}^2+kx^2=0\)

Check Answer

Option 3

Q.No:19 CSIR Dec-2018

The Hamiltonian of a classical one-dimensional harmonic oscillator is \(H=\frac{1}{2}(p^2+x^2)\), in suitable units. The total time derivative of the dynamical variable \((p+\sqrt{2}x)\) is

(1) \(\sqrt{2}p-x\)

(2) \(p-\sqrt{2}x\)

(3) \(p+\sqrt{2}x\)

(4) \(x+\sqrt{2}p\)

Check Answer

Option 1

Q.No:20 CSIR Dec-2018

A one-dimensional system is described by the Hamiltonian \(H=\frac{p^2}{2m}+\lambda |x|\) (where \(\lambda> 0\)). The ground state energy varies as a function of \(\lambda\) as

(1) \(\lambda^{5/3}\)

(2) \(\lambda^{2/3}\)

(3) \(\lambda^{4/3}\)

(4) \(\lambda^{1/3}\)

Check Answer

Option 2

Q.No:21 CSIR June-2019

A particle of mass \(m\) moves in one dimension in the potential \(V(x)=kx^4\), (\(k>0\)). At time \(t=0\), the particle starts from rest at \(x=A\). For bounded motion, the time period of its motion is

(1) proportional to \(A^{-1/2}\)

(2) proportional to \(A^{-1}\)

(3) independent of \(A\)

(4) not well-defined (the system is chaotic)

Check Answer

Option 2

Q.No:22 CSIR Dec-2019

A block of mass \(m\), attached to a spring, oscillates horizontally on a surface. The coefficient of friction between the block and the surface is \(\mu\). Which of the following trajectories best describes the motion of the block in the phase space (\(xp_x\)-plane)?

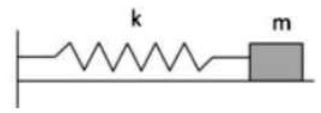
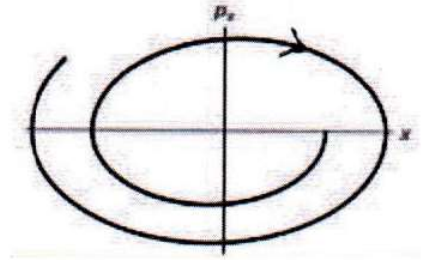
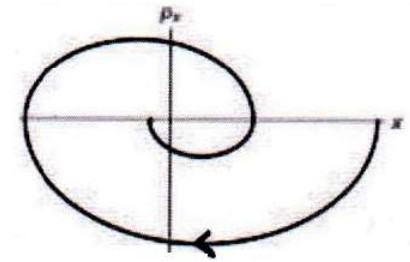
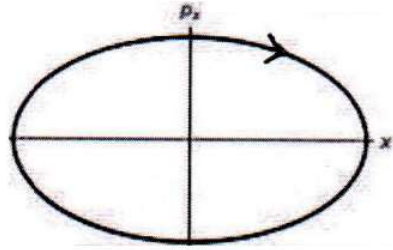
Check Answer

Option 2

Q.No:23 CSIR Dec-2019

The generator of the infinitesimal canonical transformation \(q\to q'=(1+\epsilon)q\) and \(p\to p'=(1-\epsilon)p\) is

(1) \(q+p\)

(2) \(qp\)

(3) \(\frac{1}{2}(q^2-p^2)\)

(4) \(\frac{1}{2}(q^2+p^2)\)

Check Answer

Option 2

Q.No:24 CSIR Dec-2019

The Hamiltonian of a system with two degrees of freedom is \(H=q_1 p_1-q_2 p_2+aq_1^2\), where \(a>0\) is a constant. The function \(q_1 q_2+\lambda p_1 p_2\) is a constant of motion only if \(\lambda\) is

(1) \(0\)

(2) \(1\)

(3) \(-a\)

(4) \(a\)

Check Answer

Option 1

Q.No:25 Assam CSIR Dec-2019

A particle of mass \(m\) oscillates in a one-dimensional potential \(V(x)=gx^4\), where \(g\) is a constant. If the amplitude of oscillation is doubled, then the ratio of the new time period to the old one is

(1) \(\frac{1}{2}\)

(2) \(1\)

(3) \(2\)

(4) \(\frac{1}{\sqrt{2}}\)

Check Answer

Option 1

Q.No:26 Assam CSIR Dec-2019

The mechanical momentum of a particle carrying a charge \(e\) in a magnetic field \(\vec{B}(\vec{r})\), is denoted by \(\vec{\pi}(\vec{r}, \vec{p})=\vec{p}-e\vec{A}(\vec{r})\) where \(\vec{\nabla}\times \vec{A}=\vec{B}\) and \(\vec{p}\) is the momentum canonically conjugate to \(\vec{r}\). If the Poisson bracket of \(x_i\) and \(p_j\) is \(\{x_i, p_j\}=\delta_{ij}\), then the Poisson bracket \(\{\pi_x, \pi_y\}\) is

(1) \(0\)

(2) \(\frac{e}{2}(B_x+B_y)\)

(3) \(\frac{e}{2}(B_x-B_y)\)

(4) \(eB_z\)

Check Answer

Option 4

Q.No:27 CSIR June-2020

Consider a particle with total energy \(E\) moving in one dimension in a potential \(V(x)\) as shown in the figure below.

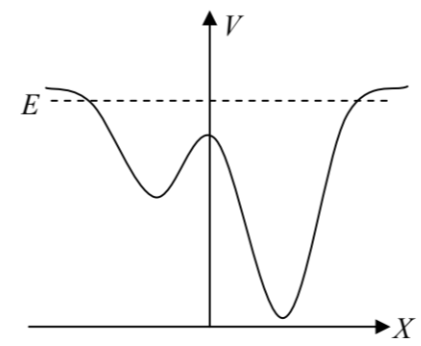
Which of the following figures best represents the orbit of the particle in the phase space?

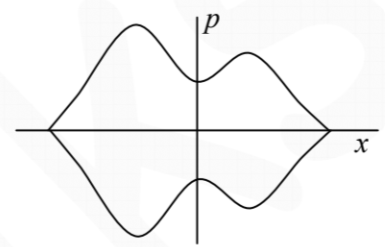
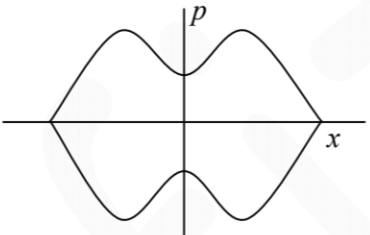
Check Answer

Option a

Q.No:28 CSIR Feb-2022

A particle in one dimension executes oscillatory motion in a potential \(V(x)=A|x|\), where \(A > 0\) is a constant of appropriate dimension. If the time period \(T\) of its oscillation depends on the total energy \(E\) as \(E^a\) , then the value of \(a\) is

(1) \(1/3\)

(2) \(1/2\)

(3) \(2/3\)

(4) \(3/4\)

Check Answer

Option 2

Q.No:29 CSIR Sep-2022

The Lagrangian of a particle n one dimension is \[ L=\frac{m}{2} \dot{x}^2-ax^2-V_0 e^{-10x} \] where \(a\) and \(V_0\) are positive constants. The best qualitative representation of a trajectory in phase space is

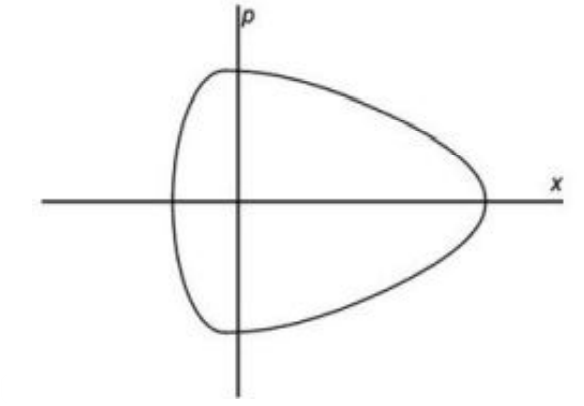
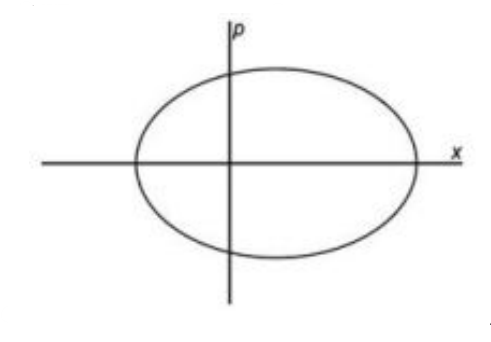
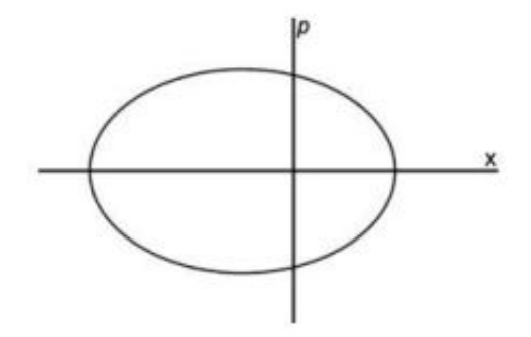
Check Answer

Option 2

Q.No:30 CSIR June-2023

For the transformation \(x\rightarrow X=\frac{\alpha p}{x}, p\rightarrow P=\beta x^2\) between conjugate pairs of a coordinate and its momentum, to be canonical, the constants \(\alpha\) and \(\beta\) must satisfy

1) \(1+\frac{1}{2}\alpha \beta=0 \)

2) \(1-\frac{1}{2}\alpha\beta=0 \)

3) \(1+2\alpha\beta=0 \)

4) \(1-2\alpha\beta=0 \)

Check Answer

Option 3

Q.No:31 CSIR June-2023

The Hamiltonian of a two particle system is \(H=p_1p_2+q_1q_2\), where \(q_1\) and \(q_2\) are generalized coordinates and \(p_1\) and \(p_2\) are the respective canonical momenta. The Lagrangian of this system is

1) \(\dot{q_1}\dot{q_2}+q_1q_2\)

2) \(-\dot{q_1}\dot{q_2}+q_1q_2\)

3) \(-\dot{q_1}\dot{q_2}-q_1q_2\)

4) \(\dot{q_1}\dot{q_2}-q_1q_2\)

Check Answer

Option 4

Q.No:32 CSIR Dec-2023

The 1-dimensional Hamiltonian of a classical particle of mass \( m \) is \[ H = \frac{p^2}{2m} e^{-x/a} + V(x), \] where \( a \) is a constant with appropriate dimensions. The corresponding Lagrangian is,

1) \( \frac{m}{2} \left(\frac{dx}{dt}\right)^2 e^{x/a} - V(x) \)

2) \( \frac{m}{2} \left(\frac{dx}{dt}\right)^2 e^{-x/a} - V(x) \)

3) \( \frac{3m}{2} \left(\frac{dx}{dt}\right)^2 e^{x/a} - V(x) \)

4) \( \frac{3m}{2} \left(\frac{dx}{dt}\right)^2 e^{-x/a} - V(x) \)

Check Answer

Option 1

Q.No:33 CSIR Dec-2023

A canonical transformation from the phase space coordinates \((q,p)\) to \((Q,P)\) is generated by the function \[ \psi(p, Q) = \frac{p^2}{2\omega} \tan 2\pi Q, \] where \(\omega\) is a positive constant. The function \(\psi(p, Q)\) is related to \(F(q, Q)\) by the Legendre transform \(\psi = pq - F\), where \(F\) is defined by \(dF = pdq - PdQ\). If the solution for \((P,Q)\) is \[ P(t) = \frac{\omega}{4\pi} t^2, \quad Q(t) = Q_0 = \text{constant}, \] where \(t\) is time, then the solution for \((p,q)\) variables can be written as

1) \( p = \frac{\omega t}{2\pi} \cos 2\pi Q_0, \quad q = \frac{t}{2\pi} \sin 2\pi Q_0 \)

2) \( p = -\frac{\omega t}{2\pi} \cos 2\pi Q_0, \quad q = \frac{t}{2\pi} \sin 2\pi Q_0 \)

3) \( p = \frac{\omega t}{2\pi} \sin 2\pi Q_0, \quad q = \frac{t}{2\pi} \cos 2\pi Q_0 \)

4) \( p = -\frac{\omega t}{2\pi} \sin 2\pi Q_0, \quad q = \frac{t}{2\pi} \cos 2\pi Q_0 \)

Check Answer

Option 1

Q.No:34 CSIR Dec-2023

A Lagrangian is given by \[ L = \frac{1}{2}m(\dot{x}^2 + \dot{y}\dot{z} + \dot{z}^2) - \alpha(2x + 3y + z). \] The conserved momentum is

1) \( m[2\dot{x} + \dot{z}] \)

2) \( m[2\dot{x} + \dot{y} + \dot{z}] \)

3) \( m\left[\dot{x} + \frac{3}{2}\dot{y} + \frac{1}{2}\dot{z}\right] \)

4) \( m[2\dot{x} + 3\dot{z}] \)

Check Answer

Option 2

Q.No:35 CSIR June-2024

For a simple harmonic oscillator, the Lagrangian is given by \[ L = \frac{1}{2} \dot{q}^2 - \frac{1}{2} q^2 \] If \(H(q,p)\) is the Hamiltonian of the system and \(A(p,q) = \frac{1}{\sqrt{2}} (p + iq)\), the Poisson bracket \(\{A, H\}\) is

1) \(iA\)

2) \(A^*\)

3) \(-iA^*\)

4) \(-iA\)

Check Answer

Option 1

Q.No:36 CSIR June-2024

Two non-interacting classical particles having masses \(m_1\) and \(m_2\) are moving in a one-dimensional box of length \(L\). For total energy not exceeding a given value \(E\), the phase space "volume" is given by

1) \(\pi L^2 E \left(\frac{m_1 m_2}{m_1 + m_2} \right)\)

2) \(\pi L^2 E \sqrt{m_1 m_2}\)

3) \(2\pi L^2 E \left(\frac{m_1 m_2}{m_1 + m_2} \right)\)

4) \(2\pi L^2 E \sqrt{m_1 m_2}\)

Check Answer

Option 4

Q.No:37 CSIR June-2024

The evolution of the dynamical variables \( x(t) \) and \( p(t) \) is given by \[ \dot{x} = ax \] \[ \dot{p} = -p \] where \( a \) is a constant. The trajectory in \( (x, p) \) space for \( -1 < a < 0 \) is best described by:

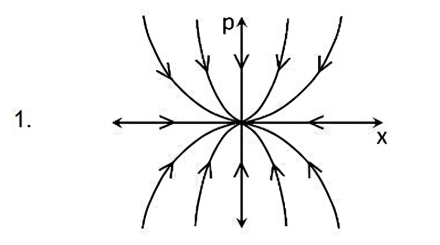
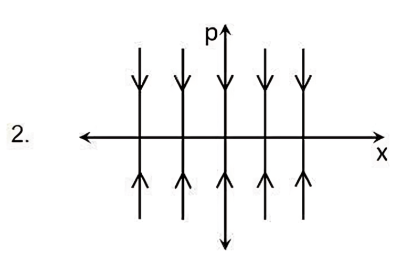
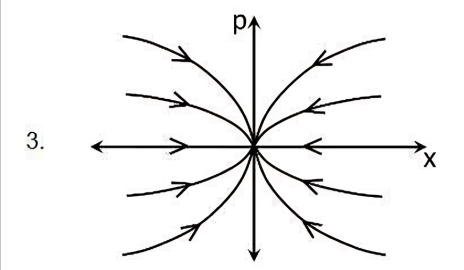
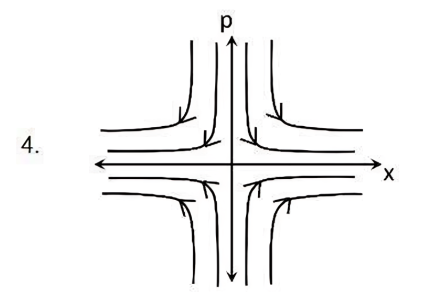
Check Answer

Option 1

Q.No:38 CSIR Dec-2024

The Lagrangian of a system is \[ L = \frac{15}{2} m \dot{x}^2 + 6m \dot{x}\dot{y} + 3m \dot{y}^2 - mg(x + 2y). \] Which one of the following quantities is conserved?

1) \(12\dot{x} + 3\dot{y}\)

2) \(12\dot{x} - 3\dot{y}\)

3) \(3\dot{x} - 12\dot{y}\)

4) \(3\dot{x} + 3\dot{y}\)

Check Answer

Option 1

Q.No:39 CSIR Dec-2024

For the canonical transformation \[ Q = \ln\!\left(1 + q^{1/2}\cos p\right), \qquad P = 2 q^{1/2}\left(1 + q^{1/2}\cos p\right)\sin p, \] the generating function is

1) \(- (e^{Q} - 1)^2 \cot p\)

2) \((e^{Q} - 1)^2 \cot p\)

3) \((e^{Q} - 1)^2 \tan p\)

4) \(- (e^{Q} - 1)^2 \tan p\)

Check Answer

Option 4

Q.No:40 CSIR June-2025

The Hamiltonian of a system is given by \[ H(x,p) = -\sqrt{p^{2} + V^{2}(x)}, \] where \(x\) and \(p\) are the generalized coordinate and momentum respectively, and \(V(x) \ge 0\). The corresponding Lagrangian is

1) \(- V(x)\sqrt{1-\dot{x}^{2}}\)

2) \(- \frac{V(x)}{\sqrt{1-\dot{x}^{2}}}\)

3) \(V(x)\sqrt{1-\dot{x}^{2}}\)

4) \(\frac{V(x)}{\sqrt{1-\dot{x}^{2}}}\)

Check Answer

Option 3

Q.No:41 CSIR June-2025

For a free particle of mass \(m\), consider the following time-dependent quantity in phase space \[ Q = \frac{q p}{m} - \frac{p^{2} t}{m^{2}}, \] where \(q\) and \(p\) are the canonically conjugate position and momentum coordinates respectively. Then \(\frac{dQ}{dt}\) is given by

1) \(0\)

2) \(\frac{p^{2}}{m^{2}}\)

3) \(-\frac{p^{2}}{m^{2}}\)

4) \(\frac{q p}{m t}\)