Q.No:1 JEST-2014
A double pendulum consists of two equal masses \(m\) suspended by two strings of length \(l\). What is the Lagrangian of this system for oscillations in a plane? Assume the angles \(\theta_1, \theta_2\) made by the two strings are small (you can use \(\cos{\theta}=1-\theta^2/2\)).
\({\bf Note:}\) \(\omega_0=\sqrt{g/l}\).
(a)
\(L\approx ml^2\left(\dot{\theta}_1^2+\frac{1}{2}\dot{\theta}_2^2-\omega_0^2\theta_1^2-\frac{1}{2}\omega_0^2\theta_2^2\right)\)
(b)
\(L\approx ml^2\left(\dot{\theta}_1^2+\frac{1}{2}\dot{\theta}_2^2+\dot{\theta}_1\dot{\theta}_2-\omega_0^2\theta_1^2-\frac{1}{2}\omega_0^2\theta_2^2\right)\)
(c)
\(L\approx ml^2\left(\dot{\theta}_1^2+\frac{1}{2}\dot{\theta}_2^2-\dot{\theta}_1\dot{\theta}_2-\omega_0^2\theta_1^2-\frac{1}{2}\omega_0^2\theta_2^2\right)\)
(d)
\(L\approx ml^2\left(\frac{1}{2}\dot{\theta}_1^2+\frac{1}{2}\dot{\theta}_2^2+\dot{\theta}_1\dot{\theta}_2-\omega_0^2\theta_1^2-\omega_0^2\theta_2^2\right)\)
Check Answer
Option b
Q.No:2 JEST-2014
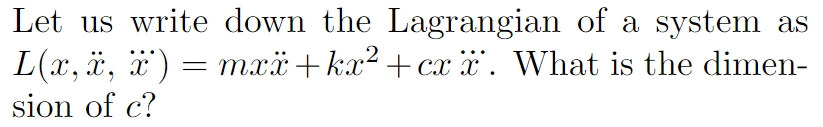
(a)
\(MLT^{-3}\)
(b)
\(MT^{-2}\)
(c)
\(MT\)
(d)
\(ML^2 T^{-1}\)
Check Answer
Option c
Q.No:3 JEST-2015
A bike stuntman rides inside a well of frictionless surface given by \(z=a(x^2+y^2)\), under the action of gravity acting in the negative \(z\) direction. \(\vec{g}=-g\hat{z}\) What speed should he maintain to be able to ride at a constant height \(z_0\) without falling down?
(a)
\(\sqrt{gz_0}\)
(b)
\(\sqrt{3gz_0}\)
(c)
\(\sqrt{2gz_0}\)
(d)
The biker will not be able to maintain a constant height, irrespective of speed.
Check Answer
Option c
Q.No:4 JEST-2015
The Lagrangian of a particle is given by \(L=\dot{q}^2-q\dot{q}\). Which of the following statements is true?
(a)
This is a free particle
(b)
The particle is experiencing velocity dependent damping
(c)
The particle is executing simple harmonic motion
(d)
The particle is under constant acceleration.
Check Answer
Option a
Q.No:5 JEST-2016
A hoop of radius \(a\) rotates with constant angular velocity \(\omega\) about the vertical axis as shown in the figure. A bead of mass \(m\) can slide on the hoop without friction. If \(g<\omega^2 a\), at what angle \(\theta\) apart from \(0\) and \(\pi\) is the bead stationary ( i.e., \(\frac{d\theta}{dt}=\frac{d^2\theta}{dt^2}=0\))?
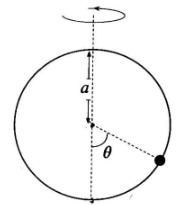
(A)
\(\tan{\theta}=\pi g/\omega^2 a\)
(B)
\(\sin{\theta}=g/\omega^2 a\)
(C)
\(\cos{\theta}=g/\omega^2 a\)
(D)
\(\tan{\theta}=g/\pi \omega^2 a\)
Check Answer
Option C
Q.No:6 JEST-2017
A possible Lagrangian for a free particle is
(A)
\(L=\dot{q}^2-q^2\).
(B)
\(L=\dot{q}^2-q\dot{q}\).
(C)
\(L=\dot{q}^2-q\).
(D)
\(L=\dot{q}^2-\frac{1}{q}\).
Check Answer
Option B
Q.No:7 JEST-2017
A bead of mass \(M\) slides along a parabolic wire described by \(z=2(x^2+y^2)\). The wire rotates with angular velocity \(\Omega\) about the \(z\)-axis. At what value of \(\Omega\) does the bead maintain a constant nonzero height under the action of gravity along \(-\hat{z}\)?
(A)
\(\sqrt{3g}\)
(B)
\(\sqrt{g}\)
(C)
\(\sqrt{2g}\)
(D)
\(\sqrt{4g}\)
Check Answer
Option D
Q.No:8 JEST-2017
A rod of mass \(m\) and length \(l\) is suspended from two massless vertical springs with a spring constants \(k_1\) and \(k_2\). What is the Lagrangian for the system, if \(x_1\) and \(x_2\) be the displacements from equilibrium position of the two ends of the rod?
(A)
\(\frac{m}{8}(\dot{x}_1^2+2\dot{x}_1\dot{x}_2+\dot{x}_2^2)-\frac{1}{2}k_1 x_1^2-\frac{1}{2}k_2 x_2^2\)
(B)
\(\frac{m}{2}(\dot{x}_1^2+\dot{x}_1\dot{x}_2+\dot{x}_2^2)-\frac{1}{4}(k_1+k_2)(x_1^2+x_2^2)\)
(C)
\(\frac{m}{6}(\dot{x}_1^2+\dot{x}_1\dot{x}_2+\dot{x}_2^2)-\frac{1}{2}k_1 x_1^2-\frac{1}{2}k_2 x_2^2\)
(D)
\(\frac{m}{4}(\dot{x}_1^2-2\dot{x}_1\dot{x}_2+\dot{x}_2^2)-\frac{1}{4}(k_1-k_2)(x_1^2+x_2^2)\)
Check Answer
Option C
Q.No:9 JEST-2018
A block of mass \(M\) is moving on a frictionless inclined surface of a wedge of mass \(m\) under the influence of gravity. The wedge is lying on a rigid frictionless horizontal surface. The configuration can be described using the radius vectors \(\vec{r}_1\) and \(\vec{r}_2\) shown in the figure. How many constraints are present and what are the types?

(A)
One constraint; holonomic and scleronomous
(B)
Two constraints; Both are holonomic; one is scleronomous and rheonomous
(C)
Two constraints; Both are scleronomous; one is holonomic and the other is non-holonomic.
(D)
Two constraints; Both are holonomic and scleronomous
Check Answer
Option D
Q.No:10 JEST-2018
Consider the Lagrangian
\[
L=1-\sqrt{1-\dot{q}^2}-\frac{q^2}{2}
\]
of a particle executing oscillations whose amplitude is \(A\). If \(p\) denotes the momentum of the particle, then \(4p^2\) is
(A)
\((A^2-q^2)(4+A^2-q^2)\)
(B)
\((A^2+q^2)(4+A^2-q^2)\)
(C)
\((A^2-q^2)(4+A^2+q^2)\)
(D)
\((A^2+q^2)(4+A^2+q^2)\)
Check Answer
Option A
Q.No:11 JEST-2019
Consider the motion of a particle in two dimensions given by the Lagrangian
\[
L=\frac{m}{2}(\dot{x}^2+\dot{y}^2)-\frac{\lambda}{4}(x+y)^2,
\]
where \(\lambda>0\). The initial conditions are given as \(y(0)=0, x(0)=42\) meters, \(\dot{x}(0)=\dot{y}(0)=0\). What is the value of \(x(t)-y(t)\) at \(t=25\) seconds in meters?
Check Answer
Ans 42
Q.No:12 JEST-2020
A particle is to slide along the horizontal circular path on the inner surface of the funnel as shown in the figure. The surface of the funnel is frictionless. What must be the speed of the particle (in terms of \(r\) and \(\theta\)) if it is to execute this motion?
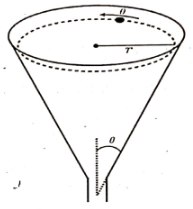
(A)
\(\sqrt{rg\sin{\theta}}\)
(B)
\(\sqrt{rg\cos{\theta}}\)
(C)
\(\sqrt{rg\tan{\theta}}\)
(D)
\(\sqrt{rg\cot{\theta}}\)
Check Answer
Option D
Q.No:13 JEST-2021
A particle of mass \(m\) is subject to the potential \(V(x, y, t)=K(x^2+y^2)\), where \((x, y)\) are the Cartesian coordinates of the particle and \(K\) is a constant. Which one of the following quantities is a constant of motion?
(A)
\(\dot{y}x+\dot{x}y\)
(B)
\(\dot{y}x-\dot{x}y\)
(C)
\(\dot{y}+\dot{x}\)
(D)
\(\dot{y}y+\dot{x}x\)
Check Answer
Option B
Q.No:14 JEST-2022
Two uniform rods of length \(1 m\) are connected to a friction-less hinge A. The hinge is held at a height and the other ends of the rods rests on a friction-less plane, such that the angle between the rods is \(2\pi/3\). If the hinge is released from the rest, what is the speed of the hinge when it hits the floor? [Acceleration due to gravity is \(9.81 ms^{-2}\)]

Check Answer
Ans 1.92
Q.No:15 JEST-2023
The action corresponding to the motion of a particle in one dimension is:
\[S=\int_{t_i} ^{t_f} dt \left[ \frac{1}{2} m \dot{x}^2-V (x) +\alpha x \ddot{x} +\beta x \dot{x} \right] \]
where \(m\) is the mass of the particle, \(\alpha, \beta\) are constants, and \(V (x)\) is a potential which is a function of \(x\). The position and velocity are held fixed at the end points of the trajectory. The
equation of motion of the particle is
(a) \((2 \alpha+m) \ddot{x}-\frac{dV}{dx}=0\)
(b) \((2 \alpha-m) \ddot{x}+ \beta \dot{x}-\frac{dV}{dx}=0\)
(c) \((2 \alpha-m) \ddot{x}- \beta \dot{x}-\frac{dV}{dx}=0\)
(d) \((2 \alpha-m) \ddot{x}-\frac{dV}{dx}=0\)
Check Answer
option d
Q.No:16 JEST-2024
Consider a mass-pulley system as shown in the figure. The heights of the blocks as measured from the ceiling are \(x_1\) and \(x_2\), as shown in the figure.
What is the constraint between \(x_1\) and \(x_2\)?

What is the constraint between \(x_1\) and \(x_2\)?
(a) \(x_2 + 2x_1 = \text{constant}.\)
(b) \(x_2 - x_1 = \text{constant}.\)
(c) \(x_2 + x_1 = \text{constant}.\)
(d) They are unconstrained.
Check Answer
option a
Q.No:17 JEST-2024
Two classical particles moving in three dimensions interact via the potential
\[
V = K \left[ (x_1^2 + y_1^2) + (x_2^2 + y_2^2) + (z_1 - z_2)^2 \right],
\]
where \( K \) is a constant, and \( (x_1, y_1, z_1) \) and \( (x_2, y_2, z_2) \) are the Cartesian coordinates of the two particles. Let \( (p^x_1, p^y_1, p^z_1) \) and \( (p^x_2, p^y_2, p^z_2) \) be the components of the linear momenta of the two particles, and \( (L^x_1, L^y_1, L^z_1) \) and \( (L^x_2, L^y_2, L^z_2) \) the components of the corresponding angular momenta. Which of the following statements is true?
(a) \( L^z_1, L^z_2, \) and \( (p^z_1 + p^z_2) \) are conserved.
(b) \( L^z_1 \) and \( L^z_2 \) are not separately conserved but \( L^z_1 + L^z_2 \) is conserved.
(c) \( (L^x_1 + L^x_2), (L^y_1 + L^y_2), (L^z_1 + L^z_2) \) are conserved.
(d) \( (L^x_1 + L^x_2) \) and \( (L^y_1 + L^y_2) \) are conserved.
Check Answer
option a
Q.No:18 JEST-2024
A classical system has the following action:
\[
S = \int (\dot{q}^2 + \alpha q\dot{q} + \beta q^2\dot{q})dt ,
\]
where \( q \) is the generalized coordinate, and \( \alpha \) and \( \beta \) are constants. Which of the following statements is true about the dynamics of the system?
(a) The dynamics is independent of \( \alpha \) and \( \beta \).
(b) The dynamics depends only on \( \alpha \).
(c) The dynamics depends only on \( \beta \).
(d) The dynamics depends on ratio \( \alpha / \beta \).
Check Answer
option a
Q.No:19 JEST-2025
The Lagrangian of a two-dimensional system is given by
\[
L = \frac{1}{2} m \left(\dot{x}^{2} + \dot{y}^{2}\right)
- k (x^{2} + y^{2})^{-1.5}.
\]
Which of the following is/are the constant(s) of motion?
a) Angular momentum only
b) Energy only
c) Energy and angular momentum
d) None of the others
Check Answer
option c
Q.No:1 TIFR-2013
A ball of mass \(m\) slides under gravity without friction inside a semicircular depression of radius \(a\) inside a fixed block placed on a horizontal surface, as shown in the figure. The equation of motion of the ball in the \(x\)-direction will be
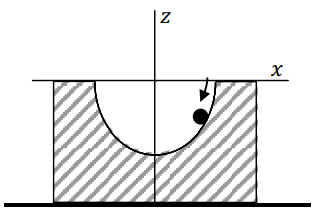
(a)
\(\ddot{x}=\frac{g}{a}x\sqrt{1-\frac{x^2}{a^2}}\)
(b)
\(\ddot{x}=\frac{g}{a}x\)
(c)
\(\ddot{x}=-\frac{g}{a}x\)
(d)
\(\ddot{x}=-\frac{g}{a}x\sqrt{1-\frac{x^2}{a^2}}\)
Check Answer
Option d
Q.No:2 TIFR-2015
A particle slides on the inside surface of a frictionless cone. The cone is fixed with its tip on the ground and its axis vertical, as shown in the figure on the right. The semi-vertex angle of the cone is \(\alpha\). If the particle moves in a circle of radius \(r_0\), without slipping downwards, the angular frequency \(\omega\) of this motion will be
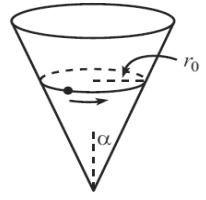
(a)
\(\sqrt{\frac{g}{r_0 \cos{\alpha}}}\)
(b)
\(\sqrt{\frac{g}{r_0 \sin{\alpha}}}\)
(c)
\(\sqrt{\frac{g}{r_0 \cot{\alpha}}}\)
(d)
\(\sqrt{\frac{g}{r_0 \tan{\alpha}}}\)
Check Answer
Option d
Q.No:3 TIFR-2017
A uniform solid sphere \(S_1\) of radius \(r\) and mass \(m\) is rolling without slipping on top of another sphere \(S_2\) of radius \(R\), as shown in the figure. Initially, \(S_1\) was at rest directly on top of \(S_2\), and then it started rolling down under the influence of gravity. The point of contact \(P\) subtends an instantaneous angle \(\theta\) from the topmost point \(N\) of the lower sphere at the centre of the lower sphere.

At what minimum value of \(\theta\) will the spheres lose contact?
(a)
\(\cos^{-1}{\frac{5}{12}}\)
(b)
\(\cos^{-1}{\frac{5}{13}}\)
(c)
\(\cos^{-1}{\frac{2}{3}}\)
(d)
\(\cos^{-1}{\frac{12}{13}}\)
Check Answer
Option a
Q.No:4 TIFR-2018
A particle of mass \(m\) moving in one-dimension \(x\) is subjected to the Lagrangian
\[
L=\frac{1}{2}m(\dot{x}-\lambda x)^2
\]
where \(\lambda\) is a real constant. If it starts at the origin at \(t=0\), its motion corresponds to the equation (\(a\) is a constant)
(a)
\(x=a\exp{\lambda t}\)
(b)
\(x=a\{1-\exp{(-\lambda t)}\}\)
(c)
\(x=a\sin{\lambda t}\)
(d)
\(x=a\sinh{\lambda t}\)
Check Answer
Option d
Q.No:5 TIFR-2018
The Hamiltonian of a particle of charge \(q\) and mass \(m\) in an electromagnetic field is given by
\[
H=\frac{1}{2m}|\vec{p}-q\vec{A}(\vec{x}, t)|^2+q\varphi(\vec{x}, t)
\]
where \((\varphi, \vec{A})\) are the electromagnetic potentials. Clearly this Hamiltonian changes under a gauge transformation
\[
\varphi\to \varphi-\frac{\partial \chi}{\partial t} \vec{A}\to \vec{A}+\vec{\nabla}\chi
\]
where \(\chi(\vec{x}, t)\) is a gauge function. Nevertheless the motion of the particle is not affected because
(a)
the Lagrangian does not change under the gauge transformation.
(b)
the motion of the particle is correctly described only in the Lorenz gauge.
(c)
the action of the particle changes only by surface terms which do not vary.
(d)
the Lorentz force is modified to balance the effect of the gauge transformation.
Check Answer
Option c
Q.No:6 TIFR-2021
A particle of mass \(m\) moves in a plane \((r, \theta)\) under the influence of a force
\[
\vec{F}=\frac{mk}{r^3}(x\hat{r}+y\hat{\theta})
\]
where \(x=r\cos{\theta}\) and \(y=r\sin{\theta}\), while \(k\) is a constant. The Lagrangian for this system is
(a)
\(L=\frac{1}{2}m\left(\dot{r}^2+r^2\dot{\theta}^2-\frac{kx}{r^2}\right)\)
(b)
\(L=\frac{1}{2}m\left(\dot{x}^2+\dot{y}^2-\frac{ky}{r^2}\right)\)
(c)
\(L=\frac{1}{2}m\left(\frac{\dot{r}^2}{r}+r\dot{\theta}^2-\frac{kxy}{r}\right)\)
(d)
\(L=\frac{1}{2}m\left(\dot{x}^2+\dot{y}^2+\frac{kx}{r^2}\right)\)
Check Answer
Option a
Q.No:7 TIFR-2021
Consider a diatomic molecule of oxygen which is rotating in the \(xy\)-plane about the \(z\) axis. The \(z\) axis passes through the centre of the molecule and is perpendicular to its length. At room temperature, the average separation between the two oxygen atoms is \(1.21\times 10^{-10} \hspace{1mm}\text{m}\) (the atoms are treated as point masses). The molar mass of oxygen is \(16 \hspace{1mm}\text{gm}/\text{mol}\).

If the angular velocity of the molecule about the \(z\) axis is \(2\times 10^{12} \hspace{1mm}\text{rad}/\text{s}\), its rotational kinetic energy will be closet to
(a)
\(3.89\times 10^{-22} \hspace{1mm}\text{Joule}\)
(b)
\(7.78\times 10^{-22} \hspace{1mm}\text{Joule}\)
(c)
\(15.56\times 10^{-22} \hspace{1mm}\text{Joule}\)
(d)
\(1.95\times 10^{-22} \hspace{1mm}\text{Joule}\)
Check Answer
Option a
Q.No:7 TIFR-2021
Two equal masses \( m \) are connected with a massless string. The first mass is initially set in a uniform circular motion with speed \( v_i \), at a radius \( r_i \) on top of a table while the second mass hangs vertically on the string which passes through a hole in the center of the table (C), as shown in the figure below.
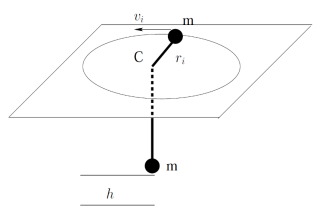
The system is released with this initial configuration and the second mass starts falling. What is the net speed of the first mass when the second mass has fallen a height \( h \) (smaller than \( r_i \))?
(Assume that there is no friction and that the string always remains tight.)
(a) \( \sqrt{gh + \frac{1}{2} v_i^2 \left[ 1 + \left( \frac{r_i^2}{(r_i - h)^2} \right) \right]} \)
(b) \( \sqrt{gh + \frac{1}{2} v_i^2 \left[ 1 + \frac{r_i}{(r_i - h)} \right]} \)
(b) \( \sqrt{gh + \frac{1}{2} v_i^2 \left[ 1 + \frac{r_i}{(r_i - h)} \right]} \)
(c) \( \sqrt{gh + \frac{1}{2} v_i^2 \left[ 1 + \left( \frac{(r_i - h)^2}{r_i^2} \right) \right]} \)
(d) \( \sqrt{gh + \frac{1}{2} v_i^2 \left[ 1 + \frac{(r_i - h)}{r_i} \right]} \)
Check Answer
Option a
Q.No:8 TIFR-2025
A massless rigid rod of length \(L\) is suspended with an ideal spring of spring
constant \(k\) at one end \(P\), and by a hinge on the other end \(Q\).
The rest length of the spring is zero. A mass \(m\) is suspended from the
mid-point of the rod. This results in tilting of the rod by angle \(\theta\).
What is the angle \(\theta\)?
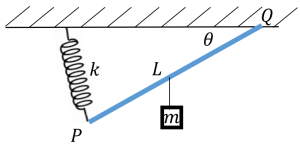
a) \(\tan^{-1}\!\left(\frac{mg}{2kL}\right)\)
b) \(\sin^{-1}\!\left(\frac{mg}{2kL}\right)\)
c) \(\cos^{-1}\!\left(\frac{mg}{kL}\right)\)
d) \(\sec^{-1}\!\left(\frac{mg}{kL}\right)\)
Check Answer
Option a
Q.No:9 TIFR-2025
A composite pendulum consists of two massless rods and a weight \(m\).
The two rods are connected by a hinge \(H'\).
The other end of the first rod is connected to the ceiling by a hinge \(H\).
The rods can move freely about \(H, H'\) in the \(xy\)-plane.
What is the Lagrangian of the system?
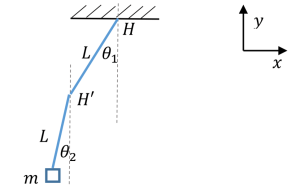
a) \(\frac{L^{2} m}{2}\left(\dot{\theta}_1^{2} + \dot{\theta}_2^{2}
+ 2 \dot{\theta}_1 \dot{\theta}_2 \cos(\theta_1 - \theta_2)\right)
+ g L m (\cos\theta_1 + \cos\theta_2)\)
b) \(\frac{L^{2} m}{2}\left(\dot{\theta}_1^{2} + \dot{\theta}_2^{2}\right)
+ g L m (\cos\theta_1 + \cos\theta_2)\)
c) \(\frac{L^{2} m}{2}\left(\dot{\theta}_1^{2} + \dot{\theta}_2^{2}
+ 2 \dot{\theta}_1 \dot{\theta}_2 \sin(\theta_1 - \theta_2)\right)
- g L m (\cos\theta_1 + \cos\theta_2)\)
d) \(\frac{L^{2} m}{2}\left(\dot{\theta}_1^{2} + \dot{\theta}_2^{2}
- 2 \dot{\theta}_1 \dot{\theta}_2 \cos(\theta_1 - \theta_2)\right)
- g L m (\cos\theta_1 + \cos\theta_2)\)

where do i find solutions to these problems?
JUST 2015 4)
Q.No.1 Discussion (JEST) :
Solution part 1
Solution part 2
Q.No.2 Discussion (JEST) :
Q.No.3 Discussion (JEST) :
solution
continued
Q.No.4 Discussion (JEST) :
Answer: A
Answer:A
Q.No.5 Discussion (JEST) :
Jest Q5
.
page 2
Q.No.6 Discussion (JEST) :
ans option B
Q.No.7 Discussion (JEST) :
Q.No.8 Discussion (JEST) :
Q8 Page 1
Q8 page 2
Q.No.9 Discussion (JEST) :
Q.No.10 Discussion (JEST) :
Q.No.11 Discussion (JEST) :
Ans
Q.No.12 Discussion (JEST) :
Q.No.13 Discussion (JEST) :
Q.No.14 Discussion (JEST) :
Q.No.15 Discussion (JEST) :
Q.No.16 Discussion (JEST) :
Q.No.1 Discussion (TIFR) :
Answer
Ans
Q.No.2 Discussion (TIFR) :
Solution
Q.No.3 Discussion (TIFR) :
Q.No.4 Discussion (TIFR) :
Q no 4 soln
Q.No.5 Discussion (TIFR) :
Q.No.6 Discussion (TIFR) :
solution
Q.No.7 Discussion (TIFR) :
Option D
Q.No.8 Discussion (TIFR) :
Q.No.9 Discussion (TIFR) :
Q.No.10 Discussion (TIFR) :