Q.No:1 GATE-2013
At a surface current, which one of the magnetostatic boundary condition is NOT CORRECT?
(A)
Normal component of the magnetic field is continuous.
(B)
Normal component of the magnetic vector potential is continuous.
(C)
Tangential component of the magnetic vector potential is continuous.
(D)
Tangential component of the magnetic vector potential is not continuous.
Check Answer
Option D
Q.No:2 GATE-2013
In a constant magnetic field of \(0.6\) Tesla along the \(z\) direction, find the value of the path integral \(\oint \vec{A}\cdot \vec{dl}\) in the units of (Tesla \({m^2}\)) on a square loop of side length (\(1/\sqrt{2}\)) meters. The normal to the loop makes an angle of \(60^{\circ}\) to the \(z\)-axis, as shown in the figure. The answer should be up to two decimal places ___________

Check Answer
Ans 0.15
Q.No:3 GATE-2014
The value of the magnetic field required to maintain non-relativistic protons of energy \(1 MeV\) in a circular orbit of radius \(100 mm\) is ___________ Tesla. (Given: \(m_p=1.67\times 10^{-27} kg, e=1.6\times 10^{-19} C\))
Check Answer
Ans 1.41-1.47
Q.No:4 GATE-2015
Given that the magnetic flux through the closed loop \(PQRSP\) is \(\phi\). If \(\int_{P}^{R} \vec{A}\cdot \vec{dl}=\phi_1\) along \(PQR\), the value of \(\int_{P}^{R} \vec{A}\cdot \vec{dl}\) along \(PSR\) is

(A)
\(\phi-\phi_1\)
(B)
\(\phi_1-\phi\)
(C)
\(-\phi_1\)
(D)
\(\phi_1\)
Check Answer
Option B
Q.No:5 GATE-2016
Which of the following magnetic vector potentials gives rise to a uniform magnetic field \(B_0 \hat{k}\)?
(A)
\(B_0 z\hat{k}\)
(B)
\(-B_0 x\hat{j}\)
(C)
\(\frac{B_0}{2}(-y\hat{i}+x\hat{j})\)
(D)
\(\frac{B_0}{2}(y\hat{i}+x\hat{j})\)
Check Answer
Option C
Q.No:6 GATE-2016
The magnitude of the magnetic dipole moment associated with a square shaped loop carrying a steady current \(I\) is \(m\). If this loop is changed to a circular shape with the same current \(I\) passing through it, the magnetic dipole moment becomes \(\frac{pm}{\pi}\). The value of \(p\) is _______________-.
Check Answer
Ans 4
Q.No:7 GATE-2016
The \(x\)-\(y\) plane is the boundary between free space and a magnetic material with relative permeability \(\mu_r\). The magnetic field in the free space is \(B_x \hat{i}+B_z \hat{k}\). The magnetic field in the magnetic material is
(A)
\(B_x \hat{i}+B_z \hat{k}\)
(B)
\(B_x \hat{i}+\mu_r B_z \hat{k}\)
(C)
\(\frac{1}{\mu_r}B_x \hat{i}+B_z \hat{k}\)
(D)
\(\mu_r B_x \hat{i}+B_z \hat{k}\)
Check Answer
Option D
Q.No:8 GATE-2018
An infinitely long straight wire is carrying a steady current \(I\). The ratio of magnetic energy density at distance \(r_1\) to that at \(r_2\) (\(=2r_1\)) from the wire is __________.
Check Answer
Ans 4
Q.No:9 GATE-2019
A solid cylinder of radius \(R\) has total charge \(Q\) distributed uniformly over its volume. It is rotating about its axis with angular speed \(\omega\). The magnitude of the total magnetic moment of the cylinder is
(A)
\(QR^2 \omega\)
(B)
\(\frac{1}{2}QR^2 \omega\)
(C)
\(\frac{1}{4}QR^2 \omega\)
(D)
\(\frac{1}{8}QR^2 \omega\)
Check Answer
Option C
Q.No:10 GATE-2019
An infinitely long wire parallel to the \(x\)-axis is kept at \(z=d\) and carries a current \(I\) in the positive \(x\) direction above a superconductor filling the region \(z\leq 0\) (see figure). The magnetic field \(\vec{B}\) inside the superconductor is zero so that the field just outside the superconductor is parallel to its surface. The magnetic field due to this configuration at a point (\(x, y, z>0\)) is

(A)
\(\left(\frac{\mu_0 I}{2\pi}\right)\frac{-(z-d)\hat{j}+y\hat{k}}{[y^2+(z-d)^2]}\)
(B)
\(\left(\frac{\mu_0 I}{2\pi}\right)\left[\frac{-(z-d)\hat{j}+y\hat{k}}{y^2+(z-d)^2}+\frac{(z+d)\hat{j}-y\hat{k}}{y^2+(z+d)^2}\right]\)
(C)
\(\left(\frac{\mu_0 I}{2\pi}\right)\left[\frac{-(z-d)\hat{j}+y\hat{k}}{y^2+(z-d)^2}-\frac{(z+d)\hat{j}-y\hat{k}}{y^2+(z+d)^2}\right]\)
(D)
\(\left(\frac{\mu_0 I}{2\pi}\right)\left[\frac{y\hat{j}+(z-d)\hat{k}}{y^2+(z-d)^2}+\frac{y\hat{j}-(z+d)\hat{k}}{y^2+(z+d)^2}\right]\)
Check Answer
Option B
Q.No:11 GATE-2020
Far from the Earth, the Earth's magnetic field can be approximated as due to a bar magnet of magnetic pole strength \(4\times 10^{14} Am\). Assume this magnetic field is generated by a current carrying loop encircling the magnetic equator. The current required to do so is about \(4\times 10^n A\), where \(n\) is an integer. The value of \(n\) is ____________.
(Earth's circumference: \(4\times 10^7 m\))
Check Answer
Ans 7
Q.No:12 GATE-2021
Consider a solenoid of length \(L\) and radius \(R\), where \(R\ll L\). A steady-current flows through the solenoid. The magnetic field is uniform inside the solenoid and zero outside.

Among the given options, choose the one that best represents the variation in the magnitude of the vector potential, \((0, A_{\varphi}, 0)\) at \(z=L/2\), as a function of the radial distance (\(r\)) in cylindrical coordinates.
{Useful information: The curl of a vector \(\vec{F}\), in cylindrical coordinates is}
\[
\vec{\nabla}\times \vec{F}(r, \varphi, z)=\hat{r}\left[\frac{1}{r}\frac{\partial F_z}{\partial \varphi}-\frac{\partial F_{\varphi}}{\partial z}\right]\]
\[+\hat{\varphi}\left[\frac{\partial F_r}{\partial z}-\frac{\partial F_z}{\partial r}\right]+\hat{z}\frac{1}{r}\left[\frac{\partial (rF_{\varphi})}{\partial r}-\frac{\partial F_r}{\partial \varphi}\right]
\]


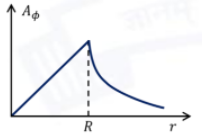

Check Answer
Option C
Q.No:13 GATE-2021
A material is placed in a magnetic field intensity \(H\). As a result, bound current density \(J_b\) is induced and magnetization of the material is \(M\). The magnetic flux density is \(B\). Choose the correct option(s) valid at the surface of the material.
(A)
\(\nabla. M=0\)
(B)
\(\nabla. B=0\)
(C)
\(\nabla. H=0\)
(D)
\(\nabla. J_b=0\)
Check Answer
Option B_D
Q.No:14 GATE-2021
Consider a cross-section of an electromagnet having an air-gap of \(5 cm\) as shown in the figure. It consists of a magnetic material (\(\mu=20000\mu_0\)) and is driven by a coil having \(NI-10^4A\), where \(N\) is the number of turns and \(I\) is the current in Ampere.

Ignoring the fringe fields, the magnitude of the magnetic field \(\vec{B}\) (in Tesla, rounded off to two decimal places) in the air-gap between the magnetic poles is ___________________.
Check Answer
Ans 0.24-0.26
Q.No:15 GATE-2016
Which of the following magnetic vector potentials gives rise to a uniform magnetic field \(B_0 \hat{k}\)?
(A)
\(B_0 z\hat{k}\)
(B)
\(-B_0 x\hat{j}\)
(C)
\(\frac{B_0}{2}(-y\hat{i}+x\hat{j})\)
(D)
\(\frac{B_0}{2}(y\hat{i}+x\hat{j})\)
Check Answer
Option A
Q.No:16 GATE-2023
Consider an isolated magnetized sphere of radius \(R\) with a uniform magnetization \(\vec{M}\) along the positive \(z\) direction, with the north and south poles of the sphere lying on the \(z\) axis. It is given that the magnetic field inside the sphere is \(\vec{B}=\frac{2\mu_0}{3} \vec{M}\) , where \(\mu_0\) is the permeability of vacuum. Which of the following statements is(are) CORRECT?
(A)
The bound volume current density is zero
(B)
The bound surface current density has maximum magnitude at the equator, where this magnitude equals \(|\vec{M}|\)
(C)
The auxiliary field \(\vec{H}=-\frac{2}{3} \vec{M}\)
(D)
Far from the sphere, the magnetic field is due to a dipole of moment \(\vec{m}\), where \(\frac{\vec{m}}{4\pi R^3}=\frac{B}{2\mu_0} \hat{z}\)
Check Answer
Option A , B , D
Q.No:17 GATE-2024
An infinitely long cylinder of radius \( R \) carries a frozen-in magnetization
\[
\vec{M} = k e^{-s} \hat{z},
\]
where \( k \) is a constant and \( s \) is the distance from the axis of the cylinder. The magnetic permeability of free space is \( \mu_0 \). There is no free current present anywhere. The magnetic flux density (\( \vec{B} \)) inside the cylinder is
(A) \( 0 \)
(B) \( \mu_0 k e^{-R} \hat{z} \)
(C) \( \mu_0 k e^{-s} \hat{z} \)
(D) \( \mu_0 k e^{-s} \left(\frac{R}{s}\right) \hat{z} \)
Check Answer
Option C
Q.No:18 GATE-2025
The wire loop shown in the figure carries a steady current \(I\). Each straight section of the loop has length \(d\). A part of the loop lies in the \(xy\)-plane and the other part is tilted at \(30^\circ\) with respect to the \(xz\)-plane. The magnitude of the magnetic dipole moment of the loop (in appropriate units) is
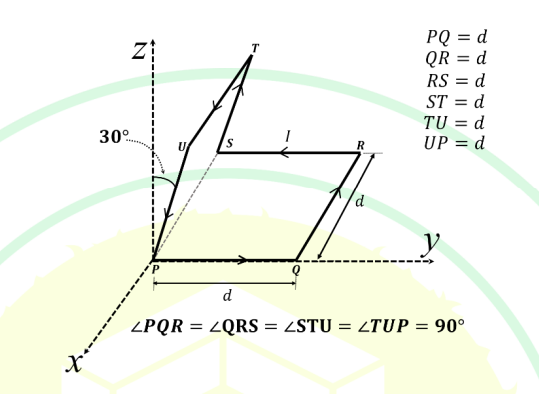
A)\(\sqrt{2}\,I d^{2}\)
B) \(2\,I d^{2}\)
C) \(\sqrt{3}\,I d^{2}\)
D) \(I d^{2}\)
Check Answer
Option D
Q.No:19 GATE-2025
A linear magnetic material in the form of a cylinder of radius \(R\) and length \(L\) is placed with its axis parallel to the \(z\)-axis. The cylinder has uniform magnetization \(M\hat{k}\). Which of the following option(s) is/are correct?
A) The magnetic field at any point outside the cylinder can be expressed as the gradient of a scalar function.
B) The bound volume current density is zero.
C) The surface current density on the curved surface is non-zero.
D) The surface current densities on the flat surfaces (top and bottom) are non-zero.
Check Answer
Option A,B,C
Q.No:1 CSIR Dec-2014
Ignoring the fringe fields, the magnitude of the magnetic field \(\vec{B}\) (in Tesla, rounded off to two decimal places) in the air-gap between the magnetic poles is ____________.

The ratio \(\ell/R\) of the pitch \(\ell\) to the radius \(R\) of the helical path is
(1)
\(\pi/2\)
(2)
\(4\pi\)
(3)
\(2\pi\)
(4)
\(\pi\)
Check Answer
Option 2
Q.No:2 CSIR June-2015
A proton moves with a speed of 300 m/s in
a circular orbit in the xy-plane in a magnetic field 1 tesla along the positive 2 direction. When an electric field of I V/m is applied along the positive y-direction. the centre of the circular orbit
(1)
remains stationary
(2)
moves at 1 m/s along the negative x-direction
(3)
moves at 1 m/s along the positive z-direction
(4)
moves at 1 m/s along the positive x direction.
Check Answer
Option 4
Q.No:3 CSIR Dec-2015
Given a uniform magnetic field \(\mathbf{B}=B_0 \hat{k}\) (where \(B_0\) is a constant), a possible choice for the magnetic vector potential \(\mathbf{A}\) is
(1)
\(B_0 y\hat{i}\)
(2)
\(-B_0 y\hat{i}\)
(3)
\(B_0(x\hat{j}+y\hat{i})\)
(4)
\(B_0(x\hat{i}-y\hat{j})\)
Check Answer
Option 4
Q.No:4 CSIR Dec-2015
A small magnetic needle is kept at \((0, 0)\) with its moment along the \(x\)-axis. Another small magnetic needle is at the point \((1, 1)\) and is free to rotate in the \(xy\)-plane. In equilibrium the angle \(\theta\) between their magnetic moments is such that
(1)
\(\tan{\theta}=1/3\)
(2)
\(\tan{\theta}=0\)
(3)
\(\tan{\theta}=3\)
(4)
\(\tan{\theta}=1\)
Check Answer
Option 3
Q.No:5 CSIR June-2016
A loop of radius \(a\), carrying a current \(I\), is placed in a uniform magnetic field \(\mathbf{B}\). If the normal to the loop is denoted by \(\hat{n}\), the force \(\mathbf{F}\) and the torque \(\mathbf{T}\) on the loop are
(1)
\(\mathbf{F}=0\) and \(\mathbf{T}=\pi a^2 I \hat{n}\times \mathbf{B}\)
(2)
\(\mathbf{F}=\frac{\mu_0}{4\pi} \mathbf{I}\times \mathbf{B}\) and \(\mathbf{T}=0\)
(3)
\(\mathbf{F}=\frac{\mu_0}{4\pi} \mathbf{I}\times \mathbf{B}\) and \(\mathbf{T}=I \hat{n}\times \mathbf{B}\)
(4)
\(\mathbf{F}=0\) and \(\mathbf{T}=\frac{1}{\mu_0 \varepsilon_0} I \mathbf{B}\)
Check Answer
Option 1
Q.No:6 CSIR June-2017
A set of \(N\) concentric circular loops of wire, each carrying a steady current \(I\) in the same direction, is arranged in a plane. The radius of the first loop is \(r_1=a\) and the radius of the \(n^{\text{th}}\) loop is given by \(r_n=nr_{n-1}\). The magnitude \(B\) of the magnetic field at the centre circles in the limit \(N\to \infty\), is
(1)
\(\mu_0 I(e^2-1)/4\pi a\)
(2)
\(\mu_0 I(e-1)/\pi a\)
(3)
\(\mu_0 I(e^2-1)/8a\)
(4)
\(\mu_0 I(e-1)/2a\)
Check Answer
Option 4
Q.No:7 CSIR June-2017
A constant current \(I\) is flowing in a piece of wire that is bent into a loop as shown in the figure.

The magnitude of the magnetic field at the point \(O\) is
(1)
\(\frac{\mu_0 I}{4\pi \sqrt{5}}\ln{\left(\frac{a}{b}\right)}\)
(2)
\(\frac{\mu_0 I}{4\pi \sqrt{5}}\left(\frac{1}{a}-\frac{1}{b}\right)\)
(3)
\(\frac{\mu_0 I}{4\pi \sqrt{5}}\left(\frac{1}{a}\right)\)
(4)
\(\frac{\mu_0 I}{4\pi \sqrt{5}}\left(\frac{1}{b}\right)\)
Check Answer
Option 2
Q.No:8 CSIR Dec-2017
A circular current carrying loop of radius \(a\) carries a steady current. A constant electric charge is kept at the centre of the loop. The electric and magnetic fields, \(\vec{E}\) and \(\vec{B}\) respectively, at a distance \(d\) vertically above the centre of the loop satisfy
(1)
\(\vec{E}\perp \vec{B}\)
(2)
\(\vec{E}=0\)
(3)
\(\vec{\nabla}(\vec{E}\cdot \vec{B})=0\)
(4)
\(\vec{\nabla}\cdot(\vec{E}\times \vec{B})=0\)
Check Answer
Option 4
Q.No:9 CSIR June-2018
The loop shown in the figure below carries a steady current \(I\).

The magnitude of the magnetic field at the point \(O\) is
(1)
\(\frac{\mu_0 I}{2a}\)
(2)
\(\frac{\mu_0 I}{6a}\)
(3)
\(\frac{\mu_0 I}{4a}\)
(4)
\(\frac{\mu_0 I}{3a}\)
Check Answer
Option 2
Q.No:10 CSIR Dec-2018
Two current-carrying circular loops, each of radius \(R\), are placed perpendicular to each other, as shown in the figure below.

The loop in the \(xy\)-plane carries a current \(I_0\) while that in the \(xz\)-plane carries a current \(2I_0\). The resulting magnetic field \(\vec{B}\) at the origin is
(1)
\(\frac{\mu_0 I_0}{2R}[2\hat{j}+\hat{k}]\)
(2)
\(\frac{\mu_0 I_0}{2R}[2\hat{j}-\hat{k}]\)
(3)
\(\frac{\mu_0 I_0}{2R}[-2\hat{j}+\hat{k}]\)
(4)
\(\frac{\mu_0 I_0}{2R}[-2\hat{j}-\hat{k}]\)
Check Answer
Option 3
Q.No:11 CSIR Dec-2018
A rotating spherical shell of uniform surface charge and mass density has total mass \(M\) and charge \(Q\). If its angular momentum is \(L\) and magnetic moment is \(\mu\), then the ratio \(\mu/L\) is
(1)
\(\frac{Q}{3M}\)
(2)
\(\frac{2Q}{3M}\)
(3)
\(\frac{Q}{2M}\)
(4)
\(\frac{3Q}{4M}\)
Check Answer
Option 3
Q.No:12 CSIR June-2019
Consider a planar wire loop as an \(n\)-sided regular polygon, in which \(R\) is the distance from the centre to a vertex. If a steady current \(I\) flows through the wire, the magnitude of the magnetic field at the centre of the loop is
(1)
\(\frac{\mu_0 I}{2R} \sin{\left(\frac{2\pi}{n}\right)}\)
(2)
\(\frac{\mu_0 nI}{4\pi R} \sin{\left(\frac{\pi}{n}\right)}\)
(3)
\(\frac{\mu_0 nI}{2\pi R} \tan{\left(\frac{2\pi}{n}\right)}\)
(4)
\(\frac{\mu_0 nI}{2\pi R} \tan{\left(\frac{\pi}{n}\right)}\)
Check Answer
Option 4
Q.No:13 CSIR June-2019
Which of the following is \({\bf not}\) a correct boundary condition at an interface between two homogeneous dielectric media? (In the following \(\hat{n}\) is a unit vector normal to the interface, \(\sigma\) and \(\mathbf{j}_s\) are the surface charge and current densities, respectively.)
(1)
\(\hat{n}\times (\mathbf{D}_1-\mathbf{D}_2)=0\)
(2)
\(\hat{n}\times (\mathbf{H}_1-\mathbf{H}_2)=\mathbf{j}_s\)
(3)
\(\hat{n}\cdot (\mathbf{D}_1-\mathbf{D}_2)=\sigma\)
(4)
\(\hat{n}\cdot (\mathbf{B}_1-\mathbf{B}_2)=0\)\)
Check Answer
Option 1
Q.No:14 CSIR Dec-2019
A positively charged particle is placed at the origin (with zero initial velocity) in the presence of a constant electric and a constant magnetic field along the positive \(z\) and \(x\) directions, respectively. At large times, the overall motion of the particle is adrift along the
(1)
positive \(y\)-direction
(2)
negative \(z\)-direction
(3)
positive \(z\)-direction
(4)
negative \(y\)-direction
Check Answer
Option 1
Q.No:15 Assam CSIR Dec-2019
A charged particle, starting from rest, is accelerated to a speed \(v\) in a uniform electric field \(\vec{E}=E\hat{i}\) for a distance \(L\). The particle is then injected in a region with a uniform magnetic field \(\vec{B}=B\hat{k}\) and no electric field, so that it moves in a circular trajectory of radius \(R\). The speed \(v\) of the particle may be expressed as
(1)
\(\frac{RE}{2LB}\)
(2)
\(\frac{2LE}{RB}\)
(3)
\(\frac{LE}{2RB}\)
(4)
\(\frac{2RE}{LB}\)
Check Answer
Option 2
Q.No:16 CSIR June-2020
Three infinitely long wires, each carrying equal current are placed in the \(xy\)-plane along \(x=0, +d\) and \(-d\). On the \(xy\)-plane, the magnetic field vanishes at
(a)
\(x=\pm \frac{d}{2}\)
(b)
\(x=\pm d\left(1+\frac{1}{\sqrt{3}}\right)\)
(c)
\(x=\pm d\left(1-\frac{1}{\sqrt{3}}\right)\)
(d)
\(x=\pm \frac{d}{\sqrt{3}}\)
Check Answer
Option d
Q.No:17 CSIR Feb-2022
In an experiment to measure the charge to mass ratio e m/ of the electron by Thomson's
method, the values of the deflecting electric field and the accelerating potential are \(6\times 10^6 N/C\)
(newton per coulomb) and \(150V\) , respectively. The magnitude of the magnetic field that leads to
zero deflection of the electron beam is closest to
(1)
\(0.6\) T
(2)
\(1.2\) T
(3)
\(0.4\) T
(4)
\(0.8\) T
Check Answer
Option 4
Q.No:18 CSIR Feb-2022
The vector potential for an almost point like magnetic dipole located at the origin is \(\vec{A}=\frac{\mu sin\theta}{4\pi r^2}\hat{\phi}\) where \((r,\theta,\phi)\) denote the spherical polar coordinates and \(\hat{\phi}\) is the unit vector
along \(\hat{\phi}\) . A particle of mass m and charge \(q\) , moving in the equatorial plane of the
dipole, starts at time= \(t=0\) with an initial speed\(v_0\) and an impact parameter \(b\) . Its
instantaneous speed at the point of closest approach is
(1)
\(v_0\)
(2)
\(0/0\)
(3)
\(v_0+\frac{\mu q}{4\pi mb^2}\)
(4)
\(\sqrt{v_0^2+(\frac{\mu q}{4\pi mb^2})^2}\)
Check Answer
Option 1
Q.No:19 CSIR Sep-2022
A part of an infinitely long wire, carrying a current \(I\), is bent in a semi-circular arc of radius \(r\) (as shown in the figure).

The magnetic field at the centre \(O\) of the arc is
(1)
\(\frac{\mu_0 I}{4r}\)
(2)
\(\frac{\mu_0 I}{4\pi r}\)
(3)
\(\frac{\mu_0 I}{2r}\)
(4)
\(\frac{\mu_0 I}{2\pi r}\)
Check Answer
Option 1
Q.No:20 CSIR Sep-2022
Two parallel conducting rings, both of radius \(R\), are separated by a distance \(R\). The planes of the rings are perpendicular to the line joining their centers, which is taken to be \(x\)-axis.

If both the rings carry the same current \(i\) along the same direction, the magnitude of the magnetic field along \(x-\)axis is best represented by

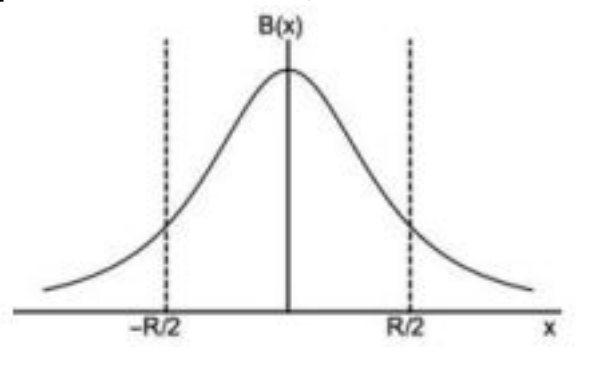


Check Answer
Option 1
Q.No:21 CSIR Sep-2022
A stationary magnetic dipole \(\textbf{m}=m\hat{k}\) is placed above an infinite surface (\(z=0\)) carrying uniform surface current density \(\vec{\kappa}\)=\(\kappa\hat{i}\).
The torque on the dipole is
(1)
\(\frac{\mu_0}{2} m \kappa \hat{i} \)
(2)
\(-\frac{\mu_0}{2} m \kappa\hat{i} \)
(3)
\(\frac{\mu_0}{2} m \kappa \hat{j}\)
(4)
\(-\frac{\mu_0}{2} m \kappa \hat{j}\)
Check Answer
Option 1
Q.No:21 CSIR Dec-2023
A small bar magnet is placed in a magnetic field \(\mathbf{B}(\mathbf{r}) = B(x) \hat{z}\). The magnet is initially at rest with its magnetic moment along \(\hat{y}\). At later times, it will undergo
1) angular motion in the yz plane and translational motion along \(\hat{y}\)
2) angular motion in the yz plane and translational motion along \(\hat{x}\)
3) angular motion in the zx plane and translational motion along \(\hat{z}\)
4) angular motion in the xy plane and translational motion along \(\hat{z}\)
Check Answer
Option 2
Q.No:22 CSIR June-2024
A particle of unit mass and unit charge is moving in a magnetic field, which varies as \(\mathbf{B}(\mathbf{r}) = b_0 \mathbf{r}/r^3\) (\(b_0\) is a constant) over a region far away from the origin. If \(\mathbf{L}\) is the instantaneous angular momentum of the particle within that region, then \(\frac{d\mathbf{L}}{dt}\) is
1) \( 2b_0 \frac{d}{dt} \left(\frac{\mathbf{r}}{r}\right) \)
2) \( -b_0 \frac{d}{dt} \left(\frac{\mathbf{r}}{r}\right) \)
3) \( b_0 \frac{d}{dt} \left(\frac{\mathbf{r}}{r}\right) \)
4) \( 0 \)
Check Answer
Option 3
Q.No:23 CSIR Dec-2024
A sphere with uniform charge and mass density, having total charge \(Q\) and mass \(M\), rotates about an axis through its center with angular velocity \(\omega\). The ratio of its magnetic dipole moment to its angular momentum is
1) \(\frac{2Q}{M}\)
2) \(\frac{Q}{M}\)
3) \(\frac{Q}{2M}\)
4) \(\frac{Q}{4M}\)
Check Answer
Option 3
Q.No:24 CSIR Dec-2024
An electron enters a region of uniform electric and magnetic fields \(\vec{E}_{0}\) and \(\vec{B}_{0}\). Its velocity, \(\vec{v}\), \(\vec{E}_{0}\), and \(\vec{B}_{0}\) are mutually perpendicular to each other. Initially, \(E_{0}\) is so adjusted that the electron suffers no deflection. \(E_{0}\) is then switched off and the electron moves in a circular path of radius \(R\). The speed of the electron and its charge to mass ratio would be
1) \(\frac{2E_{0}}{B_{0}},\; \frac{E_{0}}{2B_{0}^{2}R}\)
2) \(\frac{2E_{0}}{B_{0}},\; \frac{E_{0}}{B_{0}^{2}R}\)
3) \(\frac{E_{0}}{B_{0}},\; \frac{E_{0}}{B_{0}^{2}R}\)
4) \(\frac{E_{0}}{B_{0}},\; \frac{2E_{0}}{B_{0}^{2}R}\)
Check Answer
Option 3
Q.No:25 CSIR June-2025
A circular loop of radius \(a\) (in the \(x\!-\!y\) plane) and a square loop of side \(b\) (in the \(x\!-\!z\) plane) are kept at a distance \(r\). Both carry current \(I\) as shown in the figure. If \(r \gg a,b\), the torque exerted on the square loop by the circular loop is
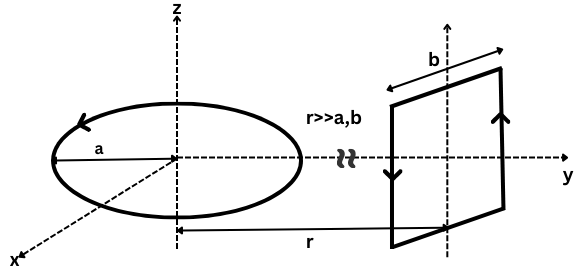
1) \(-\frac{\mu_{0}}{4\pi}\frac{1}{r^{3}}\pi a^{2} b^{2} I^{2}\,\hat{z}\)
2) \(0\)
3) \(\frac{\mu_{0}}{4\pi}\frac{1}{r^{3}}\pi a^{2} b^{2} I^{2}\,\hat{x}\)
4) \(-\frac{\mu_{0}}{4\pi}\frac{1}{r^{3}}\pi a^{2} b^{2} I^{2}\,\hat{x}\)
Check Answer
Option 4
Q.No:26 CSIR June-2025
Two identical cubes are shown in figures (a) and (b). The magnitude of the magnetic field at the centre of the cube in (a), produced by the currents as shown, is \(B_{0}\). The magnitude of the magnetic field at the centre of the cube in (b) will be


1) \(\sqrt{3}\,B_{0}\)
2) \(2\,B_{0}\)
3) \(\frac{3}{2}\,B_{0}\)
4) \(\sqrt{2}\,B_{0}\)
Check Answer
Option 1
Q.No:27 CSIR June-2025
A long cylinder of radius \(R\) carries a magnetization \(\vec{M} = k\rho^{2}\hat{\phi}\), where \(k\) is a constant, \(\rho\) is the radial distance from the axis and \(\hat{\phi}\) is the azimuthal unit vector. The magnetic field inside and outside the cylinder would be
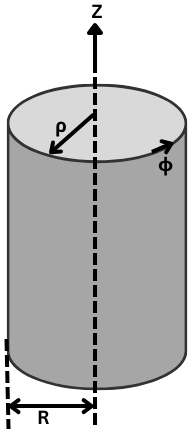
1) \(\vec{B}_{\text{inside}} = 0,\quad \vec{B}_{\text{outside}} = \mu_{0}k\rho^{2}\hat{\phi}\)
2) \(\vec{B}_{\text{inside}} = \mu_{0}k\rho^{2}\hat{\phi},\quad \vec{B}_{\text{outside}} = 0\)
3) \(\vec{B}_{\text{inside}} = \vec{B}_{\text{outside}} = \mu_{0}k\rho^{2}\hat{\phi}\)
4) \(\vec{B}_{\text{inside}} = \vec{B}_{\text{outside}} = 0\)
