Q.No:1 JAM-2015
A positively charged particle, with a charge \(q\), enters a region in which there is a uniform electric field \(\vec{E}\) and a uniform magnetic field \(\vec{B}\), both directed parallel to the positive y- axis. At \(t=0\) the particle is at the origin and has a speed \(v_0\) directed along the positive x- axis. The orbit of the particle, projected on the x-z plane, is a circle. Let ܶ be the time taken to complete one revolution of this circle. The y-coordinate of the particle at \(t=T\) given by
(A)
\(\frac{\pi^2 m E}{2qB^2}\)
(B)
\(\frac{2\pi^2 m E}{qB^2}\)
(C)
\(\frac{\pi^2 m E}{qB^2}+\frac{v_0 \pi m}{qB}\)
(D)
\(\frac{2\pi m v_0}{qB}\)
Check Answer
Option B
Q.No:2 JAM-2015
A conducting wire is in the shape of a regular hexagon, which is inscribed inside an imaginary circle of radius \(R,\) as shown. A current \(I\) flows through the wire. The magnitude of the magnetic field at the center of the circle is
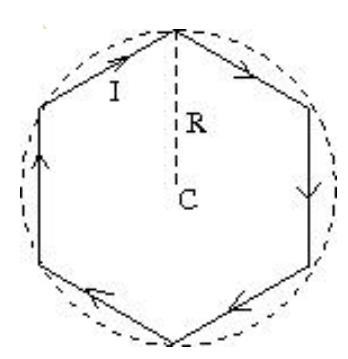
(A)
\(\frac{\sqrt{3}\mu_0 I}{2\pi R}\)
(B)
\(\frac{\mu_0 I}{2\sqrt{3}\pi R}\)
(C)
\(\frac{\sqrt{3}\mu_0 I}{\pi R}\)
(D)
\(\frac{3\mu_0 I}{2\pi R}\)
Check Answer
Option C
Q.No:3 JAM-2016
A charged particle in a uniform magnetic field \(\vec{B}=B_0\hat{e}_z\) starts moving from the origin with
velocity \(\vec{v}=(3\hat{e}_x+2\hat{e}_z)\)m/s. The trajectory of the particle and the time \(t\) which it reaches 2 meters above the xy- plane are
\((\hat{e}_x, \hat{e}_y\) and \(\hat{e}_y\) are unit vectors in Cartesian−coordinate system.)
(A)
Helical path ; \(t=1\) s.
(B)
Helical path ; \(t=2/3\) s.
(C)
Circular path ; \(t=1\) s.
(D)
Circular path ; \(t=2/3\) s.
Check Answer
Option A
Q.No:4 JAM-2016
Three infinitely-long conductors carrying currents \(l_1,l_2\) and \(l_3\) lie perpendicular to the plane of the paper as shown below.

If the value of the integral \(\oint_C \vec{B} \cdot \vec{dl}\) for the loops \(C_1,C_2\) and \(C_3\) are \(2\mu_0,4\mu_0\) and \(\mu_0\) in the units of
N/A, respectively, then
(A)
\(I_1=3\)A into the paper.
(B)
\(I_2=5\)A out of the paper.
(C)
\(I_3=0\).
(D)
\(I_3=1\)A out of the paper.
Check Answer
Option A,B
Q.No:5 JAM-2017
A current \(I=10A\) flows in an infinitely long wire along the axis of hemisphere (see figure). The value of \(\int (\vec{\nabla}\times \vec{B}) \cdot \vec{ds}\) over the hemispherical surface as shown in the figure is:
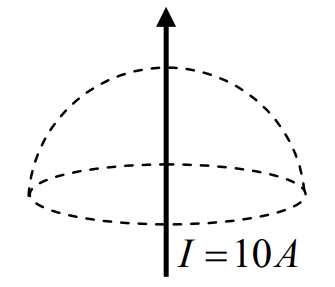
(A)
\(10\mu_0\)
(B)
\(5\mu_0\)
(C)
\(0\)
(D)
\(7.5\mu_0\)
Check Answer
Option A
Q.No:6 JAM-2017
Consider a thin long insulator coated conducting wire carrying current \(I\) . It is now wound once around an insulating thin disc of radius \(R\) to bring the wire back on the same side, as shown in the figure. The magnetic field at the centre of the disc is equal to:
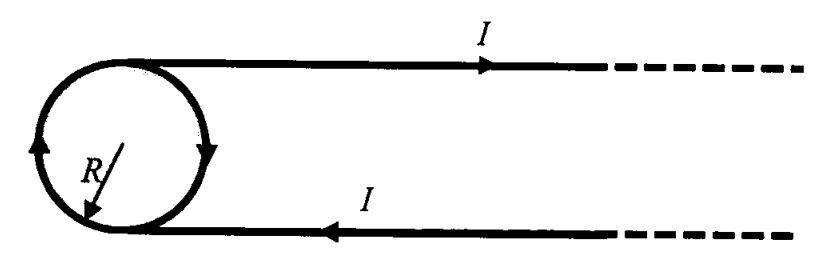
(A)
\([\frac{\mu_0 I}{2R}]\)
(B)
\(\frac{\mu_0 I}{4R}[3+\frac{2}{\pi}]\)
(C)
\(\frac{\mu_0 I}{4R}[1+\frac{2}{\pi}]\)
(D)
\(\frac{\mu_0 I}{2R}[1+\frac{1}{\pi}]\)
Check Answer
Option B
Q.No:7 JAM-2018
A current \(I\) is flowing through the sides of an equilateral triangle of side \(a\). The magnitude of the magnetic field at the centroid of the triangle is
(A)
\(\frac{9\mu_0 I}{2\pi a}\)
(B)
\(\frac{\mu_0 I}{\pi a}\)
(C)
\(\frac{3\mu_0 I}{2\pi a}\)
(D)
\(\frac{3\mu_0 I}{\pi a}\)
Check Answer
Option A
Q.No:8 JAM-2018
In presence of a magnetic field \(B\hat{j}\) and an electric field \((-E)\hat{k}\), a particle moves undeflected.
Which of the following statements is (are) correct?
(A)
The particle has positive charge, velocity =\(-\frac{E}{B}\hat{i}\)
(B)
The particle has positive charge, velocity =\(\frac{E}{B}\hat{i}\)
(C)
The particle has negative charge, velocity =\(-\frac{E}{B}\hat{i}\)
(D)
The particle has negative charge, velocity =\(\frac{E}{B}\hat{i}\)
Check Answer
Option B,D
Q.No:9 JAM-2019
Which one of the following is an impossible magnetic field \(\vec{B}\) ?
(A)
\(\vec{B}=3x^2z^2\hat{x}-2xz^3\hat{z}\)
(B)
\(\vec{B}=-2xy\hat{x}+yz^2\hat{y}+(2zy-\frac{z^3}{3})\hat{z}\)
(C)
\(\vec{B}=(x+4y)\hat{x}-yx^3\hat{y}+(x^3z-\frac{z^2}{2})\hat{z}\)
(D)
\(\vec{B}=-6xz\hat{x}+3yz^2\hat{y}\)
Check Answer
Option D
Q.No:10 JAM-2019
A surface current \(\vec{K}=100\hspace{0.5mm} \hat{x} A/m\) flows on the surface \(z=0\), which separates two media with magnetic permeabilities \(\mu_1\) and \(\mu_2\) as shown in the figure. If the magnetic field in the region 1 is \(\vec{B}_1=4\hat{x}-6\hat{y}+2\hat{z}\hspace{0.5mm}\) mT, then the magnitude of the normal component of \(\vec{B}_2\) will be ___________________ mT.
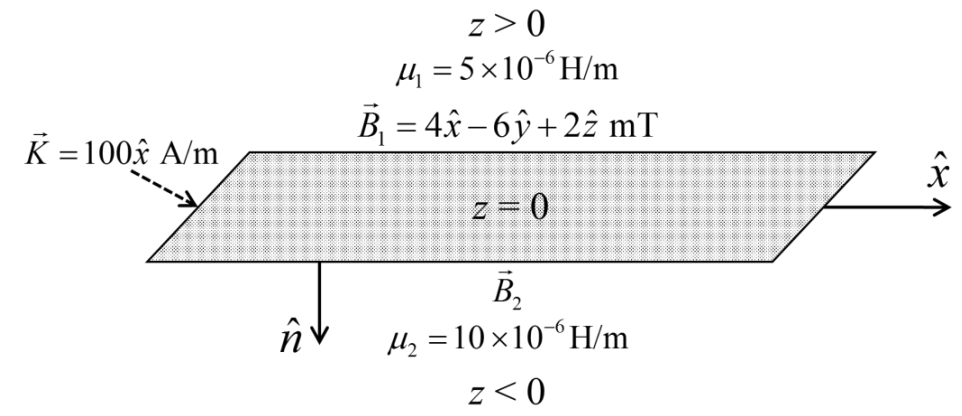
Check Answer
Ans 2
Q.No:11 JAM-2020
Consider an annular region in free space containing a uniform magnetic field in the z-direction, schematically represented by the shaded region in the figure. A particle having charge \(Q\) and mass \(M\) starts off from point \(P (a , 0, 0)\) in the +x-direction with constant speed \(v\). If the radii of inner and outer circles are \(a\) and \(b\), respectively, the minimum magnetic field required so that the particle
returns to the inner circle is
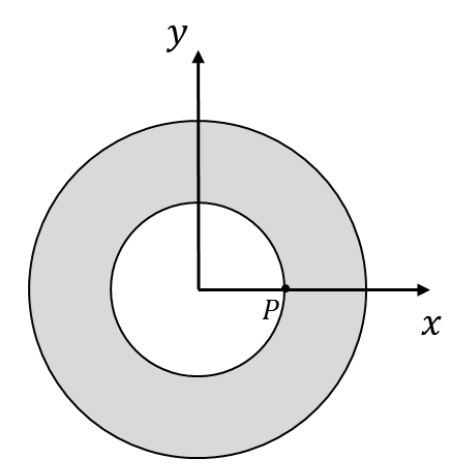
(A)
\(\frac{M v}{Q}(\frac{b^2-a^2}{b})^{-1}\)
(B)
\(\frac{M v}{Q}(\frac{b^2-a^2}{2b})^{-1}\)
(C)
\(\frac{M v}{Q}(\frac{b^2-a^2}{3b})^{-1}\)
(D)
\(\frac{M v}{Q}(\frac{b^2-a^2}{4b})^{-1}\)
Check Answer
Option B
Q.No:12 JAM-2020
The magnetic fields in tesla in the two regions separated by the \(z=0\) plane are given by \(\vec{B}_1=3\hat{x}+5\hat{z}\) and \(\vec{B}_2=\hat{x}+3\hat{y}+5\hat{z}\). The magnitude of the surface current density at the interface between the two regions is \(\alpha \times 10^6\) A/m. Given the permeability of the free space \(\mu_o=4\pi \times 10^{-7} N/A^2\), the value of \(\alpha\) is _____________________ . (Round off to 2 decimal places)
Check Answer
Ans 2.86-2.88
Q.No:13 JAM-2021
A current \(I\) is uniformly distributed across a long straight nonmagnetic wire \((\mu_r =1 )\) of circular cross-section with radius \(a\). Two points P and Q are at distances \(\frac{a}{3}\) and \(9a\), respectively, from the axis of the wire. The ratio of the magnetic fields at points P and Q is _____________.
Check Answer
Ans 3
Q.No:14 JAM-2022
Consider a conical region of height \(h\) and base radius \(R\) with its vertex at the origin. Let the outward normal to its base be along the positive z-axis, as shown in the figure. A uniform magnetic field, \(\vec{B}=B_0 \hat{z}\) exists everywhere. Then the magnetic flux through the base \((\Phi_b)\) and that through the curved surface of the
cone \((\Phi_c)\) are

(A)
\(\Phi_b= B_0 \pi R^2 \) ; \(\Phi_c= 0 \)
(B)
\(\Phi_b= \frac{1}{2}B_0 \pi R^2 \) ; \(\Phi_c= \frac{1}{2}B_0 \pi R^2\)
(C)
\(\Phi_b= 0 \) ; \(\Phi_c= -B_0 \pi R^2 \)
(D)
\(\Phi_b= B_0 \pi R^2 \) ; \(\Phi_c= -B_0 \pi R^2 \)
Check Answer
Option D
Q.No:15 JAM-2022
Consider a thin annular sheet, lying on the xy-plane, with \(R_1\) and \(R_2\) as its inner and outer radii, respectively. If the sheet carries a uniform surface-charge density \(\sigma\) and spins about the origin \(O\) with a constant angular velocity \(\bar{\omega}=\omega_0 \hat{z}\),then, the total current flow on the sheet is

(A)
\(\frac{2\pi \sigma \omega_0(R_2 ^3 -R_1 ^3)}{3}\)
(B)
\(\sigma \omega_0(R_2 ^3 -R_1 ^3)\)
(C)
\(\frac{\pi \sigma \omega_0(R_2 ^3 -R_1 ^3)}{3}\)
(D)
\(\frac{2\pi \sigma \omega_0(R_2 -R_1 )^3}{3}\)
Check Answer
Option MTA
Q.No:16 JAM-2022
A uniform magnetic field \(\vec{B}=B_0 \hat{z}\), where \(B_0>0\) exists as shown in the figure. A charged particle of mass \(m\) and charge \(q(q>0)\) is released at the origin, in the yz-plane, with a velocity \(\vec{v}\) directed at an angle \(\theta = 45^\circ \) with respect to the positive z-axis. Ignoring gravity, which one of the following is \(\textbf{TRUE.}\)
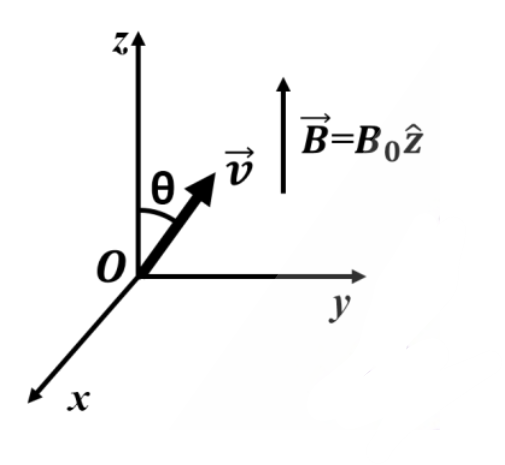
(A)
The initial acceleration \(\vec{a}=\frac{qvB_0}{\sqrt{2}m}\hat{x}\)
(B)
The initial acceleration \(\vec{a}=\frac{qvB_0}{\sqrt{2}m}\hat{y}\)
(C)
The particle moves in a circular path
(D)
The particle continues in a straight line with constant speed
Check Answer
Option A
Q.No:17 JAM-2025
A surface current density
\[
\vec{K}(y) = a e^{-y}
\]
exists on a thin strip of width \(b\), as shown in the figure.
The associated surface current is ______.
(\(a\) is a constant of appropriate dimensions)

A) \(a(1 - e^{-b})\)
B) \(a(1 + e^{-b})\)
C) \(a(e^{-b} - 1)\)
D) \(a(e^{b} + e^{-b})\)
Check Answer
Option A
Q.No:18 JAM-2025
A magnetic field is given by
\[
\vec{B} = \nabla \times \vec{A}
\]
where \(\vec{A}\) is the magnetic vector potential.
If
\[
\vec{A} = (a x^2 + b y^2)\,\hat{i},
\]
the corresponding current density \(\vec{J}\) is ______.
(\(a\) and \(b\) are non-zero constants)
A) \(-\frac{1}{\mu_0}(2a + 2b)\hat{i}\)
B) \(\frac{1}{\mu_0}(2a + 2b)\hat{i}\)
C) \(-\frac{1}{\mu_0}(2a)\hat{i}\)
D) \(-\frac{1}{\mu_0}(2b)\hat{i}\)
