Q.No:1 CSIR Dec-2014
The function \(f(x)=\sum_{n=0}^{\infty} \frac{(-1)^n}{n!(n+1)!} \left(\frac{x}{2}\right)^{2n+1}\) satisfies the differential equation
(1)
\(x^2 \frac{d^2 f}{dx^2}+x \frac{df}{dx}+(x^2+1)f=0\)
(2)
\(x^2 \frac{d^2 f}{dx^2}+2x \frac{df}{dx}+(x^2-1)f=0\)
(3)
\(x^2 \frac{d^2 f}{dx^2}+x \frac{df}{dx}+(x^2-1)f=0\)
(4)
\(x^2 \frac{d^2 f}{dx^2}-x \frac{df}{dx}+(x^2-1)f=0\)
Check Answer
Option 3
Q.No:2 CSIR June-2015
Consider the differential equation \(\frac{d^2 x}{dt^2} - 3 \frac{dx}{dt} + 2x = 0\). If x = 0 at t = 0 and x = 1 at t = 1, the value of x at t = 2 is
(1)
\(e^2+1\)
(2)
\(e^2 +e\)
(3)
\(e+2\)
(4)
2e
Check Answer
Option 2
Q.No:3 CSIR June-2015
Let \(f(x, t)\) be a solution of the wave equation are \(\frac{\partial^2 f}{\partial t^2} = v^{2} \frac{\partial^2 f}{\partial t^2}\) 1-dimension. If at \(t = 0, f (x,0) = e^{-x^2}\) and \(\frac{\partial f}{\partial t}(x,0) = 0\) for all x, then \(f(x, t)\) for all future times \(t > 0\) is described by
(1)
\(e-(x^2-v^{2}t^{2})\)
(2)
\(e^{-(x-vt)^{2}}\)
(3)
\(\frac{1}{4} e^{-(x - vt)^{2}} + \frac{3}{4} e^{-(x + vt)^{2}}\)
(4)
\(\frac{1}{2} [e^{-(x - vt)^{2}} + e^{-(x + vt)^{2}}]\)
Check Answer
Option 4
Q.No:4 CSIR Dec-2015
If \(y=\frac{1}{\tanh{(x)}}\), then \(x\) is
(1)
\(\ln{\left(\frac{y+1}{y-1}\right)}\)
(2)
\(\ln{\left(\frac{y-1}{y+1}\right)}\)
(3)
\(\ln{\sqrt{\frac{y-1}{y+1}}}\)
(4)
\(\ln{\sqrt{\frac{y+1}{y-1}}}\)
Check Answer
Option 4
Q.No:5 CSIR Dec-2015
The solution of the differential equation \(\frac{dx}{dt}=2\sqrt{1-x^2}\), with initial condition \(x=0\) at \(t=0\) is
(1)
\(x=\left\{\begin{array}{cc}\sin{2t}, & 0\leq t< \frac{\pi}{4}\\ \sinh{2t}, & t\geq \frac{\pi}{4}\end{array}\right.\)
(2)
\(x=\left\{\begin{array}{cc}\sin{2t}, & 0\leq t< \frac{\pi}{2}\\ 1, & t\geq \frac{\pi}{2}\end{array}\right.\)
(3)
\(x=\left\{\begin{array}{cc}\sin{2t}, & 0\leq t< \frac{\pi}{4}\\ 1, & t\geq \frac{\pi}{4}\end{array}\right.\)
(4)
\(x=1-\cos{2t}, t\geq 0\)
Check Answer
Option 3
Q.No:6 CSIR Dec-2015
The Hermite polynomial \(H_n(x)\) satisfies the differential equation
\[
\frac{d^2 H_n}{dx^2}-2x\frac{dH_n}{dx}+2nH_n(x)=0.
\]
The corresponding generating function \(G(t, x)=\sum_{n=0}^{\infty} \frac{1}{n!} H_n(x)t^n\) satisfies the equation
(1)
\(\frac{\partial^2 G}{\partial x^2}-2x\frac{\partial G}{\partial x}+2t\frac{\partial G}{\partial t}=0\)
(2)
\(\frac{\partial^2 G}{\partial x^2}-2x\frac{\partial G}{\partial x}-2t^2\frac{\partial G}{\partial t}=0\)
(3)
\(\frac{\partial^2 G}{\partial x^2}-2x\frac{\partial G}{\partial x}+2\frac{\partial G}{\partial t}=0\)
(4)
\(\frac{\partial^2 G}{\partial x^2}-2x\frac{\partial G}{\partial x}+2\frac{\partial^2 G}{\partial x \partial t}=0\)
Check Answer
Option 1
Q.No:7 CSIR Dec-2015
For a dynamical system governed by the equation \(\frac{dx}{dt}=2\sqrt{1-x^2}\), with \(|x|\leq 1\),
(1)
\(x=-1\) and \(x=1\) are both unstable fixed points
(2)
\(x=-1\) and \(x=1\) are both stable fixed points
(3)
\(x=-1\) is an unstable fixed point and \(x=1\) is a stable fixed point
(4)
\(x=-1\) is a stable fixed point and \(x=1\) is an unstable fixed point
Check Answer
Option 3
Q.No:8 CSIR June-2016
The integral equation \(\phi(x, t)=\lambda \int dx' dt' \int \frac{d\omega dk}{(2\pi)^2} \frac{e^{-ik(x-x')+i\omega(t-t')}}{\omega^2-k^2-m^2+i\epsilon} \phi^3(x', t')\) is equivalent to the differential equation
(1)
\(\left(\frac{\partial^2}{\partial t^2}+\frac{\partial^2}{\partial x^2}-m^2+i\epsilon\right)\phi(x, t)=-\frac{1}{6} \lambda \phi^3(x, t)\)
(2)
\(\left(\frac{\partial^2}{\partial t^2}-\frac{\partial^2}{\partial x^2}+m^2-i\epsilon\right)\phi(x, t)=\lambda \phi^2(x, t)\)
(3)
\(\left(\frac{\partial^2}{\partial t^2}-\frac{\partial^2}{\partial x^2}+m^2-i\epsilon\right)\phi(x, t)=-3 \lambda \phi^2(x, t)\)
(4)
\(\left(\frac{\partial^2}{\partial t^2}-\frac{\partial^2}{\partial x^2}+m^2-i\epsilon\right)\phi(x, t)=-\lambda \phi^3(x, t)\)
Check Answer
Option 4
Q.No:9 CSIR June-2016
A radioactive element \(X\) decays to \(Y\), which in turn decays to a stable element \(Z\). The decay constant from \(X\) to \(Y\) is \(\lambda_1\), and that from \(Y\) to \(Z\) is \(\lambda_2\). If, to begin with, there are only \(N_0\) atoms of \(X\), at {\bf short} times (\(t\ll 1/\lambda_1\) as well as \(1/\lambda_2\)) the number of atoms of \(Z\) will be
(1)
\(\frac{1}{2}\lambda_1 \lambda_2 N_0 t^2\)
(2)
\(\frac{\lambda_1 \lambda_2}{2(\lambda_1+\lambda_2)} N_0 t\)
(3)
\((\lambda_1+\lambda_2)^2 N_0 t^2\)
(4)
\((\lambda_1+\lambda_2) N_0 t\)
Check Answer
Option 1
Q.No:10 CSIR Dec-2016
Consider two radioactive atoms, each of which has a decay rate of \(1\) per year. The probability that at least one of them decays in the first two years is
(1)
\(\frac{1}{4}\)
(2)
\(\frac{3}{4}\)
(3)
\(1-e^{-4}\)
(4)
\((1-e^{-2})^2\)
Check Answer
Option 3
Q.No:11 CSIR Dec-2016
A ball of mass \(m\) is dropped from a tall building with zero initial velocity. In addition to gravity, the ball experiences a damping force of the form \(-\gamma v\), where \(v\) is its instantaneous velocity and \(\gamma\) is a constant. Given the values \(m=10 kg, \gamma=10 kg/s\), and \(g\approx 10 m/s^2\), the distance travelled (in metres) in time \(t\) in seconds, is
(1)
\(10(t+1-e^{-t})\)
(2)
\(10(t-1+e^{-t})\)
(3)
\(5t^2-(1-e^t)\)
(4)
\(5t^2\)
Check Answer
Option 2
Q.No:12 CSIR Dec-2016
Let \(f(x, t)\) be a solution of the heat equation \(\frac{\partial f}{\partial t}=D \frac{\partial^2 f}{\partial x^2}\) in one dimension. The initial condition at \(t=0\) is \(f(x, 0)=e^{-x^2}\) for \(-\infty< x0\), \(f(x, t)\) is given by [Useful integral: \(\int_{-\infty}^{\infty} dx e^{-\alpha x^2}=\sqrt{\pi/\alpha}\).]
(1)
\(\frac{1}{\sqrt{1+Dt}}e^{-\frac{x^2}{1+Dt}}\)
(2)
\(\frac{1}{\sqrt{1+2Dt}}e^{-\frac{x^2}{1+2Dt}}\)
(3)
\(\frac{1}{\sqrt{1+4Dt}}e^{-\frac{x^2}{1+4Dt}}\)
(4)
\(e^{-\frac{x^2}{1+Dt}}\)
Check Answer
Option 3
Q.No:13 CSIR June-2017
The function \(y(x)\) satisfies the differential equation \(x\frac{dy}{dx}+2y=\frac{\cos{\pi x}}{x}\). If \(y(1)=1\), the value of \(y(2)\) is
(1)
\(\pi\)
(2)
\(1\)
(3)
\(1/2\)
(4)
\(1/4\)
Check Answer
Option 4
Q.No:14 CSIR June-2017
The Green's function satisfying
\[
\frac{d^2}{dx^2} g(x, x_0)=\delta(x-x_0)
\]
with the boundary conditions \(g(-L, x_0)=0=g(L, x_0)\), is
(1)
\(\left\{\begin{array}{ll}\frac{1}{2L}(x_0-L)(x+L), & -L\leq x< x_0 \\ \frac{1}{2L}(x_0+L)(x-L), & x_0\leq x\leq L \end{array}\right.\)
(2)
\(\left\{\begin{array}{ll}\frac{1}{2L}(x_0+L)(x+L), & -L\leq x< x_0 \\ \frac{1}{2L}(x_0-L)(x-L), & x_0\leq x\leq L \end{array}\right.\)
(3)
\(\left\{\begin{array}{ll}\frac{1}{2L}(L-x_0)(x+L), & -L\leq x< x_0 \\ \frac{1}{2L}(x_0+L)(L-x), & x_0\leq x\leq L \end{array}\right.\)
(4)
\(\frac{1}{2L}(x-L)(x+L), -L\leq x\leq L\)
Check Answer
Option 1
Q.No:15 CSIR Dec-2017
The number of linearly independent power series solutions, around \(x=0\), of the second order linear differential equation \(x\frac{d^2 y}{dx^2}+\frac{dy}{dx}+xy=0\), is
(1)
\(0\) (this equation does not have a power series solution)
(2)
\(1\)
(3)
\(2\)
(4)
\(3\)
Check Answer
Option 2
Q.No:16 CSIR Dec-2017
The generating function \(G(t, x)\) for the Legendre polynomials \(P_n(t)\) is
\[
G(t, x)=\frac{1}{\sqrt{1-2xt+x^2}}=\sum_{n=0}^{\infty} x^n P_n(t), \text{ for }|x|<1.
\]
If the function \(f(x)\) is defined by the integral equation \(\int_{0}^{x}f(x')dx'=x G(1, x)\), it can be expressed as
(1)
\(\sum_{n, m=0}^{\infty} x^{n+m} P_n(1) P_m\left(\frac{1}{2}\right)\)
(2)
\(\sum_{n, m=0}^{\infty} x^{n+m} P_n(1) P_m(1)\)
(3)
\(\sum_{n, m=0}^{\infty} x^{n-m} P_n(1) P_m(1)\)
(4)
\(\sum_{n, m=0}^{\infty} x^{n-m} P_n(0) P_m(1)\)
Check Answer
Option 2
Q.No:17 CSIR June-2018
Consider the following ordinary differential equation
\[
\frac{d^2 x}{dt^2}+\frac{1}{x}\left(\frac{dx}{dt}\right)^2-\frac{dx}{dt}=0
\]
with the boundary conditions \(x(t=0)=0\) and \(x(t=1)=1\). The value of \(x(t)\) at \(t=2\) is
(1)
\(\sqrt{e-1}\)
(2)
\(\sqrt{e^2+1}\)
(3)
\(\sqrt{e+1}\)
(4)
\(\sqrt{e^2-1}\)
Check Answer
Option 3
Q.No:18 CSIR June-2018
In the function \(P_n(x)e^{-x^2}\) of a real variable \(x\), \(P_n(x)\) is a polynomial of degree \(n\). The maximum number of extrema that this function can have is
(1)
\(n+2\)
(2)
\(n-1\)
(3)
\(n+1\)
(4)
\(n\)
Check Answer
Option 3
Q.No:19 CSIR June-2018
The Green's function \(G(x, x')\) for the equation \(\frac{d^2 y(x)}{dx^2}+y(x)=f(x)\), with the boundary values \(y(0)=y\left(\frac{\pi}{2}\right)=0\), is
(1)
\(G(x, x')=\left\{\begin{array}{ll}x\left(x'-\frac{\pi}{2}\right), & 0< x< x'< \frac{\pi}{2} \\ \left(x-\frac{\pi}{2}\right)x', & 0< x'< x< \frac{\pi}{2} \end{array}\right.\)
(2)
\(G(x, x')=\left\{\begin{array}{ll}-\cos{x'}\sin{x}, & 0< x< x'< \frac{\pi}{2} \\ -\sin{x'}\cos{x}, & 0< x'< x< \frac{\pi}{2} \end{array}\right.\)
(3)
\(G(x, x')=\left\{\begin{array}{ll}\cos{x'}\sin{x}, & 0< x< x'< \frac{\pi}{2} \\ \sin{x'}\cos{x}, & 0< x'< x< \frac{\pi}{2} \end{array}\right.\)
(4)
\(G(x, x')=\left\{\begin{array}{ll}x\left(\frac{\pi}{2}-x'\right), & 0< x< x'< \frac{\pi}{2} \\ x'\left(\frac{\pi}{2}-x\right), & 0< x'< x< \frac{\pi}{2} \end{array}\right.\)
Check Answer
Option 2
Q.No:20 CSIR Dec-2018
The polynomial \(f(x)=1+5x+3x^2\) is written as a linear combination of the Legendre polynomials (\(P_0(x)=1, P_1(x)=x, P_2(x)=\frac{1}{2}(3x^2-1)\)) as \(f(x)=\sum_n c_n P_n(x)\). The value of \(c_0\) is
(1)
\(1/4\)
(2)
\(1/2\)
(3)
\(2\)
(4)
\(4\)
Check Answer
Option 3
Q.No:21 CSIR Dec-2018
A particle of mass \(m\), moving along the \(x\)-direction, experiences a damping force \(-\gamma v^2\), where \(\gamma\) is a constant and \(v\) is its instantaneous speed. If the speed at \(t=0\) is \(v_0\), the speed at time \(t\) is
(1)
\(v_0 e^{-\frac{\gamma v_0 t}{m}}\)
(2)
\(\frac{v_0}{1+\ln{\left(1+\frac{\gamma v_0 t}{m}\right)}}\)
(3)
\(\frac{mv_0}{m+\gamma v_0 t}\)
(4)
\(\frac{2v_0}{1+e^{\frac{\gamma v_0 t}{m}}}\)
Check Answer
Option 3
Q.No:22 CSIR Dec-2018
In terms of arbitrary constants \(A\) and \(B\), the general solution to the differential equation \(x^2 \frac{d^2 y}{dx^2}+5x\frac{dy}{dx}+3y=0\) is
(1)
\(y=\frac{A}{x}+Bx^3\)
(2)
\(y=Ax+\frac{B}{x^3}\)
(3)
\(y=Ax+Bx^3\)
(4)
\(y=\frac{A}{x}+\frac{B}{x^3}\)
Check Answer
Option 4
Q.No:23 CSIR Dec-2018
The Green's function \(G(x, x')\) for the equation \(\frac{d^2 y(x)}{dx^2}=f(x)\), with the boundary values \(y(0)=0\) and \(y(1)=0\), is
(1)
\(G(x, x')=\left\{\begin{array}{ll}\frac{1}{2}x(1-x'), & 0< x< x'< 1 \\ \frac{1}{2}x'(1-x), & 0< x'< x< 1 \end{array}\right.\)
(2)
\(G(x, x')=\left\{\begin{array}{ll}x(x'-1), & 0< x< x'< 1 \\ x'(1-x), & 0< x'< x< 1 \end{array}\right.\)
(3)
\(G(x, x')=\left\{\begin{array}{ll}-\frac{1}{2}x(1-x'), & 0< x< x'< 1 \\ \frac{1}{2}x'(1-x), & 0< x'< x< 1 \end{array}\right.\)
(4)
\(G(x, x')=\left\{\begin{array}{ll}x(x'-1), & 0< x< x'< 1 \\ x'(x-1), & 0< x'< x< 1 \end{array}\right.\)
Check Answer
Option 4
Q.No:24 CSIR June-2019
The solution of the differential equation \(x\frac{dy}{dx}+(1+x)y=e^{-x}\) with the boundary condition \(y(x=1)=0\), is
(1)
\(\frac{(x-1)}{x}e^{-x}\)
(2)
\(\frac{(x-1)}{x^2}e^{-x}\)
(3)
\(\frac{(1-x)}{x^2}e^{-x}\)
(4)
\((x-1)^2 e^{-x}\)
Check Answer
Option 1
Q.No:25 CSIR June-2019
The time evolution of a coordinate \(x\) of a particle is described by the equation
\[
\frac{d^4 x}{dt^4}+2\Omega^2 \frac{d^2 x}{dt^2}+(\Omega^4-A^4)x=0
\]
For \(\Omega> A\), the particle will
(1)
eventually come to rest at the origin
(2)
eventually drift to infinity (\(|x|\to \infty\))
(3)
oscillate about the origin
(4)
eventually come to rest at \(\Omega/A\) or \(-\Omega/A\)
Check Answer
Option 3
Q.No:26 Assam CSIR Dec-2019
The Green's function \(G(x, x_0)\) for the boundary value problem \(\frac{d^2 y}{dx^2}+2\frac{dy}{dx}=f(x)\) in \(x\geq 0\), with the boundary conditions \(y(0)=\frac{dy}{dx}(0)=0\), is
(1)
\(\left\{\begin{array}{ll}0 & \text{for }0\leq x\leq x_0 \\ \frac{1}{2}(1-e^{2(x_0-x)}) & \text{for }x>x_0 \end{array}\right.\)
(2)
\(\left\{\begin{array}{ll}0 & \text{for }0\leq x\leq x_0 \\ \frac{1}{2}(1-e^{2(x-x_0)}) & \text{for }x>x_0 \end{array}\right.\)
(3)
\(\left\{\begin{array}{ll}\frac{1}{2}(1-e^{2(x-x_0)}) & \text{for }0\leq x\leq x_0 \\ \frac{1}{2}(1-e^{2(x_0-x)}) & \text{for }x>x_0 \end{array}\right.\)
(4)
\(\left\{\begin{array}{ll}\frac{1}{2}(1+e^{2(x-x_0)}) & \text{for }0\leq x\leq x_0 \\ \frac{1}{2}(1-e^{2(x_0-x)}) & \text{for }x>x_0 \end{array}\right.\)
Check Answer
Option 1
Q.No:27 CSIR June-2020
The Green's function for the differential equation \(\frac{d^2 x}{dt^2}+x=f(t)\), satisfying the initial conditions \(x(0)=\frac{dx}{dt}(0)=0\) is
\[
G(t, \tau)=
\left\{
\begin{array}{ll}
0 & \text{for }0<t\tau
\end{array}
\right.
\]
The solution of the differential equation when the source \(f(t)=\theta(t)\) (the Heaviside step function) is
(a)
\(\sin{t}\)
(b)
\(1-\sin{t}\)
(c)
\(1-\cos{t}\)
(d)
\(\cos^2{t}-1\)
Check Answer
Option c
Q.No:28 CSIR June-2020
The solution of the differential equation \(\left(\frac{dy}{dx}\right)^2-\frac{d^2 y}{dx^2}=e^y\), with the boundary conditions \(y(0)=0\) and \(y'(0)=-1\), is
(a)
\(-\ln{\left(\frac{x^2}{2}+x+1\right)}\)
(b)
\(-x\ln{(e+x)}\)
(c)
\(-xe^{-x^2}\)
(d)
\(-x(x+1)e^{-x}\)
Check Answer
Option a
Q.No:29 CSIR Feb-2022
The equation of motion of a one-dimensional forced harmonic oscillator in the presence of
a dissipative force is described by
\(\frac{d^2x}{dt^2}+10\frac{dx}{dt}+16x=6te^{-8t}+4t^2e^{-2t}\) . The general form of the
particular solution, in terms of constants \(A, B\) etc ., is
(1)
\(t(At^2+Bt+C)e^{-2t}+(Dt+E)e^{-8t}\)
(2)
\((At^2+Bt+C)e^{-2t}+(Dt+E)e^{-8t}\)
(3)
\(t(At^2+Bt+C)e^{-2t}+t(Dt+E)e^{-8t}\)
(4)
\((At^2+Bt+C)e^{-2t}+t(Dt+E)e^{-8t}\)
Check Answer
Option 3
Q.No:30 CSIR Feb-2022
The fulcrum of a simple pendulum (consisting of a particle of mass m attached to the
support by a mass less string of length \(l\) oscillates vertically as \(sin(zt)=a \hspace{1mm} sin(\omega t)\), where \(\omega\) is
a constant. The pendulum moves in a vertical plane and \(\theta(t)\) denotes its angular position with
respect to the z -axis

If \(l\frac{d^2\theta}{dt^2}+sin\theta(g-f(t))=0\)(where g is the acceleration due to gravity) describes the
equation of motion of the mass, then \(f(t)\) is
(1)
\(a\omega^2 \hspace{1mm}cos\omega t\)
(2)
\(a\omega^2 \hspace{1mm}sin\omega t\)
(3)
\(-a\omega^2 \hspace{1mm}cos\omega t\)
(4)
\(-a\omega^2 \hspace{1mm}sin\omega t\)
Check Answer
Option
Q.No:31 CSIR Feb-2022
The Legendre polynomials \(P_n(x),n=0,1,2,....\), satisfying the orthogonality condition
\(\int_{-1}^1P_n(x) P_m(x) dx=\frac{2}{2n+1}\delta_{nm}\) on the interval \([-1,+1]\), may be defined by the Rodrigues
formula \(P_n(x)=\frac{1}{2^n n!}\frac{d^n}{dx^n}(x^2-1)^n\). The value of the definite integral \(\int_{-1}^1(4+2x-3x^2+4x^3)P_3(x)dx\) is
(1)
\(3/5\)
(2)
\(11/15\)
(3)
\(23/32\)
(4)
\(16/35\)
Check Answer
Option 4
Q.No:32 CSIR Feb-2022
If we use the Fourier transform \(\phi(x,y)=\int e^{ikx}\phi_k(y)dk\) to solve the partial differential
equation \(-\frac{\partial^2\phi(x,y)}{\partial y^2}-\frac{1}{y^2}\frac{\partial^2\phi(x,y)}{\partial x^2}+\frac{m^2}{y^2}\phi(x,y)=0\) in the half-plane \(\{(x,y):-\infty<x<\infty ,0<y<\infty\}\) , the Fourier modes \(\phi_k(y)\) depend on \(y\) as \(y^\alpha\) and \(y^\beta\) . The value
of \(\alpha\) and \(\beta\) are
(1)
\(\frac{1}{2}+\sqrt{1+4(k^2+m^2)}\) and \(\frac{1}{2}-\sqrt{1+4(k^2+m^2)}\)
(2)
\(1+\sqrt{1+4(k^2+m^2)}\) and \(1-\sqrt{1+4(k^2+m^2)}\)
(3)
\(\frac{1}{2}+\frac{1}{2}\sqrt{1+4(k^2+m^2)}\) and \(\frac{1}{2}-\frac{1}{2}\sqrt{1+4(k^2+m^2)}\)
(4)
\(1+\frac{1}{2}\sqrt{1+4(k^2+m^2)}\) and \(1-\frac{1}{2}\sqrt{1+4(k^2+m^2)}\)
Check Answer
Option 3
Q.No:33 CSIR June-2023
If the Bessel function of integer order \(n\) is defined as \(J_n(x)=\sum_{k=0}^\infty\frac{(-1)^k}{k!(n+k)!}(\frac{x}{2})^{2k+n}\) then \(\frac{d}{dx}[x^{-n} J_n(x)]\) is
1) \(-x^{-(n+1)}J_{n+1}(x)\)
2) \(-x^{-(n+1)}J_{n-1}(x)\)
3) \(-x^{-n}J_{n-1}(x)\)
4) \(-x^{-n}J_{n-1}(x)\)
Check Answer
Option 4
Q.No:34 CSIR June-2023
A layer of ice has formed on a very deep lake. The temperature of water, as well as that of ice at the ice-water interface, are \(0^0C\), whereas the temperature of the air above is \(-10^0C\). The thickness \(L(t)\) of the ice increases with time \(t\). Assuming that all physical properties of air and ice are independent of temperature, \(L(t)\sim L_0t^\alpha\) for large \(t\). The value of \(\alpha\) is
1) \(1/4\)
2) \(1/3\)
3) \(1/2\)
4) \(1\)
Check Answer
Option 3
Q.No:35 CSIR Dec-2023
The solution \( y(x) \) of the differential equation \( y'' + \frac{y}{4} = \frac{x}{2} \), where \( 0 \leq x \leq \pi \),
together with the boundary conditions \( y(0) = y(\pi) = 0 \) is
1) \(
\frac{2}{\pi} \sum_{n=1}^{\infty} (-1)^n \frac{\pi}{n} \frac{\sin nx}{\frac{1}{4}-n^2}
\)
2) \(
\frac{2}{\pi} \sum_{n=1}^{\infty} (-1)^n \frac{\pi}{2n} \frac{\sin nx}{\frac{1}{4}-n^2}
\)
3) \(
\frac{2}{\pi} \sum_{n=1}^{\infty} (-1)^{n+1} \frac{\pi}{n}\frac{\sin nx}{\frac{1}{4}-n^2}
\)
4) \(
\frac{2}{\pi} \sum_{n=1}^{\infty} (-1)^{n+1} \frac{\pi}{2n} \frac{\sin nx}{\frac{1}{4}-n^2}
\)
Check Answer
Option 4
Q.No:36 CSIR June-2024
The general solution for the second-order differential equation
\[
\frac{d^2 y}{dx^2} - y = x \sin x
\]
will be:
1) \( C_1 e^x + C_2 e^{-x} - \frac{1}{2}(x \sin x + \cos x) \)
2) \( C_1 e^x + C_2 e^{-x} + \frac{1}{2} (x \sin x - \cos x) \)
3) \( C_1 e^x + C_2 e^{-x} + \frac{1}{2} x (\sin x - \cos x) \)
4) \( C_1 e^x + C_2 e^{-x} + \frac{1}{2} x (\sin x + \cos x) \)
Check Answer
Option 1
Q.No:37 CSIR June-2025
The solutions of the differential equation
\[
\frac{dy}{dx} = -\frac{x}{y+1}
\]
are a family of
1) ellipses with different eccentricities
2) circles with different centres
3) circles with different radii
4) ellipses with different foci
Check Answer
Option 3
Q.No:38 CSIR June-2025
Let \(P_n(x)\) be a polynomial of degree \(n\) with real coefficients, where
\(n = 0,1,2,3,\ldots\).
If
\[
\int_{2}^{4} P_n(x)\,P_m(x)\,dx = \delta_{mn},
\]
then \(P_1(x)\) is
1) \(\pm \sqrt{\frac{3}{2}}\, (3 - x)\)
2) \(\pm \sqrt{\frac{3}{2}}\, (2 - x)\)
3) \(\pm \sqrt{\frac{3}{2}}\, (1 - x)\)
4) \(\pm \sqrt{3}\, (3 + x)\)
Check Answer
Option 1
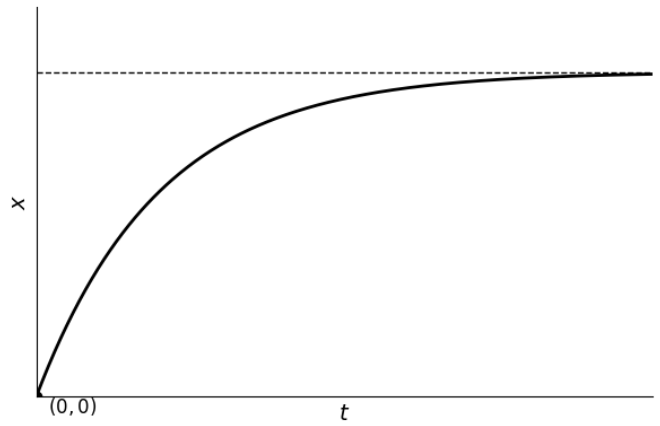
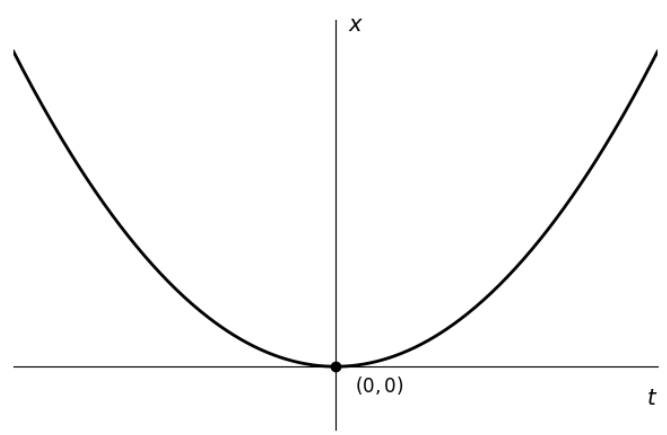
Q.No:39 CSIR June-2025
Which one of the following curves best represents the solution of the
differential equation
\[
\frac{dx}{dt} + x = 1,
\]
with the initial condition \(x(0)=0\)?


Check Answer
Option 1
Q.No:1 GATE-2014
The solution of the differential equation
\[
\frac{d^2 y}{dt^2}-y=0,
\]
subject to the boundary conditions \(y(0)=1\) and \(y(\infty)=0\), is
(A)
\(\cos{t}+\sin{t}\)
(B)
\(\cosh{t}+\sinh{t}\)
(C)
\(\cos{t}-\sin{t}\)
(D)
\(\cosh{t}-\sinh{t}\)
Check Answer
Option D
Q.No:2 GATE-2015
If \(f(x)=e^{-x^2}\) and \(g(x)=|x| e^{-x^2}\), then
(A)
\(f\) and \(g\) are differentiable everywhere
(B)
\(f\) is differentiable everywhere but \(g\) is not
(C)
\(g\) is differentiable everywhere but \(f\) is not
(D)
\(g\) is discontinuous at \(x=0\)
Check Answer
Option B
Q.No:3 GATE-2015
A particle of mass \(0.01 kg\) falls freely in the earth's gravitational field with an initial velocity \(\nu(0)=10 ms^{-1}\). If the air exerts a frictional force of the form, \(f=-k\nu\), then for \(k=0.05 Nm^{-1}s\), the velocity (in \(ms^{-1}\)) at time \(t=0.2 s\) is ______________ (upto two decimal places) (use \(g=10 ms^{-2}\) and \(e=2.72\))
Check Answer
Ans 4.93-4.98
Q.No:4 GATE-2015
A function \(y(z)\) satisfies the ordinary differential equation \(y''+\frac{1}{z}y'-\frac{m^2}{z^2}y=0\), where \(m=0, 1, 2, 3, ...\). Consider the four statements P, Q, R, S as given below.
P: \(z^m\) and \(z^{-m}\) are linearly independent solutions for all values of \(m\)
Q: \(z^m\) and \(z^{-m}\) are linearly independent solutions for all values of \(m>0\)
R: \(\ln{z}\) and \(1\) are linearly independent solutions for \(m=0\)
S: \(z^m\) and \(\ln{z}\) are linearly independent solutions for all values of \(m\)
The correct option for the combinational of valid statements is
(A)
P, R and S only
(B)
P and R only
(C)
Q and R only
(D)
R and S only
Check Answer
Option C
Q.No:5 GATE-2016
Consider the linear differential equation \(\frac{dy}{dx}=xy\). If \(y=2\) at \(x=0\), then the value of \(y\) at \(x=2\) is given by
(A)
\(e^{-2}\)
(B)
\(2e^{-2}\)
(C)
\(e^2\)
(D)
\(2e^2\)
Check Answer
Option D
Q.No:6 GATE-2017
Consider the differential equation \(dy/dx+y\tan{(x)}=\cos{(x)}\). If \(y(0)=0\), \(y(\pi/3)\) is ____________. (up to two decimal places).
Check Answer
Ans 0.51-0.53
Q.No:7 GATE-2018
Given
\[
\frac{d^2 f(x)}{dx^2}-2\frac{df(x)}{dx}+f(x)=0,
\]
and boundary conditions \(f(0)=1\) and \(f(1)=0\), the value of \(f(0.5)\) is ________________ (up to two decimal places).
Check Answer
Ans 0.81-0.84
Q.No:8 GATE-2019
For the differential equation \(\frac{d^2 y}{dx^2}-n(n+1)\frac{y}{x^2}=0\), where \(n\) is a constant, the product of its two independent solutions is
(A)
\(\frac{1}{x}\)
(B)
\(x\)
(C)
\(x^n\)
(D)
\(\frac{1}{x^{n+1}}\)
Check Answer
Option B
Q.No:9 GATE-2020
Which one of the following is a solution of \(\frac{d^2 u(x)}{dx^2}=k^2 u(x)\), for \(k\) real?
(A)
\(e^{-kx}\)
(B)
\(\sin{kx}\)
(C)
\(\cos{kx}\)
(D)
\(\sinh{x}\)
Check Answer
Option A
Q.No:10 GATE-2020
Let
\(
f_n(x)=\left\{
\begin{array}{ll}
0, & x<-\frac{1}{2n} \\
n, & -\frac{1}{2n}<x<\frac{1}{2n} \\
0, & \frac{1}{2n}<x.
\end{array}
\right.
\)
The value of \(\lim_{n\to \infty} \int_{-\infty}^{\infty} f_n(x)\sin{x} dx\) is ___________.
Check Answer
Ans 0
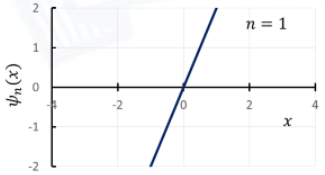
Q.No:11 GATE-2021
If \(y_n(x)\) is solution of the differential equation
\[
y''-2xy'+2ny=0
\]
where \(n\) is an integer and the prime (') denotes differentiation with respect to \(x\), then acceptable plot(s) of \(\psi_n(x)=e^{-x^2/2}y_n(x)\), is(are)



Check Answer
Option B-C
Q.No:12 GATE-2022
Consider the ordinary differential equation
\[
y''-2xy'+4y=0
\]
and its solution \(y(x)=a+bx+cx^2\). Then
(a)
\(a=0, c=-2b\neq 0\)
(b)
\(c=-2a\neq 0, b=0\)
(c)
\(b=-2a\neq 0, c=0\)
(d)
\(c=2a\neq 0, b=0\)
Check Answer
Option b
Q.No:13 GATE-2022
The ordinary differential equation
\[
(1-x^2)y''-xy'+9y=0
\]
has a regular singularity at
(a)
\(-1\)
(b)
\(0\)
(c)
\(+1\)
(d)
no finite value of \(x\)
Check Answer
Option a,c
Q.No:14 GATE-2024
The equation of motion for the forced simple harmonic oscillator is
\[ \ddot{x}(t) + \omega^2 x(t) = F \cos(\omega t) \]
where \(x(t = 0) = 0\) and \(\dot{x}(t = 0) = 0\). Which one of the following options is correct?
(A) \(x(t) \propto t \sin(\omega t)\)
(B) \(x(t) \propto t \cos(\omega t)\)
(C) \(x(t) = \infty\)
(D) \(x(t) \propto e^{\omega t}\)
