Q.No:1 CSIR Dec-2014
If the leading anharmonic correction to the energy of the \(n\)-th vibrational level of a diatomic molecule is \(-x_e\left(n+\frac{1}{2}\right)^2 \hbar \omega\) with \(x_e=0.001\), the total number of energy levels possible is approximately
(1)
\(500\)
(2)
\(1000\)
(3)
\(250\)
(4)
\(750\)
Check Answer
Option 1
Q.No:2 CSIR June-2015
A diatomic molecule has vibrational states with energies \(E_{v}=\hbar \omega\left(v+\frac{1}{2}\right)\) and rotational states with energies \(E_{j} = Bj(j+1)\), where \(v\) and \(j\) are non-negative integers. Consider the transitions in which both the initial and final states are restricted to \(v\leq 1\) and \(j\leq 2\) and subject to the selection rules \(\Delta v=\pm 1\) and \(\Delta j = \pm 1\). Then the largest allowed energy of transition is
(1)
\( \hbar \omega -3B\)
(2)
\(\hbar\omega -B\)
(3)
\(\hbar \omega + 4B\)
(4)
\(2\hbar \omega + B\)
Check Answer
Option 3
Q.No:3 CSIR Dec-2015
The first ionization potential of \(\text{K}\) is \(4.34 \text{ eV}\), the electron affinity of \(\text{Cl}\) is \(3.82 \text{ eV}\) and the equilibrium separation of \(\text{KCl}\) is \(0.3 \text{ nm}\). The energy required to dissociate a \(\text{KCl}\) molecule into a \(\text{K}\) and a \(\text{Cl}\) atom is
(1)
\(8.62 \text{ eV}\)
(2)
\(8.16 \text{ eV}\)
(3)
\(4.28 \text{ eV}\)
(4)
\(4.14 \text{ eV}\)
Check Answer
Option 3
Q.No:4 CSIR Dec-2018
The diatomic molecule HF has an absorption line in the rotational band at \(40 cm^{-1}\) for the isotope \({^{18} F}\). The corresponding line for the isotope \({^{19} F}\) will be shifted by approximately
(1)
\(0.05 cm^{-1}\)
(2)
\(0.33 cm^{-1}\)
(3)
\(0.11 cm^{-1}\)
(4)
\(0.01 cm^{-1}\)
Check Answer
Option 3
Q.No:5 CSIR June-2019
The energy levels corresponding to the rotational motion of a molecule are \(E_J=BJ(J+1) cm^{-1}\) where \(J=0, 1, 2, ...\) and \(B\) is a constant. Pure rotational Raman transitions follow the selection rule \(\Delta J=0, \pm 2\). When the molecule is irradiated, the separation between the closest Stokes and anti-Stokes lines (in cm^{-1}) is
(1)
\(6B\)
(2)
\(12B\)
(3)
\(4B\)
(4)
\(8B\)
Check Answer
Option 2
Q.No:6 CSIR Dec-2019
In a spectrum resulting from Raman scattering, let \(I_R\) denote the intensity of Rayleigh scattering and \(I_S\) and \(I_{AS}\) denote the most intense Stokes line and the most intense anti-Stokes line, respectively. The correct order of these intensities is
(1)
\(I_S> I_R> I_{AS}\)
(2)
\(I_R> I_S> I_{AS}\)
(3)
\(I_{AS}> I_R> I_S\)
(4)
\(I_R> I_{AS}> I_S\)
Check Answer
Option 2
Q.No:7 Assam CSIR Dec-2019
The vibrational frequency of a hydrogen halide molecule is \(\omega=5\times 10^{14} rad.s^{-1}\). Assuming the halogen atom to be heavy compared to the hydrogen atom (\(m_H=1.6\times 10^{-27} kg\)), the force constant of the bond is closest to
(1)
\(80 Nm^{-1}\)
(2)
\(125 Nm^{-1}\)
(3)
\(200 Nm^{-1}\)
(4)
\(400 Nm^{-1}\)
Check Answer
Option 4
Q.No:8 CSIR June-2020
The absorption lines arising from pure rotational effects of \(HCl\) are observed at \(83.03 cm^{-1}, 103.73 cm^{-1}, 145.03 cm^{-1}\) and \(165.51 cm^{-1}\). The moment of inertia of the \(HCl\) molecule is (take \(\frac{\hbar}{2\pi c}=5.6\times 10^{-44} kg-m\))
(a)
\(1.1\times 10^{-48} kg-m^2\)
(b)
\(2.8\times 10^{-47} kg-m^2\)
(c)
\(2.8\times 10^{-48} kg-m^2\)
(d)
\(1.1\times 10^{-42} kg-m^2\)
Check Answer
Option b
Q.No:9 CSIR Sep-2022
The Raman rotational-vibrational spectrum of nitrogen molecules is observed using an incident radiation of wavenumber 12500\(cm^{-1}\). In the first shifted band, the wavenumbers of the observed lines (in \(cm^{-1}\)) are 10150, 10158, 10170, 10182 and 10190. The values of vibrational frequency and rotational constant (\(cm^{-1}\)), respectively,
are
(1)
2330 and 2
(2)
2350 and 2
(3)
2350 and 3
(4)
2330 and 3
Check Answer
Option 1
Q.No:10 CSIR June-2023
Let the separation of the frequencies of the first Stokes and the first anti-Stokes lines in the pure rotational Raman Spectrum of the \(H_2\) molecule be \(\Delta\nu(H_2)\), while the corresponding quantity for \(D_2\) is \(\Delta\nu(D_2)\). The ratio \(\Delta\nu(H_2)/\Delta\nu(D_2)\) is
1) \(0.6\)
2) \(1.2\)
3) \(1\)
4) \(2\)
Check Answer
Option 4
Q.No:11 CSIR Dec-2023
In the rotational-vibrational spectrum of an idealized carbon monoxide (CO) molecule, ignoring rotational-vibrational coupling, two transitions between adjacent vibrational levels with wavelength \(\lambda_1\) and \(\lambda_2\), correspond to the rotational transition from \(J' = 0\) to \(J'' = 1\), and \(J' = 1\) to \(J'' = 0\), respectively. Given that the reduced mass of CO is \(1.2 \times 10^{-26}\) kg, equilibrium bond length of CO is \(0.12\) nm and vibrational frequency is \(5 \times 10^{13}\) Hz, the ratio of \(\frac{\lambda_1}{\lambda_2}\) is closest to
1) 0.9963
2) 0.0963
3) 1.002
4) 1.203
Check Answer
Option 1
Q.No:12 CSIR June-2024
The bond dissociation energy of a molecule is defined as the energy required to dissociate it. For \( H_2 \) and \( H_2^+ \) molecules, the bond dissociation energies are 4.478 eV and 2.651 eV respectively. If the equilibrium bond lengths of both \( H_2 \) and \( H_2^+ \) are identical, the value of the ionization potential of the hydrogen molecule will be closest to
1) 15.427 eV
2) 11.773 eV
3) 20.729 eV
4) 6.471 eV
Check Answer
Option 1
Q.No:13 CSIR June-2025
In a rotational–vibrational spectrum of HCl (\(^{35}\mathrm{Cl}\)),
the first \(R\)-branch line and the first \(P\)-branch line are observed at
\[
\lambda^{-1} = 2906\ \text{cm}^{-1}, \qquad
\lambda^{-1} = 2865\ \text{cm}^{-1}.
\]
The equilibrium bond length of this molecule would be closest to
1) \(0.2\ \text{Å}\)
2) \(1.3\ \text{Å}\)
3) \(13\ \text{Å}\)
4) \(2.1\ \text{Å}\)
Check Answer
Option 2
Q.No:1 GATE-2012
The first Stokes line of a rotational Raman spectrum is observed at \(12.96 cm^{-1}\). Considering the rigid rotor approximation, the rotational constant is given by
(A)
\(6.48 cm^{-1}\)
(B)
\(3.24 cm^{-1}\)
(C)
\(2.16 cm^{-1}\)
(D)
\(1.62 cm^{-1}\)
Check Answer
Option C
Q.No:2 GATE-2012
Match the typical spectroscopic regions specified in \({\bf Group I}\) with the corresponding type of transitions in \({\bf Group II}\).

(A)
(P, i); (Q, iii); (R, ii); (S, iv)
(B)
(P, ii); (Q, iv); (R, i); (S, iii)
(C)
(P, iii); (Q, i); (R, iv); (S, ii)
(D)
(P, iv); (Q, i); (R, ii); (S, iii)
Check Answer
Option C
Q.No:3 GATE-2012
The equilibrium vibration frequency for an oscillator is observed at \(2990 cm^{-1}\). The ratio of the frequencies corresponding to the first and the fundamental spectral lines is \(1.96\). Considering the oscillator to be anharmonic, the anharmonicity constant is
(A)
\(0.005\)
(B)
\(0.02\)
(C)
\(0.05\)
(D)
\(0.1\)
Check Answer
Option B
Q.No:4 GATE-2013
The spacing between vibrational energy levels in \({CO}\) molecule is found to be \(8.44\times 10^{-2} eV\). Given that the reduced mass of \({CO}\) is \(1.14\times 10^{-26} kg\), Planck's constant is \(6.626\times 10^{-34} Js\) and \(1 eV=1.6\times 10^{-19} J\). The force constant of the bond in \({CO}\) molecule is
(A)
\(1.87 N/m\)
(B)
\(18.7 N/m\)
(C)
\(187 N/m\)
(D)
\(1870 N/m\)
Check Answer
Option C
Q.No:5 GATE-2014
The moment of inertia of a rigid diatomic molecule \(A\) is \(6\) times that of another rigid diatomic molecule \(B\). If the rotational energies of the two molecules are equal, then the corresponding values of the rotational quantum numbers \(J_A\) and \(J_B\) are
(A)
\(J_A=2, J_B=1\)
(B)
\(J_A=3, J_B=1\)
(C)
\(J_A=5, J_B=0\)
(D)
\(J_A=6, J_B=1\)
Check Answer
Option B
Q.No:6 GATE-2015
The excitation wavelength of laser in a Raman effect experiment is \(546 nm\). If the Stokes' line is observed at \(552 nm\), then the wavenumber of the anti-Stokes' line (in \(cm^{-1}\)) is ___________
Check Answer
Ans 18513-18519
Q.No:7 GATE-2015
Match the phrases in Group I and Group II ad identify the correct option.

(A)
(P-i), (Q-ii), (R-iii), (S-iv)
(B)
(P-ii), (Q-i), (R-iv), (S-iii)
(C)
(P-iii), (Q-iv), (R-i), (S-ii)
(D)
(P-iii), (Q-i), (R-iv), (S-ii)
Check Answer
Option D
Q.No:8 GATE-2015
In a rigid-rotator of mass \(M\), if the energy of the first excited state is \(1 meV\), then the fourth excited state energy (in meV) is _________________
Check Answer
Ans 10
Q.No:9 GATE-2016
The molecule \({^{17} O_2}\) is
(A)
Raman active but not NMR (nuclear magnetic resonance) active.
(B)
Infrared active and Raman active but not NMR active.
(C)
Raman active and NMR active.
(D)
Only NMR active.
Check Answer
Option C
Q.No:10 GATE-2017
Which one of the following gases of diatomic molecules is Raman, infrared, and NMR active?
(A)
\({^{1} H}-{^{1} H}\)
(B)
\({^{12} C}-{^{16} O}\)
(C)
\({^{1} H}-{^{35} Cl}\)
(D)
\({^{16} O}-{^{16} O}\)
Check Answer
Option C
Q.No:11 GATE-2018
The expression for the second overtone frequency in the vibrational absorption spectra of a diatomic molecule in terms of the harmonic frequency \(\omega_e\) and anharmonicity constant \(x_e\) is
(A)
\(2\omega_e(1-x_e)\)
(B)
\(2\omega_e(1-3x_e)\)
(C)
\(3\omega_e(1-2x_e)\)
(D)
\(3\omega_e(1-4x_e)\)
Check Answer
Option D
Q.No:12 GATE-2021
The spacing between two consecutive S-branch lines of the rotational Raman spectra of hydrogen gas is \(243.2 cm^{-1}\). After excitation with a laser of wavelength \(514.5 nm\), the Stoke's line appeared at \(17611.4 cm^{-1}\) for a particular energy level. The wavenumber (rounded off to the nearest integer), in \(cm^{-1}\), at which Stoke's line will appear for the next higher energy level is _____________.
Check Answer
Ans 17367-17371
Q.No:13 GATE-2022
In a solid, a Raman line observed at \(300\hspace{1mm}\text{cm}^{-1}\) has intensity of Stokes line four times that of the anti-Stokes line. The temperature of the sample is --------------- \(\text{K}\). (Round off to the nearest integer) (\(1\hspace{1mm}\text{cm}^{-1}\equiv 1.44\hspace{1mm}\text{K}\))
Check Answer
Ans 311-312
Q.No:14 GATE-2022
In a diatomic molecule of mass \(M\), electronic, rotational and vibrational energy scales are of magnitude \(E_e, E_R\) and \(E_V\), respectively. The spring constant for the vibrational energy is determined by \(E_e\). If the electron mass is \(m\) then
(a)
\(E_R\sim \frac{m}{M}E_e\)
(b)
\(E_R\sim \sqrt{\frac{m}{M}}E_e\)
(c)
\(E_V\sim \sqrt{\frac{m}{M}}E_e\)
(d)
\(E_V\sim \left(\frac{m}{M}\right)^{1/4} E_e\)
Check Answer
Option a,c
Q.No:15 GATE-2023
It is given that the electronic ground state of a diatomic molecule \(X_2\) has even parity and the nuclear spin of \(X\) is 0. Which one of the following is the CORRECT statement with regard to the rotational Raman spectrum (\(J\) is the rotational quantum number) of this molecule?
(A)
Lines of all \(J\) values are present
(B)
Lines have alternating intensity in the ratio of 3: 1
(C)
Lines of only even \(J\) values are present
(D)
Lines of only odd \(J\) values are present
Check Answer
Option C
Q.No:16 GATE-2024
Atomic numbers of V, Cr, Fe and Zn are 23, 24, 26 and 30, respectively. Which one of the following materials does NOT show an electron spin resonance (ESR) spectra?
(A) V
(B) Cr
(C) Fe
(D) Zn
Check Answer
Option D
Q.No:17 GATE-2024
The mean distance between the two atoms of HD molecule is \( r \), where H and D denote hydrogen and deuterium, respectively. The mass of the hydrogen atom is \( m_H \). The energy difference between two lowest lying rotational states of HD in multiples of \( \hbar^2 / (m_H r^2) \) is
(A) \(\frac{3}{2}\)
(B) \(\frac{2}{3}\)
(C) \(6\)
(D) \(\frac{4}{3}\)
Check Answer
Option A
Q.No:18 GATE-2025
The potential energy of two diatomic molecules \(P\) and \(Q\), having the
same reduced mass, is shown in the figure.
According to this diagram, which of the following option(s) is/are correct?
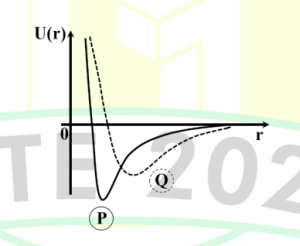
A) The equilibrium inter-nuclear distance of \(Q\) is more than that of \(P\).
B) The total energy \(E = 0\) separates bound and unbound states of the molecules.
C) The lowest vibrational frequency of \(P\) is larger than that of \(Q\).
D) The dissociation energy of \(Q\) is more than that of \(P\).
Check Answer
Option A,B,C
Q.No:1 JEST-2016
The \({H_{2}}\) molecule has a reduced mass \(M=8.35\times 10^{-28} kg\) and an equilibrium internuclear distance \(R=0.742\times 10^{-10} m\). The rotational energy in terms of the rotational quantum number \(J\) is:
(A)
\(E_{\text{rot}}(J)=7J(J-1) meV\)
(B)
\(E_{\text{rot}}(J)=\frac{5}{2}J(J+1) meV\)
(C)
\(E_{\text{rot}}(J)=7J(J+1) meV\)
(D)
\(E_{\text{rot}}(J)=\frac{5}{2}J(J-1) meV\)
Check Answer
Option Grace
Q.No:1 TIFR-2012
The intensity of light coming from a distant star is measured using two identical instruments A and B, where A is placed in a satellite outside the Earth's atmosphere, and B is placed on the Earth's surface. The results are as follows:

Assuming that there is scattering, but no absorption of light in the Earth's atmosphere at these wavelengths, the value of \(x\) can be estimated as
(a)
\(137\)
(b)
\(147\)
(c)
\(157\)
(d)
\(167\)
(e)
\(177\)
Check Answer
Option d
Q.No:2 TIFR-2016
Two homonuclear diatomic molecules produce different rotational spectra, even though the atoms are known to have identical chemical properties. This leads to the conclusion that the atoms must be
(a)
isotopes, i.e. with the same atomic number.
(b)
isobars, i.e. with the same atomic weight.
(c)
isotones, i.e. with the same neutron number.
(d)
isomers, i.e. with the same atomic number and weight.
Check Answer
Option a
Q.No:3 TIFR-2017
The separation between neighbouring absorption lines in a pure rotational spectrum of the hydrogen bromide \(({HBr})\) molecule is \(2.23 \hspace{1mm}\text{meV}\). If this molecule is considered as a rigid rotor and the atomic mass number of \({Br}\) is \(80\), the corresponding absorption line separation in deuterium bromide (\({DBr}\)) molecule, in units of \(\text{meV}\), would be
(a)
\(2.234\)
(b)
\(1.115\)
(c)
\(1.128\)
(d)
\(4.461\)
Check Answer
Option c
Q.No:4 TIFR-2022
Treat the hydrogen molecule \(H_2\) as a rigid rotator. The next-to largest wavelength in its rotational spectrum is about 111 \(\mu\)m. From this it can be estimated that the separation between the pair of hydrogen atoms is about
(a)
0.12 nm
(b)
24.4 nm
(c)
61.4 nm
(d)
3.17 \(\mu\)m
Check Answer
Option a
Q.No:5 TIFR-2023
The minimum energy required to dissociate a hydrogen molecule \(H_2\)into two atoms is 4.5 eV. If the electron affinity of hydrogen atom is 0.75 eV, the minimum energy required to dissociate the hydrogen molecule into \(H^+\) and \(H^-\) would be
(a)
14.35 eV
(b)
5.25 eV
(c)
17.35 eV
(d)
18.85 eV
Check Answer
Option c
Q.No:6 TIFR-2023
Consider a diatomic molecule with two atoms of masses \(m_1=1\) a.m.u. and \(m_2=8\) a.m.u. which are separated by a distance \(r\) and bound by an effective interaction potential of the form
\[V(r)=\epsilon (\frac{a^4}{4r^2}-\frac{b^2}{2r^2})\]
where \(\epsilon= 4 \times 10^{-18} J , a=b=1 \hspace{1mm} \text{Angstrom}, \) and \(1 \hspace{2mm} \text{a.m.u }\approx 1.6 \times 10^{-27} kg.\)
Making a small oscillations approximation, the transition frequency corresponding to the vibrational spectra of the molecule is approximately
(a)
\(1.2 \times 10^{14} \) Hz
(b)
\(0.4 \times 10^{14} \) Hz
(c)
\(7.5 \times 10^{14} \) Hz
(d)
\(3.6 \times 10^{14} \) Hz
Check Answer
Option a
Q.No:7 TIFR-2025
\(O_2\) is a linear molecule.
The bond length of the oxygen molecule is \(1.2\,\text{Å}\), and the mass of
an oxygen atom is \(2.7 \times 10^{-26}\,\text{kg}\).
A neutron strikes an \(O_2\) molecule and loses energy by exciting a
rotational energy level of \(O_2\).
Which of the following is the best estimate of the lowest amount of energy
the neutron would have to transfer to the \(O_2\) molecule?
(Take the transfer of translational kinetic energy to be negligible.)
a)\(3.6 \times 10^{-4}\,\text{eV}\)
b) \(7.2 \times 10^{-4}\,\text{eV}\)
c) \(1.8 \times 10^{-4}\,\text{eV}\)
d) \(1.4 \times 10^{-3}\,\text{eV}\)

Qs4. Csir Dec 2018
Option 3 ( not option 2)