Q.No:1 CSIR Jun-2015
Consider the differential equation
\(\frac{dy}{dx}=x^{2} - y\) with the initial condition \(y = 2\) at \(x = 0\). Let \(y_{(1)}\) and \(y_{(1/2)}\) be the solutions at \(x = 1\) obtained using Euler's forward algorithm with step size 1 and \(\frac{1}{2}\) respectively.
The value of \(\bigg(y_{(1)} - Y_{(1/2)}\bigg)/y_{(1/2)}\) is
(1)
\(-1/2\)
(2)
\(-1\)
(3)
\(1/2\)
(4)
\(1\)
Check Answer
Option 2
Q.No:2 CSIR Dec-2015
The value of the integral \(\int_{0}^{8} \frac{1}{x^2+5} dx\), evaluated using Simpson's \(\frac{1}{3}\) rule with \(h=2\), is
(1)
\(0.565\)
(2)
\(0.620\)
(3)
\(0.698\)
(4)
\(0.736\)
Check Answer
Option 1
Q.No:3 CSIR Jun-2016
In finding the roots of the polynomial \(f(x)=3x^3-4x-5\) using the iterative Newton-Raphson method, the initial guess is taken to be \(x=2\). In the next iteration its value is nearest to
(1)
\(1.671\)
(2)
\(1.656\)
(3)
\(1.559\)
(4)
\(1.551\)
Check Answer
Option 2
Q.No:4 CSIR Dec-2016
A stable asymptotic solution of the equation \(x_{n+1}=1+\frac{3}{1+x_n}\) is \(x=2\). If we take \(x_n=2+\epsilon_n\) and \(x_{n+1}=2+\epsilon_{n+1}\), where \(\epsilon_n\) and \(\epsilon_{n+1}\) are both small, the ratio \(\epsilon_{n+1}/\epsilon_n\) is approximately
(1)
\(-\frac{1}{2}\)
(2)
\(-\frac{1}{4}\)
(3)
\(-\frac{1}{3}\)
(4)
\(-\frac{2}{3}\)
Check Answer
Option 3
Q.No:5 CSIR Dec-2016
Given the values \(\sin{45^{\circ}}=0.7071, \sin{50^{\circ}}=0.7660, \sin{55^{\circ}}=0.8192\) and \(\sin{60^{\circ}}=0.8660\), the approximate value of \(\sin{52^{\circ}}\), computed by Newton's forward difference method, is
(1)
\(0.804\)
(2)
\(0.776\)
(3)
\(0.788\)
(4)
\(0.798\)
Check Answer
Option 3
Q.No:6 CSIR Jun-2017
The interval \([0, 1]\) is divided into \(2n\) parts of equal length to calculate the integral \(\int_0^1 e^{i2\pi x} dx\) using Simpson's \(\frac{1}{3}\)-rule. What is the minimum value of \(n\) for the result to be exact?
(1)
\(\infty\)
(2)
\(2\)
(3)
\(3\)
(4)
\(4\)
Check Answer
Option 2
Q.No:7 CSIR Dec-2017
The differential equation \(\frac{dy(x)}{dx}=\alpha x^2\), with the initial condition \(y(0)=0\), is solved using Euler's method. If \(y_E(x)\) is the exact solution and \(y_N(x)\) the numerical solution obtained using \(n\) steps of equal length, then the relative error \(\left|\frac{(y_N(x)-y_E(x))}{y_E(x)}\right|\) is proportional to
(1)
\(1/n^2\)
(2)
\(1/n^3\)
(3)
\(1/n^4\)
(4)
\(1/n\)
Check Answer
Option 4
Q.No:8 CSIR Dec-2017
The interval \([0, 1]\) is divided into \(n\) parts of equal length to calculate the integral \(\int_{0}^{1} e^{i2\pi x} dx\) using the trapezoidal rule. The minimum value of \(n\) for which the result is exact, is
(1)
\(2\)
(2)
\(3\)
(3)
\(4\)
(4)
\(\infty\)
Check Answer
Option 1
Q.No:9 CSIR Jun-2018
The fractional error in estimating the integral \(\int_{0}^{1} x dx\) using Simpson's \(\frac{1}{3}\)-rule, using a step size \(0.1\), is nearest to
(1)
\(10^{-4}\)
(2)
\(0\)
(3)
\(10^{-2}\)
(4)
\(3\times 10^{-4}\)
Check Answer
Option 2
Q.No:10 CSIR Dec-2018
The value of the integral \(\int_{0}^{1} x^2 dx\), evaluated using the trapezoidal rule with a step size of \(0.2\), is
(1)
\(0.30\)
(2)
\(0.39\)
(3)
\(0.34\)
(4)
\(0.27\)
Check Answer
Option 3
Q.No:11 CSIR Jun-2019
If the Newton-Raphson method is used to find the positive root of the equation \(x=2\sin{x}\), the iteration equation is
(1)
\(x_{n+1}=\frac{2x_n-2(\sin{x_n}+x_n \cos{x_n})}{1-2\cos{x_n}}\)
(2)
\(x_{n+1}=\frac{2(\sin{x_n}-x_n \cos{x_n})}{1-2\cos{x_n}}\)
(3)
\(x_{n+1}=\frac{x_n^2-1+2(\cos{x_n}-x_n \sin{x_n})}{x_n-2\sin{x_n}}\)
(4)
\(x_{n+1}=\frac{x_n^2-1-2(\cos{x_n}+\sin{x_n})}{x_n-2\sin{x_n}}\)
Check Answer
Option 2
Q.No:12 CSIR Dec-2019
The positive zero of the polynomial \(f(x)=x^2-4\) is determined using Newton-Raphson method, using an initial guess \(x=1\). Let the estimate, after two iterations, be \(x^{(2)}\). The percentage error \(\left|\frac{x^{(2)}-2}{2}\right|\times 100\%\) is
(1)
\(7.5\%\)
(2)
\(5.0\%\)
(3)
\(1.0\%\)
(4)
\(2.5\%\)
Check Answer
Option 4
Q.No:13 CSIR Assam Dec-2019
The second order Runge-Kutta method to find an approximate solution \(y(x)\) of the boundary value problem \(\frac{dy}{dx}=f(x, y)\) with the boundary condition \(y(0)=y_0\) uses
\[
y_{n+1}=y_n+hf\left(x_n+\frac{h}{2}, y_n+\frac{h}{2}f(x_n, y_n)\right)
\]
where \(x_n=nh\) and \(y_n\) is the approximation to \(y\) after \(n\) iterations. If \(f(x, y)=2y, y_0=2\) and step size \(h=0.02\), then \(y_2\) and absolute error \(|y(x_2)-y_2|\) after two iterations are, respectively,
(1)
\(2(1.0408)^2\) and \(2|e^{0.04}-(1.0408)^2|\)
(2)
\(2(1.0204)^2\) and \(2|e^{0.08}-(1.0204)^2|\)
(3)
\(2(1.0404)^2\) and \(2|e^{0.08}-(1.0404)^2|\)
(4)
\(2(1.0408)^2\) and \(2|e^{0.08}-(1.0408)^2|\)
Check Answer
Option 4
Q.No:14 CSIR Jun-2019
Using the following values of \(x\) and \(f(x)\)
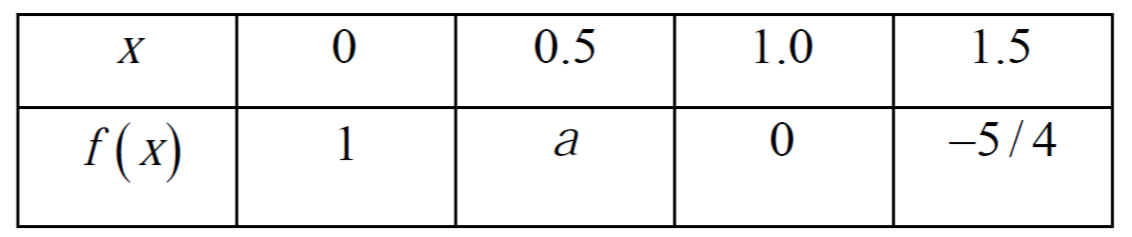
the integral \(I=\int_{0}^{1.5} f(x) dx\), evaluated by the Trapezoidal rule, is \(5/16\). The value of \(a\) is
(1)
\(3/4\)
(2)
\(3/2\)
(3)
\(7/4\)
(4)
\(19/24\)
Check Answer
Option 1
Q.No:15 CSIR Feb-2022
The Newton-Raphson method is to be used to determine the reciprocal of the number
\(x=4\) . If we start with the initial guess \(0.20\) then after the first iteration the reciprocal is
(1)
\(0.23\)
(2)
\(0.24\)
(3)
\(0.25\)
(4)
\(0.26\)
Check Answer
Option 2
Q.No:16 CSIR June-2023
The bisection method is used to find a zero \(x_0\) of the polynomial \(f(x)=x^3-x^2-1\). Since \(f(1)=-1\), while \(f(2)=3\), the values \(a=1\) and \(b=2\) are chosen as the boundaries of the interval in which the \(x_0\) lies. If the bisection method is iterated three times, the resulting value of \(x_0\) is
1) \(\frac{15}{8}\)
2) \(\frac{13}{8}\)
3) \(\frac{11}{8}\)
4) \(\frac{9}{8}\)
Check Answer
Option 3
Q.No:17 CSIR dec-2023
Given the data points
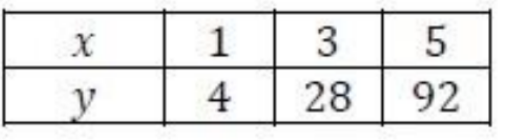
using Lagrange's method of interpolation, the value of \( y \) at \( x = 4 \) is closest to
1) 54
2) 55
3) 53
4) 56
Check Answer
Option 2
Q.No:18 CSIR June-2024
The integral \(I = \int_{0}^{1} \frac{2x}{1+x^2} dx\) is estimated using Simpson's \(1/3\)rd rule with a grid value of \(h = 0.5\). The difference \((I_{estimated} - I_{exact})\) is closest to
1) \(0.007\)
2) \(0.001\)
3) \(0.0007\)
4) \(-0.005\)
Check Answer
Option 1
Q.No:1 JEST-2014
The value of \(\int_{0.2}^{2.2} xe^x dx\) by using the one-segment trapezoidal rule is close to
(a)
\(11.672\)
(b)
\(11.807\)
(c)
\(20.099\)
(d)
\(24.119\)
Check Answer
Option c
Q.No:1 TIFR-2017
Evaluate the expression
\[
n!\int_0^A dx_{n-1} \int_0^{x_{n-1}} dx_{n-2} \int_0^{x_{n-2}} dx_{n-3}\cdots \int_0^{x_3} dx_2 \int_0^{x_2} dx_1 \int_0^{x_1} dx_0
\]
