Q.No:1 TIFR-2012
Two masses \(M_1\) and \(M_2\) (\(M_1<M_2\)) are suspended from a perfectly rigid horizontal support by a system of three taut massless wires \(W_1, W_2\) and \(W_3\), as shown in the figure. All the three wires have identical cross-sections and elastic properties and are known to be very strong.
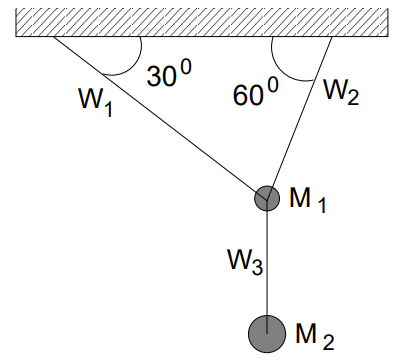
If the mass \(M_2\) is increased gradually, but without limit, we should expect the wires to break in the following order:
(a)
first \(W_2\), then \(W_1\)
(b)
first \(W_1\), then \(W_2\)
(c)
first \(W_2\), then \(W_3\)
(d)
first \(W_3\)
Check Answer
Option d
Q.No:2 TIFR-2012
A high-velocity missile, travelling in a horizontal line with a kinetic energy of \(3.0\) Giga-Joules (GJ), explodes in flight and breaks into two pieces A and B of equal mass. One of these pieces (A) flies off in a straight line perpendicular to the original direction in which the missile was moving and its kinetic energy is found to be \(2.0 GJ\). If gravity can be neglected for such high-velocity projectiles, it follows that the other piece (B) flew off in a direction at an angle with the original direction of
(a)
\(30^{\circ}\)
(b)
\(33^{\circ}24'\)
(c)
\(45^{\circ}\)
(d)
\(60^{\circ}\)
Check Answer
Option a
Q.No:3 TIFR-2012
An ideal liquid of density \(1 gm/cc\) is flowing at a rate of \(10 gm/s\) through a tube with varying cross-section, as shown in the figure.

Two pressure gauges attached at the points \(A\) and \(B\) (see figure) show readings of \(P_A\) and \(P_B\) respectively. If the radius of the tube at the points \(A\) and \(B\) is \(0.2 cm\) and \(1.0 cm\) respectively, then the difference in pressure (\(P_B-P_A\)), in units of dyne \(cm^{−2}\), is closest to
(a)
\(100\)
(b)
\(120\)
(c)
\(140\)
(d)
\(160\)
Check Answer
Option b
Q.No:4 TIFR-2013
A two-dimensional vector \(\vec{A}(t)\) is given by
\[
\vec{A}(t)=\hat{i}\sin{2t}+\hat{j}\cos{3t}.
\]
Which of the following graphs best describes the locus of the tip of the vector, as \(t\) is varied from \(0\) to \(2\pi\)?

Check Answer
Option c
Q.No:5 TIFR-2013
A stone is dropped vertically from the top of a tower of height \(40 m\). At the same time a gun is aimed directly at the stone from the ground at a horizontal distance \(30 m\) from the base of the tower and fired. If the bullet from the gun is to hit the stone before it reaches the ground, the minimum velocity of the bullet must be, approximately,
(b)
\(57.4 ms^{-1}\)
(b)
\(27.7 ms^{-1}\)
(b)
\(17.7 ms^{-1}\)
(b)
\(7.4 ms^{-1}\)
Check Answer
Option c
Q.No:6 TIFR-2013
Consider the uniform solid right cone depicted in the figure on the right. This cone has mass \(M\) and a circular base of radius \(r\). If the moment of inertia of the cone about an axis parallel to the \(X\) axis passing through the centre of mass \(O_{\text{C.M.}}\) (see figure) is given by
\[
\frac{3}{80}M(4r^2+h^2)
\]
then the moment of inertia about another axis parallel to the \(X\) axis, but passing through the point \(O_{\text{r}}\) (see figure), is

(a)
\(\frac{3}{80}M(4r^2+h^2)\)
(b)
\(\frac{1}{20}M(23r^2+2h^2)\)
(c)
\(\frac{3}{40}M(2r^2+h^2)\)
(d)
\(\frac{1}{30}M(15r^2+4h^2)\)
Check Answer
Option c
Q.No:7 TIFR-2013
In the laboratory frame two electrons are shot at each other with equal and opposite velocities \(\vec{u}_1\) and \(\vec{u}_2\) respectively, but not along the same straight line, as shown below.

Each electron will be acted on by the Coulomb repulsion due to the other, as well as the Lorentz force due to its own motion in the magnetic field created by the other. Which of the diagrams given below best describes the final velocities \(\vec{v}_1\) and \(\vec{v}_2\) of these electrons?
[ You may assume that the electrons are distinguishable.]

Check Answer
Option b
Q.No:8 TIFR-2013
A particle with time-varying mass
\[
m(t)=m_0(1-t/\tau),
\]
where \(m_0\) and \(\tau\) are positive constants, moves along the \(x\)-axis under the action of a constant positive force \(F\) for \(0\leq t<\tau\). If the particle is at rest at time \(t=0\), then at time \(t=t\), its velocity \(v\) will be
(a)
\(-\frac{\tau F}{m_0}\log{\left(1-\frac{t}{\tau}\right)}\)
(b)
\(-\frac{Ft}{m_0}\log{\frac{t}{\tau}}\)
(c)
\(-\frac{Ft}{m_0}\log{\left(1-\frac{t}{\tau}\right)^{-1}}\)
(d)
\(\frac{\tau F}{m_0}\left(1-\frac{t}{\tau}\right)\)
Check Answer
Option c
Q.No:9 TIFR-2013
The negative image on the right represents a very small portion of the night sky at a very high resolution. Notice the broken ring(s) around the central bright object in the middle of the picture. These are most likely to be due to

(a)
debris from a smaller object torn apart by tidal forces
(b)
gas clouds forming the remnant of a supernova explosion
(c)
ice collected on the lens used for taking the picture
(d)
gravitational lensing of a distant object by the central massive object
Check Answer
Option d
Q.No:10 TIFR-2014
The directed beam from a small but powerful searchlight placed on the ground tracks a small plane flying horizontally at a fixed height \(h\) above the ground with a uniform velocity \(\nu\), as shown in the figure below.
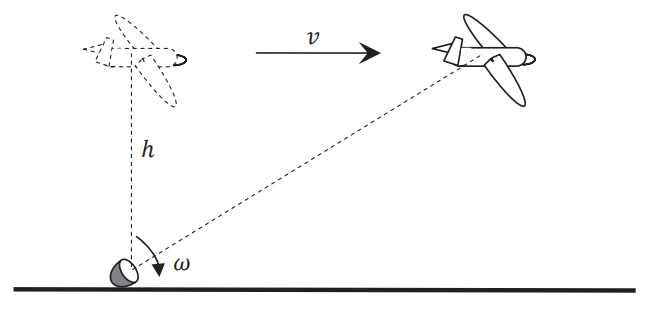
If the searchlight starts rotating with an instantaneous angular velocity \(\omega_0\) at time \(t=0\) when the plane was directly overhead, then at a later time \(t\), its instantaneous angular velocity \(\omega(t)\) is given by
(a)
\(\omega_0 \exp{(-\omega_0 t)}\)
(b)
\(\frac{\omega_0}{1+\tan{\omega_0 t}}\)
(c)
\(\frac{\omega_0}{1+\omega_0^2 t^2}\)
(d)
\(\frac{\omega_0}{1-\omega_0 t+\frac{1}{2}\omega_0^2 t^2}\)
Check Answer
Option c
Q.No:11 TIFR-2014
A uniform ladder of length \(2L\) and mass \(m\) leans against a wall in a vertical plane at an angle \(\theta\) to the horizontal. The floor is rough, having a coefficient of static friction \(\mu\). A person of mass \(m\) stands on the ladder at a distance \(D\) from its base (see figure). If the wall is frictionless, the maximum distance (\(D_{\text{max}}\)) up the ladder that the person can reach before the ladder slips is
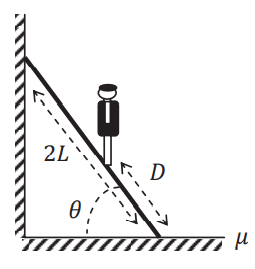
(a)
\(2\mu L\left(1+\frac{m}{M}\right)\tan{\theta}\)
(b)
\(\left\{2\mu\left(1+\frac{m}{M}\right)\tan{\theta}-\frac{m}{M}\right\}L\)
(c)
\(\mu L\tan{\theta}\)
(d)
\(2\mu L\frac{m}{M}\tan{\theta}\)
Check Answer
Option b
Q.No:12 TIFR-2014
The Conservation Principles for energy, linear momentum and angular momentum arise from the necessity that
(a)
the laws of physics should not involve infinite quantities.
(b)
internal forces on a body should cancel out, by Newton's (third) law of action and reaction.
(c)
physical measurements should be independent of the origin and orientation of the coordinate system.
(d)
the laws of physics should be independent of the state of rest or motion of the observer.
Check Answer
Option c
Q.No:13 TIFR-2014
A weight \(W\) is suspended from a rigid support by a hard spring with stiffness constant \(K\). The spring is enclosed in a hard plastic sleeve, which prevents horizontal motion, but allows vertical oscillations (see figure). A simple pendulum of length \(\ell\) with a bob of mass \(m\) (\(mg\ll W\)) is suspended from the weight \(W\) and is set oscillating in a horizontal line with a small amplitude. After some time has passed, the weight \(W\) is observed to be oscillating up and down with a large amplitude (but not hitting the sleeve).

It follows that the stiffness constant
(a)
\(K=\frac{4W}{\ell}\)
(b)
\(K=\frac{2W}{\ell}\)
(c)
\(K=\frac{W}{\ell}\)
(d)
\(K=\frac{W}{2\ell}\)
Check Answer
Option a
Q.No:14 TIFR-2014
Assume that the Earth is a uniform sphere of radius \(R\), rotating about its axis with a uniform angular velocity \(\omega\). A rocket is launched from the Equator in a direction due North. If it keeps on flying at a uniform speed \(\nu\) (neglecting air resistance), the highest latitude that can be achieved is
(a)
\(\frac{\pi}{2}\)
(b)
\(\frac{\pi}{2}-(\pi-2)\frac{\omega R}{\nu}\)
(c)
\(\frac{\pi}{2}-(\pi+2)\frac{\omega R}{\nu}\)
(d)
\(\frac{\pi}{2}\left(1-\frac{2\omega R}{\nu}\right)\)
Check Answer
Option b
Q.No:15 TIFR-2014
A group of alien astronomers far away from the solar system tries to find out if the Sun (visible to them as a small yellow star) has planets orbiting around it. The method they use is to look for wobbles in the motion of the Sun induced by the planet(s) revolving around it (if any). To detect this motion, they build a high-resolution spectrometer which can measure the Doppler shift in frequency of a \(600 nm\) line in the solar spectrum with an accuracy of \(1\) in \(10^6\).
Given that the Sun has a mass \(2\times 10^{30} kg\) and that Earth (mass \(6\times 10^{24} kg\), orbital velocity \(3\times 10^4 ms^{-1}\)) and Jupiter (mass \(2\times 10^{27} kg\), orbital velocity \(1.5\times 10^4 ms^{-1}\)) are two typical planets, one could predict that the experiments conducted by the aliens would find
(a)
evidence for both the planets Earth and Jupiter.
(b)
evidence for the planet Jupiter, but not for the planet Earth.
(c)
no evidence for any planets orbiting the Sun.
(d)
evidence for planets, but will not be able to tell how many.
Check Answer
Option c
Q.No:16 TIFR-2015
A car starts from rest and accelerates under a force \(F\) increasing linearly in time as \(F=at\) where \(a\) is a constant. At time \(t_1>0\), the force \(F\) is suddenly switched off. At a later time \(t_2>t_1\), brakes are applied resulting in a force \(F'\) whose magnitude increases linearly with time, \(F'=-a(t-t_2)\) where \(a\) is the same constant as before. Which of the following graphs would best represent the change in the position of the car \(x(t)\) with time?
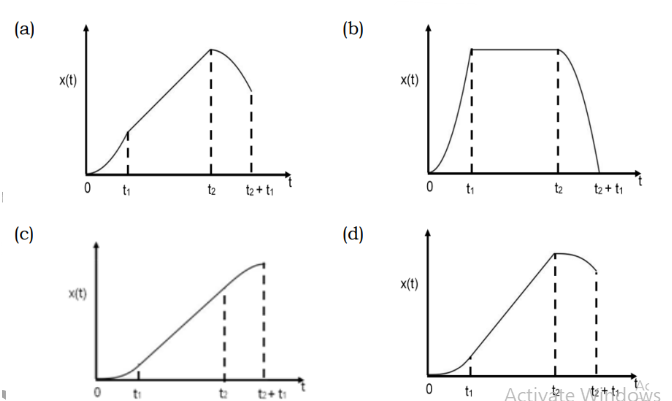
Check Answer
Option c
Q.No:17 TIFR-2015
In the Earth's atmosphere, a localised low-pressure region (shaded in diagrams) develops somewhere in the southern hemisphere. Which one of the following diagrams represents the correct air flow pattern as observed from a satellite?
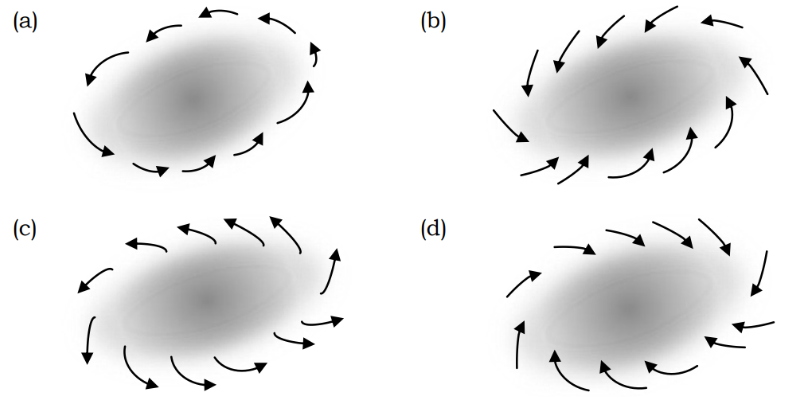
Check Answer
Option d
Q.No:18 TIFR-2015
Two cylinders A and B of the same length \(L\) and outer radius \(R\) were placed at the same height \(h\) on an inclined plane at an angle \(\varphi\) with the horizontal (see figure). Starting from rest, each cylinder was allowed to roll down the plane without slipping. It was found that A reached the end of the inclined plane earlier than B. Which of the following possibilities could be true?

(a)
A is hollow and made of copper; B is hollow and made of copper; B is heavier than A.
(b)
A is solid and made of copper; B is solid and made of aluminium.
(c)
A is hollow and made of aluminium; B is solid and made of aluminium.
(d)
A is solid and made of copper; B is hollow and made of copper.
Check Answer
Option d
Q.No:19 TIFR-2015
A thin uniform rod of length \(2l\) and mass \(M\) is pivoted at one end \(P\) on a horizontal plane (see figure). A ball of mass \(m\ll M\) and speed \(\nu_0\) strikes the free end of the rod perpendicularly and bounces back with velocity \(\nu_f\) along the original line of motion as shown in the fig. If the collision is perfectly elastic the magnitude of \(\nu_f\) is
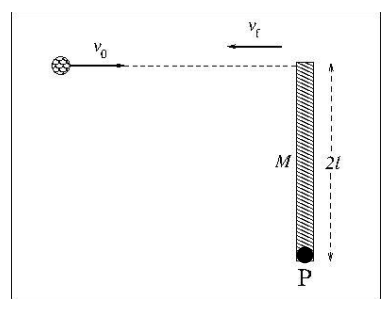
(a)
\(\frac{M-4m}{M+4m}\nu_0\)
(b)
\(\frac{M+4m}{M-4m}\nu_0\)
(c)
\(\frac{M-3m}{M+3m}\nu_0\)
(d)
\(\frac{M+3m}{M-3m}\nu_0\)
Check Answer
Option c
Q.No:20 TIFR-2015
Solar radiation tends to push any particle inside solar system away from the Sun. Consider a spherical dust particle of specific gravity \(6.0\) and no angular momentum about the Sun. What should be its minimum radius so that it does not escape from the solar system? Take the solar luminosity to be \(3.8\times 10^{26} W\).
(a)
\(10^{-6} \mu m\)
(b)
\(0.01 \mu m\)
(c)
\(0.1 \mu m\)
(d)
\(10 \mu m\)
Check Answer
Option c
Q.No:21 TIFR-2016
A ball is dropped vertically from a height \(H\) on to a plane surface and permitted to bounce repeatedly along a vertical line. After every bounce, its kinetic energy becomes a quarter of its kinetic energy before the bounce. The ball will come to rest after time
(a)
infinity
(b)
\((2H/g)^{1/2}\)
(c)
\(2(2H/g)^{1/2}\)
(d)
\(3(2H/g)^{1/2}\)
Check Answer
Option d
Q.No:22 TIFR-2016
In a moving car, the wheels will skid if the brakes are applied too suddenly. This is because
(a)
the inertia of the car will carry it forward.
(b)
the momentum of the car must be conserved.
(c)
the impulsive retarding force exceeds the limiting force of static friction.
(d)
the kinetic friction will suddenly get converted to static friction.
Check Answer
Option a
Q.No:23 TIFR-2016
An aircraft, which weighs \(1200 kg\) when unloaded, is on a relief mission, carrying \(4000\) food packets weighing \(1 kg\) each. The plane is gliding horizontally with its engines off at a uniform speed of \(540 kmph\) when the first food packet is dropped. Assume that the horizontal air drag can be neglected and the aircraft keeps moving horizontally. If one food packet is dropped every second, then the distance between the last two packet drops will be
(a)
\(1.5 Km\)
(b)
\(200 m\)
(c)
\(150 m\)
(d)
\(100 m\)
Check Answer
Option c
Q.No:24 TIFR-2016
Imagine that a narrow tunnel is excavated through the Earth as shown in the diagram on the left and that the mass excavated to create the tunnel is extremely small compared to Earth's mass \(M\).

A person falls into the tunnel at one end. at time \(t=0\). Assuming that the tunnel is frictionless, the person will
(a)
fall straight through, escaping Earth's gravity at time \(2\pi \sqrt{R^3/GM}\)
(b)
describe simple harmonic motion with period \(2\pi (d/R) \sqrt{R^3/GM}\)
(c)
describe simple harmonic motion with period \(2\pi \sqrt{(R-d)^3/GM}\)
(d)
describe simple harmonic motion with period \(2\pi \sqrt{R^3/GM}\)
Check Answer
Option d
Q.No:25 TIFR-2016
A uniform solid wheel of mass \(M\) and radius \(r\) is halted at a step of height \(h\) as shown in the figure. The minimum force \(F\), applied horizontally at the centre of the wheel, necessary to raise the wheel over this step is
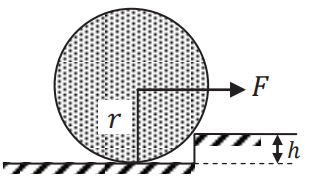
(a)
\(Mg\frac{\sqrt{h(2r-h)}}{r+h}\)
(b)
\(Mg\frac{\sqrt{h(2r+h)}}{r-h}\)
(c)
\(Mg\frac{\sqrt{h(r+h)}}{r-h}\)
(d)
\(Mg\frac{\sqrt{h(2r-h)}}{r-h}\)
Check Answer
Option d
Q.No:26 TIFR-2017
A small elastic ball of mass \(m\) is placed at the apex of a \(45^{\circ}\) inclined plane as shown in the figure below.
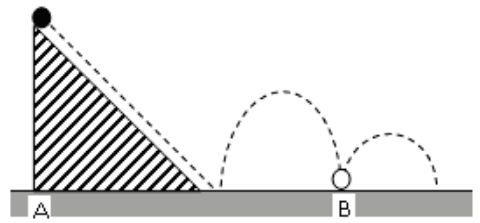
The ball is allowed to slip without friction down the plane (along the dotted line), hit the ground (as shown) and bounce along it. If the height of the inclined plane is \(h\) and the coefficient of restitution between the ball and the ground is \(0.5\), then the distance AB, as marked on the figure, will be
(a)
\(3h\)
(b)
\(2h\)
(c)
\((1+\sqrt{2})h\)
(d)
\(3\sqrt{2}h\)
Check Answer
Option b
Q.No:27 TIFR-2017
A space telescope in orbit around the Earth discovers a new planet, which is observed to move around the Sun by an angle of \(4.72\) milliradians in a year. Assuming a circular orbit, estimate the distance, in A.U., of the planet from the Sun.
Check Answer
Ans 121
Q.No:28 TIFR-2017
In outer space, where the effects of gravity can be neglected, a drop of liquid assumes a spherical shape. However, when disturbed it undergoes shape oscillations (see figure). The frequency \(\nu\) of oscillation of a drop depends on its equilibrium radius, its density and the surface tension.
What would be the numerical value of the ratio \(\nu_{{Hg}}/\nu_{{H_2 O}}\) of the frequencies of oscillation between a drop of mercury (\({Hg}\)) and a drop of water (\({H_2 O}\)) of the same equilibrium radius?
You may use the following data:
You may use the following data:

Check Answer
Ans 0.7
Q.No:29 TIFR-2018
A small block B of mass \(m\) is quickly placed on an inclined plane P, which makes an angle \(\theta\) with a horizontal cart C, on which P is rigidly fixed (see figure). The coefficient of friction between the block B and the plane C is \(\mu\). When the cart stays stationary the block slides down. If the cart C is moving in the horizontal direction with acceleration \(a\), the minimum value of \(a\) for which the block will remain static is
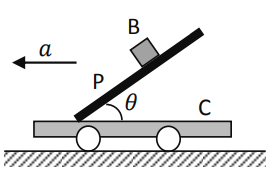
(a)
\(g(\cos{\theta}-\mu\sin{\theta})\)
(b)
\(g\frac{\tan{\theta}-\mu}{\mu\tan{\theta}+1}\)
(c)
\(g\frac{1-\mu\tan{\theta}}{\mu+\tan{\theta}}\)
(d)
\(g(\mu-\sin{\theta}\cos{\theta})\)
Check Answer
Option b
Q.No:30 TIFR-2018
A heavy steel ball is struck by a small steel pellet moving horizontally with velocity \(20 \hspace{1mm}\text{m}\hspace{1mm}\text{s}^{-1}\). If the pellet bounces off the steel ball with no slippage, and then rises vertically to a height \(10 \hspace{1mm}\text{m}\) above the point of contact, then what is \(100\) times the elastic coefficient of restitution (\(e\)) i.e. \(100e\)?
Check Answer
Ans 49
Q.No:31 TIFR-2018
An electron enters a linear accelerator with a speed \(v=10 \hspace{1mm} {m-s}^{-1}\). A vertical section of the accelerator tube is shown in the figure, where the lengths of the successive sections are designed such that the electron takes the same time \(\tau=20 \hspace{1mm}{ms}\) to traverse each section.

If the momentum of the electron increases by \(2\%\) every time it crosses the narrow gap between two sections, what is the length (in {km}) of the collider which will be required to accelerate it to \(100 \hspace{1mm}\text{km-s}^{-1}\)?
Check Answer
Ans 102
Q.No:32 TIFR-2019
A particle of mass \(m\) is placed on an inclined plane making an adjustable angle \(\theta\) with the horizontal, as shown in the figure. The coefficient of friction between the particle and the inclined plane is \(\mu\).
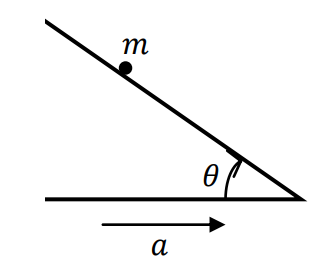
If the inclined plane is moving horizontally with a uniform acceleration \(a<g/\mu\) (see figure), the value of \(\theta\) for which the particle will remain at rest on the plane is
(a)
\(\theta=\tan^{-1}{\left(\frac{\mu g+a}{g+\mu a}\right)}\)
(b)
\(\theta=-\cot^{-1}{\left(\frac{\mu a+g}{a+\mu g}\right)}\)
(c)
\(\theta=\tan^{-1}{\left(\frac{\mu g+a}{g-\mu a}\right)}\)
(d)
\(\theta=\cot^{-1}{\left(\frac{\mu a-g}{a+\mu g}\right)}\)
Check Answer
Option c
Q.No:33 TIFR-2019
A particle of mass \(m\) is bounced on the ground with a velocity \(u\) making an angle of \(\theta\) with the ground. The coefficient of restitution for collisions between the particle and the ground is \(\varepsilon\) and frictional effects are negligible both on the ground and in the air. The horizontal distance travelled by the particle from the point of initial impact till it begins to slide along the ground is

(a)
\(\frac{u^2}{2g}\left(\frac{\varepsilon}{1-\varepsilon}\right)\sin{2\theta}\)
(b)
\(\frac{u^2}{g}\left(\frac{1}{1-\varepsilon}\right)\sin{\theta}\)
(c)
\(\frac{u^2}{g}\left(\frac{\varepsilon}{1-\varepsilon}\right)\tan{2\theta}\)
(d)
\(\frac{u^2}{g}\left(\frac{\varepsilon}{1-\varepsilon}\right)\sin{2\theta}\)
Check Answer
Option d
Q.No:34 TIFR-2019
The three-dimensional object sketched on the right is made by taking a solid sphere of uniform density (shaded) with radius \(R\), and scooping out a spherical cavity (unshaded) as shown, which has diameter \(R\).

If this object has mass \(M\), its moment of inertia about the tangential axis passing through the point where the spheres touch (as shown in the figure) is
(a)
\(\frac{3}{16}MR^2\)
(b)
\(\frac{62}{35}MR^2\)
(c)
\(\frac{31}{70}MR^2\)
(d)
\(\frac{31}{20}MR^2\)
Check Answer
Option d
Q.No:35 TIFR-2019
Consider a sphere of radius \(R\), with the north pole \(N\) marked as shown in the figure below.
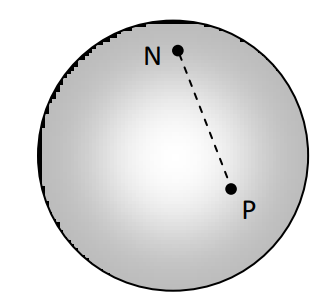
The r.m.s. distance (straight line cutting through the sphere) of a point \(P\) on the sphere from this north pole \(N\) is given by
(a)
\(R\)
(b)
\(2\sqrt{2/5}R\)
(c)
\(\sqrt{4\pi}R\)
(d)
\(\sqrt{2}R\)
Check Answer
Option d
Q.No:36 TIFR-2020
Consider a satellite orbiting the Earth in a circular orbit, as sketched in the figure on the right (not to scale). The satellite has four small thruster rockets, whose exhaust gases come out along
(A)
the forward direction,
(B)
the backward direction,
(C)
radially inward towards the Earth's centre, and
(D)
radially outward from the Earth's centre,
as indicated in the figure.
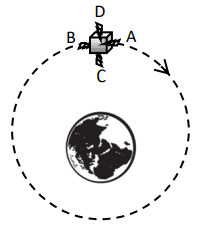
If the satellite wants to increase its speed, while remaining in a circular orbit, and has fuel enough to keep only one thruster rocket in operation, it should fire the rocket marked
(a)
\(A\)
(b)
\(B\)
(c)
\(C\)
(d)
\(D\)
Check Answer
Option d
Q.No:37 TIFR-2020
Consider two planets \(P_1\) and \(P_2\) which can be modeled as uniform spheres of radii \(R_1\) and \(R_2\) respectively, and of the same material with the same density and other physical properties. If the maximum possible height of a conical mountain (of the same material) on these planets is denoted by \(h_1\) and \(h_2\) respectively (\(h_1\ll R_1, h_2\ll R_2\)), then the ratio \(h_1/h_2\) is
(a)
\(R_2/R_1\)
(b)
\(R_1/R_2\)
(c)
\(R_2^{2/3}/R_1^{2/3}\)
(d)
\(R_1^{2/3}/R_2^{2/3}\)
Check Answer
Option a
Q.No:38 TIFR-2020
A roundabout whose rotating base is a heavy uniform disc of radius \(2 \hspace{1mm}\text{m}\) and mass \(400 \hspace{1mm}\text{kg}\) has a central pillar and handles which are of negligible mass (see figure). The roundabout is set rotating at a steady rate of \(20\) r.p.m.

Four small children, of mass \(10 \hspace{1mm}\text{kg}, 20 \hspace{1mm}\text{kg}, 30 \hspace{1mm}\text{kg}\) and \(40 \hspace{1mm}\text{kg}\) respectively, step gently on to the edge of the roundabout, each with velocity \(7.2 \hspace{1mm}\text{km}/\text{hr}\) along a tangential direction and cling to the handles. After holding on for some time, the children step gently off the roundabout with the same velocity, but this time in a radial direction.
Neglecting all effects of friction and air drag, the final rate of rotation of the roundabout will be about
(a)
\(28\) r.p.m.
(b)
\(25\) r.p.m.
(c)
\(36\) r.p.m.
(d)
\(21\) r.p.m.
Check Answer
Option b
Q.No:39 TIFR-2021
A body is dropped from rest at a height \(h\) above the surface of the Earth at a latitude \(\lambda_N\) in the northern hemisphere. If the angular velocity of rotation of the Earth is \(\omega\), the lateral displacement of the body at its point of impact on the Earth's surface will be
(a)
\(\left(\frac{8h^3\omega^2}{9g}\right)^{1/2} \cos{\lambda_N}\)
(b)
\(\left(\frac{8h^3\omega^2}{9g}\right)^{1/2} \sin{\lambda_N}\)
(c)
\(\left(\frac{2h^3\omega^2}{9g}\right)^{1/2} \cos{\lambda_N}\)
(d)
\(\left(\frac{2h^3\omega^2}{9g}\right)^{1/2} \sin{\lambda_N}\)
Check Answer
Option a
Q.No:40 TIFR-2021
A stick \(S\) of uniform density of mass \(M\), length \(L\), and negligible width, is constrained to move such that its two ends always stay on the inside of a fixed vertical, circular ring of inner radius \(R\), as shown below.
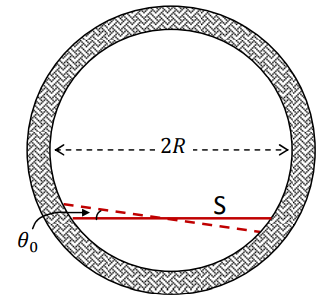
If the stick \(S\) is displaced by a small angle \(\theta_0\) from its equilibrium position and then allowed to oscillate freely, the angular frequency \(\omega\) of oscillations will be
[Ignore the friction between the stick and the ring.]
(a)
\(\left(\frac{6g}{6R^2-L^2}\right)^{1/2}\left(R^2-\frac{L^2}{4}\right)^{1/4}\)
(b)
\(\left(\frac{4g}{6R^2-L^2}\right)^{1/2}\left(R^2-\frac{L^2}{4}\right)^{1/4}\)
(c)
\(\left(\frac{6g}{3R^2-L^2}\right)^{1/2}\left(R^2-\frac{L^2}{4}\right)^{1/4}\)
(d)
\(\left(\frac{4g}{2R^2-L^2}\right)^{1/2}\left(R^2-\frac{L^2}{4}\right)^{1/4}\)
Check Answer
Option a
Q.No:41 TIFR-2022
A solid homogeneous sphere floats in water with a portion sticking out above the water, as shown in the figure below. The height of the highest point above the water surface is \(R/2\) where \(R\) is the radius of the
sphere.
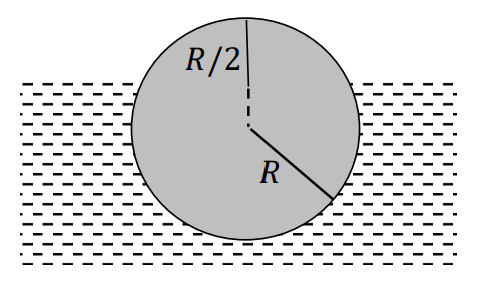
If the density of water is 1 g c\(m^{-3}\), the density of the
material (in g c\(m^{-3}\)) must be
(a)
\(27/32\)
(n)
\(5/32\)
(c)
\(13/18\)
(d)
\(5/18\)
Check Answer
Option a
Q.No:42 TIFR-2022
A hollow metal sphere filled with a thick, highly viscous oil is rotating about a vertical axis with an initial angular velocity \(\omega_0\). However, there is a small hole at the bottom of this sphere, through which drops of oil are leaking out vertically at a steady rate. The
variation of the angular velocity \(\omega(t)\) of the sphere with time \(t\) is best represented graphically by

Check Answer
Option a
Q.No:43 TIFR-2022
A pendulum which is suspended from the ceiling of a train has time period \(T_0\) when the train is stationary. When the train moves with a small but steady speed \(v\) around a horizontal circular track of radius \(R\), the time period of the pendulum will be
(a)
\(T_0 \hspace{0.5mm} (1-\frac{v^2 T_0^2 }{4 \pi^2 R})^{-1/2}\)
(b)
\(T_0 \hspace{0.5mm} (1+\frac{v^2 T_0^2 }{4 \pi^2 R})^{-1/2}\)
(c)
\(T_0 \hspace{0.5mm} (1-\frac{v^4 }{g^2 R})^{1/4}\)
(d)
\(T_0 \hspace{0.5mm} (1+\frac{v^4 }{g^2 R})^{1/4}\)
Check Answer
Option a
Q.No:44 TIFR-2022
A cricket ball, bowled by a fast bowler, rises from the pitch at an angle of 300 with a speed of 72 km/hr, then moves straight ahead and, at a height of 0.5 m, strikes the flat surface of the bat held firmly at rest in a horizontal position (see figure). As a result, the ball bounces off elastically, providing a return catch straight back to the bowler.

If the coefficient of restitution between the bat and the ball is 0.577, the acceleration due to gravity is 10 m \(s^{-2}\) and air resistance can be neglected, the catch will carry, before hitting the ground, to a distance of approximately
(a)
19.5 m
(b)
37.0 m
(c)
9.5 m
(d)
21.0 m
Check Answer
Option a
Q.No:45 TIFR-2022
A dumbbell consists of two small spherical masses \(M\) each, connected by a thin massless rod of length \(2\ell\)
This dumbbell is centred at the origin, and is rotating about the z-axis with a uniform angular velocity \(\omega\), making an angle \(\theta\) with the z-axis (see figure).
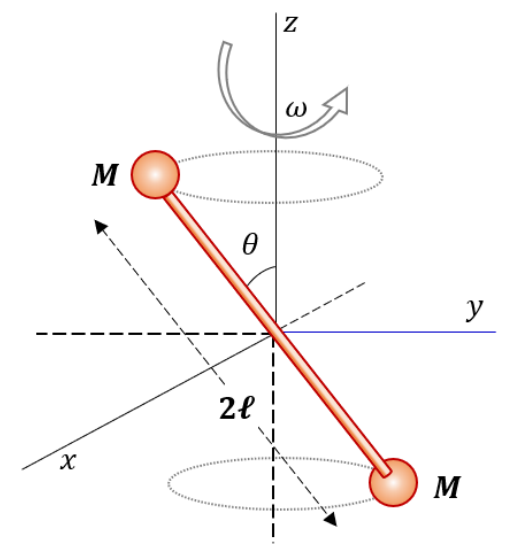
Neglecting effects due to gravity, at the instant when the dumbbell is wholly in the yz-plane (as shown in the figure), the magnitude of torque
about the origin will be
(a)
\(M \hspace{0.3mm} \ell^2 \hspace{0.3mm} \omega^2 \hspace{0.3mm}sin \hspace{0.3mm} 2\theta \)
(b)
\(2M \hspace{0.3mm} \ell^2 \hspace{0.3mm} \omega^2 \hspace{0.3mm}sin^2 \hspace{0.3mm} \theta \)
(c)
\(2M \hspace{0.3mm} \ell^2 \hspace{0.3mm} \omega^2 \hspace{0.3mm} cos^2 \hspace{0.3mm} \theta \)
(d)
zero
Check Answer
Option a
Q.No:46 TIFR-2023
A small body of mass \(m\) is released from rest at the top of a frictionless curved surface as shown in the figure., and permitted to slide down the curve. At the end point \(C\), the tangent to the curve is horizontal. The mass then falls on the ground at a distance \(d\) as shown in the figure below when the experiment is carried out on the surface of the Earth. The heights \(h_1\) and \(h_2\) are also shown in the figure.

Suppose the same experiment is repeated on the Moon, where the acceleration due to gravity is \(g'=g/6\), where \(g\) is the value on Earth. The corresponding distance \(d'\) at which the mass will fall on the ground in the Moon is
(a)
\(6d\)
(b)
dependent on the shape of the curve
(c)
\(d\sqrt{h_1/h_2}\)
(d)
\(d\)
Check Answer
Option d
Q.No:47 TIFR-2023
A particle is executing simple harmonic motion in a straight line. When the distance of the particle from the equilibrium position is \(x_1\) and \(x_2\), the corresponding values of its velocity are \(v_1\) and \(v_2\) respectively. The time period of oscillation is given by
(a)
\(2\pi \sqrt{\frac{x_2 ^2-x_1 ^2}{v_2 ^2- v_1 ^2}}\)
(b)
\(2\pi \frac{x_2 -x_1 }{v_2 - v_1 }\)
(c)
\(2\pi \frac{x_2 -x_1 }{v_1 - v_2 }\)
(d)
\(2\pi \sqrt{\frac{x_2 ^2-x_1 ^2}{v_1 ^2- v_2 ^2}}\)
Check Answer
Option a
Q.No:48 TIFR-2023
A solid cylinder of uniform mass density rolls down a fixed inclined plane without slipping (see figure).

The fraction of the total kinetic energy of the cylinder associated with its rotation about its centre of mass is
(c)
\(1/6\)
(c)
\(1/2\)
(c)
\(1/4\)
(c)
\(1/3\)
Check Answer
Option d
Q.No:49 TIFR-2023
A thin equilateral triangular plate of uniform mass density is attached to a fixed horizontal support along one of its sides through a frictionless hinge, as shown in the figure below. The vertical distance between the rod and the lower tip of the plate is \(h\).
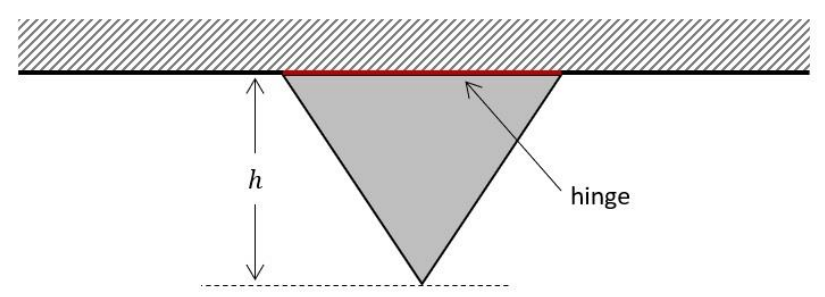
If the pointed tip of the plate is displaced (out of the plane of the paper) so that its plane forms a small angle with the vertical plane passing through the rod, the angular frequency \(\omega\) of the resultant motion is \(\omega\) =
(a)
\(\sqrt{\frac{2g}{h}}\)
(b)
\(\sqrt{\frac{2 \sqrt{3} g}{h}}\)
(c)
\(\sqrt{\frac{2g}{\sqrt{3}h}}\)
(d)
\(\sqrt{\frac{ \sqrt{3} g}{2 h}}\)
Check Answer
Option a
Q.No:50 TIFR-2023
A simple pendulum is oscillating freely in the vertical plane. If the string is shortened, the angular amplitude \(\theta_{max}\) will change by a factor
(a)
2
(b)
Does not change
(c)
\(\sqrt{2}\)
(d)
\(2^{3/4}\)
Check Answer
Option d
Q.No:51 TIFR-2024
A horizontal constant force \( F \) is applied on a uniform disc placed on a horizontal surface. The mass of the disc is \( m \), and the radius is \( r \). The point of application of \( F \) is at a height \( h (< 2r) \) from the surface. The disc starts from rest at \( t = 0 \) and rolls without slipping. What is the speed of the centre of the disc at time \( t \)?

(a) \( \frac{2Fht}{3mr} \)
(b) \( \frac{Ft}{m} \)
(c) \( \frac{2Ft}{3m} \)
(d) \( \frac{3Fht}{2mr} \)
Check Answer
Option a
Q.No:52 TIFR-2024
Two equal masses \( m \) are connected with a massless string. The first mass is initially set in a uniform circular motion with speed \( v_i \), at a radius \( r_i \) on top of a table while the second mass hangs vertically on the string which passes through a hole in the center of the table (C), as shown in the figure below.
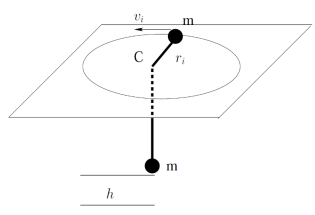
The system is released with this initial configuration and the second mass starts falling. What is the net speed of the first mass when the second mass has fallen a height \( h \) (smaller than \( r_i \))?
(Assume that there is no friction and that the string always remains tight.)
(a) \( \sqrt{gh + \frac{1}{2} v_i^2 \left[ 1 + \left( \frac{r_i^2}{(r_i - h)^2} \right) \right]} \)
(b) \( \sqrt{gh + \frac{1}{2} v_i^2 \left[ 1 + \frac{r_i}{(r_i - h)} \right]} \)
(c) \( \sqrt{gh + \frac{1}{2} v_i^2 \left[ 1 + \left( \frac{(r_i - h)^2}{r_i^2} \right) \right]} \)
(d) \( \sqrt{gh + \frac{1}{2} v_i^2 \left[ 1 + \frac{(r_i - h)}{r_i} \right]} \)
Check Answer
Option a
Q.No:53 TIFR-2024
A frictionless disk of mass \( m \) is balanced at rest on the edges of two platforms at points \( A \) and \( B \) that are at equal height as shown below. The angle made by the line joining the centre to point \( A \) (line \( CA \)) with the vertical is \( \pi/3 \).

What is the magnitude of the force exerted by point \( A \) on the disk?
(a) \( mg \)
(b) \( \frac{mg}{2} \)
(c) \( \frac{mg}{\sqrt{3}} \)
(d) \( \frac{mg\sqrt{3}}{2} \)
Check Answer
Option a
Q.No:54 TIFR-2025
Water flows out through a small horizontal opening of area \(A\) at the bottom of a tank
of height \(H\). The flow is laminar and driven by gravity.
What is the area \(A'\) of the stream transverse to the fluid velocity at a point located
a vertical distance \(h\) below the opening?
Assume:
• Atmospheric pressure is negligible
• Dissipation effects are negligible
• The thickness of the stream is negligible compared to \(H\) and \(h\)
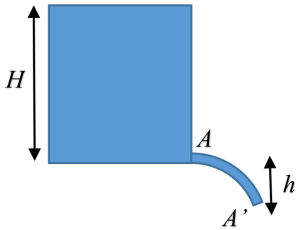
a) \(A \sqrt{\frac{H}{H + h}}\)
b) \(A \frac{H}{H + h}\)
c) \(A \left(1 + \frac{h}{H}\right)\)
d) \(A \sqrt{\frac{H}{H + h}}\)
Check Answer
Option a
Q.No:55 TIFR-2025
A massless string of total length \(L\) has one end fixed to the ceiling at point \(P\).
The string is initially completely wrapped around a solid uniform disk of radius \(R\)
(with \(R \ll L\)) and mass \(m\).
The disk is released from rest at time \(t = 0\) and falls vertically under gravity.
As it falls, the string unwinds from the disk and always remains taut.
What is the velocity of the disk at time \(t\), before the string is completely unwound?

a) \(-\frac{2gt}{3}\,\hat{y}\)
b) \(-gt\,\hat{y}\)
c) \(-\frac{3gt}{4}\,\hat{y}\)
d) \(-\frac{2gt}{3}\,\hat{y}\)
Check Answer
Option a
Q.No:56 TIFR-2025
A ball \(A\) is dropped from a height \(h\) onto the floor.
On the first bounce, it rises to a height \(h/4\).
Now two identical balls \(A\) and \(B\) are dropped together from the same height \(h\),
with ball \(B\) directly above ball \(A\), as shown in the figure.
Assume:
• The coefficient of restitution between balls \(A\) and \(B\) is 1
• Sizes of the balls and their initial separation are negligible
How high does ball \(B\) rise on its first bounce?

a) \(h/4\)
b) \(h\)
c) \(h/2\)
d) \(h/8\)
