Q.No:1 CSIR Dec-2014
A ladder rests against a wall as shown. The top and the bottom ends of the ladder are marked A and B. The base B slips. The central point C of the ladder falls along

(1)
a parabola
(2)
the arc of a circle
(3)
a straight line
(4)
a hyperbola
Check Answer
Option 2
Q.No:2 CSIR Dec-2014
The radius of Earth is approximately \(6400 km\). The height \(h\) at which the acceleration due to Earth's gravity differs from \(g\) at the Earth's surface by approximately \(1\%\) is
(1)
\(64 km\)
(2)
\(48 km\)
(3)
\(32 km\)
(4)
\(16 km\)
Check Answer
Option 3
Q.No:3 CSIR Dec-2014
The pressure \(P\) of a fluid is related to its number density \(\rho\) by the equation of state
\[
P=a\rho+b\rho^2
\]
where \(a\) and \(b\) are constants. If the initial volume of the fluid is \(V_0\), the work done on the system when it is compressed so as to increase the number density from an initial value of \(\rho_0\) to \(2\rho_0\) is
(1)
\(a\rho_0 V_0\)
(2)
\((a+b\rho_0)\rho_0 V_0\)
(3)
\(\left(\frac{3a}{2}+\frac{7\rho_0 b}{3}\right)\rho_0 V_0\)
(4)
\((a\ln{2}+b\rho_0)\rho_0 V_0\)
Check Answer
Option 4
Q.No:4 CSIR Dec-2014
The probe Mangalyaan was sent recently to explore the planet Mars. The inter-planetary part of the trajectory is approximately a half-ellipse with the Earth (at the time of launch), Sun and Mars (at the time the probe reaches the destination) forming the major axis. Assuming that the orbits of Earth and Mars are approximately circuit with radii \(R_E\) and \(R_M\), respectively, the velocity (with respect to the Sun) of the probe during its voyage when it is at a distance \(r\) (\(R_E\ll r\ll R_M\)) from the Sun, neglecting the effect of Earth and Mars, is

(1)
\(\sqrt{2GM\frac{(R_E+R_M)}{r(R_E+R_M-r)}}\)
(2)
\(\sqrt{2GM\frac{(R_E+R_M-r)}{r(R_E+R_M)}}\)
(3)
\(\sqrt{2GM\frac{R_E}{rR_M}}\)
(4)
\(\sqrt{\frac{2GM}{r}}\)
Check Answer
Option 2
Q.No:5 CSIR June-2015
A particle moves in two dimensions on the
ellipse \(x^2 + 4y^2 = 8\). At a particular instant it is at the point (x,y) = (2,1) and the x-component of its velocity is 6 (in suitable units). Then the y-component of its velocity is
(1)
\(-3\)
(2)
\(-2\)
(3)
1
(4)
4
Check Answer
Option 1
Q.No:6 CSIR Dec-2015
Two masses, \(m\) each, are placed at the points \((x, y)=(a, a)\) and \((-a, -a)\). Two masses, \(2m\) each, are placed at the points \((a, -a)\) and \((-a, a)\). The principal moments of inertia of the system are
(1)
\(2ma^2, 4ma^2\)
(2)
\(4ma^2, 8ma^2\)
(3)
\(4ma^2, 4ma^2\)
(4)
\(8ma^2, 8ma^2\)
Check Answer
Option 2
Q.No:7 CSIR June-2016
A ball of mass \(m\), initially at rest, is dropped from a height of \(5\) meters. If the coefficient of restitution is \(0.9\), the speed of the ball just before it hits the floor the second time is approximately (take \(g=9.8 m/s^2\))
(1)
\(9.80 m/s\)
(2)
\(9.10 m/s\)
(3)
\(8.91 m/s\)
(4)
\(7.02 m/s\)
Check Answer
Option 3
Q.No:8 CSIR Dec-2016
After a perfectly elastic collision of two identical balls, one of which was initially at rest, the velocities of both the balls are non-zero. The angle \(\theta\) between the final velocities (in the lab frame) is
(1)
\(\theta=\frac{\pi}{2}\)
(2)
\(\theta=\pi\)
(3)
\(0< \theta\leq \frac{\pi}{2}\)
(4)
\(\frac{\pi}{2}< \theta\leq \pi\)
Check Answer
Option 1
Q.No:9 CSIR June-2017
A ball weighing \(100 gm\), released from a height of \(5 m\), bounces perfectly elastically off a plate. The collision time between the ball and the plate is \(0.5 s\). The average force on the plate is approximately
(1)
\(3 N\)
(2)
\(2 N\)
(3)
\(5 N\)
(4)
\(4 N\)
Check Answer
Option 3
Q.No:10 CSIR Dec-2017
A disc of mass \(m\) is free to rotate in a plane parallel to the \(xy\) plane with an angular velocity \(-\omega \hat{z}\) about a massless rigid rod suspended from the roof of a stationary car (as shown in the figure below). The rod is free to orient itself along any direction.
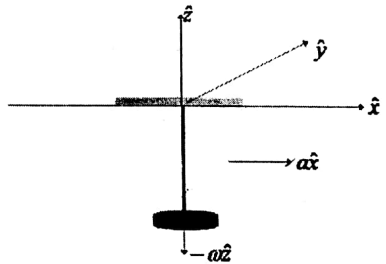
The car accelerates in the positive \(x\)-direction with an acceleration \(a>0\). Which of the following statements is true for the coordinates of the centre of mass of the disc in the reference frame of the car?
(1)
only the \(x\) and the \(z\) coordinates change
(2)
only the \(y\) and the \(z\) coordinates change
(3)
only the \(x\) and the \(y\) coordinates change
(4)
all the three coordinates change
Check Answer
Option 4
Q.No:11 CSIR Dec-2017
A cyclist, weighing a total of \(80 kg\) with the bicycle, pedals at a speed of \(10 m/s\). She stops pedalling at an instant which is taken to be \(t=0\). Due to the velocity dependent frictional force, her velocity is found to vary as \(v(t)=10/\left(1+\frac{t}{30}\right) m/s\), where \(t\) is measured in seconds. When the velocity drops to \(8 m/s\), she starts pedalling again to maintain a constant speed. The energy expended by her in \(1\) minute at this (new) speed, is
(1)
\(4 kJ\)
(2)
\(8 kJ\)
(3)
\(16 kJ\)
(4)
\(32 kJ\)
Check Answer
Option 2
Q.No:12 CSIR Dec-2017
The spring constant \(k\), of a spring of mass \(m_s\), is determined experimentally by loading he spring with mass \(M\) and recording the time period \(T\), for a single oscillation. If the experiment is carried out for different masses, then the graph that correctly represents the result is
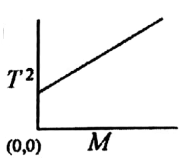
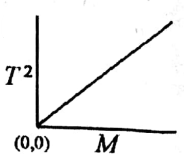
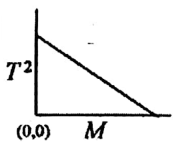
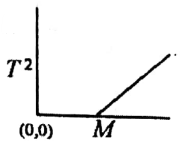
Check Answer
Option 1
Q.No:13 CSIR June-2019
An object is dropped on a cushion from a height \(10 m\) above it. On being hit, the cushion is depressed by \(0.1 m\). Assuming that the cushion provides a constant resistive force, the deceleration of the object after hitting the cushion, in terms of the acceleration due to gravity \(g\), is
(1)
\(10g\)
(2)
\(50g\)
(3)
\(100g\)
(4)
\(g\)
Check Answer
Option 3
Q.No:14 CSIR June-2019
A turn-table is rotating with a constant angular velocity \(\omega_0\). In the rotating frame fixed to the turntable, a particle moves radially outwards at a constant speed \(v_0\). The acceleration of the particle in the \(r\theta\)-coordinates, as seen from an inertial frame, the origin of which is at the centre of the turntable, is
(1)
\(-r\omega_0^2 \hat{r}\)
(2)
\(2r\omega_0^2 \hat{r}+v_0 \omega_0 \hat{\theta}\)
(3)
\(r\omega_0^2 \hat{r}+2v_0 \omega_0 \hat{\theta}\)
(4)
\(-r\omega_0^2 \hat{r}+2v_0 \omega_0 \hat{\theta}\)
Check Answer
Option 4
Q.No:15 CSIR June-2019
A solid spherical cork of radius \(R\) and specific gravity \(0.5\) floats on water. The cork is pushed down so that its centre of mass is at a distance \(h\) (where \(0< h< R\)) below the surface of water, and then released. The volume of the part of the cork above water level is \(\pi R^3\left(\frac{2}{3}-\cos{\theta_0}+\frac{1}{3}\cos^3{\theta_0}\right)\), where \(\theta_0\) is the angle as shown in the figure.
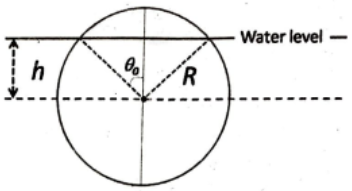
At the moment of release, the dependence of the upward force on the cork on \(h\) is
(1)
\(\frac{h}{R}-\frac{1}{3}\left(\frac{h}{R}\right)^3\)
(2)
\(\frac{h}{R}+\frac{1}{3}\left(\frac{h}{R}\right)^3\)
(3)
\(\frac{h}{R}-\frac{2}{3}\left(\frac{h}{R}\right)^3\)
(4)
\(\frac{h}{R}+\frac{2}{3}\left(\frac{h}{R}\right)^3\)
Check Answer
Option 1
Q.No:16 CSIR Dec-2019
A ball, initially at rest, is dropped from a height \(h\) above the floor bounces again and again vertically. If the coefficient of restitution between the ball and the floor is \(0.5\), the total distance travelled by the ball before it comes to rest is
(1)
\(8h/3\)
(2)
\(5h/3\)
(3)
\(3h\)
(4)
\(2h\)
Check Answer
Option 2
Q.No:17 Assam CSIR Dec-2019
A solid ball on a horizontal surface, initially at rest, starts to slide with an initial velocity \(u\) when it is given a horizontal impulse along an axis passing through its centre. If the coefficient of sliding friction is zero, then the time (measured from the time of impulse) when the ball will start to roll, is
(1)
\(0\) (it will roll immediately)
(2)
\(\frac{2}{7} \frac{u}{g}\)
(3)
\(\frac{2}{5} \frac{u}{g}\)
(4)
\(\infty\) (it will never roll)
Check Answer
Option 4
Q.No:18 Assam CSIR Dec-2019
A solid metal cylinder, of radius \(R\) and height \(4R\), is resting on its base on a horizontal table. When the cylinder is tilted on one of its edges, the variation of its potential energy \(V(\theta)\), as a function of the tilt angle \(\theta\), is qualitatively best represented by which of the following figures?




Check Answer
Option 3
Q.No:19 Assam CSIR Dec-2019
Two coplanar identical rings, each of mass \(M\) and radius \(R\), are connected such that the centre of each ring falls on the circumference of the other. The moment of inertia of the system about an axis passing through its centre of mass and perpendicular to the plane of the rings, is
(1)
\(2MR^2\)
(2)
\(\frac{7}{2}MR^2\)
(3)
\(\frac{5}{2}MR^2\)
(4)
\(4MR^2\)
Check Answer
Option 3
Q.No:20 CSIR June-2020
A frictionless horizontal circular table is spinning with a uniform angular velocity \(\omega\) about the vertical axis through its centre. If a ball of radius \(a\) is placed on it at a distance \(r\) from the centre of the table, its linear velocity will be
(a)
\(-r\omega \hat{r}+a\omega \hat{\theta}\)
(b)
\(r\omega \hat{r}+a\omega \hat{\theta}\)
(c)
\(a\omega \hat{r}+r\omega \hat{\theta}\)
(d)
\(0\) (zero)
Check Answer
Option d
Q.No:21 CSIR June-2020
Falling drops of rain break up and coalesce with each other and finally achieve an approximately spherical shape in the steady state. The radius of such a drop scales with the surface tension \(\sigma\) as
(a)
\(1/\sqrt{\sigma}\)
(b)
\(\sqrt{\sigma}\)
(c)
\(\sigma\)
(d)
\(\sigma^2\)
Check Answer
Option a
Q.No:22 CSIR June-2020
The velocity \(\nu(x)\) of a particle moving in one dimension is given by \(\nu(x)=\nu_0\sin{\left(\frac{\pi x}{x_0}\right)}\), where \(\nu_0\) and \(x_0\) are positive constants of appropriate dimensions. If the particle is initially at \(x/x_0=\in\), where \(|\in|\ll 1\), then, in the long time, it
(a)
Executes an oscillatory motion around \(x=0\)
(b)
Tends towards \(x=0\)
(c)
Tends towards \(x=x_0\)
(d)
Executes an oscillatory motion around \(x=x_0\)
Check Answer
Option c
Q.No:23 CSIR Feb-2022
A particle of mass m moves in a potential that is \(V=\frac{1}{2}m(\omega_1^2x^2+\omega_2^2y^2+\omega_3^2z^2)\) in the
coordinates of a non-inertial frame \(F\) . The frame \(F\) is rotating with respect to an inertial frame
with an angular velocity \(\hat{k}\Omega\) , where \(\hat{k}\) it is the unit vector along their common z -axis. The
motion of the particle is unstable for all angular frequencies satisfying
(1)
\((\Omega^2-\omega_1^2)(\Omega^2-\omega_2^2)>0\)
(2)
\((\Omega^2-\omega_1^2)(\Omega^2-\omega_2^2)<0\)
(3)
\((\Omega^2-(\omega_1+\omega_2)^2)(\Omega^2-|\omega_1-\omega_2|^2)>0\)
(4)
\((\Omega^2-(\omega_1+\omega_2)^2)(\Omega^2-|\omega_1-\omega_2|^2)<0\)
Check Answer
Option 2
Q.No:24 CSIR Sep-2022
The periods of oscillation of a simple pendulum at the sea level and at the top of a mountain of height 6 km are \(T_1\) and \(T_2\) respectively. If the radius of the earth is approximately 6000 km, then \(\frac{(T_1-T_2)}{T_1}\) is closest to
(1)
\(-10^{-4}\)
(2)
\(-10^{-3}\)
(3)
\(10^{-4}\)
(4)
\(10^{-3}\)
Check Answer
Option 4
Q.No:25 CSIR Sep-2022
A wire, connected to a massless spring of spring constant \(k\) and a block of mass \(m\),goes around a disc of radius \(a\) and moment of inertia \(I\), as shown in the figure.
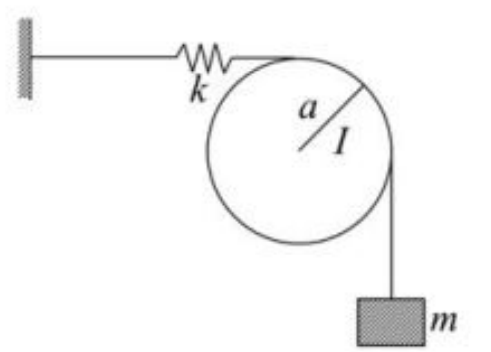
Assume that the spring remains horizontal, the pulley rotates freely and there is no slippage between the wire and the pulley. The angular frequency of small oscillations of the disc is
(1)
\(\sqrt{\frac{2ka^2}{ma^2+I}}\)
(2)
\(\sqrt{\frac{ka^2}{ma^2+I}}\)
(3)
\(\sqrt{\frac{ka^2}{ma^2+2I}}\)
(4)
\(\sqrt{\frac{2ka^2}{ma^2+I}}\)
Check Answer
Option 2
Q.No:26 CSIR Sep-2022
Earth may be assumed to be an axially symmetric freely rotating rigid body. The ratio of the principal moments of
inertia about the axis of symmetry and an axis perpendicular to it is 33:32. If \(T_0\) is the time taken by earth to make one rotation around its axis of symmetry, then the time period of precession is closest to
(1)
\(33T_0\)
(2)
\(33T_0/2\)
(3)
\(32 T_0\)
(4)
\(16T_0\)
Check Answer
Option 3
Q.No:27 CSIR June-2023
A uniform circular disc on the \(xy\)-plane with its centre at the origin has a moment of inertia \(I_0\) about the \(x\)-axis. If the disc is set in rotation about the origin with an angular velocity \(\omega=\omega_0(\hat{j}+\hat{k})\), the direction of its angular momentum is along
1) \(-\hat{i}+\hat{j}+\hat{k}\)
2) \(-\hat{i}+\hat{j}+2\hat{k}\)
3) \(\hat{j}+2\hat{k}\)
4) \(\hat{j}+\hat{k}\)
Check Answer
Option 3
Q.No:28 CSIR June-2024
A uniform plane square sheet of mass \( m \) is centered at the origin of an inertial frame. The sheet is rotating about an axis passing through the origin. At an instant when all its vertices lie on \( x \) and \( y \) axes, the angular momentum is \( \vec{L} = I_0 \omega_0 (2\hat{i} + \hat{j} + 2\hat{k}) \), where \( I_0 \) is the moment of inertia about the \( x \) axis. At this instant, the angular velocity of the sheet is:
1) \((2\hat{i} + \hat{j} + 2\hat{k})\omega_0\)
2) \((2\hat{i} + \hat{j} + \hat{k})\omega_0\)
3) \((2\hat{i} + \hat{j})\omega_0\)
4) \((\hat{i} + \hat{j})\omega_0\)
Check Answer
Option 2
Q.No:29 CSIR Dec-2024
Two blocks \(m_1\) and \(m_2\) are in contact on a frictionless horizontal table.
A horizontal force \(F\) is applied to one of the blocks, as shown in the figure.
If \(m_1 = 2\,\mathrm{kg}\), \(m_2 = 1\,\mathrm{kg}\), and \(F = 3\,\mathrm{N}\),
what is the force of contact between the blocks?

1) \(1\,\mathrm{N}\)
2) \(2\,\mathrm{N}\)
3) \(1.5\,\mathrm{N}\)
4) \(3\,\mathrm{N}\)
Check Answer
Option 1
Q.No:1 GATE-2012
Two uniform thin rods of equal length, \(L\), and masses \(M_1\) and \(M_2\) are joined together along the length. The moment of inertia of the combined rod of length \(2L\) about an axis passing through the mid-point and perpendicular to the length of the rod is,
(A)
\((M_1+M_2)\frac{L^2}{12}\)
(B)
\((M_1+M_2)\frac{L^2}{6}\)
(C)
\((M_1+M_2)\frac{L^2}{3}\)
(D)
\((M_1+M_2)\frac{L^2}{2}\)
Check Answer
Option C
Q.No:2 GATE-2013
A uniform circular disk of radius \(R\) and mass \(M\) is rotating with angular speed \(\omega\) about an axis, passing through its center and inclined at an angle \(60\) degrees with respect to its symmetry axis. The magnitude of the angular momentum of the disk is,
(A)
\(\frac{\sqrt{3}}{4} \omega MR^2\)
(B)
\(\frac{\sqrt{3}}{8} \omega MR^2\)
(C)
\(\frac{\sqrt{7}}{8} \omega MR^2\)
(D)
\(\frac{\sqrt{7}}{4} \omega MR^2\)
Check Answer
Option C
Q.No:3 GATE-2017
A uniform solid cylinder is released on a horizontal surface with speed \(5 m/s\) without any rotation (slipping without rolling). The cylinder eventually starts rolling without slipping. If the mass and radius of the cylinder are \(10 gm\) and \(1 cm\) respectively, the final linear velocity of the cylinder is _____________________ \(m/s\). (up to two decimal places).
Check Answer
Ans 3.30-3.35
Q.No:4 GATE-2017
A person weighs \(w_p\) at Earth's north pole and \(w_e\) at the equator. Treating the Earth as a perfect sphere of radius \(6400 km\), the value \(100\times (w_p-w_e)/w_p\) is ______. (up to two decimal places). (Take \(g=10 ms^{-2}\)).
Check Answer
Ans 0.32-0.36
Q.No:5 GATE-2018
A uniform circular disc of mass \(m\) and radius \(R\) is rotating with angular speed \(\omega\) about an axis passing through its center and making an angle \(\theta=30^{\circ}\) with the axis of the disc. If the kinetic energy of the disc is \(\alpha m\omega^2 R^2\), the value of \(\alpha\) is ___________ (up to \(2\) decimal places).
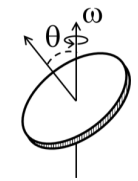
Check Answer
Ans 0.21-0.23
Q.No:6 GATE-2023
A symmetric top has principal moments of inertia \(I_1=I_2=\frac{2\alpha}{3}, I_3=2\alpha\) about a set of principal axes 1, 2, 3 respectively, passing through its center of mass, where \(\alpha\) is a positive constant. There is no force acting on the body and the angular speed of the body about the 3-axis is \(\omega_3=\frac{1}{8}\) rad/s. With what
angular frequency in rad/s does the angular velocity vector \(\vec{\omega}_1\) precess about the 3-axis?
(A)
2
(B)
3
(C)
5
(D)
7
Check Answer
Option A
Q.No:7 GATE-2025
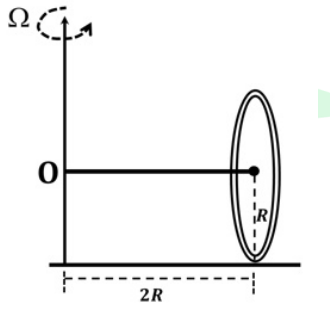
A wheel of mass \(4M\) and radius \(R\) is made of a thin uniform distribution of mass \(3M\)
at the rim and a point mass \(M\) at the center. The spokes of the wheel are massless.
The center of mass of the wheel is connected to a horizontal massless rod of length \(2R\),
with one end fixed at \(O\), as shown in the figure. The wheel rolls without slipping on
horizontal ground with angular speed \(\Omega\).
If \(\vec{L}\) is the total angular momentum of the wheel about \(O\), then the magnitude
\[
\left|\frac{d\vec{L}}{dt}\right| = N \left(M R^{2} \Omega^{2}\right).
\]
The value of \(N\) (an integer) is _____.