Q.No:1 JAM-2015
Consider the coordinate transformation \(x'=\frac{x+y}{\sqrt{2}}, y'=\frac{x-y}{\sqrt{2}}\). The relation between the area elements
\(dx'dy'\) and \(dxdy\) is given by \(dx'dy'=J\hspace{0.5mm}dxdy\). The value of \(J\) is
(A)
\(2\)
(B)
\(1\)
(C)
\(-1\)
(D)
\(-2\)
Check Answer
Option C
Q.No:2 JAM-2016
Consider a function \(f(x,y)=x^3+y^3\), where \(y\) represents a parabolic curve \(x^2+1\). The total derivative of \(f\) with respect to \(x\), at \(x=1\) is ___________.
Check Answer
Ans 27
Q.No:3 JAM-2016
A rectangular area \((A_1)\) is formed by two vectors \(\vec{x}\) and \(\vec{y}\) as shown in figure (i). A new set of vectors, representing the area \((A_2)\) as shown in figure (ii), are given as: \(\vec{u_1}=\vec{x}\) ; \(\vec{u_2}=k\vec{x}+\vec{y}\), where \(k\) is a dimensionless constant.
The Jacobian of the frame \((\vec{u_1},\vec{u_2})\) with respect to \((\vec{x},\vec{y})\) is _________________.
Check Answer
Ans 1
Q.No:4 JAM-2017
Which one of the following graphs represents the derivative \(f'(x)=\frac{df}{dx}\) of the function \(f(x)=\frac{1}{1+x^2}\) most closely (graphs are schematic and not drawn to scale)?
Check Answer
Option A
Q.No:5 JAM-2018
Consider the transformation to a new set of coordinates \(\xi ,\eta\) from rectangular Cartesian coordinates (x, y), where \(\xi=2x+3y\) and \(\eta = 3x-2y\). In the \(\xi ,\eta\) coordinate system, the area element \(dxdy\) is
(A)
\(\frac{1}{13}d \xi d\eta\)
(B)
\(\frac{2}{13}d \xi d\eta\)
(C)
\(5d \xi d\eta\)
(D)
\(\frac{3}{5}d \xi d\eta\)
Check Answer
Option A
Q.No:6 JAM-2018
Let \(f(x)=3x^6-2x^2-8\). Which of the following statements is (are) true?
(A)
The sum of all its roots is zero.
(B)
The product of its roots is \(-\frac{8}{3}\)
(C)
The sum of all its roots is \(\frac{2}{3}\)
(D)
Complex roots are conjugates of each other.
Check Answer
Option A,B,D
Q.No:7 JAM-2018
The coefficient of \(x^3\) in the Taylor expansion of sin(sin x) around \(x=0\) is _________________.
(Specify your answer upto two digits after the decimal point.)
Check Answer
Ans (-0.35)-(-0.30)
Q.No:8 JAM-2020
Which one of the following statements is correct?
Given, \(\begin{pmatrix} n \\ m \end{pmatrix}=\frac{n!}{m!(n-m)!)}\)
(A)
\(cos \hspace{1mm}n\theta=cos^n \theta -\begin{pmatrix} n \\ 2 \end{pmatrix} cos^{n-2}\theta +sin^2 \theta +\begin{pmatrix} n \\ 4 \end{pmatrix}cos^{n-4} \theta + sin^4 \theta - ......\)
(B)
\(sin \hspace{1mm}n\theta=\begin{pmatrix} n \\ 1 \end{pmatrix} cos^{n-1}\theta +sin \theta +\begin{pmatrix} n \\ 3 \end{pmatrix}cos^{n-3} \theta + sin^3 \theta - ......\)
(C)
\(cos \hspace{1mm}n\theta=cos^n \theta +\begin{pmatrix} n \\ 2 \end{pmatrix} cos^{n-2}\theta +sin^2 \theta +\begin{pmatrix} n \\ 4 \end{pmatrix}cos^{n-4} \theta + sin^4 \theta + ......\)
(D)
\(sin \hspace{1mm}n\theta=cos^n \theta -\begin{pmatrix} n \\ 2 \end{pmatrix} cos^{n-2}\theta +sin^2 \theta +\begin{pmatrix} n \\ 4 \end{pmatrix}cos^{n-4} \theta + sin^4 \theta - ......\)
Check Answer
Option A
Q.No:9 JAM-2020
\(\lim_{x \to 0+} x^x\) is equal to
(A)
\(0\)
(B)
\(\infty\)
(C)
\(e\)
(D)
\(1\)
Check Answer
Option D
Q.No:10 JAM-2021
The function \(e^{cos \hspace{0.5mm}x}\) is Taylor expanded about \(x=0\). The coefficient of \(x^2\) is
(A)
\(-\frac{1}{2}\)
(B)
\(-\frac{e}{2}\)
(C)
\(\frac{e}{2}\)
(D)
Zero
Check Answer
Option B
Q.No:11 JAM-2021
Let \((x,y)\) denote the coordinates in a rectangular Cartesian coordinate system \(C\).
Let \((x' , y')\) denote the coordinates in another coordinate system \(C'\), defined by
\[x'=2x+3y\]
\[y'=-3x+4y\]
The area element in \(C'\), is
(A)
\(\frac{1}{17}dx'dy'\)
(B)
\(12dx'dy'\)
(C)
\(dx'dy'\)
(D)
\(x'dx'dy'\)
Check Answer
Option A
Q.No:12 JAM-2022
The integral \(\iint (x^2 + y^2)dxdy\) over the area of a disk of radius 2 in the xy-plane is _______________________ \(\pi\).
Check Answer
Ans 8
Q.No:13 JAM-2023
The plot of the function \(f(x)=||x|-1|\) is
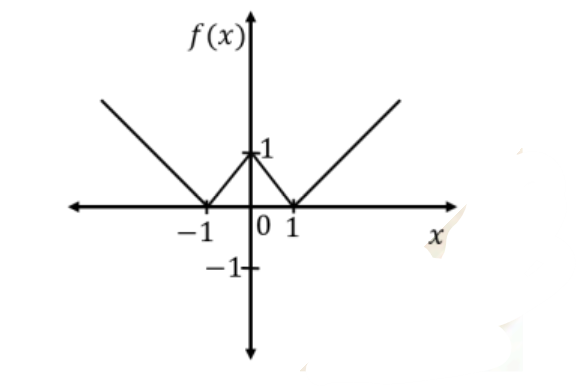
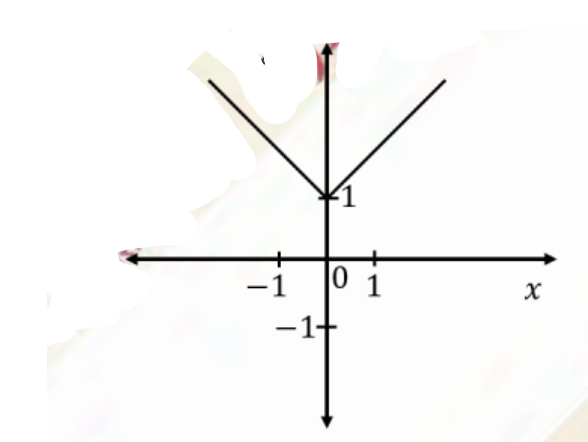
Check Answer
Option B
Q.No:14 JAM-2023
The Jacobian matrix for transforming from (x,y) to another orthogonal coordinates system (u,v) as shown in the figure is
A) \(\frac{1}{\sqrt{2}} \begin{pmatrix} 1&1\\ 1&-1 \end{pmatrix}\)
B) \(\frac{1}{\sqrt{2}} \begin{pmatrix} 1&1\\ -1&1 \end{pmatrix}\)
C) \(\frac{1}{\sqrt{2}} \begin{pmatrix} 1&-1\\ 1&1 \end{pmatrix}\)
D) \(\frac{1}{\sqrt{2}} \begin{pmatrix} 1&-1\\ 1&-1 \end{pmatrix}\)
Check Answer
Option C
Q.No:15 JAM-2023
The absolute error in the value of sin \(\theta\) if approximated up to two terms in the Taylor’s series for \(\theta=60^\circ\) is______________(rounded off to three decimal places).
Check Answer
Ans 0.009-0.011
Q.No:16 JAM-2023
The coordinate system \( (x, y, z) \) is transformed to the system \( (u, v, w) \), as given by:
\[
\begin{aligned}
u &= 2x + 3y - z \\
v &= x - 4y + z \\
w &= x + y
\end{aligned}
\]
The Jacobian of the above transformation is _____.
Check Answer
Ans 4
Q.No:17 JAM-2023
In the Taylor expansion of function, \( F(x) = e^x \sin x \), around \( x = 0 \), the coefficient of \( x^5 \) is____________. (Rounded off to three decimal places)