Q.No:1 GATE-2012
Consider a system in the unperturbed state described by the Hamiltonian, \(H_0=\begin{pmatrix}1&0\\0&1\end{pmatrix}\). The system is subjected to a perturbation of the form \(H'=\begin{pmatrix}\delta&\delta\\\delta&\delta\end{pmatrix}\) where \(\delta\ll 1\). The energy eigenvalues of the perturbed system using the first order perturbation approximation are
(A)
\(1\) and \((1+2\delta)\)
(B)
\((1+\delta)\) and \((1-\delta)\)
(C)
\((1+2\delta)\) and \((1-2\delta)\)
(D)
\((1+\delta)\) and \((1-2\delta)\)
Check Answer
Option A
Q.No:2 GATE-2013
To the given unperturbed Hamiltonian
\[
\begin{bmatrix}
5&2&0\\
2&5&0\\
0&0&2
\end{bmatrix},
\]
we add a small perturbation given by
\[
\varepsilon
\begin{bmatrix}
1&1&1\\
1&1&-1\\
1&-1&1
\end{bmatrix},
\]
where \(\varepsilon\) is a small quantity.
\(\\\)
The ground state eigenvector of the unperturbed Hamiltonian is
(A)
\((1/\sqrt{2}, 1/\sqrt{2}, 0)\)
(B)
\((1/\sqrt{2}, -1/\sqrt{2}, 0)\)
(C)
\((0, 0, 1)\)
(D)
\((1, 0, 0)\)
Check Answer
Option C
Q.No:3 GATE-2013
o the given unperturbed Hamiltonian
\[
\begin{bmatrix}
5&2&0\\
2&5&0\\
0&0&2
\end{bmatrix},
\]
we add a small perturbation given by
\[
\varepsilon
\begin{bmatrix}
1&1&1\\
1&1&-1\\
1&-1&1
\end{bmatrix},
\]
where \(\varepsilon\) is a small quantity.
A pair of eigenvalues of the perturbed Hamiltonian, using first order perturbation theory, is
(A)
\(3+2\varepsilon, 7+2\varepsilon\)
(B)
\(3+2\varepsilon, 2+\varepsilon\)
(C)
\(3, 7+2\varepsilon\)
(D)
\(3, 2+2\varepsilon\)
Check Answer
Option C
Q.No:4 GATE-2014
If \(\vec{L}\) is the orbital angular momentum and \(\vec{S}\) is the spin angular momentum, then \(\vec{L}.\vec{S}\) does NOT commute with
(A)
\(S_z\)
(B)
\(L^2\)
(C)
\(S^2\)
(D)
\((\vec{L}+\vec{S})^2\)
Check Answer
Option A
Q.No:5 GATE-2014
A particle is confined to a one dimensional potential box with the potential
\[
\begin{array}{lll}
V(x) & =0, & 0<x<a \\
& =\infty, & \text{otherwise}
\end{array}
\]
If the particle is subjected to a perturbation, within the box, \(W=\beta x\), where \(\beta\) is a small constant, the first order correction to the ground state energy is
(A)
\(0\)
(B)
\(\alpha \beta/4\)
(C)
\(\alpha \beta/2\)
(D)
\(\alpha \beta\)
Check Answer
Option C
Q.No:6 GATE-2015
A particle is confined in a box of length \(L\) as shown below.

If the potential \(V_0\) is treated as a perturbation, including the first order correction, the ground state energy is
(A)
\(E=\frac{\hbar^2 \pi^2}{2mL^2}+V_0\)
(B)
\(E=\frac{\hbar^2 \pi^2}{2mL^2}-\frac{V_0}{2}\)
(C)
\(E=\frac{\hbar^2 \pi^2}{2mL^2}+\frac{V_0}{4}\)
(D)
\(E=\frac{\hbar^2 \pi^2}{2mL^2}+\frac{V_0}{2}\)
Check Answer
Option D
Q.No:7 GATE-2015
Let the Hamiltonian for two spin-\(1/2\) particles of equal masses \(m\), momenta \(\vec{p}_1\) and \(\vec{p}_2\) and positions \(\vec{r}_1\) and \(\vec{r}_2\) be \(H=\frac{1}{2m}p_1^2+\frac{1}{2m}p_2^2+\frac{1}{2}m\omega^2(r_1^2+r_2^2)+k\vec{\sigma}_1\cdot \vec{\sigma}_2\), where \(\vec{\sigma}_1\) and \(\vec{\sigma}_2\) denote the corresponding Pauli matrices, \(\hbar \omega=0.1 eV\) and \(k=0.2 eV\). If the ground state has net spin zero, then the energy (in eV) is __________.
Check Answer
Ans (-0.3)
Q.No:8 GATE-2016
A hydrogen atom is in its ground state. In the presence of a uniform electric field \(\vec{E}=E_0 \hat{z}\), the leading order change in its energy is proportional to \((E_0)^n\). The value of the exponent \(n\) is _____________.
Check Answer
Ans 2
Q.No:9 GATE-2016
If \(\vec{s}_1\) and \(\vec{s}_2\) are the spin operators of the two electrons of a \ce{He} atom, the value of \(\langle \vec{s}_1, \vec{s}_2\rangle\) for the ground state is
(A)
\(-\frac{3}{2}\hbar^2\)
(B)
\(-\frac{3}{4}\hbar^2\)
(C)
\(0\)
(D)
\(\frac{1}{4}\hbar^2\)
Check Answer
Option B
Q.No:10 GATE-2017
A one dimensional simple harmonic oscillator with Hamiltonian \(H_0=\frac{p^2}{2m}+\frac{1}{2}kx^2\) is subjected to a small perturbation, \(H_1=\alpha x+\beta x^3+\gamma x^4\). The first order correction to the ground state energy is dependent on
(A)
only \(\beta\)
(B)
\(\alpha\) and \(\gamma\)
(C)
\(\alpha\) and \(\beta\)
(D)
only \(\gamma\)
Check Answer
Option D
Q.No:11 GATE-2018
The intrinsic/permanent electric dipole moment in the ground state of hydrogen atom is (\(a_0\) is the Bohr radius)
(A)
\(-3ea_0\)
(B)
zero
(C)
\(ea_0\)
(D)
\(3ea_0\)
Check Answer
Option B
Q.No:12 GATE-2018
The ground state energy of a particle of mass \(m\) in an infinite potential well is \(E_0\). It changes to \(E_0(1+\alpha \times 10^{-3})\), when there is a small potential bump of height \(V_0=\frac{\pi^2 \hbar^2}{50mL^2}\) and width \(a=L/100\), as shown in the figure. The value of \(\alpha\) is ___________ (up to two decimal places).

Check Answer
Ans 0.78-0.82
Q.No:13 GATE-2019
An electric field \(\vec{E}=E_0 \hat{z}\) is applied to a Hydrogen atom in \(n=2\) excited state. Ignoring spin, the \(n=2\) state is fourfold degenerate, which in the \(|l, m\rangle\) basis are given by \(|0, 0\rangle, |1, 1\rangle, |1, 0\rangle\) and \(|1, -1\rangle\). If \(H'\) is the interaction Hamiltonian corresponding to the applied electric field, which of the following matrix elements is nonzero?
(A) \(\langle 0, 0|H'|0, 0\rangle\)
(B)
\(\langle 0, 0|H'|1, 1\rangle\)
(C)
\(\langle 0, 0|H'|1, 0\rangle\)
(D)
\(\langle 0, 0|H'|1, -1\rangle\)
Check Answer
Option C
Q.No:14 GATE-2019
The spin-orbit interaction term of an electron moving in a central field is written as \(f(r)\vec{l}\cdot \vec{s}\), where \(r\) is the radial distance of the electron from the origin. If an electron moves inside a uniformly charged sphere, then
(A)
\(f(r)=\text{constant}\)
(B)
\(f(r)\propto r^{-1}\)
(C)
\(f(r)\propto r^{-2}\)
(D)
\(f(r)\propto r^{-3}\)
Check Answer
Option A
Q.No:15 GATE-2019
The Hamiltonian of a system is \(H=\begin{pmatrix}1&\varepsilon\\\varepsilon&-1\end{pmatrix}\) with \(\varepsilon\ll 1\). The fourth order contribution to the ground state energy of \(H\) is \(\gamma \varepsilon^4\). The value of \(\gamma\) (rounded off to three decimal places) is ________.
Check Answer
Ans 0.125
Q.No:16 GATE-2020
Consider the Hamiltonian \(\hat{H}=\hat{H}_0+\hat{H}'\) where \(\hat{H}_0=\begin{pmatrix}E&0&0\\0&E&0\\0&0&E\end{pmatrix}\) and \(\hat{H}'\) is the time independent perturbation given by \(\hat{H}'=\begin{pmatrix}0&k&0\\k&0&k\\0&k&0\end{pmatrix}\), where \(k>0\). If, the maximum energy eigenvalue of \(\hat{H}\) is \(3 eV\) corresponding to \(E=2 eV\), the value of \(k\) (rounded off to three decimal places) in eV is _________.
Check Answer
Ans 0.706-0.708
Q.No:17 GATE-2021
Consider a particle in a one-dimensional infinite potential well with its walls at \(x=0\) and \(x=L\). The system is perturbed as shown in the figure.

The first order correction to the energy eigenvalue is
(A)
\(\frac{V_0}{4}\)
(B)
\(\frac{V_0}{3}\)
(C)
\(\frac{V_0}{2}\)
(D)
\(\frac{V_0}{5}\)
Check Answer
Option C
Q.No:18 GATE-2021
For a two-nucleon system in spin singlet state, the spin is represented through the Pauli matrices \(\sigma_1, \sigma_2\) for particles 1 and 2, respectively. The value of \((\sigma_1\cdot\sigma_2)\) (in integer) is _______________.
Check Answer
Ans (-3)
Q.No:19 GATE-2021
The spin \(\vec{S}\) and orbital angular momentum \(\vec{L}\) of an atom precess about \(\vec{J}\), the total angular momentum. \(\vec{J}\) precesses about an axis fixed by a magnetic field \(\vec{B}_1=2B_0 \hat{z}\), where \(B_0\) is a constant. Now the magnetic field is changed to \(\vec{B}_2=B_0(\hat{x}+\sqrt{2}\hat{y}+\hat{z})\). Given the orbital angular momentum quantum number \(l=2\) and spin quantum number \(s=1/2\), \(\theta\) is the angle between \(\vec{B}_1\) and \(\vec{J}\) for the largest possible values of total angular quantum number \(j\) and its \(z\)-component \(j_z\). The value of \(\theta\) (in degree, rounded off to the nearest integer) is ______________.
Check Answer
Ans 27-93
Q.No:20 GATE-2022
Consider a particle in three different boxes of width \(L\). The potential inside the boxes vary as shown in figures (i), (ii) and (iii) with \(V_0\ll \frac{\hbar^2 \pi^2}{2mL^2}\). The corresponding ground-state energies of the particle are \(E_1, E_2\) and \(E_3\), respectively. Then

(a)
\(E_2>E_1>E_3\)
(b)
\(E_3>E_1>E_2\)
(c)
\(E_2>E_3>E_1\)
(d)
\(E_3>E_2>E_1\)
Check Answer
Option a
Q.No:21 GATE-2022
A particle of mass \(m\) in the \(x\)-\(y\) plane is confined in an infinite two-dimensional well with vertices at \((0, 0), (0, L), (L, L), (L, 0)\). The eigenfunctions of this particle are \(\psi_{n_x, n_y}=\frac{2}{L}\sin{\left(\frac{n_x \pi x}{L}\right)}\sin{\left(\frac{n_y \pi y}{L}\right)}\). If perturbation of the form \(V=Cxy\), where \(C\) is a real constant, is applied, then which of the following statements are correct for the first excited state?
(a)
The unperturbed energy is \(\frac{3\pi^2 \hbar^2}{2mL^2}\)
(b)
The unperturbed energy is \(\frac{5\pi^2 \hbar^2}{2mL^2}\)
(c)
First order energy shift due to the applied perturbation is zero
(d)
The shift (\(\delta\)) in energy due to the applied perturbation is determined by an equation of the form \(\left|\begin{matrix}a-\delta&b\\b&a-\delta\end{matrix}\right|=0\), where \(a\) and \(b\) are real, non-zero constants
Check Answer
Option b,d
Q.No:22 GATE-2024
The non-relativistic Hamiltonian for a single electron atom is
\[ H_0 = \frac{p^2}{2m} - V(r) \]
where \(V(r)\) is the Coulomb potential and \(m\) is the mass of the electron. Considering the spin-orbit interaction term
\[ H' = \frac{1}{2m^2c^2} \frac{1}{r} \frac{dV}{dr} \vec{L} \cdot \vec{S} \]
added to \(H_0\), which of the following statement is/are true?
1) \(H'\) commutes with \(L^2\)
2) \(H'\) commutes with \(L_z\) and \(S_z\)
3) For a given value of principal quantum number \(n\) and orbital angular momentum quantum number \(l\), there are \(2(2l + 1)\) degenerate eigenstates of \(H_0\)
4) \(H_0\), \(L^2\), \(S^2\), \(L_z\), and \(S_z\) have a set of simultaneous eigenstates
Check Answer
Option 1,3,4
Q.No:23 GATE-2024
A particle of mass \( m \) in an infinite potential well of width \( a \) is subjected to a perturbation, \( V' = \frac{h^2}{40ma^2} \) as shown in figure,

where \( h \) is Planck's constant.
The first order energy shift of the fourth energy eigenstate due to this perturbation is
\[
\frac{h^2}{Nma^2}
\]
The value of \( N \) is__________ (in integer).
Check Answer
Ans 160
Q.No:24 GATE-2025
A two–level quantum system has energy eigenvalues \(E_{1}\) and \(E_{2}\).
A perturbing potential \(H' = \lambda \Delta \sigma_{x}\) is introduced, where \(\Delta\) is a constant having dimensions of energy, \(\lambda\) is a small dimensionless parameter, and
\[
\sigma_{x} =
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}
\]
The magnitudes of the first and the second order corrections to \(E_{1}\) due to \(H'\), respectively, are
(1) \(0 \text{ and } \frac{\lambda^{2} \Delta^{2}}{|E_{1} - E_{2}|}\)
(2) \(\frac{|\lambda \Delta|}{2} \text{ and } \frac{\lambda^{2} \Delta^{2}}{|E_{1} - E_{2}|}\)
(3) \(|\lambda \Delta| \text{ and } \frac{\lambda^{2} \Delta^{2}}{|E_{1} - E_{2}|}\)
(4) \(0 \text{ and } \frac{1}{2}\,\frac{\lambda^{2} \Delta^{2}}{|E_{1} - E_{2}|}\)
Check Answer
Option 1
Q.No: 1 CSIR Dec-2014
The Hamiltonian \(H_0\) for a three-state quantum system is given by the matrix \(H_0=\begin{pmatrix}1&0&0\\0&2&0\\0&0&2\end{pmatrix}\). When perturbed by \(H'=\epsilon\begin{pmatrix}0&1&0\\1&0&1\\0&1&0\end{pmatrix}\) where \(\epsilon\ll 1\), the resulting shift in the energy eigenvalue \(E_0=2\) is
(1)
\(\epsilon, -2\epsilon\)
(2)
\(-\epsilon, 2\epsilon\)
(3)
\(\pm \epsilon\)
(4)
\(\pm 2\epsilon\)
Check Answer
Option 3
Q.No:2 CSIR Dec-2014
The effective spin-spin interaction between the electron spin \(\vec{s}_e\) and the proton spin \(\vec{s}_p\) in the ground state of the Hydrogen atom is given by \(H'=a\vec{s}_e\cdot \vec{s}_p\). As a result of this interaction, the energy levels split by an amount
(1)
\(\frac{1}{2}a\hbar^2\)
(2)
\(2a\hbar^2\)
(3)
\(a\hbar^2\)
(4)
\(\frac{3}{2}a\hbar^2\)
Check Answer
Option 3
Q.No:3 CSIR Dec-2015
A hydrogen atom is subjected to the perturbation \(V_{pert}(\mathbf{r})=\epsilon \cos{(2r/a_0)}\), where \(a_0\) is the Bohr radius. The change in the ground state energy to first order in \(\epsilon\) is
(1)
\(\epsilon/4\)
(2)
\(\epsilon/2\)
(3)
\(-\epsilon/2\)
(4)
\(-\epsilon/4\)
Check Answer
Option 4
Q.No:4 CSIR June-2016
Consider a particle of mass \(m\) in a potential \(V(x)=\frac{1}{2}m\omega^2 x^2+g\cos{kx}\). The change in the ground state energy, compared to the simple harmonic potential \(\frac{1}{2}m\omega^2 x^2\), to first order in \(g\) is
(1)
\(g\exp{\left(-\frac{k^2 \hbar}{2m\omega}\right)}\)
(2)
\(g\exp{\left(\frac{k^2 \hbar}{2m\omega}\right)}\)
(3)
\(g\exp{\left(-\frac{2k^2 \hbar}{m\omega}\right)}\)
(4)
\(g\exp{\left(-\frac{k^2 \hbar}{4m\omega}\right)}\)
Check Answer
Option 4
Q.No: 5 CSIR June-2017
The Coulomb potential \(V(r)=-e^2/r\) of a hydrogen atom is perturbed by adding \(H'=bx^2\) (where \(b\) is a constant) to the Hamiltonian. The first order correction to the ground state energy is (The ground state wavefunction is \(\psi_0=\frac{1}{\sqrt{\pi a_0^2}} e^{-r/a_0}\).)
(1)
\(2ba_0^2\)
(2)
\(ba_0^2\)
(3)
\(ba_0^2/2\)
(4)
\(\sqrt{2}ba_0^2\)
Check Answer
Option 2
Q.No: 6 CSIR Dec-2017
Consider a one-dimensional infinite square well
\[
V(x)=
\left\{
\begin{array}{ll}
0 & \text{for }0<x <a,\\
\infty & \text{otherwise}
\end{array}
\right.
\]
If a perturbation
\[
\Delta V(x)=
\left\{
\begin{array}{ll}
V_0 & \text{for }0<x <a/3,\\
0 & \text{otherwise}
\end{array}
\right.
\]
is applied, then the correction to the energy of the first excited state, to first order in \(\Delta V\), is nearest to
(1)
\(V_0\)
(2)
\(0.16 V_0\)
(3)
\(0.2 V_0\)
(4)
\(0.33 V_0\)
Check Answer
Option
Q.No: 7 CSIR June-2018
A particle of mass \(m\) is constrained to move in a circular ring of radius \(R\). When a perturbation \(V'=\frac{a}{R^2}\cos^2{\phi}\) (where \(a\) is a real constant) is added, the shift in energy of the ground state, to first order in \(a\), is
(1)
\(a/R^2\)
(2)
\(2a/R^2\)
(3)
\(a/(2R^2)\)
(4)
\(a/(\pi R^2)\)
Check Answer
Option 3
Q.No: 8 CSIR June-2019
The infinite square-well potential of a particle in a box of size \(a\) is modified as shown in the figure below (assume \(\Delta \ll a\))
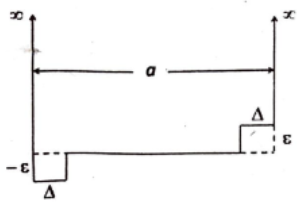
The energy of the ground state, compared to the ground state energy before the perturbation was added
(1)
increases by a term of order \(\varepsilon\)
(2)
decreases by a term of order \(\varepsilon\)
(3)
increases by a term of order \(\varepsilon^2\)
(4)
decreases by a term of order \(\varepsilon^2\)
Check Answer
Option 4
Q.No: 9 CSIR Dec-2019
The Hamiltonian of two interacting particles, one with spin \(1\) and the other with spin \(\frac{1}{2}\), is given by \(H=A\mathbf{S}_1\cdot \mathbf{S}_2+B(S_{1x}+S_{2x})\), where \(\mathbf{S}_1\) and \(\mathbf{S}_2\) denote the spin operators of the first and second particles, respectively, and \(A\) and \(B\) are positive constants. The largest eigenvalue of this Hamiltonian is
(1)
\(\frac{1}{2}(A\hbar^2+3B\hbar)\)
(2)
\(3A\hbar^2+B\hbar\)
(3)
\(\frac{1}{2}(3A\hbar^2+B\hbar)\)
(4)
\(A\hbar^2+3B\hbar\)
Check Answer
Option 1
Q.No: 10 Assam CSIR Dec-2019
Consider the degenerate first excited states \(n=2, l=1\) of the hydrogen atom. If its Hamiltonian is modified by adding \(H_1=\frac{\alpha}{\hbar} L_x\), where \(L_x\) is the \(x\)-component of the orbital angular momentum, the changes in the energies of the states labelled by \(m=0, +1\) and \(-1\) are, respectively,
(1)
\(0, \alpha\) and \(-\alpha\)
(2)
\(\alpha, 2\alpha\) and \(0\)
(3)
\(\alpha, 0\) and \(-\alpha\)
(4)
\(0, 2\alpha\) and \(-2\alpha\)
Check Answer
Option 1
Q.No: 11 Assam CSIR Dec-2019
A quantum particle in a one-dimensional box of length \(L\) is perturbed by a barrier of height \(\epsilon\) and length \(a\), as shown in the figure.

Assume that \(\epsilon\) is much smaller than the ground state energy of the particle in the unperturbed box and \(a\ll L\). The changes of the two lowest energy eigenvalues, to first order in \(\epsilon\) and first order in \(a\), are, respectively,
(1)
\(\frac{2\epsilon a}{L}\) and \(-\frac{2\epsilon a}{L}\)
(2)
\(0\) and \(\frac{2\epsilon a}{L}\)
(3)
\(-\frac{2\epsilon a}{L}\) and \(0\)
(4)
\(\frac{2\epsilon a}{L}\) and \(0\)
Check Answer
Option 4
Q.No: 12 CSIR June-2020
Two coupled oscillators in a potential \(V(x, y)=\frac{1}{2}kx^2+2xy+\frac{1}{2}ky^2\) (\(k>2\)) can be decoupled into two independent harmonic oscillators (coordinates: \(x', y'\)) by means of an appropriate transformation \(\begin{pmatrix}x'\\y'\end{pmatrix}=S\begin{pmatrix}x\\y\end{pmatrix}\). The transformation matrix \(S\) is
(a)
\(\begin{pmatrix}\frac{1}{\sqrt{2}}&1\\1&-\frac{1}{\sqrt{2}}\end{pmatrix}\)
(b)
\(\begin{pmatrix}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{pmatrix}\)
(c)
\(\begin{pmatrix}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{pmatrix}\)
(d)
\(\begin{pmatrix} 0 &-1 \\\ 1 & 0 \end{pmatrix}\)
Check Answer
Option b
Q.No: 13 CSIR June-2020
If we take the nuclear spin \(I\) into account, the total angular momentum is \(\vec{F}=\vec{L}+\vec{S}+\vec{I}\), where \(\vec{L}\) and \(\vec{S}\) are the orbital and spin angular momenta of the electron. The Hamiltonian of the hydrogen atom is corrected by the additional interaction \(\lambda \vec{I}\cdot (\vec{L}+\vec{S})\), where \(\lambda>0\) is a constant. The total angular momentum quantum number \(F\) of the \(p\)-orbital state with the lowest energy is
(a)
\(0\)
(b)
\(1\)
(c)
\(1/2\)
(d)
\(3/2\)
Check Answer
Option b
Q.No: 14 CSIR Sep-2022
To first order in perturbation theory, the energy of the ground state of the Hamiltonian
\[
H=\frac{p^2}{2m} + \frac{1}{2} m \omega^2 x^2
+ \frac{\hbar \omega}{\sqrt{512}}exp\left[-\frac{m\omega}{\hbar}x^2\right]
\]
(1)
\(\frac{15}{32}\hbar \omega\)
(2)
\(\frac{17}{32}\hbar \omega\)
(3)
\(\frac{19}{32}\hbar \omega\)
(4)
\(\frac{21}{32}\hbar \omega\)
Check Answer
Option 2
Q.No: 15 CSIR June 2023
A particle in one dimension is in an infinite potential well between \(\frac{-L}{2}\le x\le \frac{L}{2}\). For a perturbation \(\epsilon \cos(\frac{\pi x}{L})\), where \(\epsilon\) is a small constant, the change in the energy of the ground state, to first order in \(\epsilon\), is
1) \(\frac{5\epsilon}{\pi}\)
2) \(\frac{10\epsilon}{3\pi}\)
3) \(\frac{8\epsilon}{3\pi}\)
4) \(\frac{4\epsilon}{\pi}\)
Check Answer
Option 3
Q.No: 16 CSIR June 2024
An integral is given by
\[
\int_{-\infty}^{\infty} dx \int_{-\infty}^{\infty} dy \exp\left[-(x^2+y^2+2axy)\right],
\]
where \(a\) is a real parameter. The full range of values of \(a\) for which the integral is finite, is:
1) \(-\infty < a < \infty\)
2) \(-2 < a < 2\)
3) \(-1 < a < 1\)
4) \(-1 \leq a \leq 1\)
Check Answer
Option 3
Q.No: 17 CSIR Dec 2024
Consider a particle in a one–dimensional infinite potential well between \(0 \le x \le L\).
If a small perturbation,
\[
V(x) = \lambda \cos\!\left(\frac{\pi x}{L}\right),
\]
(where \(\lambda \ll 1\)) is applied, the first–order energy correction to the ground state is
1) \(\lambda\)
2) 0
3)\(-\lambda\)
4) \(2\lambda\)
Check Answer
Option 2
Q.No: 18 CSIR June 2025
The ground state wavefunction for the hydrogen atom is
\[
\psi_{0} = \sqrt{\frac{1}{\pi a_{0}^{3}}}\, e^{-r/a_{0}}
\]
where \(a_{0}\) is the Bohr radius. Considering an additional potential \(H'\) as a perturbation to the hydrogen atom Hamiltonian, given by
\[
H' = \left(\frac{e^{2}}{4\pi\epsilon_{0}}\right)
\left[\frac{1}{r} - \frac{1}{R}\right]; 0 < r < R,
\]
\(H'=0;\) otherwise.
where \(R\) is the radius of the proton, \(R \ll a_{0}\). The shift in the ground state energy due to \(H'\) is
1) \(\left(\frac{e^{2}}{4\pi\epsilon_{0} a_{0}}\right)\frac{4R^{2}}{3a_{0}^{2}}\)
2) \(\left(\frac{e^{2}}{4\pi\epsilon_{0} a_{0}}\right)\frac{R}{a_{0}}\)
3) \(-\left(\frac{e^{2}}{4\pi\epsilon_{0} a_{0}}\right)\frac{2R^{2}}{a_{0}^{2}}\)
4) \(\left(\frac{e^{2}}{4\pi\epsilon_{0} a_{0}}\right)\frac{2R^{2}}{3a_{0}^{2}}\)
