Q.No:1 CSIR Dec-2014
Two independent random variables \(m\) and \(n\), which can take the integer values \(0, 1, 2, \cdots, \infty\), follow the Poisson distribution, with distinct mean values \(\mu\) and \(\nu\) respectively. Then
(1)
the probability distribution of the random variable \(l=m+n\) is a binomial distribution.
(2)
the probability distribution of the random variable \(r=m-n\) is also a Poisson distribution.
(3)
the variance of the random variable \(l=m+n\) is equal to \(\mu+\nu\).
(4)
the mean value of the random variable \(r=m-n\) is equal to \(0\).
Check Answer
Option 3
Q.No:2 CSIR Dec-2014
A random walker takes a step of unit length in the positive direction with probability \(2/3\) and a step of unit length in the negative direction with probability \(1/3\). The mean displacement of the walker after \(n\) steps is
(1)
\(n/3\)
(2)
\(n/8\)
(3)
\(2n/3\)
(4)
\(0\)
Check Answer
Option 1
Q.No:3 CSIR June-2015
Three real variables a, b and c are each randomly chosen from a uniform probability distribution in the interval \([0, 1]\). The probability that \(a + b > 2c\) is
(1)
\(\frac{3}{4}\)
(2)
\(\frac{2}{3}\)
(3)
\(\frac{1}{2}\)
(4)
\(\frac{1}{4}\)
Check Answer
Option 3
Q.No:4 CSIR Dec-2015
Consider a random walker on a square lattice. At each step the walker moves to a nearest neighbour site with equal probability for each of the four sites. The walker starts at the origin and takes \(3\) steps. The probability that during this walk no site is visited more than once is
(1)
\(12/27\)
(2)
\(27/64\)
(3)
\(3/8\)
(4)
\(9/16\)
Check Answer
Option 4
Q.No:5 CSIR Dec-2016
Consider a continuous time random walk. If a step has taken place at time \(t=0\), the probability that the next step takes place between \(t\) and \(t+dt\) is given by \(bt dt\), where \(b\) is a constant. What is the average time between successive steps?
(1)
\(\sqrt{\frac{2\pi}{b}}\)
(2)
\(\sqrt{\frac{\pi}{b}}\)
(3)
\(\frac{1}{2}\sqrt{\frac{\pi}{b}}\)
(4)
\(\sqrt{\frac{\pi}{2b}}\)
Check Answer
Option 4
Q.No:6 CSIR Dec-2016
Consider a random walk on an infinite two-dimensional triangular lattice, a part of which is shown in the figure below.

If the probabilities of moving to any of the nearest neighbour sites are equal, what is the probability that the walker returns to the starting position at the end of exactly three steps?
(1)
\(\frac{1}{36}\)
(2)
\(\frac{1}{216}\)
(3)
\(\frac{1}{18}\)
(4)
\(\frac{1}{12}\)
Check Answer
Option 3
Q.No:7 CSIR June-2017
The random variable \(x\) (\(-\infty< x< \infty\)) is distributed according to the normal distribution \(P(x)=\frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{x^2}{2\sigma^2}}\). The probability density of the random variable \(y=x^2\) is
(1)
\(\frac{1}{\sqrt{2\pi \sigma^2 y}} e^{-y/2\sigma^2}, 0\leq y< \infty\)
(2)
\(\frac{1}{2\sqrt{2\pi \sigma^2 y}} e^{-y/2\sigma^2}, 0\leq y< \infty\)
(3)
\(\frac{1}{\sqrt{2\sigma^2}} e^{-y/2\sigma^2}, 0\leq y< \infty\)
(4)
\(\frac{1}{\sqrt{2\pi \sigma^2 y}} e^{-y/\sigma^2}, 0\leq y< \infty\)
Check Answer
Option 1
Q.No:8 CSIR June-2017
A random variable \(n\) obeys Poisson statistics. The probability of finding \(n=0\) is \(10^{-6}\). The expectation value of \(n\) is nearest to
(1)
\(14\)
(2)
\(10^6\)
(3)
\(e\)
(4)
\(10^2\)
Check Answer
Option 1
Q.No:9 CSIR Dec-2018
A particle hops on a one-dimensional lattice with lattice spacing \(a\). The probability of the particle to hop to the neighbouring site to its right is \(p\), while the corresponding probability to hop to the left is \(q=1-p\). The root-mean-squared deviation \(\Delta x=\sqrt{\langle x^2\rangle-\langle x\rangle^2}\) in displacement after \(N\) steps, is

(1)
\(a\sqrt{Npq}\)
(2)
\(aN\sqrt{pq}\)
(3)
\(2a\sqrt{Npq}\)
(4)
\(a\sqrt{N}\)
Check Answer
Option 3
Q.No:10 CSIR June-2019
At each time step, a random walker in one-dimension either remains at the same point with probability \(\frac{1}{4}\), or moves by a distance \(\Delta\) to the right or left with probabilities \(3/8\) each. After \(N\) time steps, its root mean squared displacement is
(1)
\(\Delta \sqrt{N}\)
(2)
\(\Delta \sqrt{\frac{9N}{16}}\)
(3)
\(\Delta \sqrt{\frac{3N}{4}}\)
(4)
\(\Delta \sqrt{\frac{3N}{8}}\)
Check Answer
Option 3
Q.No:11 CSIR Dec-2019
A box contains \(5\) white and \(4\) black balls. Two balls are picked together at random from the box. What is the probability that these two balls are of different colours?
(1)
\(1/2\)
(2)
\(5/18\)
(3)
\(1/3\)
(4)
\(5/9\)
Check Answer
Option 4
Q.No:12 CSIR Dec-2019
A particle hops randomly from a site to its nearest neighbour in each step on a square lattice of unit lattice constant. The probability of hopping to the positive \(x\)-direction is \(0.3\), to the negative \(x\)-direction is \(0.2\), to the positive \(y\)-direction is \(0.2\) and to the negative \(y\)-direction is \(0.3\). If a particle starts from the origin, its mean positive after \(N\) steps is
(1)
\(\frac{1}{10}N(-\hat{i}+\hat{j})\)
(2)
\(\frac{1}{10}N(\hat{i}-\hat{j})\)
(3)
\(N(0.3\hat{i}-0.2\hat{j})\)
(4)
\(N(0.2\hat{i}-0.3\hat{j})\)
Check Answer
Option 2
Q.No:13 Assam CSIR Dec-2019
There are \(n\) distinguishable balls which are to be put in \(n\) boxes, where each box can contain at most \((n-1)\) balls. The number of ways in which the balls can be distributed in the boxes is
(1)
\(n(n^{n-1}-1)\)
(2)
\((n-1)^n\)
(3)
\(n^{n-1}\)
(4)
\(n!-n\)
Check Answer
Option 1
Q.No:14 Assam CSIR Dec-2019
A particle hops randomly from one site to a neighbouring site on a one-dimensional lattice. The probability of hopping to the left is \(p\) and that to the right is \(q\). After exactly \(4\) hops the probability of finding the particle at the starting site is
(1)
\(p^2 q^2\)
(2)
\(2p^2 q^2\)
(3)
\(4p^2 q^2\)
(4)
\(6p^2 q^2\)
Check Answer
Option 4
Q.No:15 Assam CSIR Dec-2019
The photon flux in an argon laser is \(2.5\times 10^5 m^{-2}s^{-1}\). A photo detector is used to convert photons to electrons with a \(10\%\) conversion efficiency. Assuming Poisson statistics, the mean value of and the fluctuations in the number of photons that are detected per unit area in a time interval of \(0.1 s\) are, respectively, nearest to
(1)
\(2500\) and \(50\)
(2)
\(2500\) and \(250\)
(3)
\(250\) and \(12\)
(4)
\(25000\) and \(158\)
Check Answer
Option 1
Q.No:16 CSIR June-2020
A basket consists of an infinite number of red and black balls in the proportion \(p:(1-p)\). Three balls are drawn at random without replacement. The probability of their being two red and one black is a maximum for
(a)
\(p=\frac{3}{4}\)
(b)
\(p=\frac{3}{5}\)
(c)
\(p=\frac{1}{2}\)
(d)
\(p=\frac{2}{3}\)
Check Answer
Option d
Q.No:17 CSIR Feb-2022
The position of a particle in one dimension changes in discrete steps. With each step it
moves to the right, however, the length of the step is drawn from a uniform distribution from the
interval
\([\lambda-\frac{1}{2}\omega , \lambda+\frac{1}{2}\omega]\) , where \(\lambda\) and \(\omega\) are positive constants. If \(X\) denotes the distance
from the starting point after \(N\) steps, the standard deviation \(\sqrt{[x^2]-[x]^2} \) for large values of
\(N\) is
(1)
\(\frac{\lambda}{2}\times \sqrt{N}\)
(2)
\(\frac{\lambda}{2}\times \sqrt{\frac{N}{3}}\)
(3)
\(\frac{\omega}{2}\times \sqrt{N}\)
(4)
\(\frac{\omega}{2}\times \sqrt{\frac{N}{3}}\)
Check Answer
Option 4
Q.No:18 CSIR Feb-2022
A discrete random variable X takes a value from the set \(\{-1,.,1,2\}\) with the
corresponding probabilities \(p(X)=3/10,2/10,2/10\) and \(3/10\), respectively. The probability
distribution \(q(Y)=(q(0),q(1),q(4))\) of the random variable \(Y=X^2\) is
(1)
\((\frac{1}{5},\frac{3}{5},\frac{1}{5})\)
(2)
\((\frac{1}{5},\frac{1}{2},\frac{3}{10})\)
(3)
\((\frac{2}{5},\frac{2}{5},\frac{1}{5})\)
(4)
\((\frac{3}{10},\frac{3}{10},\frac{2}{5})\)
Check Answer
Option 2
Q.No:19 CSIR Sep-2022
A walker takes steps, each of length \(L\), , randomly in the directions along east, west, north and south. After four steps
its distance from the starting point is \(d\). The probability that \(d\leq 3L\) is
(1)
\(63/64\)
(2)
\(59/64\)
(3)
\(57/64\)
(4)
\(55/64\)
Check Answer
Option 4
Q.No:20 CSIR Sep-2022
A bucket contains 6 red and 4 blue balls. A ball is taken out of the bucket at random and two balls of the same colour are put back. This step is repeated once more. The probability that the numbers of red and blue balls are equal at the end, is
(1)
4/11
(2)
2/11
(3)
1/4
(4)
3/4
Check Answer
Option 2
Q.No:21 CSIR-June-2023
A random variable \(Y\) obeys a normal distribution
\(P(Y)=\frac{1}{\sigma \sqrt{2\pi}}exp[-\frac{(Y-\mu)^2}{2\sigma^2}]\)
The mean value of \(e^Y\) is
1) \(e^{\mu+\frac{\sigma^2}{2}}\)
2) \(e^{\mu-\sigma^2}\)
3) \(e^{\mu+\sigma^2}\)
4) \(e^{\mu-\frac{\sigma^2}{2}}\)
Check Answer
Option 1
Q.No:22 CSIR-Dec-2023
A photon inside the sun executes a random walk process. Given the radius of the sun \( \approx 7 \times 10^8 \) km and mean free path of a photon \( \approx 10^{-3} \) m, the time taken by the photon to travel from the centre to the surface of the sun is closest to
1) \( 10^6 \) sec
2) \( 10^{24} \) sec
3) \( 10^{12} \) sec
4) \( 10^{18} \) sec
Check Answer
Option 3
Q.No:23 CSIR-June-2023
A jar \(J1\) contains equal number of balls of red, blue and green colours, while another jar \(J2\) contains balls of only red and blue colours, which are also equal in number. The probability of choosing \(J1\) is twice as large as choosing \(J2\). If a ball picked at random from one of the jars turns out to be red, the probability that it came from \(J1\) is
1) \(\frac{2}{3}\)
2) \(\frac{3}{5}\)
3) \(\frac{2}{5}\)
4) \(\frac{4}{7}\)
Check Answer
Option 4
Q.No:24 CSIR-June-2023
Two random walkers A and B walk on a one-dimensional lattice. The length of each step taken by A is one, while the same for B is two, however, both move towards right or left with equal probability. If they start at the same point, the probability that they meet after 4 steps, is
1) \(\frac{9}{64}\)
2) \(\frac{5}{32}\)
3) \(\frac{11}{64}\)
4) \(\frac{3}{16}\)
Check Answer
Option 3
Q.No:25 CSIR-June-2023
An astronomer observes 500 objects and classifies them as either of type \( A \) or type \( B \).
She finds 148 objects to be of type \( B \). Assuming a binomial distribution, the best estimate of the fraction of type \( A \) objects and its associated standard deviation respectively are:
1) \( 0.704, \, 0.002 \)
2) \( 0.70, \, 0.02 \)
3) \( 0.704, \, 0.031 \)
4) \( 0.72, \, 0.03 \)
Check Answer
Option 2
Q.No:26 CSIR-June-2023
A random walker takes a step of unit length towards right or left at any discrete time step. Starting from \( x = 0 \) at time \( t = 0 \), it goes right to reach \( x = 1 \) at \( t = 1 \). Hereafter if it repeats the direction taken in the previous step with probability \( p \), the probability that it is again at \( x = 1 \) at \( t = 3 \) is:
1) \( 1-p \)
2) \( (1-p)^2 \)
3) \( 2p(1-p) \)
4) \( 4p^2(1-p) \)
Check Answer
Option 1
Q.No:27 CSIR-June-2025
A class has 60% boys and 40% girls. In an examination 8% of the boys and 12% of the girls got an ‘A’ grade. If a randomly selected student had an ‘A’ grade, what is the probability that the student is male?
1) 0.7
2) 0.6
3) 0.4
4) 0.5
Check Answer
Option 4
Q.No:28 CSIR-June-2025
From a straight-line segment of unit length, three points are chosen at random, one after another. The probability that they are in increasing order is
1) \(\frac{1}{3}\)
2) \(\frac{1}{8}\)
3) \(\frac{1}{9}\)
4)\(\frac{1}{6}\)
Check Answer
Option 4
Q.No:29 CSIR-June-2025
Two discrete time random walkers start from the point \(x = 0\) at time \(t = 0\) taking discrete steps of unit length along the x axis. The first walker is unbiased and the second walker is biased to move towards the right with probability \(p\). The probability that they are at a distance of 2 units from each other at both time steps \(t = 1\) and \(t = 2\) is
1) \(\frac{1}{4}\)
2) \(\frac{1}{2} - \frac{p}{2}\)
3) \(1 - \frac{3p}{4}\)
4) \(\frac{p}{2}\)
Check Answer
Option 1
Q.No:1 JEST-2012
An unbiased die is cast twice. The probability that the positive difference (\(\text{bigger}−\text{smaller}\)) between the two numbers is \(2\) is
(a)
\(1/9\)
(b)
\(2/9\)
(c)
\(1/6\)
(d)
\(1/3\)
Check Answer
Option b
Q.No:2 JEST-2013
Two drunks start out together at the origin, each having equal probability of making a step simultaneously to the left or right along the \(x\) axis. The probability that they meet after \(n\) steps is
(a)
\(\frac{1}{4^n}\frac{2n!}{n!^2}\)
(b)
\(\frac{1}{2^n}\frac{2n!}{n!^2}\)
(c)
\(\frac{1}{2^n}2n!\)
(d)
\(\frac{1}{4^n}n!\)
Check Answer
Option a
Q.No:3 JEST-2013
A box contains \(100\) coins out of which \(99\) are fair coins and \(1\) is a double-headed coin. Suppose you choose a coin at random and toss it \(3\) times. It turns out that the results of all \(3\) tosses are heads. What is the probability that the coin you have drawn is the double-headed one?
(a)
\(0.99\)
(b)
\(0.925\)
(c)
\(0.075\)
(d)
\(0.01\)
Check Answer
Option c
Q.No:4 JEST-2015
If two ideal dice are rolled once, what is the probability of getting at least one `6'?
(a)
\(\frac{11}{36}\)
(b)
\(\frac{1}{36}\)
(c)
\(\frac{10}{36}\)
(d)
\(\frac{5}{36}\)
Check Answer
Option a
Q.No:5 JEST-2016
You receive on average \(5\) emails per day during a \(365\)-days year. The number of days on average on which you do not receive any emails in that year are:
(a)
More than \(5\)
(b) More than \(2\)
(c)
\(1\)
(d)
None of the above
Check Answer
Option b
Q.No:6 JEST-2016
A gas contains particles of type \(A\) with fraction \(0.8\), and particles of type \(B\) with fraction \(0.2\). The probability that among \(3\) randomly chosen particles at least one is of type \(A\) is:
(a)
\(0.8\)
(b)
\(0.25\)
(c)
\(0.33\)
(d)
\(0.992\)
Check Answer
Option d
Q.No:7 JEST-2017
Suppose that we toss two fair coins hundred times each. The probability that the same number of heads occur for both coins at the end of the experiment is
(a)
\(\left(\frac{1}{4}\right)^{100} \sum_{n=0}^{100} \begin{pmatrix}100\\n\end{pmatrix}\)
(b)
\(2\left(\frac{1}{4}\right)^{100} \sum_{n=0}^{100} \begin{pmatrix}100\\n\end{pmatrix}^2\)
(c)
\(\frac{1}{2}\left(\frac{1}{4}\right)^{100} \sum_{n=0}^{100} \begin{pmatrix}100\\n\end{pmatrix}^2\)
(d)
\(\left(\frac{1}{4}\right)^{100} \sum_{n=0}^{100} \begin{pmatrix}100\\n\end{pmatrix}^2\)
Check Answer
Option d
Q.No:8 JEST-2019
A person plans to go from town \(A\) to town \(B\) by taking either the route \((R1+R2)\) with probability \(1/2\) or the route \((R1+R3)\) with probability \(1/2\) (see figure). Further, there is a probability \(1/3\) that \(R1\) is blocked, a probability \(1/3\) that \(R2\) is blocked, and a probability \(1/3\) that \(R3\) is blocked. What is the probability that he/she would reach town \(B\)?

(a)
\(\frac{8}{9}\)
(b)
\(\frac{1}{3}\)
(c)
\(\frac{4}{9}\)
(d)
\(\frac{2}{3}\)
Check Answer
Option c
Q.No:9 JEST-2020
Ten persons named A, B, C, D, E, F, G, H, I, J have come for an interview. They are being called one by one to the interview panel at random. What is the probability that C gives interview before A and A gives before F?
(a)
\(1/6\)
(b)
\(1/10\)
(c)
\(1/8\)
(d)
\(1/4\)
Check Answer
Option a
Q.No:10 JEST-2020
If \(x\) and \(y\) have the joint probability distribution \(f(x, y)=3/4+xy\) for \(0<x, y<1\), and \(f(x, y)=0\) otherwise. What is the probability that \(y\) assumes a value greater than \(1/2\), given that \(x\) is equal to \(1/2\)
(a)
\(6/16\)
(b)
\(7/16\)
(c)
\(8/16\)
(d)
\(9/16\)
Check Answer
Option d
Q.No:11 JEST-2020
A particle is moving on a one-dimensional discrete lattice with lattice spacing unity. It can move from a site to its nearest neighbour site every \(1/5\) seconds with \(p\) being the probability to move right and \(q=(1-p)\) being the probability to move left. Consider that the particle starts at origin, \(x=0\) at time \(t=0\). Taking \(p=3/4\), calculate the variance \(\langle (x-\langle x\rangle)^2\rangle\) at time \(t=5\times 10^4\) seconds, where \(\langle x\rangle\) is the average position.
Check Answer
Ans 7500
Q.No:12 JEST-2021
The six faces of a cube are painted violet, blue, red, green, yellow, and orange. If the cube is rolled \(4\) times, what is the probability that the green face appears exactly \(3\) times?
(a)
\(3/24\)
(b)
\(5/124\)
(c)
\(5/324\)
(d)
\(15/222\)
Check Answer
Option c
Q.No:13 JEST-2022
The probability that you get a sum \(m\) from a throw of two identical fair dice is \(P_m\). If the dice have \(6\) (six) faces labeled by \(1, 2, ... 6\), which of the following statements is correct?
(a)
\(P_9=P_5\)
(b)
\(P_9=P_4\)
(c)
\(P_9=P_3\)
(d)
\(P_9=P_6\)
Check Answer
Option a
Q.No:14 JEST-2023
Two fair six-faced dice are thrown simultaneously. The probability that one of the dice yields an outcome that is a multiple of 2 and the other yields a multiple of 3 is:
(a) \(\frac{1}{6}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{13}{16}\)
(d) \(\frac{11}{36}\)
Check Answer
Option d
Q.No:1 TIFR-2015
A random number generator outputs \(+1\) or \(-1\) with equal probability every time it is run. After it is run \(6\) times, what is the probability that the sum of the answers generated is zero? Assume that the individual runs are independent of each other.
(a)
\(1/2\)
(b)
\(5/6\)
(c)
\(5/16\)
(d)
\(15/32\)
Check Answer
Option c
Q.No:2 TIFR-2016
In a triangular lattice a particle moves from a lattice point to any of its \(6\) neighbouring points with equal probability, as shown in the figure on the right.
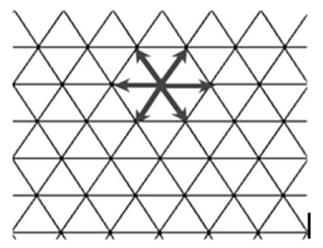
The probability that the particle is back at its starting point after \(3\) moves is
(a)
\(5/18\)
(b)
\(1/6\)
(c)
\(1/18\)
(d)
\(1/36\)
Check Answer
Option c
Q.No:3 TIFR-2019
A British coin has a portrait of Queen Elizabeth II on the `heads' side and `ONE POUND' written on the `tails' side, while an Indian coin has a portrait of Mahatma Gandhi on the `heads' side and `10 RUPEES' written on the `tails' side (see below).

These two coins are tossed simultaneously twice in succession.
The result of the first toss was `heads' for both the coins. The probability that the result of the second toss had a `10 RUPEES' side is
(a)
\(1/2\)
(b)
\(4/7\)
(c)
\(3/5\)
(d)
\(2/3\)
Check Answer
Option b
Q.No:4 TIFR-2021
In a country, the fraction of population infected with Covid-19 is \(0.2\). It is also known that out of the people who are infected with Covid-19, only a fraction \(0.3\) show symptoms of the disease, while the rest do not show any symptoms. If you randomly select a citizen of this country, the probability that this person will \({\bf NOT}\) show symptoms of Covid-19 is
(a)
\(0.94\)
(b)
\(0.56\)
(c)
\(0.86\)
(d)
\(0.80\)
Check Answer
Option a
Q.No:5 TIFR-2022
In a standardized entrance exam, the passing rates for the past 10 years are tabulated below.

If 1000 candidates appear for the exam every year, the probability that more than 250 students will pass the exam this year is about
(a)
\(6\%\)
(b)
\(20\%\)
(c)
\(25\%\)
(d)
\(0.1\%\)
Check Answer
Option a
Q.No:6 TIFR-2024
A student measures the radioactive decay of a material with a half-life of 13,000 years with a Geiger counter. In the laboratory notebook, the student records the following number of decays every 10 seconds:
158, 146, 145, 163, 154, 163, 160, 160, 152, 157, 154, 156, 149, 168, 152
The teacher suspects that the experiment was not done properly and the student created the numbers manually. Why would the teacher have such a suspicion?
158, 146, 145, 163, 154, 163, 160, 160, 152, 157, 154, 156, 149, 168, 152
The teacher suspects that the experiment was not done properly and the student created the numbers manually. Why would the teacher have such a suspicion?
(a) The variance is much less than the mean, unlike what is expected for a Poisson distribution.
(b) The standard deviation is much less than the variance, as expected for a Poisson distribution.
(c) The median is less than the mean, unlike what is expected for a Poisson distribution.
(d) The median is greater than the mean, as expected for a Poisson distribution.
Check Answer
Option a
Q.No:7 TIFR-2025
For a given measurement of particles in a counter, a 10-minute data collection resulted in a statistical uncertainty of 2.5%. How much additional time must be allocated to reduce the statistical uncertainty to 0.5%?
a) 240 minutes
b) 40 minutes
c) 250 minutes
d) 50 minutes
Check Answer
Option a
Q.No:8 TIFR-2025
Consider a random walker on a 2D plane which starts at the origin. At every step it either moves one unit along the positive x-axis with probability 1/2 or along the positive y-axis with probability 1/2. The distance from the origin after n steps is denoted by \(r_n.\) What is the mean square displacement \(⟨r_n^2⟩\)?
a) \(n(n + 1)/2\)
b) \(n(n – 1)/2\)
c) \(n^2\)
d) \(n(n – 1)\)
Check Answer
Option a
Q.No:9 TIFR-2025
Consider two random variables \(x\) and \(y\) described by the joint distribution
\[
P(x,y)=\frac{1}{2\pi \sqrt{1-a^{2}}}
\exp\left(\frac{2axy - x^{2} - y^{2}}{2(1-a^{2})}\right),
\]
with \(0<a<1\).
If the above distribution is written in terms of orthogonal coordinates
\(z = x - y\) and \(u = x + y\),
the probability distribution in \(z\) is given by:
a) A Gaussian with mean \(0\) and standard deviation \(\sqrt{2(1-a)}\)
b) A Gaussian with mean \(\sqrt{a}\) and standard deviation \(\sqrt{2(1-a)}\)
c) A Gaussian with mean \(0\) and standard deviation \(\sqrt{2(1-a^{2})}\)
d) Not a Gaussian distribution
Check Answer
Option a
Q.No:10 TIFR-2025
Consider a particle \(P\) moving on a one-dimensional discrete lattice with lattice constant \(a\). \(P\) can hop from one site to a neighbouring site. The probabilities of moving to the right and left are \(p\) and \(q = 1 - p\), respectively. Starting from the origin \(x = 0\) at time \(t = 0\), what is the mean square displacement \(\langle (x - \langle x\rangle)^{2}\rangle\) after \(N\) steps, where \(\langle x\rangle\) is the average position at time \(t\)?
a) \(4 N a^{2} p q\)
b) \(4 N a^{2} (p - q)\)
c) \(2 N a^{2} p q\)
d) \(2 N a^{2} (p - q)\)
Check Answer
Option a
Q.No:11 TIFR-2025
Two students perform a counting experiment independently. Student A measures the counts for 1-minute intervals each and repeats the measurement five times. The obtained counts are give below
\[
\begin{array}{c|c}
\text{Measurement turn} & \text{Counts} \\ \hline
1 & 25 \\
2 & 35 \\
3 & 30 \\
4 & 23 \\
5 & 27 \\
\end{array}
\]
This student then takes the mean of these counts and reports the count rate (counts/min). The second student (B) makes one measurement for five minutes. She measures 145 counts and reports the count rate (counts/min). If the clock used for all these measurements is accurate up to 0.1 minutes, and there are no other sources of uncertainties, we can conclude that:
a) The count rate reported by student A will have a larger uncertainty than that reported by student B.
b) The count rate reported by student B will have a larger uncertainty than that reported by student A.
c) The reported uncertainty in both results would be identical.
d) Nothing may be concluded about the relative uncertainties between A and B.
