Q.No:1 JAM-2015
A particle with energy \(E\) is incident on a potential given by
\[
V(x)=
\left\{
\begin{array}{ll}
0 & \text{for } x<0 \\
V_0 & \text{for } x \geq 0
\end{array}
\right.
\].
The wave function of the particle for \(E\) \(< \)\(V_0\) , in the region \(x \gt 0\) (in the terms of positive constants A, B and k) is
(A)
\(A \hspace{0.5mm}e^{kx}+B \hspace{0.5mm}e^{-kx}\)
(B)
\(A \hspace{0.5mm}e^{-kx}\)
(C)
\(A \hspace{0.5mm}e^{ikx}+B \hspace{0.5mm}e^{-ikx}\)
(D)
Zero
Check Answer
Option B
Q.No:2 JAM-2015
A particle is moving in a two-dimensional potential well
\[V(x,y)=
\left\{
\begin{array}{ll}
0,& 0\leq x\leq L ,0\leq y \leq 2L \\
\infty , & Otherwise
\end{array}
\right.\]
Which of the following statements about the ground state energy \(E_1\) and ground state eigenfunction \(\varphi_0 \) are true?
(A)
\(E_1=\frac{\hbar^2 \pi^2}{mL^2}\)
(B)
\(E_1=\frac{5\hbar^2 \pi^2}{8mL^2}\)
(C)
\(\varphi_0=\frac{\sqrt{2}}{L}\hspace{1mm} sin \hspace{1mm} \frac{\pi x}{L} \hspace{1mm} sin \hspace{1mm}\frac{\pi y}{2L}\)
(D)
\(\varphi_0=\frac{\sqrt{2}}{L}\hspace{1mm} cos\hspace{1mm} \frac{\pi x}{L}\hspace{1mm} cos \hspace{1mm}\frac{\pi y}{2L}\)
Check Answer
Option B,C
Q.No:3 JAM-2015
A particle is in a state which is a superposition of the ground state \(\varphi_0\) and the first excited state \(\varphi_1\) of a one-dimensional quantum harmonic oscillator. The state is given by \(\Phi= \frac{1}{\sqrt{5}}\varphi_0+\frac{2}{\sqrt{5}}\varphi_1\). The expectation value of the energy of the particle in this state (in units of \(\hbar \omega\), \(\omega\) being the frequency of the oscillator is __________________.
Check Answer
Ans 1.3
Q.No:4 JAM-2016
A free particle of energy \(E\) collides with a one-dimensional square potential barrier of height \(V\) and width \(W\). Which one of the following statement(s) is(are) correct?
(A)
For \(E>V\), the transmission coefficient for the particle across the barrier will always be unity.
(B)
For \(E<V\), the transmission coefficient changes more rapidly with \(W\) than with \(V\).
(C)
For \(E<V\), if \(V\) is doubled, the transmission coefficient will also be doubled.
(D)
Sum of the reflection and the transmission coefficients is always one.
Check Answer
Option B,D
Q.No:5 JAM-2016
The de Broglie wavelength of a relativistic electron having 1 MeV of energy is _____________ \(\times 10^{-12}\)m.
(Take the rest mass energy of the electron to be 0.5 MeV. Planck constant=\(6.63 \times 10^{-34}\)Js,Speed of
light=\(3\times 10^8\)m/s, Electronic charge =\(1.6\times 10^{-19}\)C)
Check Answer
Ans 1.3-1.6
Q.No:6 JAM-2017
For the three matrices given below, which one of the choices is correct?
\(\sigma_1=
\begin{pmatrix} 0&1\\ 1&0 \end{pmatrix}\) \hspace{4mm} \(\sigma_2=\begin{pmatrix} 0&i\\ -i&0 \end{pmatrix}\) \hspace{4mm} \(\sigma_3=\begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix}
\)
(A)
\(\sigma_1\sigma_2=-i\sigma_3\)
(B)
\(\sigma_1\sigma_2=i\sigma_3\)
(C)
\(\sigma_1\sigma_2+\sigma_2\sigma_1=I\)
(D)
\(\sigma_3\sigma_2=-i\sigma_1\)
Check Answer
Option A
Q.No:7 JAM-2017
A photon of frequency \(v\) strikes an electron of mass \(m\) initially at rest. After scattering at an angle \(\phi\), the photon loses half of its energy. If the electron recoils at an angle \(\theta\), which of the following is (are) true?
(A)
\(cos \hspace{1mm}\phi=(1-\frac{mc^2}{hv})\)
(B)
\(sin \hspace{1mm}\phi=(1-\frac{mc^2}{hv})\)
(C)
The ratio of the magnitudes of momenta of the recoiled electron and scattered photon is \(\frac{sin \hspace{0.5mm}\phi}{sin \hspace{0.5mm}\theta}\)
(D)
Change in photon wavelength is \(\frac{h}{mc}(1-2 \hspace{0.5mm} cos \hspace{0.5mm}\phi)\)
Check Answer
Option A,C
Q.No:8 JAM-2017
For a proton to capture an electron to form a neutron and a neutrino (assumed massless), the electron must have some minimum energy. For such an electron the de Broglie wavelength in pictometers is ____________.
(Specify your answer to two digits after the decimal point)
Check Answer
Ans 1.0-1.10
Q.No:9 JAM-2018
Consider two waves \(y_1=a \hspace{1mm} cos (\omega t-kz)\) and \(y_2=a \hspace{1mm} cos [(\omega +\Delta \omega)t-(k+\Delta k)z]\). The group velocity of the superposed wave will be (\(\Delta \omega \ll \omega\) and \(\Delta k \ll k\))
(A)
\(\frac{(\omega-\Delta \omega)}{(k-\Delta k)}\)
(B)
\(\frac{(2\omega+\Delta \omega)}{(2k+\Delta k)}\)
(C)
\(\frac{\Delta \omega}{\Delta k}\)
(D)
\(\frac{(\omega+\Delta \omega)}{(k+\Delta k)}\)
Check Answer
Option C
Q.No:10 JAM-2018
A particle of mass \(m\) is in a one dimensional potential \(V(x)=\left\{
\begin{array}{ll}
0 & , 0<x<L \\
\infty & , otherwise
\end{array}
\right.\)
At some instant its wave function is given by
\(\psi(x)=\frac{1}{\sqrt{3}}\psi_1(x)+i \sqrt{\frac{2}{3}}\psi_2(x)\), where \(\psi_1(x)\) and \(\psi_2(x)\) are the ground and the first excited states, respectively. Identify the correct statement.
(A)
\(\langle x\rangle=\frac{L}{2} ; \langle E\rangle=\frac{\hbar ^2}{2m}\frac{3\pi^2}{L^2}\)
(B)
\(\langle x\rangle=\frac{2L}{3} ; \langle E\rangle=\frac{\hbar ^2}{2m}\frac{\pi^2}{L^2}\)
(C)
\(\langle x\rangle=\frac{L}{2} ; \langle E\rangle=\frac{\hbar ^2}{2m}\frac{8\pi^2}{L^2}\)
(D)
\(\langle x\rangle=\frac{2L}{3} ; \langle E\rangle=\frac{\hbar ^2}{2m}\frac{4\pi^2}{3L^2}\)
Check Answer
Option A
Q.No:11 JAM-2019
For a quantum particle confined inside a cubic box of side \(L\), the ground state energy is given by \(E_0\). The energy of the first excited state is
(A)
\(2E_0\)
(B)
\(\sqrt{2}E_0\)
(C)
\(3E_0\)
(D)
\(6E_0\)
Check Answer
Option A
Q.No:12 JAM-2019
A \(\gamma\)-ray y photon emitted from a \(^{137}Cs\) source collides with an electron at rest. If the Compton shift of the photon is \(3.25\times 10^{-13}\)m, then the scattering angle is closest to
(Planck’s constant \(h=6.626\times 10^{-34}\)J s, electron mass \(m_e=9.109\times 10^{-31}\)kg and velocity of light in free space \(c=3\times 10^8\)m/s.)
(A)
\(45^\circ\)
(B)
\(60^\circ\)
(C)
\(30^\circ\)
(D)
\(90^\circ\)
Check Answer
Option C
Q.No:13 JAM-2019
Given the wave function of a particle \(\psi(x)=\sqrt{\frac{2}{L}} sin (\frac{\pi}{L} x)\) for \(0<x<L\) and 0 elsewhere,the probability of finding the particle between \(x = 0\) and \(x =L/2\) is ______________ .
(Round off to 1 decimal place)
Check Answer
Ans 0.50
Q.No:14 JAM-2020
In a photoelectric effect experiment, a monochromatic light source emitting photons with energy greater than the work function of the metal under test is used. If the power of the light source is doubled, which one of the following statements is correct?
(A)
The number of emitted photoelectrons remains the same.
(B)
The stopping potential remains the same.
(C)
The number of emitted photoelectrons decreases.
(D)
The stopping potential doubles
Check Answer
Option B
Q.No:15 JAM-2020
Consider the motion of a quantum particle of mass \(m\) and energy \(E\) under the influence of a step potential of height \(V_0\). If \(R\) denotes the reflection coefficient, which one of the following statements
is true?
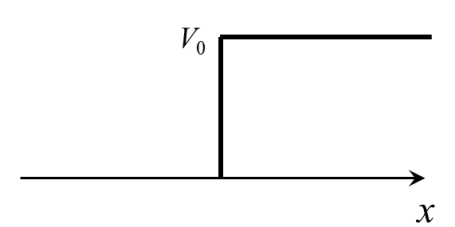
(A)
If \(E=\frac{4}{3}V_0 , R=1\)
(B)
If \(E=\frac{4}{3}V_0 , R=0\)
(C)
If \(E=\frac{1}{2}V_0 , R=1\)
(D)
If \(E=\frac{1}{2}V_0 , R=0.5\)
Check Answer
Option C
Q.No:16 JAM-2020
The normalized ground-state wave function of a one-dimensional quantum harmonic oscillator with force constant \(k\) and mass \(m\) is \(\psi_0(x)=(\frac{\alpha}{\pi})^{1/4}e^{-\alpha x^2/2}\) , where \(\alpha=m \omega_0 /\hbar \) and \(\omega_0 ^2=K/m\). Which one of the following is the probability of finding the particle outside the classically allowed region?
(The classically allowed region is where the total energy is greater than the potential energy)
(A)
\(\frac{2}{\sqrt{\pi}}\int_1 ^\infty y^2 e^{-y^2} dy \)
(B)
\(\frac{2}{\sqrt{\pi}}\int_1 ^\infty e^{-y^2} dy \)
(C)
\(0.5\)
(D)
\(0\)
Check Answer
Option B
Q.No:17 JAM-2020
A linear operator \(\hat{O}\) acts on two orthonormal states of a system \(\psi_1\) and \(\psi_2\) as per following: \(\hat{O}\psi_1=\psi_2\) , \(\hat{O}\psi_2=\frac{1}{\sqrt{2}}(\psi_1 + \psi_2)\). The system is in a superposed state defined by \(\psi =\frac{1}{\sqrt{2}} \psi_1 +\frac{i}{\sqrt{2}}\psi_2 \). The expectation value of \(\hat{O}\) in the state \(\psi\) is
(A)
\(\frac{1}{2\sqrt{2}}(1+i(\sqrt{2}+1))\)
(B)
\(\frac{1}{2\sqrt{2}}(1-i(\sqrt{2}+1))\)
(C)
\(\frac{1}{2\sqrt{2}}(1+i(\sqrt{2}-1))\)
(D)
\(\frac{1}{2\sqrt{2}}(1-i(\sqrt{2}-1))\)
Check Answer
Option D
Q.No:18 JAM-2020
Consider a one-dimensional infinite potential well of width \(a\). This system contains five non-interacting electrons, each of mass \(m\), at temperature T= 0 K. The energy of the highest occupied state is
(A)
\(\frac{25\pi^2 \hbar^2}{2ma^2}\)
(B)
\(\frac{10\pi^2 \hbar^2}{2ma^2}\)
(C)
\(\frac{5\pi^2 \hbar^2}{2ma^2}\)
(D)
\(\frac{9\pi^2 \hbar^2}{2ma^2}\)
Check Answer
Option D
Q.No:20 JAM-2020
Two transverse waves \(y_1=5 \hspace{1mm} cos(kx-\omega t)\)cm, and \(y_2=5 \hspace{1mm} cos(kx+\omega t)\)cm, travel on a string
along x-axis. If the speed of a point at \(x=0\) is zero at \(t=0\)s, 0.25 s and 0.5 s, then the minimum frequency of the waves is __________ Hz.
Check Answer
Ans 2
Q.No:21 JAM-2021
Identify the correct statement(s) regarding nuclei
(A)
The uncertainty in the momentum of a proton in a nucleus is roughly \(10^5\) times the uncertainty in the momentum of the electron in the ground state of Hydrogen atom
(B)
The volume of a nucleus grows linearly with the number of nucleons in it
(C)
The energy of \(\gamma\) rays due to de-excitation of a nucleus can be of the order of MeV
(D)
\(^{56} Fe\) is the most stable nucleus
Check Answer
Option A,B,C OR A,B,C,D
Q.No:22 JAM-2021
A particle of mass \(m\) is in an infinite square well potential of length \(L\). It is in a superposed state of the first two energy eigenstates, as given by \(\psi(x)=\frac{1}{\sqrt{3}}\psi_{n=1}{(x)}+\sqrt{\frac{2}{3}}\psi_{n=2}{(x)}\). Identify the correct statement(s). \(h\) is Planck’s constant.
(A)
\(\langle p \rangle =0\)
(B)
\(\Delta p=\frac{\sqrt{3}h}{2L}\)
(C)
\(\langle E \rangle=\frac{3h^2}{8mL^2}\)
(D)
\(\Delta x=0\)
Check Answer
Option A,B,C
Q.No:23 JAM-2021
An ideal blackbody at temperature \(T\), emits radiation of energy density \(u\). The corresponding value for a material at temperature \(\frac{T}{2}\) is \(\frac{u}{256}\). Its emissivity is ________________ (Round off to three decimal places).
Check Answer
Ans 0.060-0.065
Q.No:24 JAM-2021
Twenty non-interacting spin \(1/2\) particles are trapped in a three-dimensional simple harmonic oscillator potential of frequency \(\omega\). The ground state energy of the system, in units of \(\hbar \omega\), is ____________ .
Check Answer
Ans 60
Q.No:25 JAM-2022
Consider a particle trapped in a three-dimensional potential well such that \(U(x,y,z)=0\) for \(0 \leq x \leq a\), \(0\leq y \leq a\) , \(0 \leq z \leq a\) and \(U(x,y,z)=\infty\) everywhere else. The degeneracy of the \(5^{th}\) excited state is
(A)
1
(B)
3
(C)
6
(D)
9
Check Answer
Option C
Q.No:26 JAM-2022
Consider a quantum particle trapped in a one-dimensional potential well in the region \([-L/2 <x<L/2]\),with infinitely high barriers at \(x=-L/2\) and \(x=L/2\). The stationary wave function for the ground state is \(\psi(x)=\sqrt{\frac{2}{L}} cos (\frac{\pi x}{L})\). The uncertainties in momentum and position satisfy
(A)
\(\Delta p=\frac{\pi \hbar}{L}\) and \(\Delta x=0\)
(B)
\(\Delta p=\frac{2\pi \hbar}{L}\) and \(0<\Delta x< \frac{L}{2\sqrt{3}}\)
(C)
\(\Delta p=\frac{\pi \hbar}{L}\) and \(\Delta x>\frac{L}{2\sqrt{3}}\)
(D)
\(\Delta p=0\) and \(\frac{L}{2}\)
Check Answer
Option MTA
Q.No:27 JAM-2022
The dispersion relation for certain type of waves is given by \(\omega = \sqrt{k^2 + a^2}\), where \(k\) is the wave vector and \(a\) is a constant. Which one of the following sketches represents \(v_g\), the group velocity?

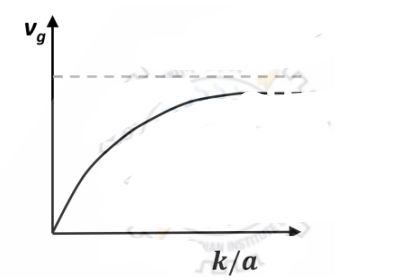

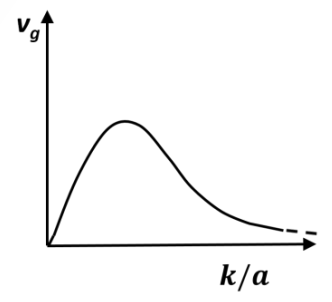
Check Answer
Option B
Q.No:28 JAM-2022
In the Compton scattering of electrons, by photons incident with wavelength \(\lambda\),
(A)
\(\frac{\Delta \lambda}{\lambda}\) is independent of \(\lambda\)
(B)
\(\frac{\Delta \lambda}{\lambda}\) increases with decreasing \(\lambda\)
(C)
there is no change in photon’s wavelength for all angles of deflection of the photon
(D)
\(\frac{\Delta \lambda}{\lambda}\) increases with increasing angle of deflection of the photon
Check Answer
Option B,D
Q.No:29 JAM-2022
Consider an electron with mass \(m\) and energy \(E\) moving along the x-axis towards a finite step potential of height \(U_0\) as shown in the figure. In region \(1\) \((x<0)\), the momentum of the electron is \(p_1=\sqrt{2mE}\). The reflection coefficient at the barrier
is given by \(R=(\frac{p_1-p_2}{p_1 +p_2})^2\), where \(p_2\) is the momentum in region \(2\). If, in the limit \(E \gg U_0 ,R \approx \frac{U_0 ^2}{nE^2}\), then the integer \(n\) is _______________ .
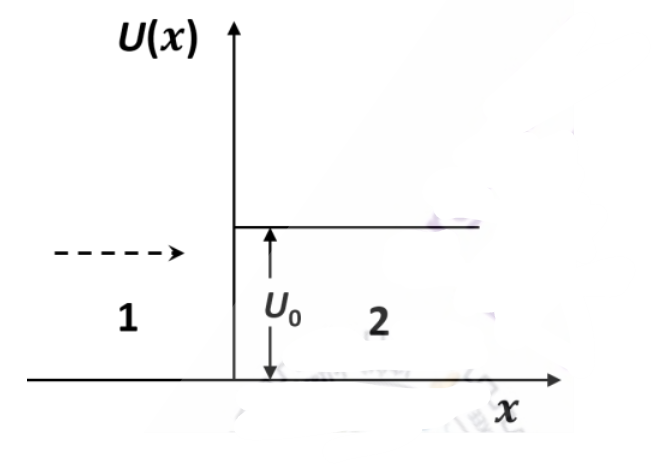
Check Answer
Ans 16
Q.No:30 JAM-2017
Consider a one-dimensional harmonic oscillator of angular frequency \(\omega\). If 5 identical particles occupy the energy levels of this oscillator at zero temperature, which of the
following statement(s) about their ground state energy \(E_0\) is (are) correct?
(A)
If the particles are electrons, \(E_0=\frac{13}{2}\hbar \omega\)
(B)
If the particles are protons,\(E_0=\frac{25}{2}\hbar \omega\)
(C)
If the particles are spin-less fermions,\(E_0=\frac{25}{2}\hbar \omega\)
(D)
If the particles are bosons,\(E_0=\frac{5}{2}\hbar \omega\)
Check Answer
Option A,C,D
Q.No:31 JAM-2016
X-rays of 20 keV energy is scattered inelastically from a carbon target. The kinetic energy transferred to the recoiling electron by photons scattered at \(90^\circ\) with respect to the incident beam is ___________________ keV
(Planck constant =\(6.6\times 10^{-34}\) Js, Speed of light= \(3\times 10^8\) m/s, electron mass =\(9.1\times 10^{-31}\) kg,Electronic charge =\(1.6\times 10^{-19}\)C)
Check Answer
Ans 0.68-0.82
Q.No:32 JAM-2017
A particle of mass \(m\) is placed in a three-dimensional cubic box of side \(a\) . What is the degeneracy of its energy level with energy \(14(\frac{\hbar^2 \pi^2}{2ma^2})\) ?
(Express your answer as an integer)
Check Answer
Ans 6
Q.No:33 JAM-2023
If the ground state energy of a particle in an infinite potential well of width \(L_1\) is equal to the energy of the second excited state in another infinite potential well of width \(L_2\), then the ratio \(\frac{L_1}{L_2}\) is equal to
A) \(1\)
B) \(1/3\)
C) \(1/\sqrt{3}\)
D) \(1/9\)
Check Answer
Option B
Q.No:34 JAM-2023
The phase velocity \(v_p\) of transverse waves on a one-dimensional crystal of atomic separation \(d\) is related to the wavevector \(k\) as
\[v_p=C \hspace{0.5mm} \frac{sin (kd/2)}{(kd/2)}\]
The group velocity of these waves is
A) \(C \hspace{0.5mm}[cos(kd/2)-\frac{sin(kd/2)}{(kd/2)}]\)
B) \(C \hspace{0.5mm} cos(kd/2)\)
C) \(C \hspace{0.5mm}[cos(kd/2)+\frac{sin(kd/2)}{(kd/2)}]\)
D)\(C \hspace{0.5mm}\frac{sin(kd/2)}{(kd/2)}\)
Check Answer
Option B
Q.No:35 JAM-2023
The spectral energy density \(u_T (\lambda)\) vs wavelength (\(\lambda\)) curve of a black body shows a peak at \(\lambda=\lambda_{max}\). If the temperature of the black body is doubled, then
A) the maximum of \(u_T (\lambda)\) shifts to \(\lambda_{max}/2\)
B) the maximum of \(u_T (\lambda)\) shifts to \(2\lambda_{max}\)
C) the area under the curve becomes 16 times the original area
D) the area under the curve becomes 8 times the original area
Check Answer
Option A,C
Q.No:36 JAM-2023
The state of a harmonic oscillator is given as \(\psi= \frac{1}{\sqrt{3}}\psi_0-\frac{1}{\sqrt{6}}\psi_1+\frac{1}{\sqrt{2}}\psi_2\) , where \(\psi_0,\psi_1\) and \(\psi_2\) are the normalized wave functions of ground, first excited, and second excited states, respectively. Which of the following statement(s) is/are true?
A) A measurement of the energy of the system yields \(E=\frac{1}{2} \hbar \omega\) with non-zero probability
B) A measurement of the energy of the system yields \(E=\frac{5}{3} \hbar \omega\) with non-zero probability
C) Expectation value of the energy of the system \(\langle E \rangle=\frac{5}{3} \hbar \omega\)
D) Expectation value of the energy of the system \(\langle E \rangle=\frac{7}{6} \hbar \omega\)
Check Answer
Option A,C
Q.No:37 JAM-2023
In a X-Ray tube operating at 20 kV, the ratio of the de-Broglie wavelength of the incident electrons to the shortest wavelength of the generated X-rays is _________ (rounded off to two decimal places).
Given: e/m ratio for an electron = 1.76\(\times 10^{11}\) Ck\(g^{-1}\)
and the speed of light in vacuum is \(3 \times 10^8\) m\(s^{-1}\)
Check Answer
Ans 0.12-0.16
Q.No:38 JAM-2023
A point source emitting photons of 2 eV energy and 1 W of power is kept at a distance of 1m from a small piece of a photoelectric material of area \(10^{-4} m^2\). If the efficiency of generation of photoelectrons is \(10\%\), then the number of photoelectrons generated are \(f \times 10^{12}\) per second. The value of \(f\) is_____________________ (rounded off to two decimal places).
Given: 1eV = \(1.6 \times 10^{-19} J\)
Check Answer
Ans 2.30-2.70
Q.No:39 JAM-2023
In the Thomson model of hydrogen atom, the nuclear charge is distributed
uniformly over a sphere of radius \(R\). The average potential energy of an electron confined within this atom can be taken as \(V=-\frac{e^2}{4 \pi \epsilon_0 R}\). Taking the uncertainty in position to be the radius of the atom, the minimum value of \(R\) for which an electron will be confined within the atom is estimated to be \(f \times 10^{-11}\) m. The value of \(f\) is ____________________________(rounded off to one decimal place).
Given: The uncertainty product of momentum and position is \(\hbar = 1\times 10^{-34}\) J\(s\), \(e=1.6 \times 10^{-19}\) C, and \(\frac{1}{4\pi \epsilon_0 }=9 \times 10^9 N m^2 C^{-2}\)
Check Answer
Ans 2.2-2.7
Q.No:40 JAM-2024
Which of the following matrices is Hermitian as well as unitary?
A) \(\begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}\)
B) \(\begin{pmatrix} 0 & i \\ i & 0 \end{pmatrix}\)
C) \(\begin{pmatrix} 1 & -i \\ i & 1 \end{pmatrix}\)
D) \(\begin{pmatrix} 0 & 1+i \\ 1-i & 0 \end{pmatrix}\)
Check Answer
Option A
Q.No:41 JAM-2024
The magnitudes of spin magnetic moments of electron, proton and neutron are \(\mu_e\), \(\mu_p\) and \(\mu_n\), respectively. Then,
A) \(\mu_e > \mu_p > \mu_n\)
B) \(\mu_e = \mu_p > \mu_n\)
C) \(\mu_e < \mu_p < \mu_n\)
D) \(\mu_e < \mu_p = \mu_n\)
Check Answer
Option A
Q.No:42 JAM-2024
A particle moving along the x-axis approaches \(x = 0\) from \(x = -\infty\) with a total energy \(E\). It is subjected to a potential \(V(x)\). For time \(t \rightarrow \infty\), the probability density \(P(x)\) of the particle is schematically shown in the figure.
The correct option for the potential \(V(x)\) is:
The correct option for the potential \(V(x)\) is:
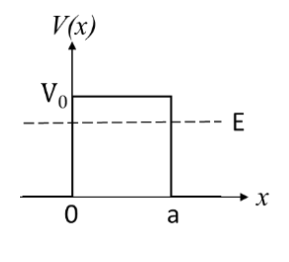
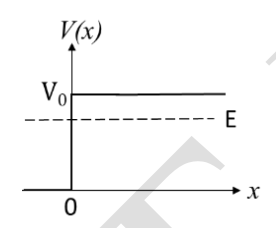
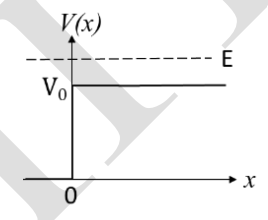
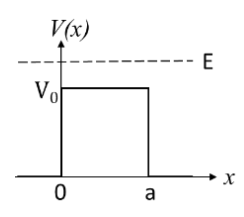
Check Answer
Option C
Q.No:43 JAM-2024
The ultraviolet catastrophe in the classical (Rayleigh-Jeans) theory of cavity radiation is attributed to the assumption that
A) the standing waves of all allowed frequencies in the cavity have the same average energy
B) the density of the standing waves in the cavity is independent of the shape and size of the cavity
C) the allowed frequencies of the standing waves inside the cavity have no upper limit
D) the number of allowed frequencies for the standing waves in a frequency range \(v\) to \(v + dv\) is proportional to \(v^2\)
Check Answer
Option A
Q.No:44 JAM-2024
A one-dimensional infinite square-well potential is given by:
\[ V(x) =
\begin{cases}
0 & \text{for } -\frac{a}{2} < x < \frac{a}{2} \\
\infty & \text{elsewhere}
\end{cases}
\]
Let \(E_e(x)\) and \(\psi_e(x)\) be the ground state energy and the corresponding wave function, respectively, if an electron (\(e\)) is trapped in that well. Similarly, let \(E_\mu(x)\) and \(\psi_\mu(x)\) be the corresponding quantities, if a muon (\(\mu\)) is trapped in the well. Choose the correct option:
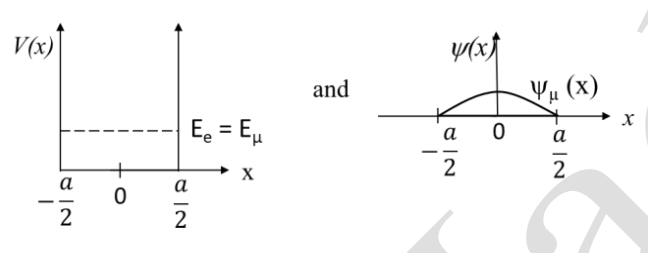
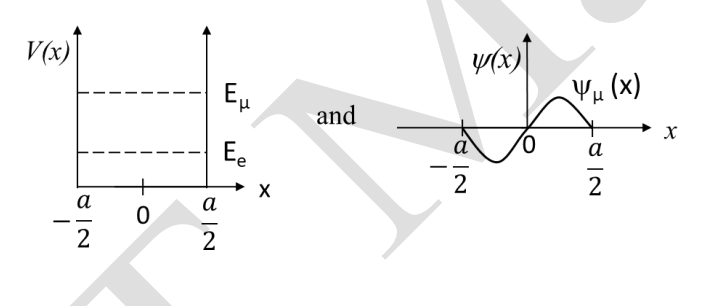

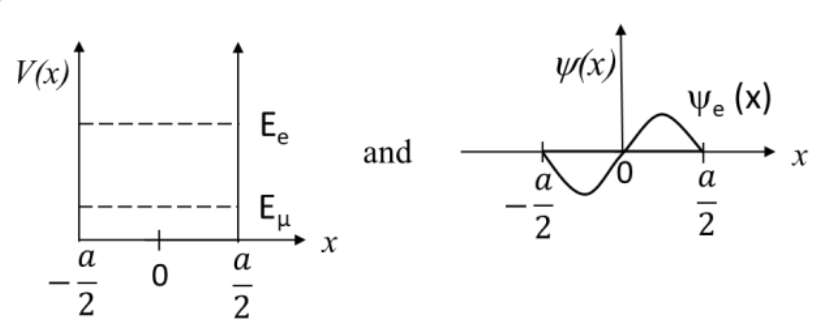
Check Answer
Option C
Q.No:45 JAM-2024
Consider two different Compton scattering experiments, in which X-rays and \( \gamma \)-rays of wavelength (\( \lambda \)) 1.024Å and 0.049Å, respectively, are scattered from stationary free electrons. The scattered wavelength (\( \lambda' \)) is measured as a function of the scattering angle (\( \theta \)). If Compton shift is \( \Delta\lambda = \lambda' - \lambda \), then which of the following statement(s) is/are true:
\( h = 6.63 \times 10^{-34}Js, m_e = 9.11 \times 10^{-31}kg, c = 3 \times 10^8m/s \)
A) For \( \gamma \)-rays, \( \lambda'_{\text{max}} \approx 0.098Å \)
B) For X-rays, \( (\Delta\lambda)_{\text{max}} \) is observed at \( \theta = 180^\circ \)
C) For X-rays, \( (\Delta\lambda)_{\text{max}} \approx 1.049Å \)
D) For \( \gamma \)-rays, at \( \theta = 90^\circ \), \( \lambda' \approx 0.049Å \)
Check Answer
Option A,B
Q.No:46 JAM-2025
At a particular temperature \(T\), Planck’s energy density of black body radiation in terms of frequency is
\(\rho_T(\nu) = 8 \times 10^{-18}\, \frac{J/m^3}{Hz}\)
at \(\nu = 3 \times 10^{14}\, Hz\).
Then Planck’s energy density \(\rho_T(\lambda)\) at the corresponding wavelength \(\lambda\) has the value \(\underline{\hspace{1.5cm}} \times 10^{2}\, \frac{J/m^3}{m}\) (in integer).
\([ \text{Speed of light } c = 3 \times 10^{8}\, m/s ]\)
Then Planck’s energy density \(\rho_T(\lambda)\) at the corresponding wavelength \(\lambda\) has the value \(\underline{\hspace{1.5cm}} \times 10^{2}\, \frac{J/m^3}{m}\) (in integer).
\([ \text{Speed of light } c = 3 \times 10^{8}\, m/s ]\)
Check Answer
ANS 24
Q.No:47 JAM-2025
For a non-relativistic free particle, the ratio of phase velocity to group velocity is
A) 2
B) \(\frac{1}{2}\)
C) 1
D) \(\frac{1}{4}\)
Check Answer
Option B
Q.No:48 JAM-2025
A particle of mass \(m\) is subjected to a potential \(V(x)\).
Its wavefunction is given by
\[
\psi(x,t)=\alpha x^{2} e^{-\beta x} e^{i\gamma t/\hbar}, \quad x>0,
\]
\[
\psi(x,t)=0, \quad x\le 0.
\]
(\(\alpha,\ \beta,\ \gamma\) are constants of appropriate dimensions.)
Then \(V(x)\) is
A) \(
-\gamma + \frac{\hbar^{2}}{2m}
\left(
\frac{2}{x^{2}} - \frac{4\beta}{x} + \beta^{2}
\right)
\)
B) \(
-\gamma + \frac{\hbar^{2}}{2m}
\left(
\frac{2}{x^{2}} + \frac{4\beta}{x} + \beta^{2}
\right)
\)
C) \(
-\gamma + \frac{\hbar^{2}}{2m}
\left(
\frac{2}{x^{2}} - \frac{4\beta}{x} - \beta^{2}
\right)
\)
D) \(
-\gamma + \frac{\hbar^{2}}{2m}
\left(
-\frac{2}{x^{2}} - \frac{4\beta}{x} + \beta^{2}
\right)
\)
Check Answer
Option A
Q.No:49 JAM-2025
Neutrons of energy \(8~\text{MeV}\) are incident on a potential step of height
\(48~\text{MeV}\). As they penetrate the classically forbidden region, the distance
at which the probability density of finding neutrons decreases by a factor of 100 is
_____ fm (up to two decimal places).
(Take \(\hbar c = 200~\text{MeV·fm}\), and the rest mass energy of neutron
\(= 1~\text{GeV}\).)
Check Answer
ANS 1.55 to 1.70
Q.No:50 JAM-2025
Identify which of the following wave functions describe(s) travelling wave(s).
(\(A_0, B_0, a,\) and \(b\) are positive constants of appropriate dimensions)
A) \(
\psi(x,t) = A_0 (x + t)^2
\)
B) \(
\psi(x,t) = A_0 \sin(ax^2 + bt^2)
\)
C) \(
\psi(x,t) = \frac{A_0}{B_0 (x - t)^2 + 1}
\)
D) \(
\psi(x,t) = A_0 e^{(ax + bt)^2}
\)

