Q.No:1 JEST-2012
The Dulong-Petit law fails near room temperature (\(300 K\)) for many light elements (such as boron and beryllium) because their Debye temperature is
(a)
\(\gg 300 K\)
(b)
\(\sim 300 K\)
(c)
\(\ll 300 K\)
(d)
\(0 K\)
Check Answer
Option a
Q.No:2 JEST-2013
Consider a system of two particles A and B. Each particle can occupy one of three possible quantum states \(|1\rangle, |2\rangle\), and \(|3\rangle\). The ratio of the probability that the two particles are in the same state to the probability that the two particles are in different states is calculated for bosons and classical (Maxwell-Boltzman) particles. They are respectively
(a)
\(1, 0\)
(b)
\(1/2, 1\)
(c)
\(1, 1/2\)
(d)
\(0, 1/2\)
Check Answer
Option c
Q.No:3 JEST-2013
Consider three situations of \(4\) particles in a one dimensional box of width \(L\) with hard walls.
(i), the particles are fermions,
In case (ii) they are bosons, and
in case (iii) they are classical.
If the total ground state energy of the four particles in these three cases are \(E_F, E_B\) and \(E_{cl}\) respectively, which of the following is true?
(a)
\(E_F=E_B=E_{cl}\)
(b)
\(E_F>E_B=E_{cl}\)
(c)
\(E_F<E_B<E_{cl}\)
(d)
\(E_F>E_B>E_{cl}\)
Check Answer
Option b
Q.No:4 JEST-2014
An ideal gas of non-relativistic fermions in \(3\)-dimensions is at \(0 K\). When both the number density and mass of the particles are doubled, then the energy per particle is multiplied by a factor
(a)
\(2^{1/2}\)
(b)
\(1\)
(c)
\(2^{1/3}\)
(d)
\(2^{-1/3}\)
Check Answer
Option d
Q.No:5 JEST-2014
What is the contribution of the conduction electrons in the molar entropy of a metal with electronic coefficient of specific heat?
(a)
\(\gamma T\)
(b)
\(\gamma T^2\)
(c)
\(\gamma T^3\)
(d)
\(\gamma T^4\)
Check Answer
Option a
Q.No:6 JEST-2015
For non-interacting Fermions in \(d\)-dimensions, the density of states \(D(E)\) varies as \(E^{\left(\frac{d}{2}-1\right)}\). The Fermi energy \(E_F\) of an \(N\) particle system in \(3\)-, \(2\)- and \(1\)-dimensions will scale respectively as,
(a)
\(N^2, N^{2/3}, N\)
(b)
\(N, N^{2/3}, N^2\)
(c)
\(N, N^{2}, N^{2/3}\)
(d)
\(N^{2/3}, N, N^2\)
Check Answer
Option d
Q.No:7 JEST-2016
Consider \(N\) non-interacting electrons (\(N\sim N_A\)) in a box of sides \(L_x, L_y, L_z\). Assuming that the dispersion relation is \(\epsilon(k)=Ck^4\) where \(C\) is a constant, the ratio of the ground state energy per particle to the Fermi energy is:
(A)
\(3/7\)
(B)
\(7/3\)
(C)
\(3/5\)
(D)
\(5/7\)
Check Answer
Option A
Q.No:8 JEST-2017
A cylinder at temperature \(T=0\) is separated into two compartments A and B by a free sliding piston. Compartments A and B are filled by Fermi gases made of spin \(1/2\) and \(3/2\) particles respectively. If particles in both the compartments have same mass, the ratio of equilibrium density of the gas in compartment A to that of gas in compartment B is
(A)
\(1\).
(B)
\(\frac{1}{3^{2/5}}\).
(C)
\(\frac{1}{2^{2/5}}\).
(D)
\(\frac{1}{2^{2/3}}\).
Check Answer
Option C
Q.No:9 JEST-2017
A system of particles on \(N\) lattice sites is in equilibrium at temperature \(T\) and chemical potential \(\mu\). Multiple occupancy of the sites is forbidden. The binding energy of a particle at each site is \(-\epsilon\). The probability of no site being occupied is
(A)
\(\frac{1-e^{\beta(\mu+\epsilon)}}{1-e^{(N+1)\beta(\mu+\epsilon)}}\).
(B)
\(\frac{1}{[1+e^{\beta(\mu+\epsilon)}]^N}\).
(C)
\(\frac{1}{[1+e^{-\beta(\mu+\epsilon)}]^N}\).
(D)
\(\frac{1-e^{-\beta(\mu+\epsilon)}}{1-e^{-(N+1)\beta(\mu+\epsilon)}}\).
Check Answer
Option B
Q.No:10 JEST-2019
Consider a non-relativistic two-dimensional gas of \(N\) electrons with the Fermi energy \(E_F\). What is the average energy per particle at temperature \(T=0\)?
(A)
\(\frac{3}{5}E_F\)
(B)
\(\frac{2}{5}E_F\)
(C)
\(\frac{1}{2}E_F\)
(D)
\(E_F\)
Check Answer
Option C
Q.No:11 JEST-2019
The energy spectrum of a particle consists of four states with energies \(0, \epsilon, 2\epsilon, 3\epsilon\). Let \(Z_B(T), Z_F(T)\) and \(Z_C(T)\) denote the canonical partition functions for \(\underline{four}\) non-interacting particles at temperature \(T\). The subscripts \(B, F\) and \(C\) corresponds to bosons, fermions and distinguishable classical particles, respectively. Let \(y\equiv \exp{\left(-\frac{\epsilon}{k_B T}\right)}\). Which one of the following statements is true about \(Z_B(T), Z_F(T)\) and \(Z_C(T)\)?
(A)
They are polynomials in \(y\) of degree \(12, 6\) and \(12\), respectively.
(B)
They are polynomials in \(y\) of degree \(16, 10\) and \(16\), respectively.
(C)
They are polynomials in \(y\) of degree \(9, 6\) and \(12\), respectively.
(D)
They are polynomials in \(y\) of degree \(12, 10\) and \(16\), respectively.
Check Answer
Option A
Q.No:12 JEST-2022
The ratio of specific heat of electrons in a heated copper wire at two temperatures \(200^{\circ}C\) and \(100^{\circ}C\) is
(a)
\(1.27\)
(b)
\(2\)
(c)
\(1.41\)
(d)
\(1.61\)
Check Answer
Option a
Q.No:13 JEST-2023
There are three states of energy \(E, 0, -E\) available for the population of two identical non interacting spinless fermions. If they are in equilibrium at temperature T, what is the average energy of the system? The Boltzmann constant is \(k_B\) and consider \(\beta\) to be \(\frac{1}{k_B T}\)
(a) 0
(b) \(\frac{E (e^{\beta E}-e^{-\beta E})}{1+e^{-\beta E}+e^{\beta E}}\)
(c) \(\frac{E (e^{-\beta E}-e^{\beta E})}{1+e^{-\beta E}+e^{\beta E}}\)
(d) \(\frac{E (2e^{-\beta E}+e^{-\beta E}-e^{\beta E}-2 e^{2\beta E})}{2e^{-\beta E}+e^{-\beta E}+2+e^{\beta E}+ e^{2\beta E}}\)
Check Answer
Option c
Q.No:14 JEST-2023
System \(A\) consists of 3 identical non-interacting bosons. System \(B\) consists of 2 identical non-interacting bosons. They both have identical energy spectra-three non-degenerate energy levels \(0, \epsilon, 2\epsilon\). The particles of \(A\) and \(B\) are distributed in various energy levels in such a way that the total energy of the combined system is \(4 \epsilon\). The average energy of the system \(A\) in units of \(\epsilon\) is
(a) \(2.2\)
(b) \(2.3\)
(c) \(2.1\)
(d) \(2.4\)
Check Answer
Option b
Q.No:15 JEST-2024
A system of two noninteracting identical bosons is in thermal equilibrium at temperature \( T \). The particles can be in one of three states with nondegenerate energy eigenvalues \( -\varepsilon \), \( 0 \), and \( \varepsilon \). The temperature \( T \) is such that
\[
\exp\left( -\frac{\varepsilon}{k_B T} \right) = \frac{1}{2}
\]
where \( k_B \) is the Boltzmann's constant. The average energy of the system is found to be \( \langle E \rangle = -\frac{n}{35}\varepsilon \), where \( n \) is an integer. What is the value of \( n \)?
Check Answer
Ans 36
Q.No:16 JEST-2024
The energy spectrum for a system of spinless noninteracting fermions consists of \( (N + 1) \) nondegenerate energy levels \( 0, \varepsilon, 2\varepsilon, \ldots, N\varepsilon \) (\( \varepsilon > 0 \)). Let \( x = \exp \left( -\frac{\varepsilon}{k_B T} \right) \), where \( k_B \) is the Boltzmann constant and \( T \) is the temperature. For \( N \) identical fermions in thermal equilibrium at temperature \( T \), what is the average occupancy of the highest energy level?
(a) \( \frac{x - x^{N+1}}{1 - x^{N+1}} \)
(b) \( \frac{x - x^{N+1}}{1 + x^{N+1}} \)
(c) \( \frac{x}{1 - x^N} \)
(d) \( \frac{x^N}{1 + x^N} \)
Check Answer
option a
Q.No:17 JEST-2024
The density of states of a system of \( N \) particles at energy \( E \) is
\[
g(E, N) =
\begin{cases}
\frac{1}{(\hbar \omega)^N} \frac{E^{N-1}}{(N - 1)!} & \text{for } E \geq 0 \\
0 & \text{for } E < 0
\end{cases}
\]
where \( \hbar \) is the Planck’s constant and \( \omega \) is a natural frequency of the system. Taking \( k_B \) to be the Boltzmann constant, compute the temperature of the system at energy \( E \).
(a) \( \frac{E}{N k_B} \)
(b) \( \frac{1}{k_B} \left( \frac{E}{N} + \frac{1}{2}\hbar \omega \right) \)
(c) \( \frac{1}{k_B} \left( \frac{E}{N} + \hbar \omega \right) \)
(d) \( \frac{1}{k_B} \sqrt{\left( \frac{E}{N} \right)^2 + (\hbar \omega)^2} \)
Check Answer
option a
Q.No:18 JEST-2025
Calculate the partition function for two indistinguishable bosonic particles at a temperature T, which can be distributed in two single-particle energy levels \(\epsilon_{1}\) and \(\epsilon_{2}\). Consider \(\beta = \frac{1}{k_{B}T}\).
a) \(\,e^{-2\beta\epsilon_{1}} + e^{-2\beta\epsilon_{2}} + e^{-2\beta(\epsilon_{1}+\epsilon_{2})}\)
b) \(\frac{1}{2!}\bigl(e^{-\beta\epsilon_{1}} + e^{-\beta\epsilon_{2}}\bigr)^{2}\)
c) \(\bigl(e^{-\beta\epsilon_{1}} + e^{-\beta\epsilon_{2}}\bigr)^{2}\)
d) \(\,e^{-2\beta\epsilon_{1}} + e^{-2\beta\epsilon_{2}} + e^{-\beta(\epsilon_{1}+\epsilon_{2})}\)
Check Answer
option d
Q.No:19 JEST-2025
If the lattice contribution to the \(C_V\) of a solid crystal at temperature \(2\,\text{K}\)
is found to be \(0.5\,\text{mJ mol}^{-1}\text{K}^{-1}\), what will be the corresponding
contribution at temperature \(4\,\text{K}\)?
a) 4 mJ mol⁻¹ K⁻¹
b) 1 mJ mol⁻¹ K⁻¹
c) 8 mJ mol⁻¹ K⁻¹
d) 2 mJ mol⁻¹ K⁻¹
Check Answer
option a
Q.No:20 JEST-2025
The volume of a nucleus, treated as a Fermi gas in three-dimensional space,
is proportional to the number of fermions present in it. If the total number
of fermions is changed from N to 2N, the total energy of the system will
a) be doubled.
b) be half of its original value.
c) be 4 times its original value.
d) remain the same.
Check Answer
option a
Q.No:21 JEST-2025
Consider a two-dimensional Fermi gas at 0 K with Fermi energy \(ε_F\).
The average energy per particle of this gas is:
a) \(3ε_F / 5\)
b) \(ε_F / 3\)
c) \(ε_F / 2\)
d) \(ε_F / 4\)
Check Answer
option c
Q.No:1 TIFR-2014
A gas of photons is enclosed in a container of fixed volume at an absolute temperature \(T\). Noting that the photon is a massless particle (i.e., its energy and momentum are related by \(E=pc\)), the number of photons in the container will vary as
(a)
\(T\)
(b)
\(T^2\)
(c)
\(T^3\)
(d)
\(T^4\)
Check Answer
Option c
Q.No:2 TIFR-2015
Which of the following graphs qualitatively describes the pressure \(P\) of a gas of non-interacting fermions in thermal equilibrium at a constant volume as a function of temperature?

Check Answer
Option a
Q.No:3 TIFR-2015
Bosonic excitations of ferromagnets have a dispersion relation \(\epsilon=\gamma k^2\), where \(\epsilon\) is the energy and \(k\) is the wavevector of the excitation. Assuming a system of such non-interacting bosonic excitations, at low temperature \(T\), the specific heat \(C_V\) of a three-dimensional ferromagnet will be proportional to
(a)
\(T\)
(b)
\(T^{3/2}\)
(c)
\(T^{5/2}\)
(d)
\(T^{3}\)
Check Answer
Option b
Q.No:4 TIFR-2016
The energy per oscillator of an isolated system of a large number of identical non-interacting fermions in a one-dimensional harmonic oscillator potential is \(5\hbar \omega/4\), where \(\omega\) is the angular frequency of the harmonic oscillator. The entropy of the system per oscillator is given by
(a)
\(0.25\)
(b)
\(0.56\)
(c)
\(0.63\)
(d)
\(0.75\)
Check Answer
Option b
Q.No:5 TIFR-2017
In two dimensions, two metals \(A\) and \(B\), have the number density of free electrons in the ratio
\[
n_A:n_B=1:2
\]
The ratio of their Fermi energies is
(a)
\(2:3\)
(b)
\(1:2\)
(c)
\(1:4\)
(d)
\(1:8\)
Check Answer
Option b
Q.No:6 TIFR-2017
The cosmic microwave background radiation in the Universe has a blackbody distribution corresponding to a temperature \(2.735 \hspace{1mm}\text{K}\). In a certain cosmological model, it was assumed that the universe consists purely of radiation and is undergoing adiabatic expansion. In this model it was predicted that the volume of the Universe will be tripled in the next \(10^{10}\) yrs. The corresponding blackbody radiation temperature would be
(a)
\(0.9116 \hspace{1mm}\text{K}\)
(b)
\(2.078 \hspace{1mm}\text{K}\)
(c)
\(1.896 \hspace{1mm}\text{K}\)
(d)
\(1.526 \hspace{1mm}\text{K}\)
Check Answer
Option c
Q.No:7 TIFR-2017
Assume that the crystal structure of metallic copper \(({Cu})\) results in a density of atoms \(\rho_{{Cu}}\)=\(8.46\times 10^{28}\)\(\hspace{1mm}\)\(\text{m}^{-3}\). Each \({Cu}\) atom in the crystal donates one electron to the conduction band, which leads, for the \(3\)-D Fermi gas, to a density of states
\[
g(\varepsilon)=\frac{1}{2\pi^2}\left(\frac{2m^*}{\hbar^2}\right)^{3/2}\varepsilon^{1/2}
\]
where \(m^*\) is the effective mass of the conduction electrons. In the low temperature limit (i.e. \(T=0 \hspace{1mm}\text{K}\)), find the Fermi energy \(E_F\), in units of \(\text{eV}\). You may assume \(m^*\) to be equal to the free electron mass \(m_e\).
Check Answer
Ans 6.87
Q.No:8 TIFR-2018
Consider a monatomic solid lattice at a low temperature \(T\ll T_D\), where \(T_D\) is the characteristic Debye temperature of the solid (\(T_D=\hbar \omega_m/k_B\) where \(\omega_m\) is the maximum possible frequency of the lattice vibrations). The heat capacity of the solid is proportional to
(a)
\(T/T_D\)
(b)
\((T/T_D)^3\)
(c)
\(T_D/T\)
(d)
\((T_D/T)^2\)
Check Answer
Option b
Q.No:9 TIFR-2019
Consider a thermal ensemble at temperature \(T\) which is composed of identical quantum harmonic oscillators of frequency \(\omega_0\) with non-overlapping wavefunctions. The probability that there will be an even number of energy quanta in the system is
(a)
\(\frac{1}{\exp{(-\hbar \omega_0/k_B T)}+1}\)
(b)
\(\frac{1}{\exp{(\hbar \omega_0/k_B T)}+1}\)
(c)
\((\frac{1}{\exp{(-\hbar \omega_0/k_B T)}-1}\)
(d)
\(\tanh{(\hbar \omega_0/2k_B T)}\)
Check Answer
Option a
Q.No:10 TIFR-2019
An ideal monatomic gas at chemical potential \(\mu=-1 \hspace{1mm}\text{eV}\) and a temperature given by \(k_B T=0.1 \hspace{1mm} \text{eV}\) is in equilibrium with an adsorbing metal surface, i.e. there are isolated sites distributed randomly on the metal surface where the gas atom can get bound. Each such binding site can adsorb \(0, 1\), or \(2\) atoms with the released energy being \(0, -1 \hspace{1mm} \text{eV}\) and \(-1.9 \hspace{1mm}\text{eV}\) respectively. The average number of adsorbed molecules at each site would be
(a)
\(\frac{1+e}{1-e}\)
(b)
\(\frac{1+e}{1+2e}\)
(c)
\(\frac{2+e}{1+2e}\)
(d)
\(\frac{1+2e}{1+e}\)
Check Answer
Option c
Q.No:11 TIFR-2019
At low temperatures, the measured specific heat \(C_V\) of a solid sample is found to depend on temperature as
\[
C_V=aT^{3/2}+bT^3.
\]
where \(a\) and \(b\) are constants. This material has
(a)
one fermionic excitation with dispersion relation \(\omega\propto k^4\); another bosonic excitation with dispersion relation \(\omega\propto k\)
(b)
one fermionic excitation with dispersion relation \(\omega\propto k^2\); another bosonic excitation with dispersion relation \(\omega\propto k^4\)
(c)
one bosonic excitation with dispersion relation \(\omega\propto k^2\); another bosonic excitation with dispersion relation \(\omega\propto k\)
(d)
one fermionic excitation with dispersion relation \(\omega\propto k^2\); another fermionic excitation with dispersion relation \(\omega\propto k\)
Check Answer
Option c
Q.No:12 TIFR-2021
In a Universe with only two spatial dimensions, the total energy radiated by a perfect blackbody across all wavelengths per unit surface area per unit time is proportional to
(a)
\(T^3\)
(b)
\(T^4\)
(c)
\(T^2\)
(d)
\(T^{3/2}\)
Check Answer
Option a
Q.No:13 TIFR-2021
The temperature dependence of specific heat of two metals A and B, both with quadratic dispersion relations are shown in the figure below.
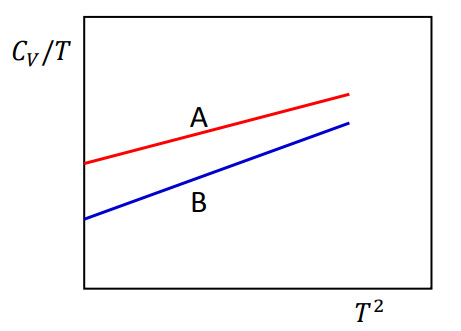
Which of the following statements is necessarily false?
(a)
The density of states at Fermi energy of A is smaller than that of B.
(b)
The effective mass of B is larger than that of A.
(c)
The effective mass of A is smaller than that of B.
(d)
The density of states at Fermi energy of B is smaller than that of A.
Check Answer
Option a
Q.No:14 TIFR-2022
A particle of mass \(m\) in a three-dimensional potential well has a Hamiltonian of the form
\[H=\frac{p_x^2}{2m}+\frac{p_y^2}{2m}+\frac{p_z^2}{2m}+\frac{1}{2} m \omega^2 x^2+\frac{1}{2} m \omega^2 y^2+2 m \omega^2 z^2\]
where \(\omega\) is a constant. If there are two identical spin-\(\frac{1}{2}\) particles in this potential having a total energy
\[E=6\hbar \omega\]
the entropy of the system will be
(a)
\(k_B \hspace{1mm} ln \hspace{1mm} 14 \)
(b)
\(k_B \hspace{1mm} ln \hspace{1mm} 16 \)
(c)
\(k_B \hspace{1mm} ln \hspace{1mm} 12 \)
(d)
\(k_B \hspace{1mm} ln \hspace{1mm} 10 \)
Check Answer
Option a
Q.No:15 TIFR-2022
A quantum dot is constructed such that it has just three energy levels, with energies \(E\),\(2E\) and \(3E\) respectively. The chemical potential in the system has the value \(\mu=2E\) and the temperature is given by
\[T= \frac{E}{2k_B}\]
The expected number of electrons populating the quantum dot will be
(a)
3.0
(b)
2.5
(c)
1.5
(d)
4.0
Check Answer
Option a
Q.No:16 TIFR-2022
The low-temperature specific heat of a certain material is primarily due to acoustic phonons. The frequency \(\omega\) of a phonon is related to its wavevector \(k\) by \(\omega=ck\), where \(c\) is the speed of sound in the material. The phonons have a Bose distribution
\[n(k)=\frac{1}{e^{\hbar c k /k_B T}-1}\]
and the energy of a phonon has a maximum possible value \(\omega_D\).
In a two-dimensional sample, the specific heat at low-temperatures behaves as
(a)
\((\frac{T}{\omega_D})^2\)
(b)
\((\frac{T}{\omega_D})^3\)
(c)
\((\frac{T}{\omega_D})^{3/2}\)
(d)
\(\frac{T}{\omega_D}\)
Check Answer
Option a
Q.No:17 TIFR-2022
A pseudo-potential \(V_{12}\) between every pair of particles in an ideal gas is to be constructed which will reproduce the effects of quantum statistics if the gas particles are bosonic in nature. A correct formula for this, in terms of the inter-particle distance \(r_{12}\) and a mean distance \(\lambda\), will be of the form
(a)
\(V_{12}=-k_B T \hspace{0.3mm} ln \hspace{0.3mm} (1+e^{-2\pi r_{12}^2 /\lambda^2})\)
(b)
\(V_{12}=-k_B T \hspace{0.3mm} ln \hspace{0.3mm} (1-e^{-2\pi r_{12}^2 /\lambda^2})\)
(c)
\(V_{12}=+k_B T \hspace{0.3mm} ln \hspace{0.3mm} (1+e^{-2\pi r_{12}^2 /\lambda^2})\)
(d)
\(V_{12}=+k_B T \hspace{0.3mm} ln \hspace{0.3mm} (1-e^{-2\pi r_{12}^2 /\lambda^2})\)
Check Answer
Option a
Q.No:18 TIFR-2023
Five identical bosons are distributed in energy levels \(E_1\) and \(E_2\) with degeneracy of 2 and 3 respectively. Find the number of microstates if there are three bosons in the energy level \(E_1\) and two bosons in the energy level \(E_2\).
(a)
24
(b)
6
(c)
1024
(d)
120
Check Answer
Option a
Q.No:19 TIFR-2023
Consider a fermionic system with a Hamiltonian
\[\hat{H}=\begin{vmatrix}0&E_0&0\\E_0&0&2E_0 \\ 0&2E_0&0\end{vmatrix}\]
Consider the grand canonical ensemble of this system at temperature \(T\) and zero chemical potential, where \(k_B\) is the Boltzmann constant. The grand canonical partition function of the system is given by
(a)
\(cos \hspace{0.3mm}h(\sqrt{5}\frac{E_0}{k_B T})\)
(b)
\(\frac{1}{4+cos \hspace{0.3mm}h(\sqrt{5}\frac{E_0}{k_B T}) }\)
(c)
\(sec \hspace{0.3mm}h(\sqrt{5}\frac{E_0}{k_B T})\)
(d)
\(4+cos \hspace{0.3mm}h(\sqrt{5}\frac{E_0}{k_B T})\)
Check Answer
Option d
Q.No:20 TIFR-2024
Each site of a linear chain of \( N \) sites has a spin which can be in three different states with energies \( 0, \pm \epsilon \), as shown in the figure below.

The system has a constraint that the neighbouring spins cannot be in the same state. At infinite temperature, the entropy of the system is given by:
(a) \( N \ln 2 + \ln \frac{3}{2} \)
(b) \( N \ln 3 \)
(c) \( (N - 1) \ln 2 \)
(d) \( N \ln 2 \)
Check Answer
Option a
Q.No:21 TIFR-2024
The energy dispersion in the conduction band of a one-dimensional metal with lattice spacing \( a \) is given by,
\[
E(k) = E_0(1 - \cos ka)
\]
where \( k \in [-\pi/a, +\pi/a] \). Suppose that each site contributes one conduction electron to the conduction band. What is the Fermi energy of the system?
(a) \( E_0 \)
(b) \( \frac{E_0}{2} \)
(c) \( 2E_0 \)
(d) \( \frac{E_0}{4} \)
Check Answer
Option a
Q.No:22 TIFR-2025
Consider a two-dimensional insulating solid crystal.
At low temperature, how does the specific heat at constant area
\(c_{a} = \frac{d\epsilon}{dT}\), where \(\epsilon\) is the energy per unit area,
depend on \(T\)?
a) \(c_{a} \sim T^{2}\)
b) \(c_{a} \sim T^{3}\)
c) \(c_{a} \sim T\)
d) \(c_{a}\ \text{is independent of}\ T\)
Check Answer
Option a
Q.No:23 TIFR-2025
Two types of particles \(A\) and \(B\) have the same mass,
but are distinguished by an internal degree of freedom.
A classical ideal gas in a volume \(V\) at temperature \(T\) contains:
Case (X): \(2N\) particles of A-type
Case (Y): \(N\) particles of A-type and \(N\) particles of B-type
Which of the following is true?
a) Pressure of (X) and (Y) are same; (Y) has more entropy than (X)
b) Pressure of (X) and (Y) are same; (X) has more entropy than (Y)
c) Pressure of (X) is greater than pressure of (Y); (X) has more entropy than (Y)
d) Pressure of (X) is greater than pressure of (Y); (Y) has more entropy than (X)
Check Answer
Option a
Q.No:24 TIFR-2025
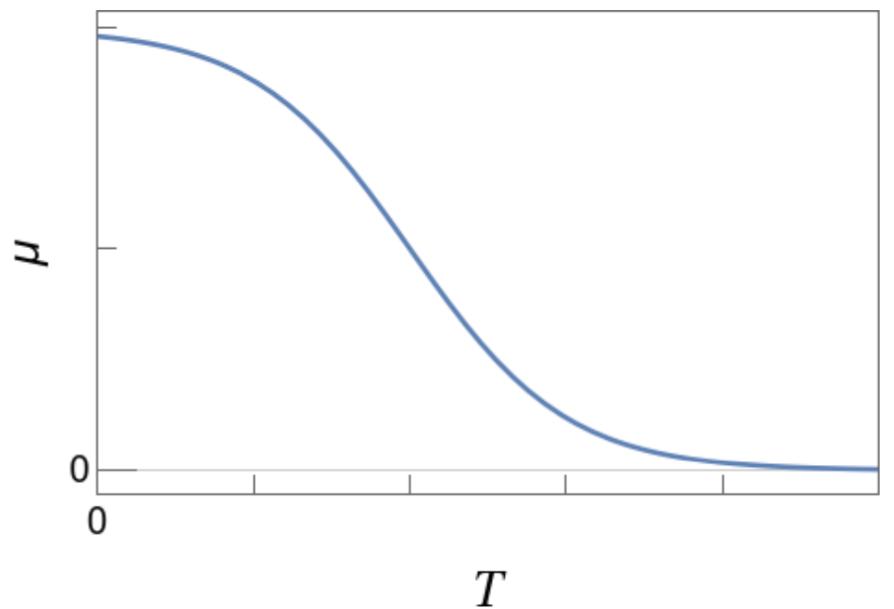
Consider a (non-relativistic) gas of fermions in a container with a fixed density \(n\).
Which plot best describes how the chemical potential \(\mu\) changes with temperature \(T\)?
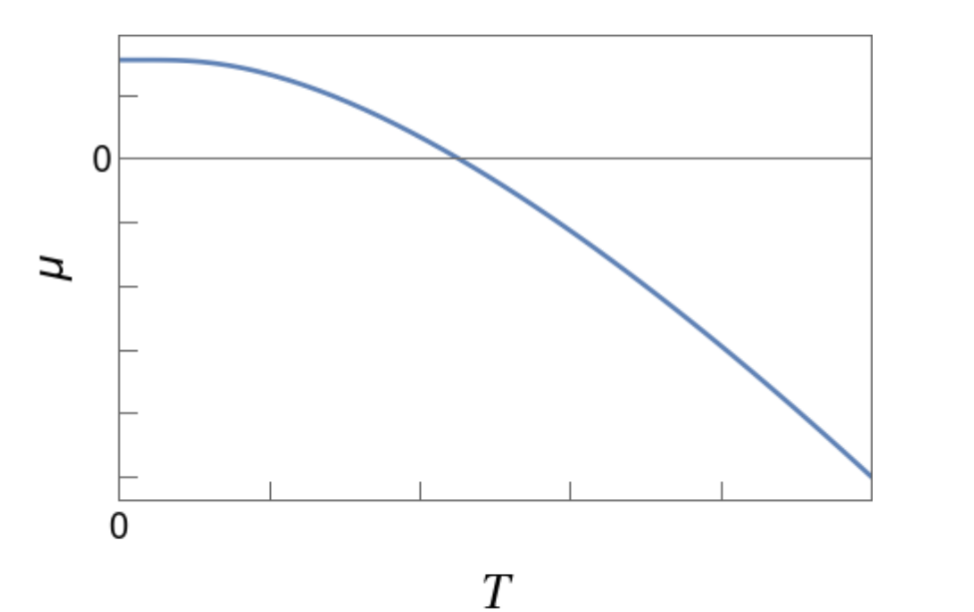
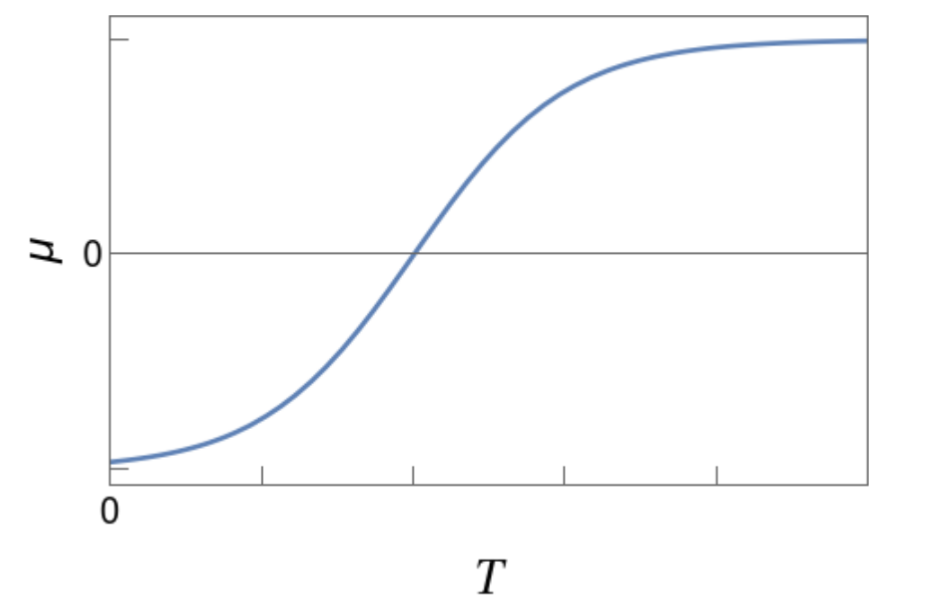
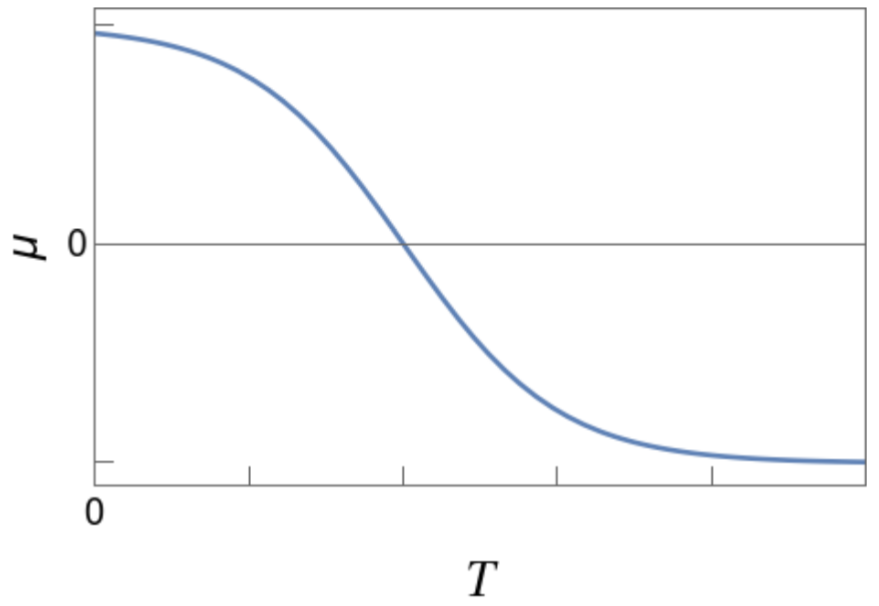

Q.No.1 Discussion (JEST) :
Q.No.2 Discussion (JEST) :
Pendulum in elevator problem
Q.No.3 Discussion (JEST) :
Option B
Q.No.4 Discussion (JEST):
Q.No.5 Discussion (JEST) :
Concept -electronic specific heat
Q.No.6 Discussion (JEST) :
Answer
Q.No.7 Discussion (JEST) :
Option A
Q.No.8 Discussion (JEST) :
Q.No.9 Discussion (JEST) :
Q.9. JEST
Q.No.10 Discussion (JEST) :
Answer: C
Q.No.11 Discussion (JEST) :
Q.No.12 Discussion (JEST) :
Q.No.13 Discussion (JEST) :
Q.No.14 Discussion (JEST) :
Q.No.1 Discussion (TIFR) :
Q.No.2 Discussion (TIFR) :
Q.No.3 Discussion (TIFR) :
Q.No.4 Discussion (TIFR) :
Q.No.5 Discussion (TIFR) :
Q.No.6 Discussion (TIFR) :
Q.No.7 Discussion (TIFR) :
Q.No.8 Discussion (TIFR) :
Q.No.9 Discussion (TIFR) :
Q.No.10 Discussion (TIFR) :
Q.No.11 Discussion (TIFR) :
Q.No.12 Discussion (TIFR) :
Q.No.13 Discussion (TIFR) :
Q.No.14 Discussion (TIFR) :
Q.No.15 Discussion (TIFR) :
Q.No.16 Discussion (TIFR) :
Q.No.17 Discussion (TIFR) :
Q.No.18 Discussion (TIFR) :
Q.No.19 Discussion (TIFR) :
Q.No.20 Discussion (TIFR) :