Q.No:1 GATE-2012
A rod of proper length \(l_0\) oriented parallel to the \(x\)-axis moves with speed \(2c/3\) along the \(x\)-axis in the \(S\)-frame, where \(c\) is the speed of the light in free space. The observer is also moving along the \(x\)-axis with speed \(c/2\) with respect to the \(S\)-frame. The length of the rod as measured by the observer is
(A)
\(0.35l_0\)
(B)
\(0.48l_0\)
(C)
\(0.87l_0\)
(D)
\(0.97l_0\)
Check Answer
Option D
Q.No:2 GATE-2013
An electron is moving with a velocity of \(0.85c\) in the same direction as that of a moving photon. The relative velocity of the electron with respect to photon is
(A)
\(c\)
(B)
\(-c\)
(C)
\(0.15c\)
(D)
\(-0.15c\)
Check Answer
Option B
Q.No:3 GATE-2013
The relativistic form of Newton's second law of motion is
(A)
\(F=\frac{mc}{\sqrt{c^2-v^2}} \frac{dv}{dt}\)
(B)
\(F=\frac{m\sqrt{c^2-v^2}}{c} \frac{dv}{dt}\)
(C)
\(F=\frac{mc^2}{c^2-v^2} \frac{dv}{dt}\)
(D)
\(F=m\frac{c^2-v^2}{c^2} \frac{dv}{dt}\)
Check Answer
Option C
Q.No:4 GATE-2014
If the half-life of an elementary particle moving with speed \(0.9c\) in the laboratory frame is \(5\times 10^{-8} s\), then the proper half-life is _____________\(\times 10^{-8} s\). (\(c=3\times 10^8 m/s\))
Check Answer
Ans 2.1-2.3
Q.No:5 GATE-2015
In an inertial frame \(S\), two events \(A\) and \(B\) take place at (\(ct_A=0, \vec{r}_A=0\)) and (\(ct_B=0, \vec{r}_B=2\hat{y}\)), respectively. The times at which these events take place in a frame \(S'\) moving with a velocity \(0.6c\hat{y}\) with respect to \(S\) are given by
(A)
\(ct'_A=0; ct'_B=-3/2\)
(B)
\(ct'_A=0; ct'_B=0\)
(C)
\(ct'_A=0; ct'_B=3/2\)
(D)
\(ct'_A=0; ct'_B=1/2\)
Check Answer
Option A
Q.No:6 GATE-2016
The kinetic energy of a particle of rest mass \(m_0\) is equal to its rest mass energy. Its momentum in units of \(m_0 c\), where \(c\) is the speed of light in vacuum, is ___________. (Give your answer upto two decimal places)
Check Answer
Ans 1.72-1.74
Q.No:7 GATE-2016
In an inertial frame of reference \(S\), an observer finds two events occurring at the same time at coordinates \(x_1=0\) and \(x_2=d\). A different inertial frame \(S'\) moves with velocity \(v\) with respect to \(S\) along the positive \(x\)-axis. An observer in \(S'\) also notices these two events and finds them to occur at times \(t_1'\) and \(t_2'\) and at positions \(x_1'\) and \(x_2'\), respectively. If \(\Delta t'=t_2'-t_1', \Delta x'=x_2'-x_1'\) and \(\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\), which of the following statements is true?
(A)
\(\Delta t'=0, \Delta x'=\gamma d\)
(B)
\(\Delta t'=0, \Delta x'=d/\gamma\)
(C)
\(\Delta t'=-\gamma vd/c^2, \Delta x'=\gamma d\)
(D)
\(\Delta t'=-\gamma vd/c^2, \Delta x'=d/\gamma\)
Check Answer
Option C
Q.No:8 GATE-2017
An object travels along the \(x\)-direction with velocity \(c/2\) in a frame \(O\). An observer in a frame \(O'\) sees the same object travelling with velocity \(c/4\). The relative velocity of \(O'\) with respect to \(O\) in units of \(c\) is __________. (up to two decimal places).
Check Answer
Ans 0.27-0.31
Q.No:9 GATE-2018
A spaceship is travelling with a velocity of \(0.7c\) away from a space station. The spaceship ejects a probe with a velocity \(0.59c\) opposite to its own velocity. A person in the space station would see the probe moving at a speed \(Xc\), where the value of \(X\) is ______________ (up to three decimal places).
Check Answer
Ans 0.185-0.189
Q.No:10 GATE-2019
Two spaceships A and B, each of the same rest length \(L\), are moving in the same direction with speeds \(\frac{4c}{5}\) and \(\frac{3c}{5}\), respectively, where \(c\) is the speed of light. As measured by B, the time taken by A to completely overtake B [see figure below] in units of \(L/c\) (to the nearest integer) is _____________

Check Answer
Ans 5
Q.No:11 GATE-2019
Two events, one on the earth and the other one on the Sun, occur simultaneously in the earth's frame. The time difference between the two events as seen by an observer in a spaceship moving with velocity \(0.5c\) in the earth's frame along the line joining the earth to the Sun is \(\Delta t\), where \(c\) is the speed of light. Given that light travels from the Sun to the earth in \(8.3\) minutes in the earth's frame, the value of \(|\Delta t|\) in minutes (rounded off to two decimal places) is _______________-.
Check Answer
Ans 4.77-4.81
Q.No:12 GATE-2021
Two observers \(O\) and \(O'\) observe two events \(P\) and \(Q\). The observers have a constant relative speed of \(0.5c\). In the units, where the speed of light, \(c\), is taken as unity, the observer \(O\) obtained the following coordinates:
Event \(P\): \(x=5, y=3, z=5, t=3\)
Event \(Q\): \(x=5, y=1, z=3, t=5\)
The length of the space-time interval between these two events, as measured by \(O'\), is \(L\). The value of \(|L|\) (in integer) is ____________________.
Check Answer
Ans 2
Q.No:13 GATE-2022
Two identical particles of rest mass \(m_0\) approach each other with equal and opposite velocity \(v=0.5c\), where \(c\) is the speed of light. The total energy of one particle as measured in the rest frame of the other is \(E=\alpha m_0 c^2\). The value of \(\alpha\) is ------------------- (Round off to two decimal places)
Check Answer
Ans 1.65-1.70
Q.No:14 GATE-2023
A rod \(PQ\) of proper length \(L\) lies along the x-axis and moves towards the positive \(x\) direction with speed \(v=\frac{3c}{5}\)
with respect to the ground (see figure), where \(c\) is the speed of light in vacuum. An observer on the ground measures the positions of \(P\) and \(Q\) at different times \(t_P\) and \(t_Q\) respectively in the ground frame, and finds the difference between them to be \(\frac{9L}{10}\). What is the value of \(t_P-t_Q\)?
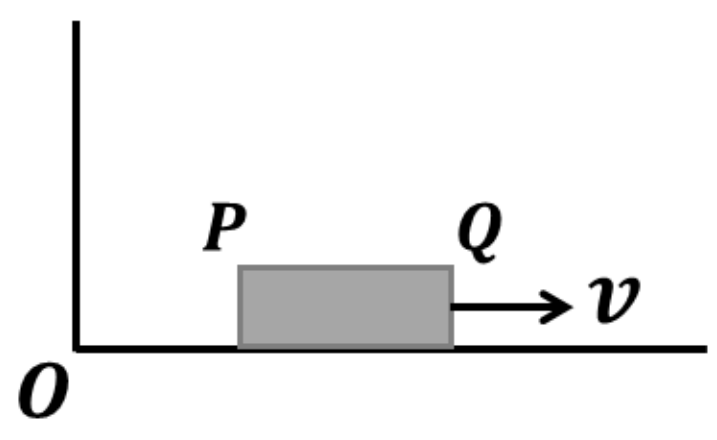
(A)
\(\frac{L}{3c}\)
(B)
\(\frac{L}{5c}\)
(C)
\(\frac{L}{6c}\)
(D)
\(\frac{2L}{3c}\)
Check Answer
Option C
Q.No:15 GATE-2024
An inertial observer sees two spacecrafts \( S \) and \( T \) flying away from each other along the x-axis with individual speed \( 0.5c \), where \( c \) is the speed of light. The speed of \( T \) with respect to \( S \) is
A) \( \frac{4}{5}c \)
B) \( \frac{4}{3}c \)
C) \( c \)
D) \( \frac{2}{3}c \)
Check Answer
Option C
Q.No:16 GATE-2024
An inertial observer sees two spacecrafts \( S \) and \( T \) flying away from each other along the x-axis with individual speed \( 0.5c \), where \( c \) is the speed of light. The speed of \( T \) with respect to \( S \) is
A) \( \frac{4}{5}c \)
B) \( \frac{4}{3}c \)
C) \( c \)
D) \( \frac{2}{3}c \)
Check Answer
Option A
Q.No:17 GATE-2025
Which of the following option(s) is/are correct for photons?
A) Its rest mass is zero, but its energy is non-zero
B) It carries non-zero linear momentum
C) It carries zero spin angular momentum
D) It has two linearly independent states of polarization
Check Answer
Option A,B,D
Q.No:18 GATE-2025
In coordinates \( (t,x) \), a contravariant second-rank tensor \( A \) has non-zero diagonal
components \( A^{tt} = P \) and \( A^{xx} = Q \), with all other components vanishing.
Here \( t \) is the time coordinate and \( x \) is the space coordinate.
Consider a Lorentz transformation \( (t,x) \rightarrow (t',x') \) to a frame moving
with relative speed \( v \) in the \( +x \) direction, so that \( A \rightarrow A' \).
If \( A'^{tt} \) and \( A'^{xx} \) are the diagonal components of \( A' \), then,
setting the speed of light \( c = 1 \) and with
\( \gamma = \frac{1}{\sqrt{1 - v^2}} \),
which of the following option(s) is/are correct?
A) \( A'^{tt} = \gamma^{2} P + \gamma^{2} v^{2} Q \)
B) \( A'^{tt} = \gamma^{2} v^{2} P + v^{2} Q \)
C) \( A'^{xx} = \gamma^{2} v^{2} P + \gamma^{2} Q \)
D) \( A'^{xx} = v^{2} P + \gamma^{2} Q \)
Check Answer
Option A,C
Q.No:19 GATE-2025
The energy of a free, relativistic particle of rest mass \( m \) moving along the \( x \)-axis
in one dimension is denoted by \( T \). When moving in a given potential \( V(x) \),
its Hamiltonian is \( H = T + V(x) \).
In the presence of this potential, its speed is \( v \), conjugate momentum is \( p \),
and the Lagrangian is \( L \). Which of the following option(s) is/are correct?
A) \( H = c^{2}\sqrt{m^{2} + \frac{p^{2}}{c^{2}}} + V(x) \)
B) \( v = \frac{pc}{\sqrt{p^{2} + m^{2}c^{2}}} \)
C) \( L = mc^{2}\sqrt{1 - \frac{v^{2}}{c^{2}}} - V(x) \)
D) \( L = -mc^{2}\sqrt{1 - \frac{v^{2}}{c^{2}}} - V(x) \)
Check Answer
Option A,B,D
Q.No:1 CSIR Dec-2014
According to the special theory of relativity, the speed \(v\) of a free particle of mass \(m\) and total energy \(E\) is:
(1)
\(v=c\sqrt{1-\frac{mc^2}{E}}\)
(2)
\(v=\sqrt{\frac{2E}{m}}\left(1+\frac{mc^2}{E}\right)\)
(3)
\(v=c\sqrt{1-\left(\frac{mc^2}{E}\right)^2}\)
(4)
\(v=c\left(1+\frac{mc^2}{E}\right)\)
Check Answer
Option 3
Q.No:2 CSIR June-2015
Consider three inertial frames of reference
A. B and C. The frame B moves with a vclocity \(c/2\) with respect to A, and C moves with a velocity \(c/10\) with respect to B in the same direction. The velocity of C as measured in A is
(1)
\(\frac{3c}{7}\)
(2)
\(\frac{4c}{7}\)
(3)
\(\frac{c}{7}\)
(4)
\(\frac{\sqrt{3c}}{7}\)
Check Answer
Option 2
Q.No:3 CSIR June-2015
A rod of length \(L\) carries a total charge \(Q\)
distributed uniformly. If this is observed in a frame moving with a speed \(v\) along the rod, the charge per unit length (as measured by the moving observer) is
(1)
\(\frac{Q}{L}\left(1-\frac{v^{2}}{c^{2}}\right)\)
(2)
\(\frac{Q}{L} \sqrt{1-\frac{v^{2}}{c^{2}}}\)
(3)
\(\frac{Q}{L \sqrt{1-\frac{v^{2}}{c^{2}}}}\)
(4)
\(\frac{Q}{L\left(1-\frac{v^{2}}{c^{2}}\right)}\)
Check Answer
Option 3
Q.No:4 CSIR Dec-2015
Consider a particle of mass \(m\) moving with a speed \(v\). If \(T_R\) denotes the relativistic kinetic energy and \(T_N\) its non-relativistic approximation, then the value of \((T_R-T_N)/T_R\) for \(v=0.01 c\), is
(1)
\(1.25\times 10^{-5}\)
(2)
\(5.0\times 10^{-5}\)
(3)
\(7.5\times 10^{-5}\)
(4)
\(1.0\times 10^{-4}\)
Check Answer
Option 3
Q.No:5 CSIR Dec-2015
A distant source, emitting radiation of frequency \(\omega\), moves with a velocity \(4c/5\) in a certain direction with respect to a receiver (as shown in the figure).
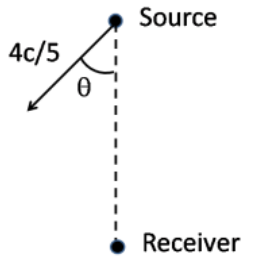
The upper cut-off frequency of the receiver is \(3\omega/2\). Let \(\theta\) be the angle as shown. For the receiver to detect the radiation, \(\theta\) should at least be
(1)
\(\cos^{-1}{\left(\frac{1}{2}\right)}\)
(2)
\(\cos^{-1}{\left(\frac{3}{4}\right)}\)
(3)
\(\cos^{-1}{\left(\frac{2}{\sqrt{5}}\right)}\)
(4)
\(\cos^{-1}{\left(\sqrt{\frac{2}{3}}\right)}\)
Check Answer
Option 2
Q.No:6 CSIR June-2016
Let \((x, t)\) and \((x', t')\) be the coordinate systems used by the observers \(O\) and \(O'\), respectively. Observer \(O'\) moves with a velocity \(v=\beta c\) along their common positive \(x\)-axis. If \(x_+=x+ct\) and \(x_-=x-ct\) are the linear combinations of the coordinates, the Lorentz transformation relating \(O\) and \(O'\) takes the form
(1)
\(x_+'=\frac{x_--\beta x_+}{\sqrt{1-\beta^2}}\) and \(x_-'=\frac{x_+-\beta x_-}{\sqrt{1-\beta^2}}\),
(2)
\(x_+'=\sqrt{\frac{1+\beta}{1-\beta}}x_+\) and \(x_-'=\sqrt{\frac{1-\beta}{1+\beta}}x_-\),
(3)
\(x_+'=\frac{x_+-\beta x_-}{\sqrt{1-\beta^2}}\) and \(x_-'=\frac{x_--\beta x_+}{\sqrt{1-\beta^2}}\),
(4)
\(x_+'=\sqrt{\frac{1-\beta}{1+\beta}}x_+\) and \(x_-'=\sqrt{\frac{1+\beta}{1-\beta}}x_-\),
Check Answer
Option 4
Q.No:7 CSIR June-2016
For a particle of energy \(E\) and momentum \(\mathbf{p}\) (in a frame \(F\)), the rapidity \(y\) is defined as \(y=\frac{1}{2}\ln{\left(\frac{E+p_3 c}{E-p_3 c}\right)}\). In a frame \(F'\) moving with velocity \(\mathbf{v}=(0, 0, \beta c)\) with respect to \(F\), the rapidity \(y'\) will be
(1)
\(y'=y+\frac{1}{2}\ln{(1-\beta^2)}\)
(2)
\(y'=y-\frac{1}{2}\ln{\left(\frac{1+\beta}{1-\beta}\right)}\)
(3)
\(y'=y+\ln{\left(\frac{1+\beta}{1-\beta}\right)}\)
(4)
\(y'=y+2\ln{\left(\frac{1+\beta}{1-\beta}\right)}\)
Check Answer
Option 2
Q.No:8 CSIR Dec-2016
A relativistic particle moves with a constant velocity \(v\) with respect to the laboratory frame. In time \(\tau\), measured in the rest frame of the particle, the distance that it travels in the laboratory frame is
(1)
\(v\tau\)
(2)
\(\frac{c\tau}{\sqrt{1-\frac{v^2}{c^2}}}\)
(3)
\(v\tau\sqrt{1-\frac{v^2}{c^2}}\)
(4)
\(\frac{v\tau}{\sqrt{1-\frac{v^2}{c^2}}}\)
Check Answer
Option 4
Q.No:9 CSIR Dec-2016
Consider a radioactive nucleus that is travelling at a speed \(c/2\) with respect to the lab frame. It emits \(\gamma\)-rays of frequency \(\nu_0\) in its rest frame. There is a stationary detector (which is not on the path of the nucleus) in the lab. If a \(\gamma\)-ray photon is emitted when the nucleus is closest to the detector, its observed frequency at the detector is
(1)
\(\frac{\sqrt{3}}{2}\nu_0\)
(2)
\(\frac{1}{\sqrt{3}}\nu_0\)
(3)
\(\frac{1}{\sqrt{2}}\nu_0\)
(4)
\(\sqrt{\frac{2}{3}}\nu_0\)
Check Answer
Option 1
Q.No:10 CSIR June-2017
An inertial observer sees two events \(E_1\) and \(E_2\) happening at the same location but \(6 \mu s\) apart in time. Another observer moving with a constant velocity \(v\) (with respect to the first one) sees the same events to be \(9 \mu s\) apart. The spatial distance between the events, as measured by the second observer, is approximately
(1)
\(300 m\)
(2)
\(1000 m\)
(3)
\(2000 m\)
(4)
\(2700 m\)
Check Answer
Option 3
Q.No:11 CSIR Dec-2017
A light signal travels from a point A to a point B, both within a glass slab that is moving with uniform velocity (in the same direction as the light) with speed \(0.3c\) with respect to an external observer. If the refractive index of the slab is \(1.5\), then the observer will measure the speed of the signal as
(1)
\(0.67c\)
(2)
\(0.81c\)
(3)
\(0.97c\)
(4)
\(c\)
Check Answer
Option 2
Q.No:12 CSIR Dec-2017
In an inertial frame \(\mathbf{S}\), the magnetic vector potential in a region of space is given by \(\vec{A}=az\hat{i}\) (where \(a\) is a constant) and the scalar potential is zero. The electric and magnetic fields seen by an inertial observer moving with a velocity \(v\hat{i}\) with respect to \(\mathbf{S}\), are, respectively [In the following \(\gamma=\frac{1}{\sqrt{1-v^2/c^2}}\).]
(1)
\(0\) and \(\gamma a\hat{j}\)
(2)
\(-va\hat{k}\) and \(\gamma a\hat{i}\)
(3)
\(v\gamma a\hat{k}\) and \(v\gamma a\hat{j}\)
(4)
\(v\gamma a\hat{k}\) and \(\gamma a\hat{j}\)
Check Answer
Option 4
Q.No:13 CSIR June-2018
Two particles \(A\) and \(B\) move with relativistic velocities of equal magnitude \(v\), but in opposite directions, along the \(x\)-axis of an inertial frame of reference. The magnitude of the velocity of \(A\), as seen from the rest frame of \(B\), is
(1)
\(2v/\left(1-\frac{v^2}{c^2}\right)\)
(2)
\(2v/\left(1+\frac{v^2}{c^2}\right)\)
(3)
\(2v\sqrt{\frac{c-v}{c+v}}\)
(4)
\(2v/\sqrt{1-\frac{v^2}{c^2}}\)
Check Answer
Option 2
Q.No:14 CSIR June-2018
An inertial frame \(K'\) moves with a constant speed \(v\) with respect to another inertial frame \(K\) along their common \(x\)-axis in the positive \(x\)-direction. Let \((x, ct)\) and \((x', ct')\) denote the space-time coordinates in the frames \(K\) and \(K'\), respectively. Which of the following space-time diagrams correctly describes the \(t'\)-axis (\(x'=0\) line) and the \(x'\)-axis (\(t'=0\) line) in the \(x\)-\(ct\) plane? (In the following figures \(\tan{\varphi}=v/c\).)
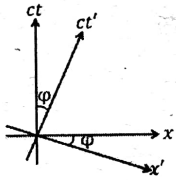

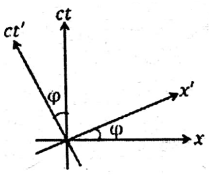

Check Answer
Option 2
Q.No:15 CSIR June-2018
The energy of a free relativistic particle is \(E=\sqrt{|\vec{p}|^2 c^2+m^2 c^4}\), where \(m\) is its rest mass, \(\vec{p}\) is its momentum and \(c\) is the speed of light in vacuum. The ratio \(v_g/v_p\) of the group velocity \(v_g\) of a quantum mechanical wave packet (describing this particle) to the phase velocity \(v_p\) is
(1)
\(|\vec{p}| c/E\)
(2)
\(|\vec{p}|mc^3/E^2\)
(3)
\(|\vec{p}|^2 c^2/E^2\)
(4)
\(|\vec{p}| c/2E\)
Check Answer
Option 3
Q.No:16 CSIR Dec-2018
A relativistic particle of mass \(m\) and charge \(e\) is moving in a uniform electric field of strength \(\mathcal{E}\). Starting from rest at \(t=0\), how much time will it take to reach the speed \(c/2\)?
(1)
\(\frac{1}{\sqrt{3}} \frac{mc}{e\mathcal{E}}\)
(2)
\(\frac{mc}{e\mathcal{E}}\)
(3)
\(\sqrt{2} \frac{mc}{e\mathcal{E}}\)
(4)
\(\sqrt{\frac{3}{2}} \frac{mc}{e\mathcal{E}}\)
Check Answer
Option 1
Q.No:17 CSIR June-2019
A point charge is moving with a uniform velocity \(\beta c\) along the positive \(x\)-direction, parallel to and very close to a corrugated metal sheet (see the figure below).

The wavelength of the electromagnetic radiation received by an observer along the direction of motion is
(1)
\(\frac{L}{\beta}\sqrt{1-\beta^2}\)
(2)
\(L\sqrt{1-\beta^2}\)
(3)
\(L\beta \sqrt{1-\beta^2}\)
(4)
\(L\)
Check Answer
Option 1
Q.No:18 Assam CSIR Dec-2019
Two particles, each of rest mass \(M\) and speed \(0.8c\) are moving towards each other in an inertial frame. They collide to form a single particle. The rest mass of the new particle is
(1)
\(\frac{4}{3}M\)
(2)
\(\frac{10}{3}M\)
(3)
\(\frac{5}{3}M\)
(4)
\(2M\)
Check Answer
Option 2
Q.No:19 Assam CSIR Dec-2019
Light emitted at \((ct, x, y, z)\) is absorbed at \((c(t+\Delta t), x+\Delta x, y+\Delta y, z+\Delta z)\) when propagating in a medium with refractive index \(n\). The square of the proper time between the two events is
(1)
\(\left(\frac{n^2-1}{n^2+1}\right)(\Delta t)^2\)
(2)
\(\left(\frac{n^2}{n^2+1}\right)(\Delta t)^2\)
(3)
\(\left(\frac{n^2-1}{n^2}\right)(\Delta t)^2\)
(4)
\(\left(\frac{n-1}{n+1}\right)(\Delta t)^2\)
Check Answer
Option 3
Q.No:20 CSIR June-2020
A heavy particle of rest mass \(M\) while moving along the positive \(z\)-direction, decays into two identical light particles with rest mass \(m\) (where \(M>2m\)). The maximum value of the momentum that any one of the lighter particles can have in a direction perpendicular to the \(z\)-direction, is
(a)
\(\frac{1}{2}C\sqrt{M^2-4m^2}\)
(b)
\(\frac{1}{2}C\sqrt{M^2-2m^2}\)
(c)
\(C\sqrt{M^2-4m^2}\)
(d)
\(\frac{1}{2}MC\)
Check Answer
Option a
Q.No:21 CSIR Feb-2022
A monochromatic source emitting radiation with a certain frequency moves with a velocity
\(v\) away from a stationary observer \(A\) . It is moving towards another observer \(B\) (also at rest)
along a line joining the two. The frequencies of the radiation recorded by \(A\) and \(B\) are \(\nu_A\) and
\(\nu_B\) , respectively. If the ratio \(\frac{\nu_B}{\nu_A}=7\), then the value of \(v/c\) is
(1)
\(1/2\)
(2)
\(1/4\)
(3)
\(3/4\)
(4)
\(\sqrt{3}/2\)
Check Answer
Option 3
Q.No:22 CSIR Dec-2017
In the rest frame \(\mathbf{S}_1\) of a point particle with electric charge \(q_1\), another point particle with electric charge \(q_2\) moves with a speed \(v\) parallel to the \(x\)-axis at a perpendicular distance \(l\). The magnitude of the electromagnetic force felt by \(q_1\) due to \(q_2\) when the distance between them is minimum, is [In the following \(\gamma=\frac{1}{\sqrt{1-v^2/c^2}}\).]
(1)
\(\frac{1}{4\pi \epsilon_0} \frac{q_1 q_2}{\gamma l^2}\)
(2)
\(\frac{1}{4\pi \epsilon_0} \frac{\gamma q_1 q_2}{l^2}\)
(3)
\(\frac{1}{4\pi \epsilon_0} \frac{\gamma q_1 q_2}{l^2}\left(1+\frac{v^2}{c^2}\right)\)
(4)
\(\frac{1}{4\pi \epsilon_0} \frac{q_1 q_2}{\gamma l^2}\left(1+\frac{v^2}{c^2}\right)\)
Check Answer
Option 2
Q.No:23 CSIR Dec-2018
In an inertial frame, uniform electric and magnetic fields \(\vec{E}\) and \(\vec{B}\) are perpendicular to each other and satisfy \(|\vec{E}|^2-|\vec{B}|^2=29\) (in suitable units). In another inertial frame, which moves at a constant velocity with respect to the first frame, the magnetic field is \(2\sqrt{5}\hat{k}\). In the second frame, an electric field consistent with the previous observations is
(1)
\(\frac{7}{\sqrt{2}}(\hat{i}+\hat{j})\)
(2)
\(7(\hat{i}+\hat{k})\)
(3)
\(\frac{7}{\sqrt{2}}(\hat{i}+\hat{k})\)
(4)
\(7(\hat{i}+\hat{j})\)
Check Answer
Option 1
Q.No:24 Assam CSIR Dec-2019
Let \(\vec{E}(\vec{r}, t)\) and \(\vec{B}(\vec{r}, t)\) denote, respectively, the electric and magnetic fields at a point \(\vec{r}\) at time \(t\), due to the motion of a massive particle of charge \(+q\) moving along the positive \(x\)-axis with a speed \(v\). Then, in \(CGS\) units, for all values of \(v\)
(1)
\(|\vec{E}|< c|\vec{B}|\)
(2)
\(|\vec{E}|> c|\vec{B}|\)
(3)
\(|\vec{E}|= c|\vec{B}|\)
(4)
\(|\vec{E}|= \frac{c}{\sqrt{1-\frac{v^2}{c^2}}}|\vec{B}|\)
Check Answer
Option 2
Q.No:25 CSIR June-2016
The values of the electric and magnetic fields in a particular reference frame (in Gaussian units) are \(\mathbf{E}=3\hat{x}+4\hat{y}\) and \(\mathbf{B}=3\hat{z}\), respectively. An inertial observer moving with respect to this frame measures the magnitude of the electric field to be \(|\mathbf{E}'|=4\). The magnitude of the magnetic field \(|\mathbf{B}'|\) measured by him is
(1)
\(5\)
(2)
\(9\)
(3)
\(0\)
(4)
\(1\)
Check Answer
Option 3
Q.No:26 CSIR June-2019
An inertial observer A at rest measures the electric and magnetic field \(\mathbf{E}=(\alpha, 0, 0)\) and \(\mathbf{B}=(\alpha, 0, 2\alpha)\) in a region, where \(\alpha\) is a constant. Another inertial observer B, moving with a constant velocity with respect to A, measures the fields as \(\mathbf{E}'=(E_x', \alpha, 0)\) and \(\mathbf{B}'=(\alpha, B_y', \alpha)\). Then, in units \(c=1\), \(E_x'\) and \(B_y'\) are given, respectively, by
(1)
\(-2\alpha\) and \(\alpha\)
(2)
\(2\alpha\) and \(-\alpha\)
(3)
\(\alpha\) and \(-2\alpha\)
(4)
\(-\alpha\) and \(2\alpha\)
Check Answer
Option 4
Q.No:27 CSIR June-2020
The electric field due to a uniformly charged infinite line along the \(z\)-axis, as observed in the rest frame \(S\) of the line charge, is \(\vec{E}(\vec{r})=\frac{\lambda}{2\pi \in_0} \frac{x\hat{i}+y\hat{j}}{(x^2+y^2)}\). In a frame \(M\) moving with a constant speed \(\nu\) with respect to \(S\) along the \(z\)-direction, the electric field \(\vec{E'}\) is (in the following \(\beta=\nu/c\) and \(\gamma=1/\sqrt{1-\beta^2}\))
(1)
\(E_x'=E_x\) and \(E_y'=E_y\)
(2)
\(E_x'=\beta \gamma E_x\) and \(E_y'=\beta \gamma E_y\)
(3)
\(E_x'=E_x/\gamma\) and \(E_y'=E_y/\gamma\)
(4)
\(E_x'=\gamma E_x\) and \(E_y'=\gamma E_y\)
Check Answer
Option 4
Q.No:28 CSIR Sep-2022
A particle of rest mass \(m\) is moving with a velocity \(v\hat{k}\), with respect to initial frame \(S\). The energy of the particle as measured by an observer \(S'\), who is moving with a uniform velocity \(u\hat{i}\) with respect to \(S\) (in terms of \(\gamma_u=1/\sqrt{1-u^2/c^2}\) and \(\gamma_v=1/\sqrt{1-v^2/c^2}\)) is
(1)
\(\gamma_u\gamma_vm(c^2-uv)\)
(2)
\(\gamma_u\gamma_vmc^2\)
(3)
\(\frac{1}{2}(\gamma_u +\gamma_v)mc^2\)
(4)
\(\frac{1}{2}(\gamma_u +\gamma_v)m(c^2-uv)\)
Check Answer
Option 2
Q.No:29 CSIR June-2023
The charge density and current of an infinitely long perfectly conducting wire of radius \(a\), which lies along the z-axis, as measured by a static are zero and a constant \(I\), respectively. The charge density measured by an observer, who moves at a speed \(v=\beta c\) parallel to the wire along the direction of the current, is
1) \(-\frac{I\beta}{\pi a^2c\sqrt{1-\beta^2}}\)
2) \(-\frac{I\beta\sqrt{1-\beta^2}}{\pi a^2c}\)
3) \(\frac{I\beta}{\pi a^2c\sqrt{1-\beta^2}}\)
4) \(\frac{I\beta\sqrt{1-\beta^2}}{\pi a^2c}\)
Check Answer
Option 1
Q.No:30 CSIR Dec-2023
The coordinates of the following events in an observer's inertial frame of reference are as follows:
Event 1: \( t_1 = 0 \), \( x_1 = 0 \) : A rocket with uniform velocity \(0.5c\) crosses the observer at origin along x axis
Event 2: \( t_2 = T \), \( x_2 = 0 \) : The observer sends a light pulse towards the rocket
Event 3: \( t_3, x_3 \) : The rocket receives the light pulse
The values of \( t_3, x_3 \) respectively are
1) \( 2T, cT \)
2) \( 2T, \frac{cT}{2} \)
3) \( \frac{\sqrt{3}}{2} T, \frac{2cT}{\sqrt{3}} \)
4) \( \frac{2T}{\sqrt{3}}, \frac{\sqrt{3}cT}{2} \)
Check Answer
Option 1
Q.No:31 CSIR June-2024
A square plate of dimension \(a \times a\) makes an angle \(\theta = \pi/4\) with the \(x\) axis in its rest frame \(S\) as shown in the figure.
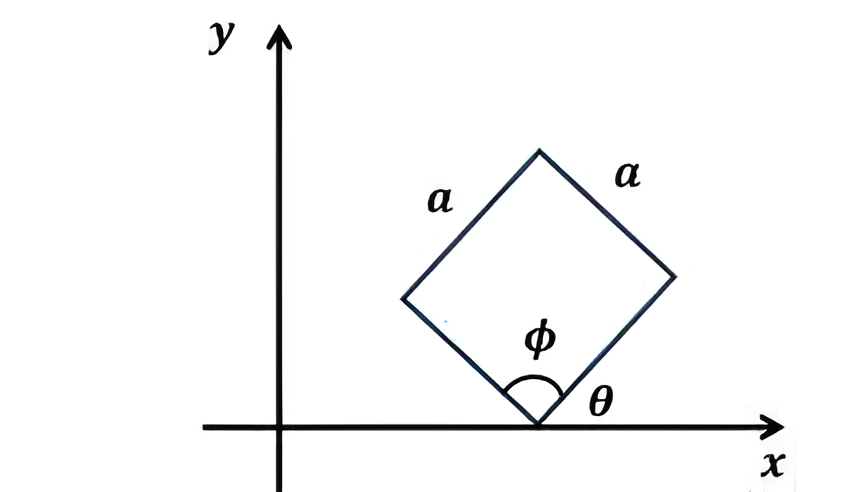
It is moving with a speed \(v = \frac{\sqrt{3}}{2} c\) along the \(x\) axis with respect to an observer \(S'\) (where \(c\) is the speed of light in vacuum). The value of the interior angle \(\phi\) indicated in the figure (which is obviously \(\pi/2\) in the frame \(S\)), as measured in \(S'\) is:
1) \(\frac{\pi}{3}\)
2) \(\frac{2\pi}{3}\)
3) \(\frac{\pi}{6}\)
4) \(\frac{4\pi}{3}\)
Check Answer
Option 1
Q.No:32 CSIR Dec-2024
A certain elementary particle is created in the upper atmosphere. It then moves
downward with speed \( v = 0.9999\,c \) with respect to an observer on Earth.
Its lifetime in its rest frame is \( 2 \times 10^{-6} \,\text{s} \).
The distance (in the Earth's frame) travelled by the elementary particle
before it decays is closest to
1) \( 0.6 \,\text{km} \)
2) \( 42 \,\text{km} \)
3) \( 12 \,\text{km} \)
4) \( 72 \,\text{km} \)
Check Answer
Option 2
Q.No:33 CSIR Dec-2024
A particle of rest mass \( m_0 \) and energy \( E \) collides with another particle
at rest, having the same rest mass.
What is the minimum value of \( E \) such that after the collision,
there may be four particles each of rest mass \( m_0 \)?
1) \( 4 m_0 c^2 \)
2) \( 3 m_0 c^2 \)
3) \( 7 m_0 c^2 \)
4) \( 16 m_0 c^2 \)
Check Answer
Option 3
Q.No:34 CSIR June -2025
In a particular inertial frame, the electric and magnetic fields are
\(\vec{E} = E_0 \,\hat{x}\), \(\vec{B} = \frac{E_0}{2c}\,\hat{x}\).
Which of the following statements is true?
1) There exists an inertial frame where \(\vec{E} = 0\), \(\vec{B} \neq 0\)
2) There exists no inertial frame where either \(\vec{E} = 0\) or \(\vec{B} = 0\)
3) There exists an inertial frame where \(\vec{B} = 0\), \(\vec{E} \neq 0\)
4) There exists an inertial frame where both \(\vec{E} = 0\) and \(\vec{B} = 0\)
Check Answer
Option 2
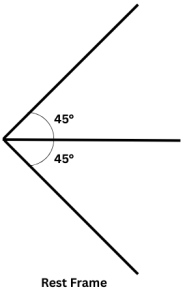
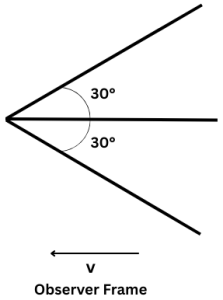
Q.No:35 CSIR June -2025
In its rest frame, a source emits light in a conical beam of angular width
from \(-45^\circ\) to \(+45^\circ\).
An observer is moving towards the source with speed \(v\).
For the observer, the beam width appears reduced to
from \(-30^\circ\) to \(+30^\circ\).
The speed of the observer is closest to:
1) \(0.62\,c\)
2) \(0.50\,c\)
3) \(0.82\,c\)
4) \(0.41\,c\)
