Q.No:1 JEST-2012
In a certain inertial frame two light pulses are emitted at points \(5 km\) apart and separated in time by \(5 \mu s\). An observer moving at a speed \(V\) along the line joining these points notes that the pulses are simultaneous. Therefore \(V\) is
(a)
\(0.7c\)
(b)
\(0.8c\)
(c)
\(0.3c\)
(d)
\(0.48l_0\)
Check Answer
Option c
Q.No:2 JEST-2013
In an observer's rest frame, a particle is moving towards the observer with an energy \(E\) and momentum \(p\). If \(c\) denotes the velocity of light in vacuum, the energy of the particle in another frame moving in the same direction as the particle with a constant velocity \(v\) is
(a)
\(\frac{(E+vp)}{\sqrt{1-(v/c)^2}}\)
(b)
\(\frac{(E-vp)}{\sqrt{1-(v/c)^2}}\)
(c)
\(\frac{(E+vp)}{[1-(v/c)^2]^2}\)
(d)
\(\frac{(E-vp)}{[1-(v/c)^2]^2}\)
Check Answer
Option b
Q.No:3 JEST-2013
A light beam is propagating through a block of glass with index of refraction \(n\). If the glass is moving at constant velocity \(v\) in the same direction as the beam, the velocity of the light in the glass block as measured by an observer in the laboratory is approximately
(a)
\(u=\frac{c}{n}+v\left(1-\frac{1}{n^2}\right)\)
(b)
\(u=\frac{c}{n}-v\left(1-\frac{1}{n^2}\right)\)
(c)
\(u=\frac{c}{n}+v\left(1+\frac{1}{n^2}\right)\)
(d)
\(u=\frac{c}{n}\)
Check Answer
Option a
Q.No:4 JEST-2013
Under a Galilean transformation, the coordinates and momenta of any particle/system transform as: \(t'=t, \vec{r}'=\vec{r}+\vec{v}t\) and \(\vec{p'}=\vec{p}+m\vec{v}\), where \(\vec{v}\) is the velocity of the boosted frame with respect to the original frame. A unitary operator carrying out these transformations for a system having total mass \(M\), total momentum \(\vec{P}\) and center of mass coordinate \(\vec{X}\) is
(a)
\(e^{iM\vec{v}.\vec{X}/\hbar} e^{it\vec{v}.\vec{P}/\hbar}\)
(b)
\(e^{iM\vec{v}.\vec{X}/\hbar} e^{-it\vec{v}.\vec{P}/\hbar} e^{-iMv^2 t/(2\hbar)}\)
(c)
\(e^{iM\vec{v}.\vec{X}/\hbar} e^{it\vec{v}.\vec{P}/\hbar} e^{iMv^2 t/(2\hbar)}\)
(d)
\(e^{it\vec{v}.\vec{P}/\hbar} e^{-iMv^2 t/(2\hbar)}\)
Check Answer
Option b
Q.No:5 JEST-2013
The velocity of a particle at which the kinetic energy is equal to its rest energy is (in terms of \(c\), the speed of light in vacuum)
(a)
\(\sqrt{3}c/2\)
(b)
\(3c/4\)
(c)
\(\sqrt{3/5}c\)
(d)
\(c/\sqrt{2}\)
Check Answer
Option a
Q.No:_ JEST-2013
Under a Galilean transformation, the coordinates and momenta of any particle/system transform as: \(t'=t, \vec{r}'=\vec{r}+\vec{v}t\) and \(\vec{p'}=\vec{p}+m\vec{v}\), where \(\vec{v}\) is the velocity of the boosted frame with respect to the original frame. A unitary operator carrying out these transformations for a system having total mass \(M\), total momentum \(\vec{P}\) and center of mass coordinate \(\vec{X}\) is
a) \(e^{iM\vec{v}.\vec{X}/\hbar} e^{it\vec{v}.\vec{P}/\hbar}\)
b) \(e^{iM\vec{v}.\vec{X}/\hbar} e^{-it\vec{v}.\vec{P}/\hbar} e^{-iMv^2 t/(2\hbar)}\)
c) \(e^{iM\vec{v}.\vec{X}/\hbar} e^{it\vec{v}.\vec{P}/\hbar} e^{iMv^2 t/(2\hbar)}\)
d) \(e^{it\vec{v}.\vec{P}/\hbar} e^{-iMv^2 t/(2\hbar)}\)
Check Answer
Option b
Q.No:6 JEST-2014
In a certain inertial frame two light pulses are emitted, a distance \(5 km\) apart and separated by \(5 \mu s\). An observer who is traveling, parallel to the line joining the points where the pulses are emitted, at a velocity \(V\) with respect to this frame notes that the pulses are simultaneous. Therefore \(V\) is
(a)
\(0.7c\)
(b)
\(0.8c\)
(c)
\(0.3c\)
(d)
\(0.9c\)
Check Answer
Option c
Q.No:7 JEST-2014
A monochromatic wave propagates in a direction making an angle \(60^{\circ}\) with the \(x\)-axis in the reference frame of source. The source moves at speed \(\nu=\frac{4c}{5}\) towards the observer. The direction of the (cosine of angle) wave as seen by the observer is
(a)
\(\cos{\theta'}=\frac{13}{14}\)
(b)
\(\cos{\theta'}=\frac{3}{14}\)
(c)
\(\cos{\theta'}=\frac{13}{6}\)
(d)
\(\cos{\theta'}=\frac{1}{2}\)
Check Answer
Option a
Q.No:8 JEST-2015
The distance of a star from the Earth is \(4.25\) light years, as measured from the Earth. A space ship travels from Earth to the star at a constant velocity in \(4.25\) years, according to the clock on the ship. The speed of the space ship in units of the speed of light is,
(a)
\(\frac{1}{2}\)
(b)
\(\frac{1}{\sqrt{2}}\)
(c)
\(\frac{2}{3}\)
(d)
\(\frac{1}{\sqrt{3}}\)
Check Answer
Option b
Q.No:9 JEST-2016
Light takes approximately \(8\) minutes to travel from the Sun to the Earth. Suppose in the frame of the Sun an event occurs at \(t=0\) at the Sun and another event occurs on Earth at \(t=1\) minute. The velocity of the inertial frame in which both these events are simultaneous is:
(A)
\(c/8\) with the velocity vector pointing from Earth to Sun
(B)
\(c/8\) with the velocity vector pointing from Sun to Earth
(C)
The events can never be simultaneous - no such frame exists
(D)
\(c\sqrt{1-\left(\frac{1}{8}\right)^2}\) with velocity vector pointing from Sun to Earth
Check Answer
Option B
Q.No:10 JEST-2018
A person on Earth observes two rockets \(A\) and \(B\) directly approaching each other with speeds \(0.8c\) and \(0.6c\) respectively. At a time when the distance between the rockets is observed to be \(4.2\times 10^8
m\), the clocks of the rockets and the Earth are synchronized to \(t=0 s\). The time of collision (in seconds) of the two rockets as measured in rocket \(A\)'s frame is \(x/10\). What is \(x\)?
A's frame is x/10. What is x?
Check Answer
Ans 6
Q.No:11 JEST-2019
An optical line of wavelength \(5000\) Angstroms. in the spectrum of light from a star is found to be red-shifted by an amount of \(2\) Angstroms. Let \(v\) be the velocity at which the star is receding. Ignoring relativistic effects, what is the value of \(\frac{c}{v}\)?
Check Answer
Ans 2500 OR 2501
Q.No:12 JEST-2021
A spaceship moves away from Earth with a relativistic speed \(v\) and fires a shuttle craft in the forward direction at a speed \(v\) relative to the spaceship. The pilot of the shuttle craft launches a probe in the forward direction at a speed \(v\) relative to the shuttle craft. What will be the speed of the probe relative to the Earth?
(A)
\(3v\)
(B)
\(\frac{3v}{\sqrt{1-v^2/c^2}}\)
(C)
\(\left(\frac{3+v^2/c^2}{1+3v^2/c^2}\right)v\)
(D)
\(\frac{2v}{1+v^2/c^2}+v\)
Check Answer
Option C
Q.No:13 JEST-2021
A binary star system consists of two stars with same mass \(M\) revolving about a common centre of mass in a circular orbit with velocities much smaller than the speed of light, \(c=3.0\times 10^8 \text{m/s}\). The axis of the plane of rotation is perpendicular to our line of sight. The wavelength of a particular spectral line from one of the stars is observed to change with a period of \(2.40\times 10^5\) seconds. If the ratio of maximum to minimum wavelength of the line is \(1.0022\), the distance between the stars (in \(10^9 \text{m}\)) to the nearest integer, is
Check Answer
Ans 25
Q.No:14 JEST-2022
The front-end of a train moving with constant acceleration, passes a pole with velocity \(u\), and its back-end passes the pole with velocity \(v\). With what velocity does the mid-point of this train pass the same pole?
(a)
\(\sqrt{\frac{u^2+v^2}{2}}\)
(b)
\(\frac{1}{2}\sqrt{u^2+v^2}\)
(c)
\(\frac{uv}{u+v}\)
(d)
\(\frac{u+v}{2}\)
Check Answer
Option a
Q.No:14 JEST-2023
A beam of light is propagating through a block of glass with refractive index \(n\). The block is moving with a constant speed \(v\) in the direction opposite to that of the beam. The speed of the light beam in the block as measured by an observer in the laboratory frame is:
A) \(\frac{c}{2n}\)
B) \(\frac{c}{n}\)
C) \(\frac{c}{2n}\)
D) \(\frac{c-nv}{n-\frac{v}{c}}\)
Check Answer
Option d
Q.No:15 JEST-2023
A rocket is moving in free space with speed \(\frac{c}{2}\). After a fuel tank is gently detached, the rocket is found to be moving with a speed \(\frac{c}{4}\) with respect to the detached fuel tank. What is the final
speed of the rocket in the original frame of reference?
A) \(\frac{2}{7} c\)
B) \(\frac{2}{3} c\)
C) \(\frac{3}{4} c\)
D) \(\frac{4}{5} c\)
Check Answer
Option b
Q.No:16 JEST-2023
A stationary body explodes into two fragments, each of rest mass \(m\). The two fragments move apart at speeds \(\eta c\) (where \(c\) is the speed of light and \(0< \eta <1\)) relative to the original body.
The rest mass of the original body is:
A) \(2m \sqrt{1-\eta^2}\)
B) \(2m (1-\eta^2)\)
C) \(\frac{2m }{\sqrt{1-\eta^2}}\)
D) \(2m\)
Check Answer
Option C
Q.No:17 JEST-2024
Two trains, each having proper length \( L_0 \) are moving towards each other with the same speed \( v \) but in opposite directions as measured by an observer in an inertial frame. What is the length of one of the trains as measured by an observer in the other train?
A) \( L_0 \frac{(c^2 - v^2)}{(c^2 + v^2)} \)
B) \( L_0 \sqrt{\frac{(c^2 - v^2)}{(c^2 + v^2)}} \)
C) \( L_0 \sqrt{1 - \frac{v^2}{4c^2}} \)
D) \( L_0 \sqrt{1 - \frac{v^2}{c^2}} \)
Check Answer
Option C
Q.No:18 JEST-2025
For a relativistic point particle, the momentum is given by
\(\vec{p} = \frac{m_0 \vec{v}}{\sqrt{1 - v^2/c^2}}\),
where \(\vec{v}\) is its velocity as measured by an inertial observer.
Then the acceleration is in the same direction as the applied force:
A) always.
B) only when the force is neither parallel nor perpendicular to the velocity.
C) only when the force is parallel or perpendicular to the velocity.
D) never.
Check Answer
Option C
Q.No:19 JEST-2025
A particle is moving with velocity components \(v_x = v_y = v_z = c/2\) in frame \(S\).
The ratio of the velocity component \(v_y\) to the velocity component \(v'_y\),
as measured in frame \(S'\) moving with velocity \(c/2\) with respect to frame \(S\)
along the common \(x\)-direction, is
A) \(\sin(\pi/6)\)
B) \(\cos(\pi/6)\)
C) \(\sin(\pi/3)\)
D) \(\cos(\pi/3)\)
Check Answer
Option B
Q.No:20 JEST-2025
The average lifetime of a muon in its rest frame is \(2200\ \text{ns}\).
What will be the average distance (in meters, to the nearest integer)
travelled by it, when created with a velocity of \(\frac{1}{3}c\),
before it decays? Here \(c\) is the speed of light.
Check Answer
ANS 233
Q.No:1 TIFR-2013
A spaceship \(S\) blasts off from the Earth. After some time, Earth station informs the crew that they have settled into a constant velocity \(0.28c\) radially outward from the Earth, but unfortunately they are on a head-on collision course with an asteroid \(A\) at a distance of \(15\) light-minutes coming in towards the Earth along the same radius (see figure below).

Instruments on-board the spaceship immediately estimate the speed of the asteroid to have a constant value \(0.24c\). It follows that the maximum time (in minutes) available to the crew to evacuate the ship before the collision is
(a)
\(60\)
(b)
\(30\)
(c)
\(29\)
(d)
\(63\)
Check Answer
Option a
Q.No:2 TIFR-2013
Which of the following classic experiments provides unambiguous proof that the Earth is a non-inertial frame of reference with respect to the fixed stars?
(a)
Fizeau's rotating wheel experiment
(b)
Foucault's pendulum experiment
(c)
Newton's coin-and-feather experiment
(d)
Michelson-Morley experiment
Check Answer
Option b
Q.No:3 TIFR-2014
In the laboratory frame, two observers A and B are moving along the sides of an equilateral triangle with equal speeds \(c/2\), as shown in the figure.

The speed of B as measured by A will be
(a)
\(\frac{\sqrt{3}}{2}c\)
(b)
\(\frac{4}{3\sqrt{3}}c\)
(c)
\(\frac{\sqrt{13}}{7}c\)
(d)
\(\frac{\sqrt{5}}{3}c\)
Check Answer
Option d
Q.No:4 TIFR-2014
Cosmic ray muons generated at the top of the Earth's atmosphere decay according to the radioactive decay law
\[
N(t)=N(0)\exp{\left(-\frac{0.693t}{T_{1/2}}\right)}
\]
where \(N(t)\) is the number of muons at time \(t\), and \(T_{1/2}=1.52 \mu s\) is the proper half-life of the muon. Immediately after generation, most of these muons shoot down towards the Earth's surface. Some of these muons decay on the way, but their interaction with the atmosphere is negligible.
An observer on the top of a mountain of height \(2.0 km\) above mean sea level detects muons with the speed \(0.98c\) over a period of time and counts \(1000\) muons. The number of muons of the same speed detected by an observer at mean sea level in the same period of time would be
(a)
\(232\)
(b)
\(539\)
(c)
\(839\)
(d)
\(983\)
Check Answer
Option b
Q.No:5 TIFR-2015
A light beam is propagating through a medium with index of refraction \(1.5\). If the medium is moving at constant velocity \(0.7c\) in the same direction as the beam, what is the velocity of light in the medium as measured by an observer in the laboratory? (\(c=\) velocity of light in vacuum)
(a)
\(0.93c\)
(b)
\(0.98c\)
(c)
\(0.96c\)
(d)
\(0.9c\)
Check Answer
Option a
Q.No:6 TIFR-2015
A collimated beam of pions originate from an accelerator and propagates in vacuum along a long straight beam pipe. The intensity of this beam was measured in the laboratory after a distance of \(75 m\) and found to have dropped to one-fourth of its intensity at the point of origin. If the proper half-life of a pion is \(1.77\times 10^{-8} s\), the speed of the pions in the beam, as measured in the laboratory, must be
(a)
\(0.99c\)
(b)
\(0.98c\)
(c)
\(0.97c\)
(d)
\(0.96c\)
Check Answer
Option a
Q.No:7 TIFR-2016
In a glass fibre, light propagates by total internal reflection from the inner surface. A very short pulse of light enters a perfectly uniform glass fibre at \(t=0\) and emerges from the other end of the fibre with negligible losses. If the refractive index of the glass used in the fibre is \(1.5\) and its length is exactly \(1.0 km\), the time \(t\) at which the output pulse will have completely exited the fibre will be
(a)
\(5.0 \mu s\)
(b)
\(7.5 \mu s\)
(c)
\(25 ns\)
(d)
\(750 ns\)
Check Answer
Option d
Q.No:8 TIFR-2016
In a futuristic scenario, two spaceships, A and B, are running a race, where they start from the same point (marked START) but fly in opposite directions at constant speeds close to the speed of light. An observer fixed at the starting point observes that they both cross the points marked END, which are equidistant from the starting point, at the same time. Afterwards this observer receives messages from both spaceships.
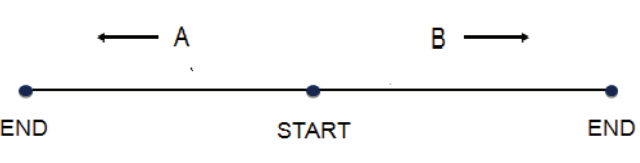
Which of the following could be true?
(a)
Both A and B agree that A won the race.
(b)
A and B both claim to have won the race.
(c)
Both A and B agree that they crossed the end point simultaneously.
(d)
A thinks B won the race while B thinks A won the race.
Check Answer
Option b
Q.No:9 TIFR-2018
From an observational post \(E\) on the Earth, two ballistic missiles, each of rest length \(\ell\) from nose-tip to tail-end, are observed to fly past each other, with the same uniform relativistic speed \(c/2\), in opposite directions, as shown below.
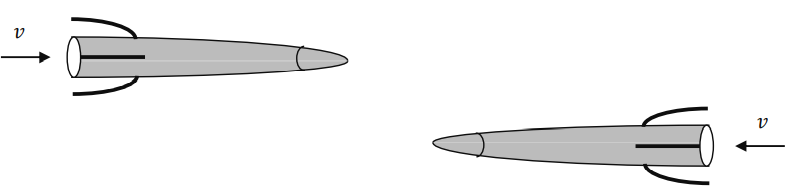
Check Answer
Ans
Q.No:10 TIFR-2018
If the velocity of the Earth in its orbit is \(\nu\), find \(\partial E/E\), where \(E\) is the translational (non-relativistic) kinetic energy of the Earth and \(\delta E\) is its relativistic correction to the lowest order in \(\nu/c\).
Check Answer
Ans
Q.No:11 TIFR-2020
A particle of rest mass \(\sqrt{3}\hspace{1mm}\text{g}\) emerges from a gun with a velocity \(\nu=c/4\). If the rest mass of the gun is \(1\hspace{1mm}\text{kg}\), its approximate speed of recoil will be
(a)
\(c/1000\)
(b)
\(c/2236\)
(c)
\(c/1732\)
(d)
\(c/2309\)
Check Answer
Option b
Q.No:12 TIFR-2020
In the laboratory frame, a particle at rest starts moving with a speed \(c/2\) from one corner of a square (see figure) and traverses the four sides of the square so that it returns to its original position. At each corner, it changes direction without any change in speed.
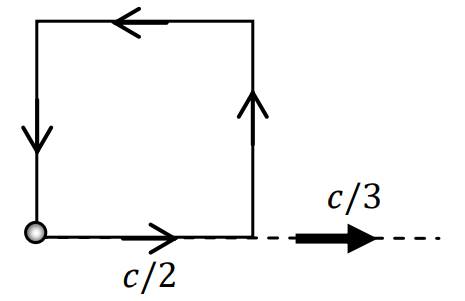
If the entire square now moves with a speed \(c/3\) in the laboratory frame, as indicated in the figure, the speed of the particle (in the laboratory frame) when it returns to its original position will be
(a)
\(\frac{2\sqrt{2}c}{15}\)
(b)
\(\frac{c}{5}\)
(c)
\(\frac{2\sqrt{2}c}{3}\)
(d)
\(\frac{c}{5\sqrt{3}}\)
Check Answer
Option a
Q.No:13 TIFR-2021
In a futuristic scenario, an inter-planetary meeting is arranged on planet Pegasus XIV, which is \(10\) light years away from the Earth. The team of representatives from Earth would like to take a spaceship to Pegasus XIV that has a one-hour flight time according to the watches of the passengers. The Team Leader from Earth would like to leave from the Earth half-an-hour later, but taking a spaceship that has a half-an-hour flight time according to the watches of the passengers. If the time taken for acceleration may be neglected for both spaceships, which of the following statements is correct?
(a)
The Team Leader would reach Pegasus XIV before the committee members.
(b)
The Team Leader would reach Pegasus XIV at the same time as the committee members.
(c)
The Team Leader would reach Pegasus XIV after the committee members.
(d)
The situation described in the problem is not possible by the laws of physics.
Check Answer
Option a
Q.No:14 TIFR-2022
An observer O, moving with relativistic speed \(v\) away from a fixed plane mirror M in a line perpendicular to the mirror surface, sends a pulse of light of wavelength \(\lambda\) towards the mirror.

The wavelength of the light reflected back to the observer will be
(a)
\(\lambda (\frac{c+v}{c-v})\)
(b)
\(\lambda (\frac{c+2v}{c-2v})\)
(c)
\(\lambda \sqrt{\frac{c+v}{c-v}}\)
(d)
\(\lambda (\frac{c-2v}{c+2v})\)
Check Answer
Option a
Q.No:15 TIFR-2023
A relativistic particle, moving in a dimension x, starts from rest at \(x=0\) and is subjected to a uniform and constant force field along the positive x-direction. If the dashed line corresponds at \(x=ct\), which of the following curves (red line) would be represent the position \(x(t)\) of the particle?

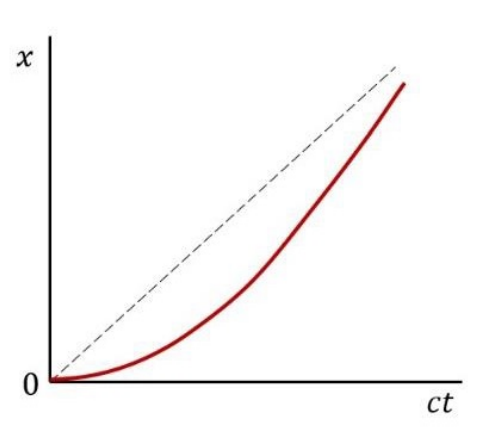
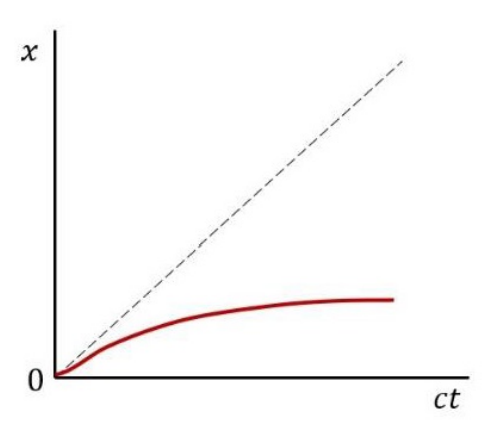
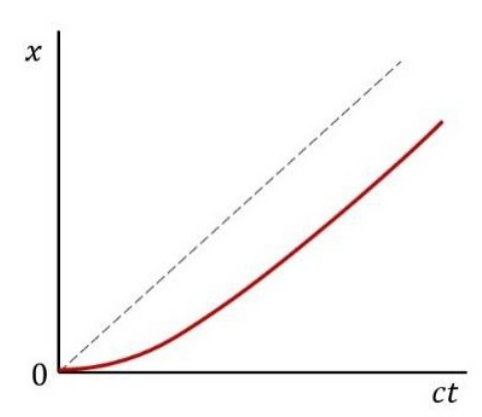
Check Answer
Option d
Q.No:16 TIFR-2024
Consider a spaceship \( S \) of length \( L \) is moving relativistically in the \( x \) direction with a speed \( v_x \) relative to an inertial reference frame \( F \) as shown in the figure. In \( S \), a light bulb is placed at the left end (point \( A \)) and a detector is placed at the right end (point \( B \)). What is the time taken for light to travel from \( A \) to \( B \) in the reference frame \( F \)?
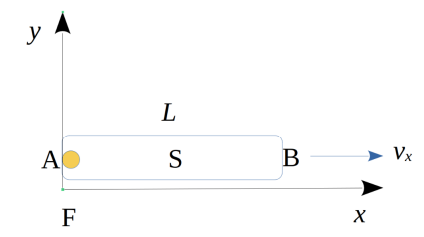
(a) \( \frac{L}{c} \sqrt{\frac{1 + v_x/c}{1 - v_x/c}} \)
(b) \( \frac{L}{c} \sqrt{\left( 1 - \frac{v_x^2}{c^2} \right)} \)
(c) \( \frac{L}{c} \sqrt{\frac{1 - v_x/c}{1 + v_x/c}} \)
(d) \( \frac{L}{c} \frac{1}{\sqrt{1 - v_x^2/c^2}} \)
Check Answer
Option a
Q.No:17 TIFR-2024
A massive particle moving at a speed of \( \frac{4c}{5} \) collides with an identical particle at rest. What would be the speed of the second particle in the center-of-mass frame after the collision?
(a) \( \frac{c}{2} \)
(b) \( \frac{2c}{5} \)
(c) \( \frac{c}{\sqrt{2}} \)
(d) \( \frac{2\sqrt{2}c}{5} \)
Check Answer
Option a
Q.No:18 TIFR-2025
Consider the following space–time diagram which indicates three events
\(A\), \(B\), and \(C\) for an inertial observer.
Which of the following statements is true?
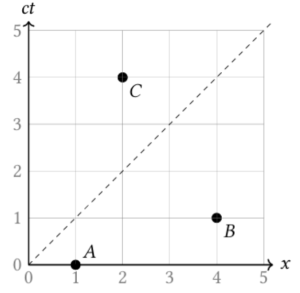
a) It is always possible to find an inertial observer for whom events
\(A\) and \(B\) are simultaneous. However, no inertial observer can be
found for whom events \(A\) and \(C\) are simultaneous.
b) It is always possible to find an inertial observer for whom events
\(A\) and \(C\) are simultaneous. However, no inertial observer can be
found for whom events \(A\) and \(B\) are simultaneous.
c) It is always possible to find an inertial observer for whom events
\(A\) and \(B\) are simultaneous. Similarly, an inertial observer can
also be found for whom events \(A\) and \(C\) are simultaneous.
d) It is impossible to find an inertial observer for whom events
\(A\) and \(B\) are simultaneous. Similarly, no inertial observer can
be found for whom events \(A\) and \(C\) are simultaneous.
Check Answer
Option a
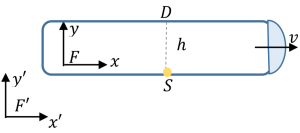
Q.No:19 TIFR-2025
A spaceship is moving with a constant relativistic velocity \(v \hat{x}'\)
with respect to an inertial frame \(F'\).
In the frame \(F\) moving with the spaceship, light is emitted from a source
\(S\) and is detected at the detector \(D\), which is displaced from \(S\)
by \(h\)\(\hat{y}\).
In the frame \(F'\), what is the time \(t'\) taken for the light to travel
from \(S\) to \(D\)?
a) \(\frac{h/c}{\sqrt{1 - v^{2}/c^{2}}}\)
b) \(\left(\frac{h}{c}\right)\sqrt{1 - \frac{v^{2}}{c^{2}}}\)
c) \(\left(\frac{h}{c}\right)\sqrt{\frac{1 - v/c}{1 + v/c}}\)
d) \(\frac{h}{c}\)
Check Answer
Option a
Q.No:20 TIFR-2025
Consider two relativistic particles, each with mass \(m\) and momentum of magnitude \(p\),
colliding head-on. As a result of the collision, two heavier particles are produced,
each with mass \(\alpha m\), where \(\alpha > 1\).
What is the minimum value of \(p\) required for this collision to occur?
a) \(\sqrt{\alpha^{2} - 1}\, mc\)
b) \((\alpha - 1)mc\)
c) \(2\alpha mc\)
d) \((\sqrt{\alpha} - 1)^{2} mc\)
