Q.No:1 GATE-2012
Total binding energies of \({O^{15}}\), \({O^{16}}\) and \({O^{17}}\) are \(111.96 MeV, 127.62 MeV\) and \(131.76 MeV\), respectively. The energy gap between \(1p_{1/2}\) and \(1d_{5/2}\) neutron shells for the nuclei whose mass number is close to \(16\), is
(A)
\(4.1 MeV\)
(B)
\(11.5 MeV\)
(C)
\(15.7 MeV\)
(D)
\(19.8 MeV\)
Check Answer
Option B
Q.No:2 GATE-2013
In the Schmidt model of nuclear magnetic moments, we have,
\[
\vec{\mu}=\frac{e\hbar}{2Mc} (g_l\vec{l}+g_S\vec{S})
\]
where the symbols have their usual meaning
For the case \(J=l+1/2\), where \(J\) is the total angular momentum, the expectation value of \(\vec{S}\cdot \vec{J}\) in the nuclear ground state is equal to,
(A)
\((J-1)/2\)
(B)
\((J+1)/2\)
(C)
\(J/2\)
(D)
\(-J/2\)
Check Answer
Option B
Q.No:3 GATE-2013
In the Schmidt model of nuclear magnetic moments, we have,
\[
\vec{\mu}=\frac{e\hbar}{2Mc} (g_l\vec{l}+g_S\vec{S})
\]
where the symbols have their usual meaning
For the \({O^{17}}\) nucleus (\(A=17, Z=8\)), the effective magnetic moment is given by,
\[
\vec{\mu}_{eff}=\frac{e\hbar}{2Mc} g\vec{J},
\]
where \(g\) is equal to, (\(g_s=5.59\) for proton and \(-3.83\) for neutron)
(A)
\(1.12\)
(B)
\(-0.77\)
(C)
\(-1.28\)
(D)
\(1.28\)
Check Answer
Option B
Q.No:4 GATE-2015
In the nuclear shell model, the potential is modeled as \(V(r)=\frac{1}{2} m\omega^2 r^2-\lambda \vec{L}\cdot \vec{S}\), \(\lambda>0\). The correct spin-parity and isospin assignments for the ground state of \({^{13} C}\) is
(A)
\(\frac{1}{2}^{-}; \frac{-1}{2}\)
(B)
\(\frac{1}{2}^{+}; \frac{-1}{2}\)
(C)
\(\frac{3}{2}^{+}; \frac{1}{2}\)
(D)
\(\frac{3}{2}^{-}; \frac{-1}{2}\)
Check Answer
Option A
Q.No:5 GATE-2016
According to the nuclear shell model, the respective ground state spin-parity values of \({^{15}_{8} O}\) and \({^{17}_{8} O}\) nuclei are
(A)
\(\frac{1}{2}^{+}, \frac{1}{2}^{-}\)
(B)
\(\frac{1}{2}^{-}, \frac{5}{2}^{+}\)
(C)
\(\frac{3}{2}^{-}, \frac{5}{2}^{+}\)
(D)
\(\frac{3}{2}^{-}, \frac{1}{2}^{-}\)
Check Answer
Option B
Q.No:6 GATE-2017
\(J^P\) for the ground state of the \({^{13} C_{6}}\) nucleus is
(A)
\(1^{+}\)
(B)
\(\frac{3}{2}^{-}\)
(C)
\(\frac{3}{2}^{+}\)
(D)
\(\frac{1}{2}^{-}\)
Check Answer
Option D
Q.No:7 GATE-2018
An \(\alpha\) particle is emitted by a \({^{230}_{90} Th}\) nucleus. Assuming the potential to be purely Coulombic beyond the point of separation, the height of the Coulomb barrier is ____________ MeV (up to two decimal places).
(\(\frac{e^2}{4\pi \epsilon_0}=1.44 MeV-fm, r_0=1.30 fm\))
Check Answer
Ans 24.5-27.6
Q.No:8 GATE-2019
The nuclear spin and parity of \({^{40}_{20} Ca}\) in its ground state is
(A)
\(0^{+}\)
(B)
\(0^{-}\)
(C)
\(1^{+}\)
(D)
\(1^{-}\)
Check Answer
Option A
Q.No:9 GATE-2020
According to the Fermi gas model of the nucleus, the nucleons move in a spherical volume of radius \(R\) (\(=R_0 A^{\frac{1}{3}}\), where \(A\) is the mass number and \(R_0\) is an empirical constant with the dimensions of length). The Fermi energy of the nucleus \(E_F\) is proportional to
(A)
\(R_0^2\)
(B)
\(\frac{1}{R_0}\)
(C)
\(\frac{1}{R_0^2}\)
(D)
\(\frac{1}{R_0^3}\)
Check Answer
Option C
Q.No:10 GATE-2020
The total angular momentum \(j\) of the ground state of the \({^{17}_{8} O}\) nucleus is
(C)
\(\frac{1}{2}\)
(C)
\(1\)
(C)
\(\frac{3}{2}\)
(C)
\(\frac{5}{2}\)
Check Answer
Option D
Q.No:11 GATE-2021
The Coulomb energy component in the binding energy of a nucleus is \(18.432 MeV\). If the radius of the uniform and spherical charge distribution in the nucleus is \(3 fm\), the corresponding atomic number (rounded off to the nearest integer) iS _________________.
Given: \(\frac{e^2}{4\pi \epsilon_0}=1.44 MeV fm\))
Check Answer
Ans 8 OR 9
Q.No:12 GATE-2022
If nucleons in a nucleus are considered to be confined in a three-dimensional cubical box, then the first four magic numbers are
(a)
\(2, 8, 20, 28\)
(b)
\(2, 10, 16, 28\)
(c)
\(2, 8, 14, 20\)
(d)
\(2, 10, 16, 28\)
Check Answer
Option c
Q.No:13 GATE-2022
In a nucleus, the interaction \(V_{SO}\vec{l}\cdot \vec{s}\) is responsible for creating spin-orbit doublets. The energy difference between \(p_{1/2}\) and \(p_{3/2}\) states in units of \(V_{SO}\frac{\hbar^2}{2}\) is ---------- (Round off to the nearest integer)
Check Answer
Ans 3
Q.No:14 GATE-2024
According to the nuclear shell model, the absolute value of the difference in magnetic moments of \( ^{15}_8O \) and \( ^{15}_7N \), in the units of nuclear magneton \( (\mu_N) \) is \( a/3 \). The magnitude of \( a \) is _____ (in integer).
Check Answer
Ans 2
Q.No:15 GATE-2025
The nuclear energy levels of mirror nuclei are similar. Using this empirical fact alone, the nuclear force can be said to be independent of which one of the following properties of the nucleons?
A) Mass
B) Spin
C) Charge
D) Parity
Check Answer
Option c
Q.No:1 CSIR Dec-2014
If the binding energy \(B\) of a nucleus (mass number \(A\) and charge \(Z\)) is given by
\[
B=a_V A-a_S A^{2/3}-a_{\text{sym}} \frac{(2Z-A)^2}{A}-\frac{a_C Z^2}{A^{1/3}}
\]
where \(a_V=16 MeV, a_S=16 MeV, a_{\text{sym}}=24 MeV\) and \(a_C=0.75 MeV\), then the \(Z\) for the most stable isobar for a nucleus with \(A=216\) is
(1)
\(68\)
(2)
\(72\)
(3)
\(84\)
(4)
\(92\)
Check Answer
Option 3
Q.No:2 CSIR June-2015
Let us approximate the nuclear potential in
the shell model by a three dimensional isotropic harmonic oscillator. Since the lowest two energy levels have angular momenta \(l = 0\) and \(l = 1\) respectively, which of the following two nuclei have magic numbers of proyons and neutrons?
(1)
\({ }_{4}^{2} \mathrm{He}\) and \({ }_{16}^{8} \mathrm{O}\)
(2)
\({ }_{2}^{1} \mathrm{D}\) and \({ }_{8}^{4} \mathrm{Be}\)
(3)
\({ }_{4}^{2} \mathrm{He}\) and \({ }_{8}^{4} \mathrm{Be}\)
(4)
\({ }_{4}^{2} \mathrm{He}\) and \({ }_{12}^{6} \mathrm{O}\)
Check Answer
Option 1
Q.No:3 CSIR Dec-2015
The electric quadrupole moment of an odd proton nucleus is \(\frac{(2j-1)}{2(j+1)}\langle r^2\rangle\), where \(j\) is the total angular momentum. Given that \(R_0=1.2 \text{ fm}\), what is the value, in barn, of the quadrupole moment of the \({^{27}Al}\) nucleus in the shell model?
(1)
\(0.043\)
(2)
\(0.023\)
(3)
\(0.915\)
(4)
\(0\)
Check Answer
Option 1
Q.No:4 CSIR Dec-2015
Of the nuclei of mass number \(A=125\), the binding energy calculated from the liquid drop model (given that the coefficients for the Coulomb and the asymmetry energy are \(a_C=0.7 \text{ MeV}\) and \(a_{sym}=22.5 \text{ MeV}\) respectively) is a maximum for
(1)
\({^{125}_{54}Xe}\)
(2)
\({^{125}_{53}I}\)
(3)
\({^{125}_{52}Te}\)
(4)
\({^{125}_{51}Sb}\)
Check Answer
Option 3
Q.No:5 CSIR June-2016
Let \(E_S\) denote the contribution of the surface energy per nucleon in the liquid drop model. The ratio \(E_S({^{27}_{13}Al}):E_S\hspace{1mm}({^{64}_{30}Zn})\) is
(1)
\(2:3\)
(2)
\(4:3\)
(3)
\(5:3\)
(4)
\(3:2\)
Check Answer
Option 2
Q.No:6 CSIR June-2016
According to the shell model, the nuclear magnetic moment of the \({^{27}_{13}Al}\) nucleus is (Given that for a proton \(g_l=1, g_s=5.586\), and for a neutron \(g_l=0, g_s=-3.826\).)
(1)
\(-1.913 \mu_N\)
(2)
\(14.414 \mu_N\)
(3)
\(4.793 \mu_N\)
(4)
\(0\)
Check Answer
Option 3
Q.No:7 CSIR Dec-2017
The spin-parity assignments for the ground and first excited states of the isotope \({^{57}_{28} Ni}\), in the single particle shell model, are
(1)
\((1/2)^{-}\) and \((3/2)^{-}\)
(2)
\((5/2)^{+}\) and \((7/2)^{+}\)
(3)
\((3/2)^{+}\) and \((5/2)^{+}\)
(4)
\((3/2)^{-}\) and \((5/2)^{-}\)
Check Answer
Option 4
Q.No:8 CSIR Dec-2019
The Bethe-Weizsacker formula for the binding energy (in MeV) of a nucleus of atomic number \(Z\) and mass number \(A\) is
\[
15.8A-18.3A^{2/3}-0.714\frac{Z(Z-1)}{A^{1/3}}-23.2\frac{(A-2Z)^2}{A}
\]
The ratio \(Z/A\) for the most stable isobar of a \(A=64\) nucleus, is nearest to
(1)
\(0.30\)
(2)
\(0.35\)
(3)
\(0.45\)
(4)
\(0.50\)
Check Answer
Option 3
Q.No:9 Assam CSIR Dec-2019
The Bethe-Weizsacker formula for the binding energy of a heavy even-even nucleus with \(Z\) protons and \(N\) neutrons is \(BE=a_V A-a_S A^{2/3}-a_C \frac{Z^2}{A^{1/3}}-a_A \frac{(N-Z)^2}{A}\), where \(A\) is the mass number and \(a_V, a_S, a_C\) and \(a_A\) are constants. When it spontaneously breaks up into two equal fragments, the total energy released is
(1)
\(-\frac{1}{2}a_V A+a_S A^{\frac{2}{3}}\left(1-2^{\frac{1}{3}}\right)+\frac{1}{4}a_a A^{-1}(N-Z)^2\)
(2)
\(a_S A^{\frac{2}{3}}\left(1-2^{\frac{1}{3}}\right)+a_C Z^2 A^{-\frac{1}{3}}\left(1-2^{-\frac{1}{3}}\right)+\frac{1}{4}a_a A^{-1}(N-Z)^2\)
(3)
\(a_S A^{\frac{2}{3}}\left(1-2^{\frac{1}{3}}\right)+a_C Z^2 A^{-\frac{1}{3}}\left(1-2^{-\frac{2}{3}}\right)\)
(4)
\(-\frac{1}{2}a_V A+a_S A^{\frac{2}{3}}\left(1-2^{\frac{1}{3}}\right)+a_C Z^2 A^{-\frac{1}{3}}\left(1-2^{-\frac{1}{3}}\right)\)
Check Answer
Option 3
Q.No:10 CSIR June-2020
The binding energy \(B\) of a nucleus is approximated by the formula \(B=a_1 A-a_2 A^{2/3}-a_3 Z^2 A^{-1/3}-a_4(A-2Z)^2 A^{-1}\), where \(Z\) is the atomic number and \(A\) is the mass number of the nucleus. If \(\frac{a_4}{a_2}\simeq 30\). The atomic number \(Z\) for naturally stable isobars (constant value of \(A\)) is
(a)
\(\frac{30A}{60+A^{2/3}}\)
(b)
\(\frac{30A}{30+A^{2/3}}\)
(c)
\(\frac{60A}{120+A^{2/3}}\)
(d)
\(\frac{120A}{60+A^{2/3}}\)
Check Answer
Option c
Q.No:11 CSIR June-2020
The magnetic moments of a proton and a neutron are \(2.792 \mu_N\) and \(-1.913 \mu_N\), where \(\mu_N\) is the nucleon magnetic moment. The values of the magnetic moments of the mirror nuclei \({^{19}_{9} F_{10}}\) and \({^{19}_{10} Ne_{9}}\), respectively, in the Shell model, are closest to
(a)
\(23.652 \mu_N\) and \(-18.873 \mu_N\)
(b)
\(26.283 \mu_N\) and \(-16.983 \mu_N\)
(c)
\(-2.628 \mu_N\) and \(1.887 \mu_N\)
(d)
\(2.628 \mu_N\) and \(-1.887 \mu_N\)
Check Answer
Option d
Q.No:12 CSIR Dec-2023
In a shell model description, neglecting Coulomb effects, which of the following statements for the energy and spin-parity is correct for the first excited state of \( A = 12 \) isobars \( ^{12}_{\ 5}B \), \( ^{12}_{\ 6}C \), and \( ^{12}_{\ 7}N \)?
1) same for \( ^{12}_{\ 5}B \), \( ^{12}_{\ 6}C \) and \( ^{12}_{\ 7}N \)
2) different for each \( ^{12}_{\ 5}B \), \( ^{12}_{\ 6}C \) and \( ^{12}_{\ 7}N \)
3) same for \( ^{12}_{\ 6}C \) and \( ^{12}_{\ 7}N \), but different for \( ^{12}_{\ 5}B \)
4) same for \( ^{12}_{\ 5}B \) and \( ^{12}_{\ 7}N \), but different for \( ^{12}_{\ 6}C \)
Check Answer
Option 4
Q.No:1 JEST-2015
The stable nucleus that has \(\frac{1}{3}\) the radius of \({^{189} Os}\) nucleus is,
(a)
\(Li\)
(b)
\({^{16} O}\)
(c)
\({^{4} He}\)
(d)
\({^{14} N}\)
Check Answer
Option a
Q.No:1 TIFR-2015
In the semi-empirical mass formula, the volume (\(V\)), surface (\(S\)), coulomb (\(C\)), and pairing (\(P\)) contributions to the binding energy of a nucleus \({}^A_Z X\) vary with mass number \(A\) as
(a)
\(V\propto A, S\propto A^{2/3}, C\propto A^{-1/3}, P\propto A^{-3/4}\)
(b)
\(V\propto A, S\propto A^{1/3}, C\propto A^{-1/3}, P\propto A^{-3/4}\)
(c)
\(V\propto A, S\propto A^{-2/3}, C\propto A^{1/3}, P\propto A^{-3/4}\)
(d)
\(V\propto A^2, S\propto A^{2/3}, C\propto A^{-1/3}, P\propto A^{-3/4}\)
Check Answer
Option a
Q.No:2 TIFR-2017
In a theoretical model of the nucleus, the binding energy per nucleon was predicted as shown in the figure below.
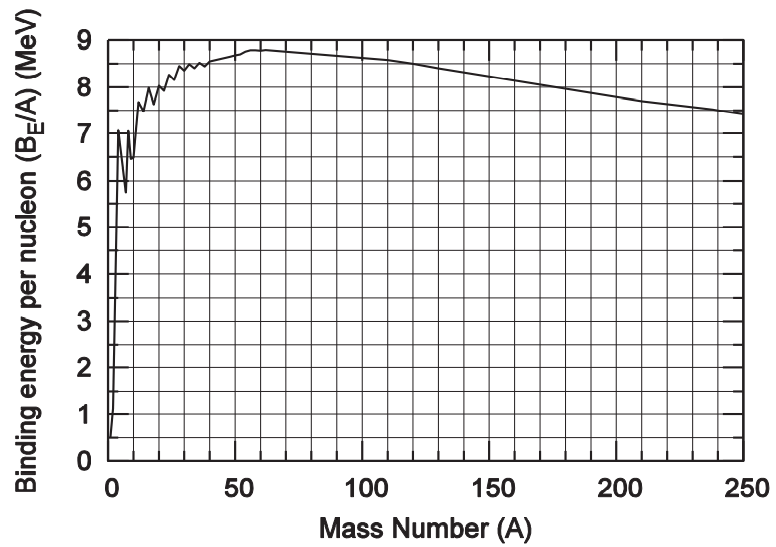
If a nucleus of mass number \(A=240\) undergoes a symmetric fission to two daughter nuclei each of mass number \(A=120\), write down the amount of energy released in this process, in units of \(\text{MeV}\), using this theoretical model.
Check Answer
Ans 240
Q.No:3 TIFR-2019
The semi-empirical mass formula for a heavy nucleon \((Z, A)\) can be written, to some approximation, as
\[
M(Z, A)c^2=ZM_p c^2+(A-Z)M_n c^2-\lambda_1 A-\lambda_2 A^{2/3}-\lambda_3\frac{Z(Z-1)}{A^{1/3}}-
\]
\[
\lambda_4\frac{(A-2Z)^2}{A}-\frac{\lambda_5}{A^{1/2}}
\]
where \(M_p c^2=938 \hspace{1mm}\text{MeV}, M_n c^2=939 \hspace{1mm}\text{MeV}\), and
\[
\lambda_1=16, \lambda_2=18, \lambda_3=0.7, \lambda_4=23,
\]
all in \(\text{MeV}\), where
\[
\lambda_5=
\left\{
\begin{array}{ll}
+12 & \text{MeV for even--even nuclei} \\
-12 & \text{MeV for odd--odd nuclei} \\
0 & \text{for others} \\
\end{array}
\right.
\]
Now, consider a spontaneous fission reaction
\[
{^{238}_{92} U}\to {^{146}_{56} Ba}+{^{91}_{36} Kr}+{^{1}_{0}n}
\]
The energy released in this reaction will be close to
(a)
\(17.92 \hspace{1mm}\text{keV}\)
(b)
\(19.2 \hspace{1mm}\text{keV}\)
(c)
\(170 \hspace{1mm}\text{keV}\)
(d)
\(190 \hspace{1mm}\text{keV}\)
Check Answer
Option d
Q.No:4 TIFR-2022
In the shell model of the nucleus, it is known that orbitals get filled in the order
\[1s_{1/2} \hspace{3mm} 1p_{3/2} \hspace{3mm} 1p_{1/2} \hspace{3mm} 1d_{5/2} \hspace{3mm} 2s_{1/2} \hspace{3mm}1d_{3/2} \hspace{3mm} \text{and so on}\]
For a nucleus of \(_8 ^{18} O \) the two neutrons outside the doubly-magic core of \(_8 ^{16} O \) will occupy the same orbital. The allowed value of \(J^p\) will be
(a)
\(4^+\)
(b)
\(5^+\)
(c)
\(2^-\)
(d)
\(3^+\)
Check Answer
Option a
Q.No:5 TIFR-2023
The binding energy \(\epsilon_b\) of a nuclide \(^Z _A X\) with automic number \(Z\) and mass number \(A\) is given by the semi -empirical formula
\[\epsilon_b=a-V A-a_S A^{2/3}-a_C \frac{Z(Z-1)}{A^{1/3}}+a_A \frac{(A-2Z)^2}{A}\]
where the constant parameters and source for effect for each term are
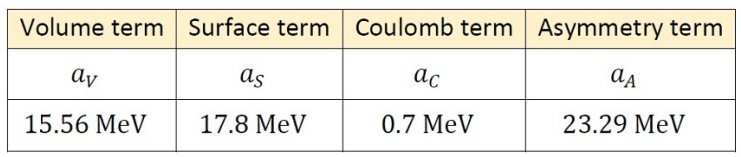
What is the mass difference between the two-mirror nuclei \(^{13}_6 C \) and \(^{13}_7 N \)? It is known that both of them are spherical in shape and have a uniform charge distribution.
(a)
0.78 MeV
(b)
1.84 MeV
(c)
2.62 MeV
(d)
3.40 MeV
Check Answer
Option c
Q.No:6 TIFR-2023
The binding energy \(\epsilon_b\) of a nuclide \(^Z _A X\) with automic number \(Z\) and mass number \(A\) is given by the semi-empirical formula
\[\epsilon_b=a_V A -a_S A^{2/3}-a_C\frac{Z(Z-1)}{A^{1/3}}+a_A\frac{(A-2Z)^2}{A}\]
where the constant parameters and source for effect for each term are
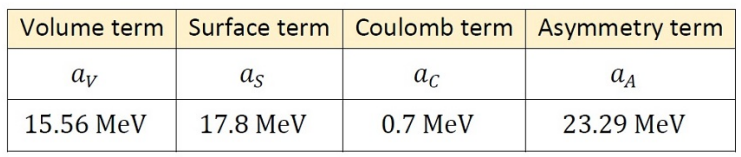
For a spherical neutron star containing of only neutron and having uniform nuclear density throughout its volume, the Columb term is replaced by gravitational energy. What would be the smallest radius of this neutron star?
(a)
10.435 km
(b)
4.345 km
(c)
2.165 km
(d)
4.345 m
Check Answer
Option b
Q.No:7 TIFR-2024
Oxygen (O) nuclei (\( Z = 8 \)) can be approximated as non-interacting protons and neutrons filling up orbitals in the following order.
\[ 1s_{1/2}, 1p_{3/2}, 1p_{1/2}, 1d_{5/2}, 2s_{1/2}, 1d_{3/2}, \ldots \]
where the subscript specifies the \( J \) quantum number. Given the binding energy of O (\( A = 15 \)) is 111.96 MeV, O (\( A = 16 \)) is 127.62 MeV, and O (\( A = 17 \)) is 131.76 MeV, what is the difference between the energies of the \( 1p_{1/2} \) and the \( 1d_{5/2} \) orbitals?
(a) 11.52 MeV
(b) 15.66 MeV
(c) 4.14 MeV
(d) 19.81 MeV
