Q.No:1 CSIR Dec-2014
A particle of mass \(m\) is moving in the potential \(V(x)=-\frac{1}{2}ax^2+\frac{1}{4}bx^4\) where \(a, b\) are positive constants. The frequency of small oscillations about a point of stable equilibrium is
(1)
\(\sqrt{a/m}\)
(2)
\(\sqrt{2a/m}\)
(3)
\(\sqrt{3a/m}\)
(4)
\(\sqrt{6a/m}\)
Check Answer
Option 2
Q.No:2 CSIR June-2015
A particle of mass m moves in the one dimensional potential \(V(x) = \frac{\alpha}{3}x^{3} + \frac{\beta}{4}x^{4}\) where \(\alpha, \beta > 0\). One of the equilibrium points is \(x = 0\). The angular frequency of small oscillations about the other equilibrium point is
(1)
\(\frac{2a}{\sqrt{3m\beta}}\)
(2)
\(\frac{\alpha}{\sqrt{m \beta}}\)
(3)
\(\frac{\alpha}{\sqrt{12m \beta}}\)
(4)
\(\frac{\alpha}{\sqrt{24m \beta}}\)
Check Answer
Option 2
Q.No:3 CSIR Dec-2015
The Lagrangian of a system is given by \(L=\frac{1}{2}m\dot{q_1}^2+2m\dot{q_2}^2-k\left(\frac{5}{4}q_1^2+2q_2^2-2q_1 q_2\right)\) where \(m\) and \(k\) are positive constants. The frequencies of its normal modes are
(1)
\(\sqrt{\frac{k}{2m}}, \sqrt{\frac{3k}{m}}\)
(2)
\(\sqrt{\frac{k}{2m}}(13\pm \sqrt{73})\)
(3)
\(\sqrt{\frac{5k}{2m}}, \sqrt{\frac{k}{m}}\)
(4)
\(\sqrt{\frac{k}{2m}}, \sqrt{\frac{6k}{m}}\)
Check Answer
Option 1
Q.No:4 CSIR June-2017
A solid vertical rod, of length \(L\) and cross-sectional area \(A\), is made of a material of Young's modulus \(Y\). The rod is loaded with a mass \(M\), and, as a result, extends by a small amount \(\Delta L\) in the equilibrium condition. The mass is then suddenly reduced to \(M/2\). As a result the rod will undergo longitudinal oscillation with an angular frequency
(1)
\(\sqrt{2YA/ML}\)
(2)
\(\sqrt{YA/ML}\)
(3)
\(\sqrt{2YA/M\Delta L}\)
(4)
\(\sqrt{YA/M\Delta L}\)
Check Answer
Option 1
Q.No:5 CSIR June-2018
A particle of mass \(m\), kept in a potential \(V(x)=-\frac{1}{2}kx^2+\frac{1}{4}\lambda x^4\) (where \(k\) and \(\lambda\) are positive constants), undergoes small oscillations about an equilibrium point. The frequency of oscillations is
(1)
\(\frac{1}{2\pi}\sqrt{\frac{2\lambda}{m}}\)
(2)
\(\frac{1}{2\pi}\sqrt{\frac{k}{m}}\)
(3)
\(\frac{1}{2\pi}\sqrt{\frac{2k}{m}}\)
(4)
\(\frac{1}{2\pi}\sqrt{\frac{\lambda}{m}}\)
Check Answer
Option 3
Q.No:6 CSIR Dec-2019
The time period of a particle of mass \(m\), undergoing small oscillations around \(x=0\), in the potential \(V=V_0\cosh{\left(\frac{x}{L}\right)}\), is
(1)
\(\pi\sqrt{\frac{mL^2}{V_0}}\)
(2)
\(2\pi\sqrt{\frac{mL^2}{2V_0}}\)
(3)
\(2\pi\sqrt{\frac{mL^2}{V_0}}\)
(4)
\(2\pi\sqrt{\frac{2mL^2}{V_0}}\)
Check Answer
Option 3
Q.No:7 CSIR June-2019
Two particles of masses \(m_1\) and \(m_2\) are connected by a massless thread of length \(\ell\) as shown in figure below.
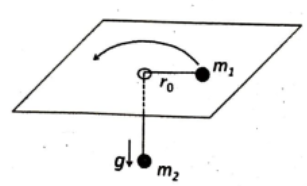
The particle of mass \(m_1\) on the plane undergoes a circular motion with radius \(r_0\) and angular momentum \(L\). When a small radial displacement \(\epsilon\) (where \(\epsilon \ll r_0\)) is applied, its radial coordinate is found to oscillate about \(r_0\). The frequency of the oscillations is
(1)
\(\sqrt{\frac{7m_2 g}{\left(m_1+\frac{m_2}{2}\right)r_0}}\)
(2)
\(\sqrt{\frac{7m_2 g}{\left(m_1+m_2\right)r_0}}\)
(3)
\(\sqrt{\frac{3m_2 g}{\left(m_1+\frac{m_2}{2}\right)r_0}}\)
(4)
\(\sqrt{\frac{3m_2 g}{\left(m_1+m_2\right)r_0}}\)
Check Answer
Option 4
Q.No:8 CSIR June-2019
The equation of motion of a forced simple harmonic oscillator is \(\ddot{x}+\omega^2 x=A\cos{\Omega t}\), where \(A\) is a constant. At resonance \(\Omega=\omega\), the amplitude of oscillations at large times
(1)
saturates to a finite value
(2)
increases with time as \(\sqrt{t}\)
(3)
increases linearly with time
(4)
increases exponentially with time
Check Answer
Option 3
Q.No:9 CSIR June-2020
A pendulum executes small oscillations between angles \(+\theta_0\) and \(-\theta_0\). If \(\tau(\theta) d\theta\) is the time spent between \(\theta\) and \(\theta+d\theta\), then \(\tau(\theta)\) is best represented by


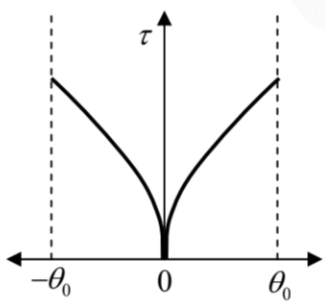
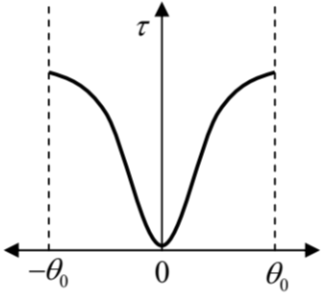
Check Answer
Option b
Q.No:10 CSIR Sep-2022
The Lagrangian of a system of two particles is
\[
L= \frac{1}{2} \dot{x_1}^2 + 2
\dot{x_2}^2 - \frac{1}{2}
(x_1^2 + x_2^2 + x_1 x_2)\]
The normal frequencies are best approximated by
(1)
1.2 and 0.7
(2)
1.5 and 0.5
(3)
1.7 and 0.5
(4)
1.0 and 0.4
Check Answer
Option 4
Q.No:11 CSIR June-2023
A system of two identical masses connected by identical springs, as shown in the figure, oscillates along the vertical direction.
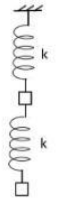
The ratio of frequencies of normal modes is
1) \(\sqrt{3-\sqrt{5}} : \sqrt{3+\sqrt{5}}\)
2) \(3-\sqrt{5} : 3+\sqrt{5}\)
3) \(\sqrt{5-\sqrt{3}} : \sqrt{5+\sqrt{3}}\)
4) \(5-\sqrt{3} : 5+\sqrt{3}\)
Check Answer
Option 1
Q.No:12 CSIR Dec-2023
A particle of unit mass subjected to the 1-dimensional potential
\[
V(x) = \frac{2\alpha}{x^3} - \frac{3\beta}{x^2}
\]
executes small oscillations about its equilibrium position, where \( \alpha \) and \( \beta \) are positive constants with appropriate dimensions. The time period of small oscillations is
1) \( \frac{\pi\alpha^2}{\sqrt{6\beta^5}} \)
2) \( \frac{\pi\alpha^2}{\sqrt{3\beta^5}} \)
3) \( \frac{2\pi\alpha^2}{\sqrt{3\beta^5}} \)
4) \( \frac{2\pi\alpha^2}{\sqrt{6\beta^5}} \)
Check Answer
Option 4
Q.No:13 CSIR June-2024
Three identical simple pendula (of mass \(m\) and equilibrium string length \(l\)) are attached together by springs of spring constant \(k\), as shown in the figure.

The frequencies of small oscillations are given by \(\sqrt{\frac{g}{l}}, \sqrt{\frac{k}{m} + \frac{g}{l}}, \sqrt{\frac{3k}{m} + \frac{g}{l}}\). The normal modes (without normalisation) corresponding to these frequencies respectively are
1) \((1, 1, 1), (1, 0, 1), (1, -2, 1)\)
2) \((1, 1, 1), (1, 0, -1), (1, 2, 1)\)
3) \((1, 1, 1), (1, 0, -1), (1, -2, 1)\)
4) \((1, 2, 1), (1, 1, 1), (1, 1, 1)\)
Check Answer
Option 3
Q.No:14 CSIR June-2024
A linear molecule is modelled as two atoms of equal mass \( m \) placed at coordinates \( x_1 \) and \( x_2 \), connected by a spring of spring constant \( k \). The molecule is moving in one dimension under an additional external potential \( V(x_1, x_2) = \frac{1}{2} m \omega_0^2 (x_1^2 + x_2^2) \). If one frequency of molecular vibration is \( \omega_0 \), the other frequency is:
1) \( \sqrt{\omega_0^2 - \frac{k}{m}} \)
2) \( \sqrt{\omega_0^2 + \frac{k}{m}} \)
3) \( \sqrt{\omega_0^2 + \frac{2k}{m}} \)
4) \( \sqrt{\omega_0^2 - \frac{2k}{m}} \)
Check Answer
Option 3
Q.No:1 GATE-2012
A particle of unit mass moves along the \(x\)-axis under the influence of a potential, \(V(x)=x(x-2)^2\). The particle is found to be in stable equilibrium at the point \(x=2\). The time period of oscillation of the particle is
(A)
\(\frac{\pi}{2}\)
(B)
\(\pi\)
(C)
\(\frac{3\pi}{2}\)
(D)
\(2\pi\)
Check Answer
Option B
Q.No:2 GATE-2013
Consider two small blocks, each of mass \(M\), attached to two identical springs. One of the springs is attached to the wall, as shown in the figure. The spring constant of each spring is \(k\). The masses slide along the surface and the friction is negligible. The frequency of one of the normal modes of the system is,

(A)
\(\sqrt{\frac{3+\sqrt{2}}{2}} \sqrt{\frac{k}{M}}\)
(B)
\(\sqrt{\frac{3+\sqrt{3}}{2}} \sqrt{\frac{k}{M}}\)
(C)
\(\sqrt{\frac{3+\sqrt{5}}{2}} \sqrt{\frac{k}{M}}\)
(D)
\(\sqrt{\frac{3+\sqrt{6}}{2}} \sqrt{\frac{k}{M}}\)
Check Answer
Option C
Q.No:3 GATE-2014
Two masses m and \(3 m\) are attached to the two ends of a massless spring with force constant \(K\). If \(m=100 g\) and \(K=0.3 N/m\), then the natural angular frequency of oscillation is _______________Hz.
Check Answer
Ans 1.99-2.01
Q.No:4 GATE-2014
A particle of mass \(m\) is in a potential given by
\[
V(r)=-\frac{a}{r}+\frac{ar_0^2}{3r^3},
\]
where \(a\) and \(r_0\) are positive constants. When disturbed slightly from its stable equilibrium position, it undergoes a simple harmonic oscillation. The time period of oscillation is
(A)
\(2\pi \sqrt{\frac{mr_0^3}{2a}}\)
(B)
\(2\pi \sqrt{\frac{mr_0^3}{a}}\)
(C)
\(2\pi \sqrt{\frac{2mr_0^3}{a}}\)
(D)
\(4\pi \sqrt{\frac{mr_0^3}{a}}\)
Check Answer
Option A
Q.No:5 GATE-2016
Two blocks are connected by a spring of spring constant \(k\). One block has mass \(m\) and the other block has mass \(2m\). If the ratio \(k/m=4 s^{-2}\), the angular frequency of vibration \(\omega\) of the two block spring system in \(s^{-1}\) is ___________. (Give your answer upto two decimal places)
Check Answer
Ans 2.41-2.49
Q.No:6 GATE-2017
Two identical masses of \(10 gm\) each are connected by a massless spring of spring constant \(1 N/m\). The non-zero angular eigenfrequency of the system is _________ rad/s. (up to two decimal places).
Check Answer
Ans 14.10-14.20
Q.No:7 GATE-2018
In the context of small oscillations, which one of the following does NOT apply to the (it normal coordinates)?
(A)
Each normal coordinate has an eigen-frequency associated with it
(B)
The normal coordinates are orthogonal to one another
(C)
The normal coordinates are all independent
(D)
The potential energy of the system is a sum of squares of the normal coordinates with constant coefficients
Check Answer
Option B
Q.No:8 GATE-2020
The potential energy of a particle of mass \(m\) is given by
\[
U(x)=a\sin{(k^2 x-\pi/2)}, a>0, k^2>0.
\]
The angular frequency of small oscillations of the particle about \(x=0\) is
(A)
\(k^2 \sqrt{\frac{2a}{m}}\)
(B)
\(k^2 \sqrt{\frac{a}{m}}\)
(C)
\(k^2 \sqrt{\frac{a}{2m}}\)
(D)
\(2k^2 \sqrt{\frac{a}{m}}\)
Check Answer
Option B
Q.No:9 GATE-2024
Lagrangian of a particle of mass \( m \) is \( L = \frac{1}{2}m\dot{x}^2 - \lambda x^4 \), where \( \lambda \) is a positive constant. If the particle oscillates with total energy \( E \), then the time period of oscillations is
\[
a \int_{0}^{\left(\frac{E}{\lambda}\right)^{\frac{1}{4}}} \frac{dx}{\sqrt{\left(\frac{2}{m}\right)(E - \lambda x^4)}}
\]
The value of \( a \) is _____ (in integer).
Check Answer
Ans 4
Q.No:10 GATE-2025
The figure shows a system of two equal masses \(m\) and three massless horizontal springs with spring constants \(k_1, k_2, k_1\).
Ignore gravity. The masses can move only in the horizontal direction and there is no dissipation.
If \(m = 1\), \(k_1 = 2\) and \(k_2 = 3\) (all in appropriate units),
the frequencies of the normal modes of the system in the same system of units are
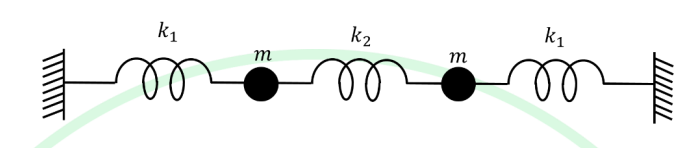
A) \(\sqrt{2}, \sqrt{8}\)
B) \(\sqrt{2}, \sqrt{6}\)
C) \(\sqrt{3}, \sqrt{10}\)
D) \(\sqrt{3}, \sqrt{8}\)

Q.No.1 Discussion (CSIR) :
Q.No.2 Discussion (CSIR) :
Q2 CSIR
Q.No.3 Discussion (CSIR) :
My solution for question 3 csir net
Q.No.4 Discussion (CSIR) :
Answer
Q4
Q.No.5 Discussion (CSIR) :
Ans
Q.No.6 Discussion (CSIR) :
Ans
Q.No.7 Discussion (CSIR) :
Q.No.8 Discussion (CSIR) :
My sol
Q.No.9 Discussion (CSIR) :
My sol
Q.No.10 Discussion (CSIR) :
My sol
Q.No.11 Discussion (CSIR) :
Q.No.12 Discussion (CSIR) :
Q.No.13 Discussion (CSIR) :
Q.No.14 Discussion (CSIR) :
Q.No.1 Discussion (GATE) :
Q.No.2 Discussion (GATE) :
Q.No.3 Discussion (GATE) :
Ans
Q.No.4 Discussion (GATE) :
Ans
Q.No.5 Discussion (GATE) :
Angular frequency: 2.449
Q.No.6 Discussion (GATE) :
Angular frequency: 14.141
Q.No.7 Discussion (GATE) :
Q.No.8 Discussion (GATE) :
Answer: B
Q.No.9 Discussion (GATE) :
Q.No.10 Discussion (GATE) :