Q.No:30 JAM-2019
The Fermi-Dirac distribution function [\(n(\epsilon)\)] is
(\(k_B\) is the Boltzmann constant, \(T\) is the temperature and \(\epsilon_F\) is the Fermi energy)
(A)
\(n(\epsilon)=\frac{1}{e^{\frac{\epsilon -\epsilon_F}{k_b T}}-1}\)
(B)
\(n(\epsilon)=\frac{1}{e^{\frac{\epsilon_F -\epsilon}{k_b T}}-1}\)
(C)
\(n(\epsilon)=\frac{1}{e^{\frac{\epsilon -\epsilon_F}{k_b T}}+1}\)
(D)
\(n(\epsilon)=\frac{1}{e^{\frac{\epsilon_F -\epsilon}{k_b T}}+1}\)
Check Answer
Option C
Q.No:31 JAM-2019
In a heat engine based on the Carnot cycle, heat is added to the working substance at constant
(A)
Entropy
(B)
Pressure
(C)
Temperature
(D)
Volume
Check Answer
Option C
Q.No:32 JAM-2019
Isothermal compressibility is given by
(A)
\(\frac{1}{V}(\frac{\partial V}{\partial P})_T\)
(B)
\(\frac{1}{P}(\frac{\partial P}{\partial V})_T\)
(C)
\(-\frac{1}{V}(\frac{\partial V}{\partial P})_T\)
(D)
\(-\frac{1}{P}(\frac{\partial P}{\partial V})_T\)
Check Answer
Option C
Q.No:33 JAM-2019
A red star having radius \(r_R\) a temperature \(T_R\) and a white star having radius \(r_W\) at a temperature \(T_W\), radiate the same total power. If these stars radiate as perfect black bodies, then
(A)
\(r_R>r_W\) and \(T_R>T_W\)
(B)
\(r_R<r_W\) and \(T_R \gt T_W\)
(C)
\(r_R>r_W\) and \(T_R<T_W\)
(D)
\(r_R<r_W\) and \(T_R<T_W\)
Check Answer
Option C
Q.No:34 JAM-2019
During free expansion of an ideal gas under adiabatic condition, the internal energy of the gas
(A)
Decreases
(B)
Initially decreases and then increases
(C)
Increases
(D)
Remains constant
Check Answer
Option D
Q.No:35 JAM-2019
In the given phase diagram for a pure substance, regions I, II, III, IV, respectively represent

(A)
Vapor, Gas, Solid, Liquid
(B)
Gas, Vapor, Liquid, Solid
(C)
Gas, Liquid, Vapor, Solid
(D)
Vapor, Gas, Liquid, Solid
Check Answer
Option B
Q.No:36 JAM-2019
A thermodynamic system is described by the \(P, V, T\) coordinates. Choose the valid expression(s) for the system.
(A)
\((\frac{\partial P}{\partial V})_T (\frac{\partial V}{\partial T})_P=-(\frac{\partial P}{\partial T})_V\)
(B)
\((\frac{\partial P}{\partial V})_T (\frac{\partial V}{\partial T})_P=(\frac{\partial P}{\partial T})_V\)
(C)
\((\frac{\partial V}{\partial T})_P (\frac{\partial T}{\partial P})_V=-(\frac{\partial V}{\partial P})_T\)
(D)
\((\frac{\partial V}{\partial T})_P (\frac{\partial T}{\partial P})_V=(\frac{\partial V}{\partial P})_T\)
Check Answer
Option A,C
Q.No:37 JAM-2019
Two gases having molecular diameters \(D_1\) and \(D_2\), and mean free paths \(\lambda_1\) and \(\lambda_2\),
respectively, are trapped separately in identical containers.
If \(D_1\) = \(2D_2\), then \(\lambda_2/\lambda_1\)=______________.
(Assume there is no change in other thermodynamic parameters)
Check Answer
Ans 4
Q.No:38 JAM-2019
A di-atomic gas undergoes adiabatic expansion against the piston of a cylinder. As a result, the temperature of the gas drops from 1150 K to 400 K. The number of moles of the gas required to obtain 2300 J of work from the expansion is ___________________ .
(The gas constant \(R=8.314 \) \(J mol^{-1} K^{-1}.\) )
(Round off to 2 decimal places)
Check Answer
Ans 0.14-0.16
Q.No:39 JAM-2020
For a system undergoing a first order phase transition at a temperature \(T_c\), which one of the following graphs best describes the variation of entropy \((S)\) as a function of temperature \((T)\)?

Check Answer
Option D
Q.No:40 JAM-2020
In which one of the following limits the Fermi-Dirac distribution \(n_F(\epsilon , T)=(e^{\frac{\epsilon - \mu}{k_B T}}+1)^{-1}\) and
Bose-Einstein distribution \(n_B(\epsilon , T)=(e^{\frac{\epsilon - \mu}{k_B T}}-1)^{-1}\) reduce to Maxwell-Boltzmann distribution?
(Here \(\epsilon\) is the energy of the state, \(\mu\) is the chemical potential,\(k_B\) is the Boltzmann constant and \(T\) is
the temperature).
(A)
\(\mu =0\)
(B)
\((\epsilon - \mu) \ll k_B T\)
(C)
\((\epsilon - \mu) \gg k_B T\)
(D)
\( \mu \gg k_B T\)
Check Answer
Option C
Q.No:41 JAM-2020
Consider \(N\) classical particles at temperature \(T\), each of which can have two possible energies \(0\) and \(\epsilon\). The number of particles in the lower energy level (\(N_0\)) and higher energy level (\(N_\epsilon\)) levels are related by
(\(k_B\) is the Boltzmann constant)
(A)
\(\frac{N_0}{N_\epsilon}=e^{\frac{-\epsilon}{k_B T}}\)
(B)
\(\frac{N_0}{N_\epsilon}=e^{\frac{\epsilon}{k_B T}}\)
(C)
\(\frac{N_0}{N_\epsilon}=1+e^{\frac{\epsilon}{k_B T}}\)
(D)
\(\frac{N_0}{N_\epsilon}=1-e^{\frac{-\epsilon}{k_B T}}\)
Check Answer
Option B
Q.No:42 JAM-2020
The root mean square (rms) speeds of Hydrogen atoms at 500 K, \(V_H\), and Helium atoms at 2000 K, \(V_{HE}\) are related as
(A)
\(V_H > V_{HE}\)
(B)
\(V_H < V_{HE}\)
(C)
\(V_H = V_{HE}\)
(D)
\(V_H \gg V_{HE}\)
Check Answer
Option C
Q.No:43 JAM-2020
One mole of an ideal gas having specific heat ratio \((\gamma)\) of 1.6 is mixed with one mole of another ideal gas having specific heat ratio of 1.4. If \(C_V\) and \(C_P\) are the molar specific heat capacities of the
gas mixture at constant volume and pressure, respectively, which of the following is/are correct?
(\(R \) denotes the universal gas constant).
(A)
\(C_V=2.08\) R
(B)
\(C_P=2.9\) R
(C)
\(C_P=1.48 C_V\)
(D)
\(C_P=1.45 C_V\)
Check Answer
Option A,C
Q.No:44 JAM-2020
Consider two spherical perfect blackbodies with radii \(R_1\) and \(R_2\) at temperatures \(T_1\)= 1000 K and \(T_2\)= 2000 K, respectively. They both emit radiation of power 1 kW. The ratio of their radii, \(R_1/R_2\) is given by ___________ .
Check Answer
Ans 4
Q.No:45 JAM-2020
An ideal gas undergoes an isothermal expansion along a path AB, adiabatic expansion along BC, isobaric compression along CD, isothermal compression along DE, and adiabatic compression along EA, as shown in the figure. The work done by the gas along the process BC is 10 J. The change in the internal energy along process EA is 16 J. The absolute value of the change in the internal energy along the process CD is ________________ J.
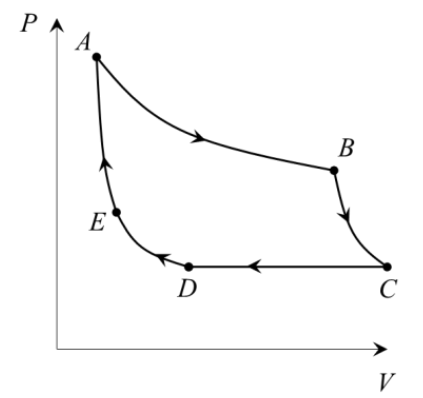
Check Answer
Ans 6
Q.No:46 JAM-2020
A body at a temperature \(T\) is brought into contact with a reservoir at temperature \(2T\). Thermal equilibrium is established at constant pressure. The heat capacity of the body at constant pressure is \(C_p\). The total change in entropy of the body and the reservoir in units of \(C_p\) is ______________ .
(Round off to 2 decimal places)
Check Answer
Ans 0.19-0.20
Q.No:47 JAM-2020
One mole of an ideal monatomic gas at pressure \(P\), volume \(V\) and temperature \(T\) is expanded isothermally to volume \(4V\). Thereafter, the gas is heated isochorically (at constant volume) till its pressure becomes \(P\). If \(R\) is the universal gas constant, the total heat transfer in the process, in units of \(RT\) is _________ .
(Round off to 2 decimal places)
Check Answer
Ans 5.88-5.94
Q.No:48 JAM-2021
The rms velocity of molecules of oxygen gas is given by \(v\) at some temperature \(T\). The molecules of another gas have the same rms velocity at temperature \(\frac{T}{16}\). The second gas is
(A)
Hydrogen
(B)
Helium
(C)
Nitrogen
(D)
Neon
Check Answer
Option A
Q.No:49 JAM-2021
A system undergoes a thermodynamic transformation from state \(S_1\) to state \(S_2\) via two different paths 1 and 2. The heat absorbed and work done along path 1 are 50 J and 30 J, respectively. If the heat absorbed along path 2 is 30 J, the work done along path 2 is
(A)
Zero
(B)
\(10\) J
(C)
\(20\) J
(D)
\(30\) J
Check Answer
Option B
Q.No:50 JAM-2021
A gaseous system, enclosed in an adiabatic container, is in equilibrium at pressure \(P_1\) and volume \(V_1\). Work is done on the system in a quasi-static manner due to which the pressure and volume change to \(P_2\) and \(V_2\), respectively, in the final equilibrium state. At every instant, the pressure and volume obey the condition \(PV^\gamma=C\), where \(\gamma =\frac{C_P}{C_V}\) and \(C\) is a constant. If the work done is zero, then identify the correct statement(s).
(A)
\(P_2V_2=P_1V_1\)
(B)
\(P_2V_2=\gamma P_1V_1\)
(C)
\(P_2V_2=(\gamma +1)P_1V_1\)
(D)
\(P_2V_2=(\gamma -1)P_1V_1\)
Check Answer
Option A
Q.No:51 JAM-2021
An isolated ideal gas is kept at a pressure \(P_1\) and volume \(V_1\). The gas undergoes free expansion and attains a pressure \(P_2\) and volume \(V_2\). Identify the correct statement(s). (\(\gamma =\frac{C_P}{C_V}\))
(A)
This is an adiabatic process
(B)
\(P_1V_1=P_2V_2\)
(C)
\(P_1V_1^\gamma=P_2V_2^\gamma\)
(D)
This is an isobaric process
Check Answer
Option A,B
Q.No:52 JAM-2021
A Carnot engine operates between two temperatures, \(T_L\)=100 K and \(T_H\)= 150 K. Each cycle of the engine lasts for 0.5 seconds during which the power delivered is 500 J/second. Let \(Q_H\) be the corresponding heat absorbed by the engine and \(Q_L\) be the heat lost. Identify the correct statement(s).
(A)
\(Q_H=750\) J
(B)
\(\frac{Q_H}{Q_L}\leq \frac{2}{3}\)
(C)
The change in entropy of the engine and the hot bath in a cycle is 5 J/K
(D)
The change in entropy of the engine in 0.5 seconds is zero
Check Answer
Option A,C,D
Q.No:53 JAM-2021
Consider \(N_1\) number of ideal gas particles enclosed in a volume \(V_1\). If the volume is changed to \(V_2\) and the number of particles is reduced by half, the mean free path becomes four times of its initial value. The ratio \(\frac{V_1}{V_2}\) is __________________ (Round off to two decimal places).
Check Answer
Ans 0.5
Q.No:54 JAM-2021
At some temperature \(T\), two metals \(A\) and \(B\), have Fermi energies \(\epsilon_A\) and \(\epsilon_B\), respectively.
The free electron density of \(A\) is 64 times that of \(B\). The ratio \(\frac{\epsilon_A}{\epsilon_B}\) is _______________ (Round off to two decimal places).
Check Answer
Ans 16
Q.No:55 JAM-2022
Consider a classical ideal gas of \(N\) molecules in equilibrium at temperature \(T\). Each molecule has two energy levels,\(-\epsilon\) and \(\epsilon\). The mean energy of the gas is
(A)
0
(B)
\(N\epsilon \hspace{0.5mm} tanh(\frac{\epsilon}{k_B T})\)
(C)
\(-N\epsilon \hspace{0.5mm} tanh(\frac{\epsilon}{k_B T})\)
(D)
\(\frac{\epsilon}{2}\)
Check Answer
Option C
Q.No:56 JAM-2022
At a temperature \(T\), let \(\beta\) and \(\kappa\) denote the volume expansivity and isothermal compressibility of a gas, respectively. Then \(\frac{\beta}{\kappa}\) is equal to
(A)
\((\frac{\partial P}{\partial T})_V\)
(B)
\((\frac{\partial P}{\partial V})_T\)
(C)
\((\frac{\partial T}{\partial P})_V\)
(D)
\((\frac{\partial T}{\partial V})_P\)
Check Answer
Option A
Q.No:57 JAM-2022
An ideal gas in equilibrium at temperature \(T\) expands isothermally to twice its initial volume. If \(\Delta S, \Delta U\) and \(\Delta F\) denote the changes in its entropy, internal energy and Helmholtz free energy respectively, then
(A)
\(\Delta S 0 , \Delta F <0\)
(B)
\(\Delta S >0 , \Delta U =0 , \Delta F <0\)
(C)
\(\Delta S0\)
(D)
\(\Delta S >0 , \Delta U >0 , \Delta F =0\)
Check Answer
Option B
Q.No:58 JAM-2022
For a certain thermodynamic system, the internal energy \(U=PV\) and \(P\) is proportional to \(T^2\). The entropy of the system is proportional to
(A)
\(UV\)
(B)
\(\sqrt{\frac{U}{V}}\)
(C)
\(\sqrt{\frac{V}{U}}\)
(D)
\(\sqrt{UV}\)
Check Answer
Option D
Q.No:59 JAM-2022
The figure shows a section of the phase boundary separating the vapour (1) and liquid (2) states of water in the P-T plane. Here, C is the critical point. \(\mu_1 , v_1\) and \(s_1\) are the chemical potential, specific volume and specific entropy of the vapour phase respectively, while \(\mu_2 , v_2\) and \(s_2\) respectively denote the same for
the liquid phase. Then
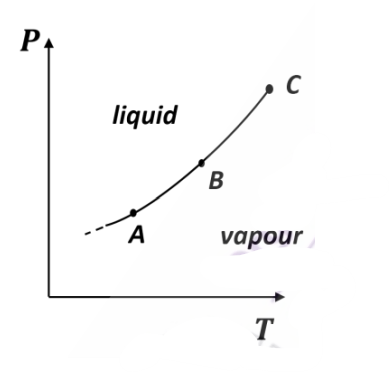
(A)
\(\mu_1=\mu_2\) along AB
(B )
\(v_1=v_2\) along AB
(C)
\(s_1=s_2\) along AB
(D)
\(v_1=v_2\) at the point C
Check Answer
Option A,D
Q.No:60 JAM-2022
For an ideal gas, AB and CD are two isothermals at temperatures \(T_1\) and \(T_2(T_1 > T_2)\) , respectively. AD and BC represent two adiabatic paths as shown in figure. Let \(V_A, V_B ,V_C\) and \(V_D\) be the volumes of the gas at A, B, C and D respectively. If \(\frac{V_C}{V_B}=2\), then \(\frac{V_D}{V_A=}\) _________________.
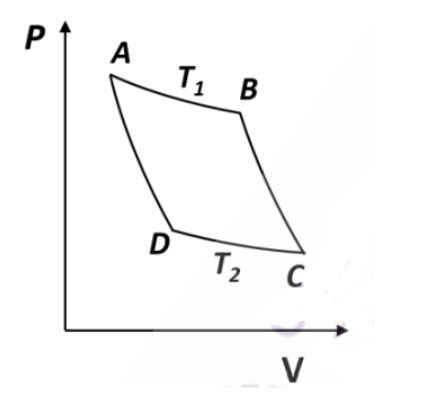
Check Answer
Ans 2
Q.No:61 JAM-2022
A box contains a mixture of two different ideal monoatomic gases, 1 and 2, in equilibrium at temperature \(T\). Both gases are present in equal proportions. The atomic mass for gas 1 is m, while the same for gas 2 is 2m. If the rms speed of a gas molecule selected at random is \(v_{rms}=x\sqrt{\frac{k_B T}{m}}\), then \(x\) is ______________ (Round off to 2 decimal places).
Check Answer
Ans 1.50 OR 1.57
Q.No:62 JAM-2022
A hot body with constant heat capacity 800 J/K at temperature 925 K is dropped gently into a vessel containing 1 kg of water at temperature 300 K and the combined system is allowed to reach equilibrium. The change in the total entropy \(\Delta S\) is ____________________ \(\frac{J}{k}\) (Round off to 1 decimal place).
[Take the specific heat capacity of water to be 4200 J/kg K. Neglect any loss of heat to the vessel and air and change in the volume of water.]
Check Answer
Ans 537.5-537.7 OR 549.8-550.2
Q.No:63 JAM-2018
Which one of the figures correctly represents the T-S diagram of a Carnot engine?
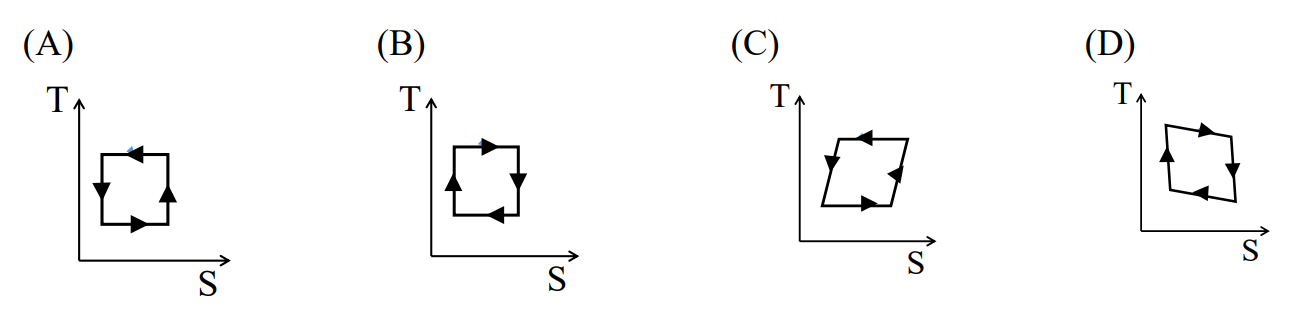
Check Answer
Option B
Q.No:64 JAM-2018
For a metal, the electron density is \(6.4\times 10^{28}m^{-3}\). The Fermi energy is _______________________ eV.
(\(h=6.626\times 10^{-34}\)J s, \(m_e=9.11\times 10^{-31}\)kg, \(1eV=1.6\times 10^{-19}\) J)
(Specify your answer in electron volts (eV) upto one digit after the decimal point.)
Check Answer
Ans 5.6-6.0
Q.No:65 JAM-2023
Which of the following statements about the viscosity of a dilute ideal gas is correct?
A) It is independent of pressure at fixed temperature
B) It increases with increasing pressure at fixed temperature
C) It is independent of temperature
D) It decreases with increasing temperature
Check Answer
Option A
Q.No:66 JAM-2023
A system has \(N\) spins, where each spin is capable of existing in 4 possible states. The difference in entropy of disordered states (where all possible spin configurations are equally probable) and ordered states is
A) \(2(N-1) k_B \hspace{0.5mm} ln2\)
B) \((N-1) k_B \hspace{0.5mm} ln2\)
C) \(4 k_B \hspace{0.5mm} lnN\)
D) \(N k_B \hspace{0.5mm} ln2\)
Check Answer
Option A
Q.No:67 JAM-2023
Temperature (\(T\)) dependence of the total specific heat (\(C_V\)) for a two dimensional metallic solid at low temperatures is
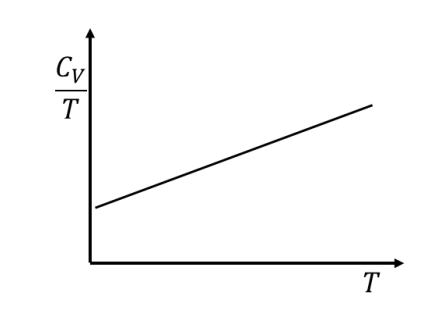

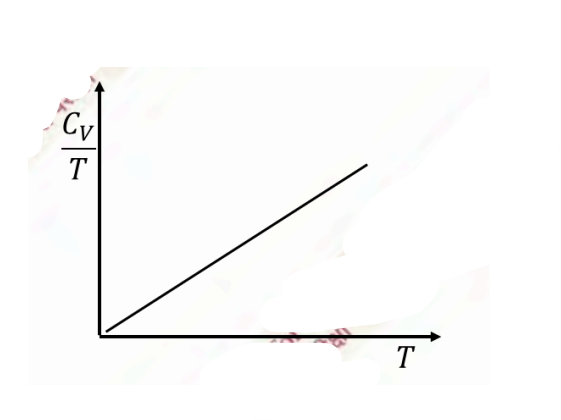
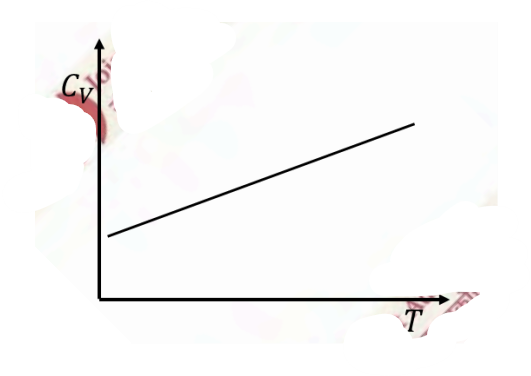
Check Answer
Option A
Q.No:68 JAM-2023
For a thermodynamic system, the coefficient of volume expansion
\(\beta= \frac{1}{V} (\frac{\partial V}{\partial T})_P\)
and compressibility \(\kappa= -\frac{1}{V} (\frac{\partial V}{\partial P})_T\), where \(V, T\) and \(P\) are respectively the volume, temperature, and pressure. Considering that \(\frac{d V}{V}\)
is a perfect differential, we get
A) \((\frac{\partial \beta}{\partial P})_T=(\frac{\partial \kappa}{\partial T})_P\)
B) \((\frac{\partial \beta}{\partial T})_P=-(\frac{\partial \kappa}{\partial P})_T\)
C) \((\frac{\partial \beta}{\partial P})_T=-(\frac{\partial \kappa}{\partial T})_P\)
D) \((\frac{\partial \beta}{\partial T})_P=(\frac{\partial \kappa}{\partial P})_T\)
Check Answer
Option C
Q.No:69 JAM-2023
For the Maxwell-Boltzmann speed distribution, the ratio of the root-mean-square speed (\(v_{rms}\)) and the most probable speed (\(v_{max}\)) is
Given: Maxwell-Boltzmann speed distribution function for a collection of particles of mass \(m\) is
\[f(v)=(\frac{m}{2\pi k_B T})^{3/2} \hspace{1mm} 4\pi v^2 \hspace{1mm} exp(-\frac{mv^2}{2k_B T})\]
A) \(\sqrt{\frac{3}{2}}\)
B) \(\sqrt{\frac{2}{3}}\)
C) \(\frac{3}{2}\)
D) \(\frac{2}{3}\)
Check Answer
Option A
Q.No:70 JAM-2023
Consider a system of large number of particles that can be in three energy states with energies 0 meV, 1 meV, and 2 meV. At temperature \(T\)= 300 K, the mean energy of the system (in meV) is closest to
Given: Boltzmann constant \(k_B\) = 0.086 meV\(K^{-1}\)
A) 0.12
B) 0.97
C)1.32
D) 1.82
Check Answer
Option B
Q.No:71 JAM-2023
A container is occupied by a fixed number of non-interacting particles. If they are obeying Fermi-Dirac, Bose-Einstein, and Maxwell-Boltzmann statistics, the pressure in the container is \(P_{FD}, P_{BE}\) and \(P_{MB}\), respectively. Then
A) \(P_{FD}>P_{MB}>P_{BE}\)
B) \(P_{FD}>P_{MB}=P_{BE}\)
C) \(P_{FD}>P_{BE}>P_{MB}\)
D) \(P_{FD}=P_{MB}=P_{BE}\)
Check Answer
Option A
Q.No:72 JAM-2023
Which of the following schematic plots correctly represent(s) a first order phase transition occurring at temperature \(T=T_c\)? Here \(g,s,v\) are specific Gibbs free energy, entropy and volume, respectively.
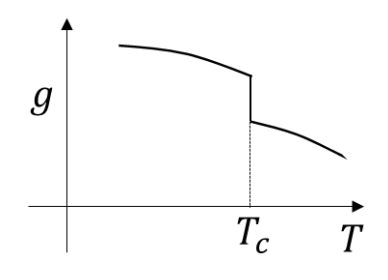

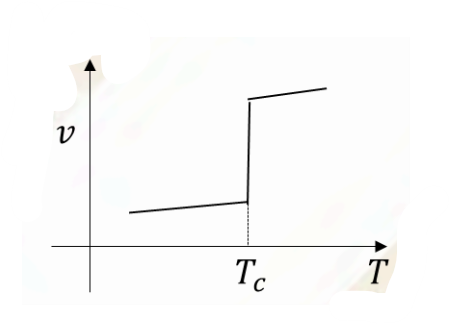
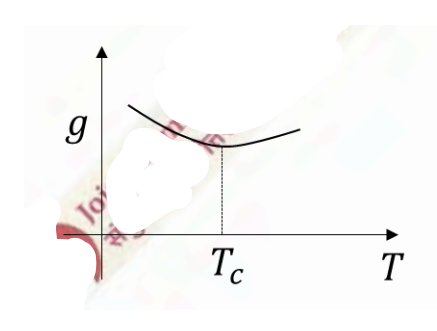
Check Answer
Option B,C
Q.No:73 JAM-2023
A container of volume \(V\) has helium gas in it with \(N\) number of He atoms. The mean free path of these atoms is \(\lambda_{He}\). Another container has argon gas with the same number of Ar atoms in volume \(2V\) with their mean free path being \(\lambda_{Ar}\). Taking the radius of \(Ar\) atoms to be 1.5 times the radius of He atoms, the ratio
\(\lambda_{Ar}/\lambda_{He}\) is ________________________(rounded off to two decimal places).
Check Answer
Ans 0.85-0.95
Q.No:74 JAM-2024
A cylinder-piston system contains \( N \) atoms of an ideal gas. If \( t_{\text{avg}} \) is the average time between successive collisions of a given atom with other atoms. If the temperature \( T \) of the gas is increased isobarically, then \( t_{\text{avg}} \) is proportional to:
A) \( \sqrt{T} \)
B) \( \frac{1}{\sqrt{T}} \)
C) \( T \)
D) \( \frac{1}{T} \)
Check Answer
Option A
Q.No:75 JAM-2024
A gas consists of particles, each having three translational and three rotational degrees of freedom. The ratio of specific heats, \( C_p/C_v \), is:
(\( C_p \) and \( C_v \) are the specific heats at constant pressure and constant volume, respectively)
A) \( \frac{5}{3} \)
B) \( \frac{7}{5} \)
C) \( \frac{4}{3} \)
(D) \( \frac{3}{2} \)
Check Answer
Option C
Q.No:76 JAM-2024
The P-V diagram of an engine is shown in the figure below. The temperatures at points 1, 2, 3 and 4 are \( T_1 \), \( T_2 \), \( T_3 \), and \( T_4 \), respectively. 1 \(\rightarrow\) 2 and 3 \(\rightarrow\) 4 are adiabatic processes, and 2 \(\rightarrow\) 3 and 4 \(\rightarrow\) 1 are isochoric processes.

Identify the correct statement(s).
[\( \gamma \) is the ratio of specific heats \( C_p \) (at constant \( P \)) and \( C_V \) (at constant \( V \))]
A) \( T_1T_3 = T_2T_4 \)
B) The efficiency of the engine is \( 1 - \left(\frac{P_1}{P_2}\right)^{\frac{{\gamma-1}}{\gamma}}\)
C) The change in entropy for the entire cycle is zero
D) \( T_1T_2 = T_3T_4 \)
Check Answer
Option MTA
Q.No:77 JAM-2024
One mole of an ideal monatomic gas, initially at temperature \( T_0 \), is expanded from an initial volume \( V_0 \) to \( 2.5V_0 \). Which of the following statements is(are) correct?
(\( R \) is the ideal gas constant)
A) When the process is isothermal, the work done is \( RT_0 \ln 2 \)
B) When the process is isothermal, the change in internal energy is zero
C) When the process is isobaric, the work done is \( \frac{3}{2} RT_0 \)
D) When the process is isobaric, the change in internal energy is \( \frac{9}{2} RT_0 \)
Check Answer
Option B,C
Q.No:78 JAM-2024
The Fermi energy of a system is \( 5.5eV \). At \( 500K \), the energy of a level for which the probability of occupancy is \( 0.2 \), is _________eV. (Rounded off to two decimal places)
(Boltzmann constant \( k_B = 8.62 \times 10^{-5} eV/K \))
Check Answer
Ans 5.55-5.57
Q.No:79 JAM-2024
One mole of an ideal monatomic gas is heated in a closed container, first from \( 273K \) to \( 303K \), and then from \( 303K \) to \( 373K \). The net change in the entropy is ______________ \( R \). (Rounded off to two decimal places)
Check Answer
Ans 0.44-0.48
Q.No:80 JAM-2025
Consider Maxwell’s relation
\[
\left(\frac{\partial S}{\partial V}\right)_T
=
\left(\frac{\partial P}{\partial T}\right)_V .
\]
The equation of state of a thermodynamic system is given as
\[
P = \frac{A T}{V^2} + \frac{B T^3}{V},
\]
where \(A\) and \(B\) are constants of appropriate dimensions.
Then \(\left(\frac{\partial C_V}{\partial V}\right)_T\) of the system varies with
temperature as
(\(C_V\) is the heat capacity at constant volume)
A) \(T^2\)
B) \(T\)
C) \(T^{-1}\)
D) \(T^3\)
Check Answer
Option A
Q.No:81 JAM-2025
Three gaseous systems, \(G_1, G_2,\) and \(G_3\) with pressure and volume
\((P_1, V_1), (P_2, V_2),\) and \((P_3, V_3)\), respectively, are such that
(I) when \(G_1\) and \(G_2\) are in thermal equilibrium,
\[
P_1 V_1 - P_2 V_2 + \alpha P_2 = 0
\]
is satisfied, and
(II) when \(G_1\) and \(G_3\) are in thermal equilibrium,
\[
P_3 V_3 - P_1 V_1 + \frac{\beta P_1 V_1}{V_3} = 0
\]
is satisfied.
The relation(s) valid at thermal equilibrium is(are)
(\(\alpha\) and \(\beta\) are constants of appropriate dimensions)
A) \(
P_3 V_3 - (P_2 V_2 - \alpha P_2)\left(1 - \frac{\beta}{V_3}\right) = 0
\)
B) \(
P_3 V_3 + (P_2 V_2 + \alpha P_2)\left(1 + \frac{\beta}{V_3}\right) = 0
\)
C) \(
P_1 V_1 = P_2 V_2 = P_3 V_3
\)
D) \(
P_3 V_3 + P_1 V_1\left(\frac{\beta}{V_3} - 1\right) = 0
\)
Check Answer
Option A,D
Q.No:82 JAM-2025
An ideal mono-atomic gas is expanded adiabatically from A to B.
It is then compressed in an isobaric process from B to C.
Finally, the pressure is increased in an isochoric process from C to A.
The cyclic process is shown in the figure.
For this system, which of the following is(are) correct?
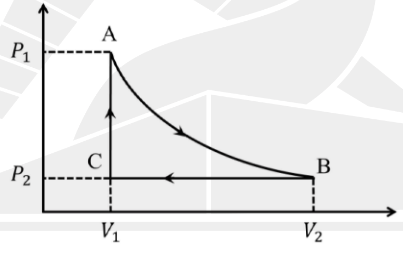
A) Work done along the path AB is \((P_1V_1 - P_2V_2)\)
B) Total work done during the entire process is
\(
\frac{3}{2}(P_1V_1 - P_2V_2) + P_2(V_1 - V_2)
\)
C) Total heat absorbed during the entire process is
\(
\frac{3}{2}(P_1 - P_2)V_1
\)
D) Total change in internal energy during the entire process is
\(
\frac{5}{2}P_2(V_2 - V_1)
\)
Check Answer
Option B
Q.No:83 JAM-2025
G1 and G2 are two ideal gases at temperatures \(T_1\) and \(T_2\), respectively.
The molecular weight of the constituents of G1 is half that of G2.
If the average speeds of the molecules of both gases are equal, then assuming
Maxwell–Boltzmann distributions for the molecular speeds, the ratio
\(\frac{T_2}{T_1}\) is _____ (in integer).
Check Answer
ANS 2
Q.No:84 JAM-2025
In a two-level atomic system, the excited state is 0.2 eV above the ground state.
Considering the Maxwell–Boltzmann distribution, the temperature at which 2% of
the atoms will be in the excited state is _____ K.
(up to two decimal places)
(Boltzmann constant \(k_B = 8.62 \times 10^{-5}\,\text{eV/K}\))
Check Answer
ANS 591 to 597
Q.No:85 JAM-2025
One kg of water at 27°C is brought in contact with a heat reservoir kept at 37°C.
Upon reaching thermal equilibrium, this mass of water is brought in contact with
another heat reservoir kept at 47°C. The final temperature of water is 47°C.
The change in entropy of the whole system in this entire process is _____ cal/K.
(up to two decimal places)
[Take specific heat of water at constant pressure as 1 cal/(g·K)]
Check Answer
ANS 0.9 to 1.1
Q.No:86 JAM-2025
Consider a chamber at room temperature (27 °C) filled with a gas having a
molecular diameter of 0.35 nm. The pressure (in Pascal) to which the chamber
needs to be evacuated so that the molecules have a mean free path of 1 km is
_____ × \(10^{-5}\)Pa. (up to two decimal places)
(Boltzmann constant \(k_B\) = 1.38 × \(10^{-23}\) J/K)
