Q.No:1 GATE-2012
The isothermal compressibility, \(\kappa\) of an ideal gas at temperature \(T_0\) and volume \(V_0\), is given by
(A)
\(-\frac{1}{V_0} \left.\frac{\partial V}{\partial P}\right|_{T_0}\)
(B)
\(\frac{1}{V_0} \left.\frac{\partial V}{\partial P}\right|_{T_0}\)
(C)
\(-V_0 \left.\frac{\partial P}{\partial V}\right|_{T_0}\)
(D)
\(V_0 \left.\frac{\partial P}{\partial V}\right|_{T_0}\)
Check Answer
Option A
Q.No:2 GATE-2013
Across a first order phase transition, the free energy is
(A)
proportional to the temperature
(B)
a discontinuous function of the temperature
(C)
a continuous function of the temperature but its first derivative is discontinuous
(D)
such that the first derivative with respect to temperature is continuous
Check Answer
Option B
Q.No:3 GATE-2014
For a gas under isothermal conditions, its pressure \(P\) varies with volume \(V\) as \(P\propto V^{-5/3}\). The bulk modulus \(B\) is proportional to
(A)
\(V^{-1/2}\)
(B)
\(V^{-2/3}\)
(C)
\(V^{-3/5}\)
(D)
\(V^{-5/3}\)
Check Answer
Option D
Q.No:4 GATE-2016
For a system at constant temperature and volume, which of the following statements is correct at equilibrium?
(A)
The Helmholtz free energy attains a local minimum.
(B)
The Helmholtz free energy attains a local maximum.
(C)
The Gibbs free energy attains a local minimum.
(D)
The Gibbs free energy attains a local maximum.
Check Answer
Option A
Q.No:5 GATE-2017
A reversible Carnot engine is operated between temperatures \(T_1\) and \(T_2\) (\(T_2>T_1\)) with a photon gas as the working substance. The efficiency of the engine is
(A)
\(1-\frac{3T_1}{4T_2}\)
(B)
\(1-\frac{T_1}{T_2}\)
(C)
\(1-\left(\frac{T_1}{T_2})\right)^{3/4}\)
(D)
\(1-\left(\frac{T_1}{T_2})\right)^{4/3}\)
Check Answer
Option B
Q.No:6 GATE-2017
Water freezes at \(0^{\circ}C\) at atmospheric pressure (\(1.01\times 10^5 Pa\)). The densities of water and ice at this temperature and pressure are \(1000 kg/m^3\) and \(934 kg/m^3\) respectively. The latent heat of fusion is \(3.34\times 10^5 J/kg\). The pressure required for depressing the melting temperature of ice by \(10^{\circ}C\) is __________ GPa. (up to two decimal places)
Check Answer
Ans 0.15-0.19
Q.No:7 GATE-2018
An air-conditioner maintains the room temperature at \(27^{\circ}C\) while the outside temperature is \(47^{\circ}C\). The heat conducted through the walls of the room from outside to inside due to temperature difference is \(7000 W\). The minimum work done by the compressor of the air-conditioner per unit time is _____________ W.
Check Answer
Ans 466-467
Q.No:8 GATE-2019
In a thermally insulated container, \(0.01 kg\) of ice at \(273 K\) is mixed with \(0.1 kg\) of water at \(300 K\). Neglecting the specific heat of the container, the change in the entropy of the system in \(J/K\) on attaining thermal equilibrium (rounded off to two decimal places) is ____________
(Specific heat of water is \(4.2 kJ/kg-K\) and the latent heat of ice is \(335 kJ/kg\)).
Check Answer
Ans 1.02-1.04
Q.No:9 GATE-2020
As shown in the figure, an ideal gas is confined to chamber A of an insulated container, with vacuum in chamber B. When the plug in the wall separating the chambers A and B is removed, the gas fills both the chambers. Which one of the following statements is true?

(A) The temperature of the gas remains unchanged
(B)
Internal energy of the gas decreases
(C)
Temperature of the gas decreases as it expands to fill the space in chamber B
(D)
Internal energy of the gas increases as its atoms have more space to move around
Check Answer
Option A
Q.No:10 GATE-2020
The internal energy \(U\) of a system is given by \(U(S, V)=\lambda V^{-2/3} S^2\), where \(\lambda\) is a constant of appropriate dimensions; \(V\) and \(S\) denote the volume and entropy, respectively. Which one of the following gives the correct equation of state of the system?
(A)
\(\frac{PV^{1/3}}{T^{2}}=\text{constant}\)
(B)
\(\frac{PV}{T^{1/3}}=\text{constant}\)
(C)
\(\frac{P}{V^{1/3}T}=\text{constant}\)
(D)
\(\frac{PV^{2/3}}{T}=\text{constant}\)
Check Answer
Option A
Q.No:11 GATE-2022
Which of the following relationship between the internal energy \(U\) and the Helmholtz's free energy \(F\) is true?
(a)
\(U=-T^2\left[\frac{\partial \left(\frac{F}{T}\right)}{\partial T}\right]_V\)
(b)
\(U=+T^2\left[\frac{\partial \left(\frac{F}{T}\right)}{\partial T}\right]_V\)
(c)
\(U=+T\left[\frac{\partial F}{\partial T}\right]_V\)
(d)
\(U=-T\left[\frac{\partial F}{\partial T}\right]_V\)
Check Answer
Option a
Q.No:12 GATE-2022
Water at \(300 \hspace{1mm}\text{K}\) can be brought to \(320 \hspace{1mm}\text{K}\) using one of the following processes.
Process 1: Water is brought in equilibrium with a reservoir at \(320 \hspace{1mm}\text{K}\) directly.
Process 2: Water is first brought in equilibrium with a reservoir at \(310 \hspace{1mm}\text{K}\) and then with the reservoir at \(320 \hspace{1mm}\text{K}\).
Process 3: Water is first brought in equilibrium with a reservoir at \(350 \hspace{1mm}\text{K}\) and then with the reservoir at \(320 \hspace{1mm}\text{K}\).
The corresponding changes in the entropy of the universe for these processes are \(\Delta S_1, \Delta S_2\) and \(\Delta S_3\), respectively. Then
(a)
\(\Delta S_2>\Delta S_1>\Delta S_3\)
(b)
\(\Delta S_3>\Delta S_1>\Delta S_2\)
(c)
\(\Delta S_3>\Delta S_2>\Delta S_1\)
(d)
\(\Delta S_1>\Delta S_2>\Delta S_3\)
Check Answer
Option b
Q.No:13 GATE-2022
A piston of mass \(m\) is fitted to an airtight horizontal cylindrical jar. The cylinder and piston have identical unit area of cross-section. The gas inside the jar has volume \(V\) and is held at pressure \(P=P_{\text{atmosphere}}\). The piston is pushed inside the jar very slowly over a small distance. On releasing, the piston performs an undamped simple harmonic motion of low frequency. Assuming that the gas is ideal and no heat is exchanged with the atmosphere, the frequency of the small oscillations is proportional to
(a)
\(\sqrt{\frac{P}{\gamma mV}}\)
(b)
\(\sqrt{\frac{P\gamma}{Vm}}\)
(c)
\(\sqrt{\frac{P}{mV\gamma^{-1}}}\)
(d)
\(\sqrt{\frac{\gamma P}{mV\gamma^{-1}}}\)
Check Answer
Option b
Q.No:14 GATE-2022
A paramagnetic salt of mass \(m\) is held at temperature \(T\) in a magnetic field \(H\). If \(S\) is the entropy of the salt and \(M\) is its magnetization, then \(dG=-SdT-MdH\), where \(G\) is the Gibbs free energy. If the magnetic field is changed adiabatically by \(\Delta H\to 0\) and the corresponding infinitesimal changes in entropy and temperature are \(\Delta S\) and \(\Delta T\), then which of the following statements are correct
(a)
\(\Delta S=-\frac{1}{T}\left(\frac{\partial G}{\partial T}\right)_H \Delta T\)
(b)
\(\Delta S=0\)
(c)
\(\Delta T=-\frac{\left(\frac{\partial M}{\partial T}\right)_H}{\left(\frac{\partial S}{\partial T}\right)_H}\Delta H\)
(d)
\(\Delta T=0\)
Check Answer
Option b,c
Q.No:15 GATE-2023
Which one of the following entropy (S) - temperature (T) diagrams CORRECTLY represents the Carnot cycle \(abcda\) shown in the P-V diagram?
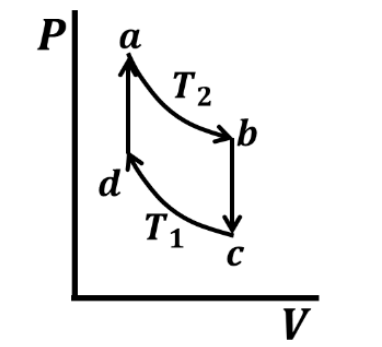
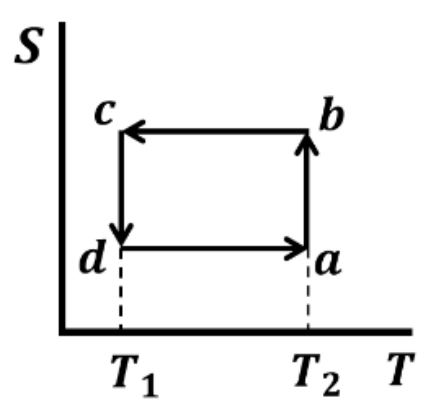
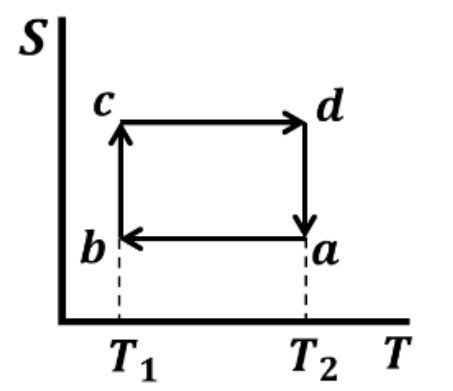


Check Answer
Option A
Q.No:16 GATE-2023
Which of the following is(are) the CORRECT option(s) for the Joule-Thomson effect?
(A)
It is an isentropic process
(B)
It is an isenthalpic process
(C)
It can result in cooling as well as heating
(D)
For an ideal gas it always results in cooling
Check Answer
Option B, C
Q.No:17 GATE-2023
Two identical bodies kept at temperatures 800 K and 200 K act as the hot and the cold reservoirs of an ideal heat engine, respectively. Assume that their heat capacity (\(C\)) in Joules/K is independent of temperature and that they do not undergo any phase change. Then, the maximum work that can be obtained from the heat engine is \(n \times C\) Joules. What is the value of \(n\) (in integer)?
Check Answer
Ans 200
Q.No:18 GATE-2024
If a thermodynamical system is adiabatically isolated and experiences a change in volume under an externally applied constant pressure, then the thermodynamical potential minimized at equilibrium is the
(A) enthalpy
(B) Helmholtz free energy
(C) Gibbs free energy
(D) grand potential
Check Answer
Option A
Q.No:19 GATE-2024
The vapor pressure (\( P \)) of solid ammonia is given by \( \ln(P) = 23.03 - \frac{3754}{T} \), while that of liquid ammonia is given by \( \ln(P) = 19.49 - \frac{3063}{T} \), where \( T \) is the temperature in K.
The temperature of the triple point of ammonia is ______ K (rounded off to two decimal places).
Check Answer
Ans 195.10 to 195.30
Q.No:20 GATE-2025
The Joule–Thomson expansion of a gas is
A) Isentropic
B) Isenthalpic
C) Isobaric
D) Isochoric
Check Answer
Option B
Q.No:21 GATE-2025
A schematic Pressure–Temperature diagram of water is shown in the figure.
Which of the following option(s) is/are correct?

A) Clausius–Clapeyron equation is valid across the melting curve and the vaporization curve
B) Melting curve has the highest slope
C) The critical point exists only for the vaporization curve
D) Clausius–Clapeyron equation is not valid across the melting curve and the vaporization curve
Check Answer
Options A,B,C
Q.No:22 GATE-2025
One mole of an ideal monatomic gas at absolute temperature \(T\) undergoes free expansion
to double its original volume, so that the entropy change is \(\Delta S_1\).
An identical amount of the same gas at absolute temperature \(2T\) undergoes isothermal
expansion to double its original volume, so that the entropy change is \(\Delta S_2\).
The value of \(\frac{\Delta S_1}{\Delta S_2}\) (in integer) is ______
Check Answer
Ans 1
Q.No:1 CSIR Dec-2014
Two solid iron spheres are heated to \(100^{\circ}C\) and then allowed to cool. One has the size of a football; the other has the size of a pea. Which sphere will attain the room temperature (constant) first?
(1)
The bigger sphere
(2)
The smaller sphere
(3)
Both spheres will take the same time
(4)
It will depend on the room temperature
Check Answer
Option 2
Q.No:2 CSIR Dec-2014
When a gas expands adiabatically from volume \(V_1\) to \(V_2\) by a quasi-static reversible process, it cools from temperature \(T_1\) to \(T_2\). If now the same process is carried out adiabatically and irreversibly, and \(T_2'\) is the temperature of the gas when it has equilibrated, then
(1)
\(T_2'=T_2\)
(2)
\(T_2'>T_2\)
(3)
\(T_2'=T_2\left(\frac{V_2-V_1}{V_2}\right)\)
(4)
\(T_2'=\frac{T_2 V_1}{V_2}\)
Check Answer
Option 2
Q.No:3 CSIR June-2015
The condition for the liquid and vapour phases of a Ouid to be in equilibrium is given by the approximate equation \(\frac{dP}{dT}=frac{Q_1}{Tv_{vap}}\) (Clausius-Clayperon equation),
where \(V_{vap}\) is the volume per particle in the vapour phase, and \(Q_1\) is the latent heat, which may be taken to be a constant. If the vapour obeys ideal gas law, which of the following plots is correct?
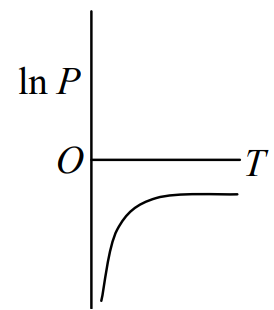



Check Answer
Option 1 & 3
Q.No:4 CSIR June-2015
A large number \(N\) of Brownian particles in one dimension start their diffusive motion from the origin at time \(t= 0\). The diffusion coefficient is \(D\). The number of particles crossing a point at a distance \(L\) from the origin, per unit time, depends on \(L\) and time \(t\) as
(1)
\(\frac{N}{\sqrt{4 \pi D t}} e^{-L^{2} /(4 D t)}\)
(2)
\(\frac{N L}{\sqrt{4 \pi D t}} e^{-4 D t / L^{2}}\)
(3)
\(\frac{N}{\sqrt{16 \pi D t^{3}}} e^{-L^{2} /(4 D t)}\)
(4)
\(N e^{-4 D t / L^{2}}\)
Check Answer
Option
Q.No:5 CSIR Dec-2015
The heat capacity of (the interior of) a refrigerator is \(4.2 \text{ kJ/K}\). The minimum work that must be done to lower the internal temperature from \(18^{\circ} \text{C}\) to \(17^{\circ} \text{C}\) when the outside temperature is \(27^{\circ} \text{C}\) is
(1)
\(2.20 \text{ kJ}\)
(2)
\(0.80 \text{ kJ}\)
(3)
\(0.30 \text{ kJ}\)
(4)
\(0.14 \text{ kJ}\)
Check Answer
Option 4
Q.No:6 CSIR June-2016
When an ideal monatomic gas is expanded adiabatically from an initial volume \(V_0\) to \(3V_0\), its temperature changes from \(T_0\) to \(T\). Then the ratio \(T/T_0\) is
(1)
\(\frac{1}{3}\)
(2)
\(\left(\frac{1}{3}\right)^{2/3}\)
(3)
\(\left(\frac{1}{3}\right)^{1/3}\)
(4)
\(3\)
Check Answer
Option 2
Q.No:7 CSIR June-2016
A box of volume \(V\) containing \(N\) molecules of an ideal gas, is divided by a wall with a hole into two compartments. If the volume of the smaller compartment is \(V/3\), the variance of the number of particles in it, is
(1)
\(N/3\)
(2)
\(2N/9\)
(3)
\(\sqrt{N}\)
(4)
\(\sqrt{N}/3\)
Check Answer
Option 2
Q.No:8 CSIR Dec-2016
A silica particle of radius \(0.1 \mu m\) is put in a container of water at \(T=300 K\). The densities of silica and water are \(2000 kg/m^3\) and \(1000 kg/m^3\), respectively. Due to thermal fluctuations, the particle is not always at the bottom of the container. The average height of the particle above the base of the container is approximately
(1)
\(10^{-3} m\)
(2)
\(3\times 10^{-4} m\)
(3)
\(10^{-4} m\)
(4)
\(5\times 10^{-5} m\)
Check Answer
Option 3
Q.No:9 CSIR June-2017
A thermodynamic function
\[
G(T, P, N)=U-TS+PV
\]
is given in terms of the internal energy \(U\), temperature \(T\), entropy \(S\), pressure \(P\), volume \(V\) and the number of particles \(N\). Which of the following relations is true? (In the following \(\mu\) is the chemical potential.)
(1)
\(S=\left.-\frac{\partial G}{\partial T}\right|_{N, P}\)
(2)
\(S=\left.\frac{\partial G}{\partial T}\right|_{N, P}\)
(3)
\(V=\left.-\frac{\partial G}{\partial P}\right|_{N, T}\)
(4)
\(\mu=\left.-\frac{\partial G}{\partial N}\right|_{P, T}\)
Check Answer
Option 1
Q.No:10 CSIR June-2017
A box, separated by a movable wall, has two compartments filled by a monoatomic gas of \(\frac{C_P}{C_V}=\gamma\). Initially the volumes of the two compartments are equal, but the pressures are \(3P_0\) and \(P_0\), respectively. When the wall is allowed to move, the final pressures in the two compartments become equal. The final pressure is
(1)
\(\left(\frac{2}{3}\right)^{\gamma} P_0\)
(2)
\(3\left(\frac{2}{3}\right)^{\gamma} P_0\)
(3)
\(\frac{1}{2}(1+3^{1/\gamma})^{\gamma} P_0\)
(4)
\(\left(\frac{3^{1/\gamma}}{1+3^{1/\gamma}}\right)^{\gamma} P_0\)
Check Answer
Option
Q.No:11 CSIR Dec-2017
A monoatomic gas of volume \(V\) is in equilibrium in a uniform vertical cylinder, the lower end of which is closed by a rigid wall and the other by a frictionless piston. The piston is pressed lightly and released. Assume that the gas is a poor conductor of heat and the cylinder and piston are perfectly insulating. If the cross-sectional area of the cylinder is \(A\), the angular frequency of small oscillations of the piston about the point of equilibrium, is
(1)
\(\sqrt{5gA/(3V)}\)
(2)
\(\sqrt{4gA/(3V)}\)
(3)
\(\frac{5}{3}\sqrt{gA/V}\)
(4)
\(\sqrt{7gA/(5V)}\)
Check Answer
Option 1
Q.No:12 CSIR Dec-2017
The relation between the internal energy \(U\), entropy \(S\), temperature \(T\), pressure \(p\), volume \(V\), chemical potential \(\mu\) and number of particles \(N\) of a thermodynamic system is \(dU=TdS-pdV+\mu dN\). That \(U\) is an exact differential implies that
(1)
\(\left.-\frac{\partial p}{\partial S}\right|_{V, N}=\left.\frac{\partial T}{\partial V}\right|_{S, N}\)
(2)
\(p\left.\frac{\partial U}{\partial T}\right|_{S, N}=S\left.\frac{\partial U}{\partial V}\right|_{S, \mu}\)
(3)
\(p\left.\frac{\partial U}{\partial T}\right|_{S, N}=-\frac{1}{T}\left.\frac{\partial U}{\partial V}\right|_{S, \mu}\)
(4)
\(\left.\frac{\partial p}{\partial S}\right|_{V, N}=\left.\frac{\partial T}{\partial V}\right|_{S, N}\)
Check Answer
Option 1
Q.No:13 CSIR Dec-2017
The number of microstates of a gas of \(N\) particles in a volume \(V\) and of internal energy \(U\), is given by
\[
\Omega(U, V, N)=(V-Nb)^N \left(\frac{aU}{N}\right)^{3N/2},
\]
(where \(a\) and \(b\) are positive constants). Its pressure \(P\), volume \(V\) and temperature \(T\), are related by
(1)
\(\left(P+\frac{aN}{V}\right)(V-Nb)=Nk_B T\)
(2)
\(\left(P-\frac{aN}{V^2}\right)(V-Nb)=Nk_B T\)
(3)
\(PV=Nk_B T\)
(4)
\(P(V-Nb)=Nk_B T\)
Check Answer
Option 4
Q.No:14 CSIR June-2018
Which of the following statements concerning the coefficient of volume expansion \(\alpha\) and the isothermal compressibility \(\kappa\) of a solid is true?
(1)
\(\alpha\) and \(\kappa\) are both intensive variables
(2)
\(\alpha\) is an intensive and \(\kappa\) is an extensive variable
(3)
\(\alpha\) is an extensive and \(\kappa\) is an intensive variable
(4)
\(\alpha\) and \(\kappa\) are both extensive variables
Check Answer
Option 1
Q.No:15 CSIR June-2018
The van der Waals equation for one mole of a gas is \(\left(p+\frac{a}{V^2}\right)(V-b)=RT\). The corresponding equation of state for \(n\) moles of this gas at pressure \(p\), volume \(V\) and temperature \(T\), is
(1)
\(\left(p+\frac{an^2}{V^2}\right)(V-nb)=nRT\)
(2)
\(\left(p+\frac{a}{V^2}\right)(V-nb)=nRT\)
(3)
\(\left(p+\frac{an^2}{V^2}\right)(V-nb)=RT\)
(4)
\(\left(p+\frac{a}{V^2}\right)(V-nb)=RT\)
Check Answer
Option 1
Q.No:16 CSIR June-2018
Consider a particle diffusing in a liquid contained in a large box. The diffusion constant of the particle in the liquid is \(1.0\times 10^{-2} cm^2/s\). The minimum time after which the root-mean-squared displacement becomes more than \(6 cm\) is
(1)
\(10 min\)
(2)
\(6 min\)
(3)
\(30 min\)
(4)
\(\sqrt{6} min\)
Check Answer
Option 1 OR 3
Q.No:17 CSIR June-2018
A thermally insulated chamber of dimensions \((L, L, 2L)\) is partitioned in the middle. One side of the chamber is filled with \(n\) moles of an ideal gas at a pressure \(P\) and temperature \(T\), while the other side is empty. At \(t=0\), the partition is removed and the gas is allowed to expand freely. The time to reach equilibrium varies as

(1)
\(n^{1/3} L^{-1} T^{1/2}\)
(2)
\(n^{2/3} L T^{-1/2}\)
(3)
\(n^{0} L T^{-1/2}\)
(4)
\(n L^{-1} T^{1/2}\)
Check Answer
Option 3
Q.No:18 CSIR June-2018
The pressure \(P\) of a system of \(N\) particles contained in a volume \(V\) at a temperature \(T\) is given by \(P=nk_B T-\frac{1}{2}an^2+\frac{1}{6}bn^3\), where \(n\) is the number density and \(a\) and \(b\) are temperature independent constants. If the system exhibits a gas-liquid transition, the critical temperature is
(1)
\(\frac{a}{bk_B}\)
(2)
\(\frac{a}{2b^2 k_B}\)
(3)
\(\frac{a^2}{2bk_B}\)
(4)
\(\frac{a^2}{b^2 k_B}\)
Check Answer
Option 3
Q.No:19 CSIR June-2019
The equation of state of an ideal gas is \(pV=RT\). At very low temperatures, the volume expansion coefficient \(\frac{1}{V}\frac{\partial V}{\partial T}\) at constant pressure
(1)
diverges as \(1/T^2\)
(2)
diverges as \(1/T\)
(3)
vanishes as \(T\)
(4)
is independent of the temperature
Check Answer
Option 2
Q.No:20 CSIR Dec-2019
A mole of gas at initial temperature \(T_i\) comes into contact with a heat reservoir at temperature \(T_f\) and the system is allowed to reach equilibrium at constant volume. If the specific heat of the gas is \(C_V=\alpha T\), where \(\alpha\) is a constant, the total change in entropy is
(1)
\(zero\)
(2)
\(\alpha(T_f-T_i)+\frac{\alpha}{2T_f}(T_f-T_i)^2\)
(3)
\(\alpha(T_f-T_i)\)
(4)
\(\alpha(T_f-T_i)+\frac{\alpha}{2T_f}(T_f^2-T_i^2)\)
Check Answer
Option 4
Q.No:21 CSIR Dec-2019
An ideal Carnot engine extracts \(100 J\) from a heat source and dumps \(40 J\) to a heat sink at \(300 K\). The temperature of the heat source is
(1)
\(600 K\)
(2)
\(700 K\)
(3)
\(750 K\)
(3)
\(650 K\)
Check Answer
Option 3
Q.No:22 CSIR Dec-2019
The pressure \(p\) of a gas depends on the number density \(\rho\) of particles and the temperature \(T\) as \(p=k_B T\rho-B_2 \rho^2+B_3 \rho^3\) where \(B_2\) and \(B_3\) are positive constants. Let \(T_c, \rho_c\) and \(p_c\) denote the critical temperature, critical number density and critical pressure, respectively. The ratio \(\rho_c k_B T_c/\rho_c\) is equal to
(1)
\(1/3\)
(2)
\(3\)
(3)
\(8/3\)
(4)
\(4\)
Check Answer
Option 2
Q.No:23 Assam CSIR Dec-2019
One mole of an ideal gas is taken through the cycle ABC once in the \(pV\)-diagram, as shown in the figure. The segment BC is horizontal, while AB is vertical. The coordinates of A and C are \((V_0, 2p_0)\) and \((2V_0, p_0)\) respectively, and they are joined by an isotherm. The total work done is

(1)
\(p_0 V_0(2\ln{2}-1)\)
(2)
\(p_0 V_0 \ln{2}\)
(3)
\(2p_0 V_0 \ln{2}\)
(4)
\(p_0 V_0(1-\ln{2})\)
Check Answer
Option 1
Q.No:24 Assam CSIR Dec-2019
A material of inhomogeneous thermal conductivity \(\kappa(\vec{r})\) has a uniform density \(\rho\) and heat capacity \(C_V\). The heat equation obeyed by the time-dependent temperature distribution \(T(\vec{r}, t)\), is
(1)
\(\rho C_V \frac{\partial T(\vec{r}, t)}{\partial t}=\vec{\nabla}\cdot \left(\kappa(\vec{r}) \vec{\nabla} T(\vec{r}, t)\right)\)
(2)
\(\rho C_V \frac{\partial T(\vec{r}, t)}{\partial t}=\kappa(\vec{r}) \nabla^2 T(\vec{r}, t) \)
(3)
\(\rho C_V \frac{\partial T(\vec{r}, t)}{\partial t}=\nabla^2(\kappa(\vec{r}) T(\vec{r}, t))\)
(4)
\(\rho C_V \frac{\partial T(\vec{r}, t)}{\partial t}=\left(\vec{\nabla} \kappa(\vec{r})\right)\cdot \left(\vec{\nabla} T(\vec{r}, t)\right)\)
Check Answer
Option 1
Q.No:25 Assam CSIR Dec-2019
Consider raising the temperature of water from \(70^{\circ}C\) to \(130^{\circ}C\) at one atmospheric pressure. Which of the following plots best represents the dependence of density \(\rho\) on the temperature \(T\)?




Check Answer
Option 4
Q.No:26 Assam CSIR Dec-2019
A box of length \(L\) is divided into two parts by a movable wall. Initially the left part of the box contains only \({Kr}\) gas and the right contains only \({He}\) gas, both at the same pressure and temperature. The material of the wall is semi-permeable that allows \({He}\) atoms to pass through, but not \({Kr}\) atoms. Assuming that the gases are ideal, the position of the wall (with respect to the left of the box) after reaching equilibrium, will be at
(1)
\(L/2\)
(2)
\(2L/3\)
(3)
\(3L/4\)
(4)
\(L\)
Check Answer
Option 4
Q.No:27 CSIR June-2020
Two ideal gases in a box are initially separated by a partition. Let \(N_1, V_1\) and \(N_2, V_2\) be the numbers of particles and volume occupied by the two systems. When the partition is removed, the pressure of the mixture at an equilibrium temperature \(T\), is
(a)
\(k_B T\left(\frac{N_1+N_2}{2(V_1+V_2)}\right)\)
(b)
\(k_B T\left(\frac{N_1+N_2}{V_1+V_2}\right)\)
(c)
\(k_B T\left(\frac{N_1}{V_1}+\frac{N_2}{V_2}\right)\)
(d)
\(\frac{1}{2}k_B T\left(\frac{N_1}{V_1}+\frac{N_2}{V_2}\right)\)
Check Answer
Option b
Q.No:28 CSIR Feb-2022
The ratio \(c_p/c_v\) of the specific heats at constant pressure and volume of a monatomic ideal gas in two dimensions is
(1)
\(3/2\)
(2)
\(2\)
(3)
\(5/3\)
(4)
\(5/2\)
Check Answer
Option 2
Q.No:29 CSIR Sep-2022
A thermally isolated container, filled with an ideal gas at temperature \(T\), is divided by a partition, which is clamped initially, as shown in the figure below.
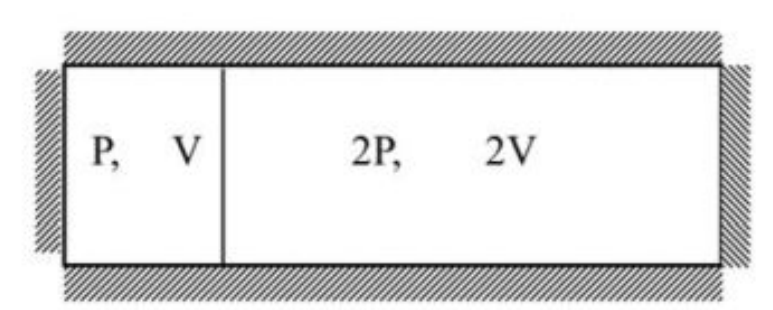
The partition does not allow the gas in the two parts to mix. It is subsequently released and allowed to move freely with negligible friction. The final pressure at equilibrium is
(1)
\(5P/3\)
(2)
\(5P/4\)
(3)
\(3P/5\)
(4)
\(4P/5\)
Check Answer
Option 1
Q.No:30 CSIR Dec-2023
A classical ideal gas is subjected to a reversible process in which its molar specific heat changes with temperature \( T \) as \( C(T) = C_v + \frac{R}{T_0} T \). If the initial temperature and volume are \( T_0 \) and \( V_0 \), respectively, and the final volume is \( 2V_0 \), then the final temperature is
1) \( \frac{T_0}{\ln 2} \)
2) \( 2T_0 \)
3) \( \frac{T_0}{1 - \ln 2} \)
4) \( T_0(1 + \ln 2) \)
Check Answer
Option 4
Q.No:31 CSIR Dec-2023
The work done on a material to change its magnetization \( M \) in an external field \( H \) is \( dW = HdM \). Its Gibbs free energy is
\[
G(T, H) = -\left( \gamma T + \frac{aH^2}{2T} \right),
\]
where \( \gamma, a > 0 \) are constants. The material is in equilibrium at a temperature \( T = T_0 \) and in an external field \( H = H_0 \). If the field is decreased to \( \frac{H_0}{2} \) adiabatically and reversibly, the temperature changes to
1) \(2T_0\)
2) \(\frac{T_0}{2}\)
3) \(\left( \frac{a}{2\gamma} \right)^{\frac{1}{4}} \sqrt{H_0 T_0}\)
4) \( \left( \frac{a}{\gamma} \right)^{\frac{1}{4}} \sqrt{H_0 T_0} \)
Check Answer
Option 2
Q.No:32 CSIR June-2024
The following \(P-V\) diagram shows a process, where an ideal gas is taken quasi-statically from \(A\) to \(B\) along the path as shown in the figure.
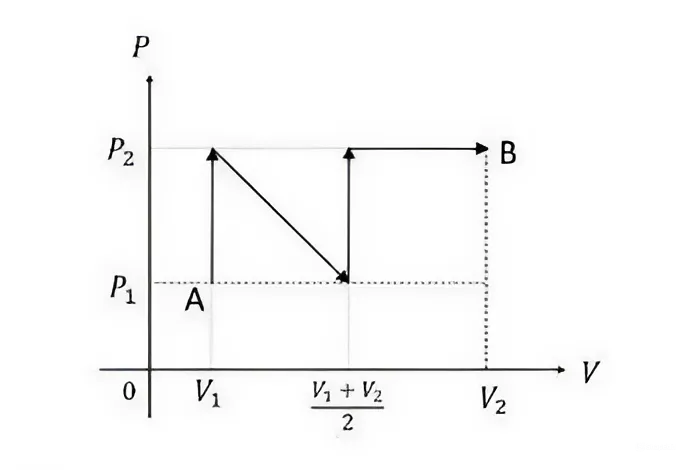
The work done \(W\) in this process is:
1) \(\frac{1}{4} (V_2 - V_1)(3P_2 + P_1)\)
2) \(\frac{1}{4} (V_2 - V_1)(3P_2 - P_1)\)
3) \(\frac{1}{2} (V_2 - V_1)(P_1 + P_2)\)
4) \(\frac{1}{2} (V_2 + V_1)(P_2 - P_1)\)
Check Answer
Option 1
Q.No:33 CSIR June-2025
A refrigerator can be thought to be a reversible engine operating between
\(T_{2} = 20^\circ\text{C}\) and \(T_{1} = -10^\circ\text{C}\).
The work needed to run this is supplied by another engine that takes in energy
at the rate of 500 W and runs with 50% efficiency.
If the refrigerator freezes 5 kg of water at \(0^\circ\text{C}\)
(latent heat \(Q_L = 334\ \text{kJ/kg}\) for ice) in \(n\) hours,
then \(n\) is closest to:
1) 0.4
2) 0.3
3) 0.1
4) 0.2
Check Answer
Option 4
Q.No:34 CSIR June-2025
The internal energy of a system is given by
\( U = g(N)\, V^{-2/3} \exp\left[\frac{2S}{3NR}\right] \),
where \(V\) is the volume, \(S\) is the entropy, \(N\) is the number of molecules,
and \(R\) is a constant. The function \(g(N)\) is proportional to:
1) \(N^{5/3}\)
2) \(N^{1/3}\)
3) \(N^{2/3}\)
4) \(N\)
Check Answer
Option 1
Q.No:35 CSIR June-2025
A thermodynamic system (at temperature \(T\) and volume \(V\)) is described by its internal
energy \(U = A T^{4} V\) and pressure \(p = \frac{1}{3} A T^{4}\), where \(A\) is a constant
of appropriate dimension. The Helmholtz free energy of the system is:
1) \(\frac{4}{3} A T^{4} V\)
2) \(\frac{1}{3} A T^{4} V\)
3) \(-\frac{1}{3} A T^{4} V\)
4) \(-\frac{4}{3} A T^{4} V\)
