Q.No:1 JEST-2012
Consider an ideal gas of mass \(m\) at temperature \(T_1\) which is mixed isobarically (i.e. at constant pressure) with an equal mass of same gas at temperature \(T_2\) in a thermally insulated container. What is the change of entropy of the universe?
(a)
\(2mC_p\ln{\left(\frac{T_1+T_2}{2\sqrt{T_1 T_2}}\right)}\)
(b)
\(2mC_p\ln{\left(\frac{T_1-T_2}{2\sqrt{T_1 T_2}}\right)}\)
(c)
\(2mC_p\ln{\left(\frac{T_1+T_2}{2T_1 T_2}\right)}\)
(d)
\(2mC_p\ln{\left(\frac{T_1-T_2}{2\sqrt{T_1 T_2}}\right)}\)
Check Answer
Option a
Q.No:2 JEST-2012
Efficiency of a perfectly reversible (Carnot) heat engine operating between absolute temperatures \(T\) and zero is equal to
(a)
\(0\)
(b)
\(0.5\)
(c)
\(0.75\)
(d)
\(1\)
Check Answer
Option d
Q.No:3 JEST-2012
A thermally insulated ideal gas of volume \(V_1\) and temperature \(T\) expands into another enclosure of volume \(V_2\) through a porous plug. What is the change in the temperature of the gas?
(a)
\(0\)
(b)
\(T\ln{(V_1/V_2)}\)
(c)
\(T\ln{(V_2/V_1)}\)
(d)
\(T\ln{[(V_2-V_1)/V_2]}\)
Check Answer
Option a
Q.No:4 JEST-2012
A monoatomic ideal gas at \(17^{\circ}\) is adiabatically compressed to \(1/8\) of its original volume. The temperature after compression is
(a)
\(2.1^{\circ}C\)
(b)
\(17^{\circ}C\)
(c)
\(-200.5^{\circ}C\)
(d)
\(887^{\circ}C\)
Check Answer
Option d
Q.No:5 JEST-2013
For a diatomic ideal gas near room temperature, what fraction of the heat supplied is available for external work if the gas is expanded at constant pressure?
(a)
\(1/7\)
(b)
\(5/7\)
(c)
\(3/4\)
(d)
\(2/7\)
Check Answer
Option d
Q.No:6 JEST-2013
A metal bullet comes to rest after hitting its target with a velocity of \(80 m/s\). If \(50\%\) of the heat generated remains in the bullet, what is the increase in its temperature? (The specific heat of the bullet \(=160\) Joule per Kg per degree C)
(a)
\(14^{\circ} C\)
(b)
\(12.5^{\circ} C\)
(c)
\(10^{\circ} C\)
(d)
\(8.2^{\circ} C\)
Check Answer
Option c
Q.No:7 JEST-2014
Ice of density \(\rho_1\) melts at pressure \(P\) and absolute temperature \(T\) to form water of density \(\rho_2\). The latent heat of melting of \(1\) gram of ice is \(L\). What is the change in the internal energy \(\Delta U\) resulting from the melting of \(1\) gram of ice?
(a)
\(L+P\left(\frac{1}{\rho_2}-\frac{1}{\rho_1}\right)\)
(b)
\(L-P\left(\frac{1}{\rho_2}-\frac{1}{\rho_1}\right)\)
(c)
\(L-P\left(\frac{1}{\rho_1}-\frac{1}{\rho_2}\right)\)
(d)
\(L+P\left(\frac{1}{\rho_1}-\frac{1}{\rho_2}\right)\)
Check Answer
Option Grace
Q.No:8 JEST-2014
A \(100\) ohms resistor carrying current of \(1\) Amp is maintained at a constant temperature of \(30^{\circ}C\) by a heat bath. What is the rate of entropy increase of the resistor?
(a)
\(3.3 Joules/K/sec\)
(b)
\(6.6 Joules/K/sec\)
(c)
\(0.33 Joules/K/sec\)
(d)
None of the above
Check Answer
Option d
Q.No:9 JEST-2014
For which gas the ratio of specific heats (\(C_p/C_v\)) will be the largest?
(a)
mono-atomic
(b)
di-atomic
(c)
tri-atomic
(d)
hexa-atomic
Check Answer
Option a
Q.No:10 JEST-2015
An ideal gas is compressed adiabatically from an initial volume \(V\) to a final volume \(\alpha V\) and a work \(W\) is done on the system in doing so. The final pressure of the gas will be \(\left(\gamma=\frac{C_P}{C_V}\right)\)
(a)
\(\frac{W}{V^{\gamma}}\frac{1-\gamma}{\alpha-\alpha^{\gamma}}\)
(b)
\(\frac{W}{V^{\gamma}}\frac{\gamma-1}{\alpha-\alpha^{\gamma}}\)
(c)
\(\frac{W}{V}\frac{1-\gamma}{\alpha-\alpha^{\gamma}}\)
(d)
\(\frac{W}{V}\frac{\gamma-1}{\alpha-\alpha^{\gamma}}\)
Check Answer
Option c
Q.No:11 JEST-2015
The entropy-temperature diagram of two Carnot engines, \(A\) and \(B\), are shown in the figure 4. The efficiencies of the engines are \(\eta_A\) and \(\eta_B\) respectively. Which one of the following equalities is correct?

(a)
\(\eta_A=\frac{\eta_B}{2}\)
(b)
\(\eta_A=\eta_B\)
(c)
\(\eta_A=3\eta_B\)
(d)
\(\eta_A=2\eta_B\)
Check Answer
Option d
Q.No:12 JEST-2016
An ideal gas with adiabatic exponent \(\gamma\) undergoes a process in which its pressure \(P\) is related to its volume \(V\) by the relation \(P=P_0-\alpha V\), where \(P_0\) and \(\alpha\) are positive constants. The volume starts from being very close to zero and increases monotonically to \(P_0/\alpha\). At what value of the volume during the process does the gas have maximum entropy?
(A)
\(\frac{P_0}{\alpha(1+\gamma)}\)
(B)
\(\frac{\gamma P_0}{\alpha(1-\gamma)}\)
(C)
\(\frac{\gamma P_0}{\alpha(1+\gamma)}\)
(D)
\(\frac{P_0}{\alpha(1-\gamma)}\)
Check Answer
Option C
Q.No:13 JEST-2016
An ideal gas has a specific heat ratio \(C_P/C_V=2\). Starting at a temperature \(T_1\) the gas undergoes an isothermal compression to increase its density by a factor of two. After this an adiabatic compression increases its pressure by a factor of two. The temperature of the gas at the end of the second process would be:
(A)
\(T_1/2\)
(B)
\(\sqrt{2}T_1\)
(C)
\(2T_1\)
(D)
\(T_1/\sqrt{2}\)
Check Answer
Option B
Q.No:14 JEST-2017
After the detonation of an atom bomb, the spherical ball of gas was found to be of \(15\) meter radius at a temperature of \(3\times 10^5 K\). Given the adiabatic expansion coefficient \(\gamma=5/3\), what will be the radius of the ball when its temperature reduces to \(3\times 10^3 K\)?
(A)
\(156 m\)
(B)
\(50 m\)
(C)
\(150 m\)
(D)
\(100 m\)
Check Answer
Option C
Q.No:15 JEST-2017
Suppose that the number of microstates available to a system of \(N\) particles depends on \(N\) and the combined variable \(UV^2\), where \(U\) is the internal energy and \(V\) is the volume of the system. The system initially has volume \(2 m^3\) and energy \(200 J\). It undergoes an isentropic expansion to volume \(4 m^3\). What is the final pressure of the system in SI units?
Check Answer
Ans 25
Q.No:16 JEST-2018
In a thermodynamic process, the volume of one mole of an ideal is varied as \(V=aT^{-1}\), where \(a\) is a constant. The adiabatic exponent of the gas is \(\gamma\). What is the amount of heat received by the gas if the temperature of the gas increases by \(\Delta T\) in the process?
(A)
\(R\Delta T\)
(B)
\(\frac{R\Delta T}{1-\gamma}\)
(C)
\(\frac{R\Delta T}{2-\gamma}\)
(D)
\(R\Delta T\frac{2-\gamma}{\gamma-1}\)
Check Answer
Option D
Q.No:17 JEST-2018
A theoretical model for a real (non-ideal) gas gives the following expressions for the internal energy (\(U\)) and the pressure (\(P\)),
\[
U(T, V)=aV^{-2/3}+bV^{2/3} T^2,
\]
and
\[
P(T, V)=\frac{2}{3}aV^{-5/3}+\frac{2}{3}bV^{-1/3} T^2,
\]
where \(a\) and \(b\) are constants. Let \(V_0\) and \(T_0\) be the initial volume and initial temperature respectively. If the gas expands adiabatically, the volume of the gas is proportional to
(A)
\(T\)
(B)
\(T^{3/2}\)
(C)
\(T^{-3/2}\)
(D)
\(T^{-2}\)
Check Answer
Option C
Q.No:18 JEST-2018
A frictionless, heat conducting piston of negligible mass and heat capacity divides a vertical, insulated cylinder of height \(2H\) and cross sectional area \(A\) into two halves. Each half contains one mole of an ideal gas at temperature \(T_0\) and pressure \(P_0\) corresponding to STP. The heat capacity ratio \(\gamma=C_p/C_v\) is given. A load of weight \(W\) is tied to the piston and suddenly released. After the system comes to equilibrium, the piston is at rest and the temperatures of the gases in the two compartments are equal. What is the final displacement \(y\) of the piston from its initial position, assuming \(yW\gg T_0 C_v\)?
(A)
\(\frac{2H}{\sqrt{\gamma}}\)
(B)
\(H\gamma\)
(C)
\(\frac{H}{\sqrt{\gamma}}\)
(D)
\(\frac{2H}{\gamma}\)
Check Answer
Option C
Q.No:19 JEST-2018
An ideal fluid is subjected to a thermodynamic process described by \(\rho=CV^{-\alpha}\) and \(P=n\rho^{\Gamma}\), where \(\rho\) is energy density and \(P\) is pressure. For what values of \(n\) and \(\Gamma\), the process is adiabatic if the volume is changed slowly?
(A)
\(\Gamma=\alpha-1, n=1\)
(B)
\(\Gamma=1-\alpha, n=\alpha\)
(C)
\(\Gamma=1, n=\alpha-1\)
(D)
\(\Gamma=\alpha, n=1-\alpha\)
Check Answer
Option C
Q.No:20 JEST-2018
In an experiment, certain quantity of an ideal gas at temperature \(T_0\), pressure \(P_0\) and volume \(V_0\) is heated by a current flowing through a wire for a duration of \(t\) seconds. The volume is kept constant and the pressure changes to \(P_1\). If the experiment is performed at constant pressure strting with the same initial conditions, the volume changes from \(V_0\) to \(V_1\). The ratio of the specific heats at constant pressure and constant volume is
(A)
\(\frac{P_1-P_0}{V_1-V_0}\frac{V_0}{P_0}\)
(B)
\(\frac{P_1-P_0}{V_1-V_0}\frac{V_1}{P_1}\)
(C)
\(\frac{P_1 V_1}{P_0 V_0}\)
(D)
\(\frac{P_0 V_0}{P_1 V_1}\)
Check Answer
Option A
Q.No:21 JEST-2019
Two joggers \(A\) and \(B\) are running at a steady pace around a circular track. \(A\) takes \(T_A\) minutes whereas \(B\) takes \(T_B\) (\(>T_A\)) minutes to complete one round. Assuming that they have started together, what will be time taken by \(A\) to overtake \(B\) for the first time?
(A)
\(\frac{2\pi}{T_A-T_B}\)
(B)
\(\frac{1}{T_A}-\frac{1}{T_B}\)
(C)
\(\frac{1}{T_A+T_B}\)
(D)
\(\left(\frac{1}{T_A}-\frac{1}{T_B}\right)^{-1}\)
Check Answer
Option D
Q.No:22 JEST-2019
A diatomic ideal gas at room temperature, is expanded at a constant pressure \(P_0\). If the heat absorbed by the gas is \(Q=14\) Joules, what is the maximum work in Joules that can be extracted from the system?
Check Answer
Ans 4
Q.No:23 JEST-2020
Consider a classical harmonic oscillator in thermal equilibrium at a temperature \(T\). If the spring constant is changed to twice its value isothermally, then the amount of work done on the system is
(A)
\(k_B T\ln{2}\)
(B)
\(k_B T\frac{\ln{2}}{2}\)
(C)
\(2k_B T\ln{2}\)
(D)
\(-k_B T\ln{2}\)
Check Answer
Option B
Q.No:24 JEST-2020
A rod consists of two equal sections of length \(\ell\) each with coefficient of thermal conductivity \(\kappa_1\) and \(\kappa_2\), respectively. One end of the rod is kept at a fixed temperature \(T_1\) and the other end at a temperature \(T_2\) (\(T_1>T_2\)). If \(\kappa_2=2\kappa_1\) then the temperature at the interface is

(A)
\(T=(2T_1-T_2)/3\)
(B)
\(T=(2T_1+T_2)/3\)
(C)
\(T=(T_1+2T_2)/3\)
(D)
\(T=(T_1-2T_2)/3\)
Check Answer
Option C
Q.No:25 JEST-2020
Two compartments in a cylinder with uniform cross section and total length \(102 cm\) are separated by a sliding partition which can move but does not allow heat to pass across it. No molecules are present in either of the compartments. The radiation inside each compartment is in thermal equilibrium with its walls. The walls at the two ends of the cylinder are maintained at temperatures \(2000 K\) and \(4000 K\), respectively. The sides are perfectly insulated. Find the location of the partition, measured from the left end of the container.

Check Answer
Ans 6
Q.No:26 JEST-2021
The free energy density of a gas at a constant temperature is given by \(f(\rho)=C\rho\ln{(\rho/\rho_0)}\), where \(\rho\) represents the density of the gas, while \(C\) and \(\rho_0\) are positive constants. The pressure of the system is
(A)
\(C\rho\)
(B)
\(C\rho^2/\rho_0\)
(C)
\(C\rho_0\ln{(\rho/\rho_0)}\)
(D)
\(C\rho\ln{(\rho/\rho_0)}\)
Check Answer
Option A
Q.No:27 JEST-2021
\(M\) grams of water at temperature \(T_a\) is adiabatically mixed with an equal mass of water at temperature \(T_b\). keeping the pressure constant. Find the change in entropy of the system (specific heat of water is \(C_p\)) .
(A)
\(\Delta S=MC_p \ln{\left[1-\frac{(T_a-T_b)^2}{4T_a T_b}\right]}\)
(B)
\(\Delta S=MC_p \ln{\left[1+\frac{(T_a+T_b)^2}{4T_a T_b}\right]}\)
(C)
\(\Delta S=MC_p \ln{\left[1+\frac{(T_a-T_b)^2}{4T_a T_b}\right]}\)
(D)
\(\Delta S=MC_p \ln{\left[\frac{T_a+T_b}{(4T_a T_b)^{1/2}}\right]}\)
Check Answer
Option C
Q.No:28 JEST-2021
A large box of volume \(V\) is fitted with a vertical glass tube of cross-sectional area \(A\), in which a metal ball of mass \(m\) fits exactly. The box contains an ideal gas at a pressure slightly higher than atmospheric pressure \(P\) because of the weight of the ball. If the ball is displaced slightly from equilibrium, find the angular frequency \(\omega\) of simple harmonic oscillations. Assume adiabatic behaviour, with ratio of specific heats \(\gamma=C_p/C_V\).
(A)
\(\omega=\sqrt{\frac{A^2(P+mg/A)}{2\gamma Vm}}\)
(B)
\(\omega=\sqrt{\frac{2\gamma A^2(P+mg/A)}{Vm}}\)
(C)
\(\omega=\sqrt{\frac{A^2(P+mg/A)}{\gamma Vm}}\)
(D)
\(\omega=\sqrt{\frac{\gamma A^2(P+mg/A)}{Vm}}\)
Check Answer
Option D
Q.No:29 JEST-2022
An ideal diatomic gas at pressure \(P\) is adiabatically compressed so that its volume becomes \(\frac{1}{n}\) times the initial value. The final pressure of the gas will be
(a)
\(n^{\frac{7}{5}}P\)
(b)
\(n^{\frac{7}{2}}P\)
(c)
\(n^{-\frac{7}{5}}P\)
(d)
\(n^{\frac{5}{3}}P\)
Check Answer
Option a
Q.No:30 JEST-2022
One mole of an ideal gas undergoes a thermodynamic cycle formed by an isobaric process, an isochoric process, and an adiabatic process (see figure). At A, the temperature of the gas is \(T\). What is the change in the internal energy of the gas, in the units of \(RT\) (\(R\) is the universal gas constant) as the system goes from A to B
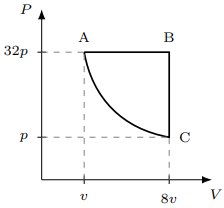
Check Answer
Ans 17.50
Q.No:31 JEST-2023
Using the first law of thermodynamics \(dU = T dS -P dV\) , and the definitions of the thermodynamic potentials \(H = U + P V , F = U - T S\), \(G = H - T S\), work out the four Maxwell relations. Using these compute :
\[
\chi = \left(\frac{\partial T}{\partial V}\right)_S + \left(\frac{\partial T}{\partial P}\right)_S + \left(\frac{\partial P}{\partial T}\right)_V + \left(\frac{\partial V}{\partial T}\right)_P
\]
Which of the following does \(\chi\) equal?
(a) \(
\left(\frac{\partial S}{\partial V}\right)_T - \left(\frac{\partial S}{\partial P}\right)_T + \left(\frac{\partial V}{\partial S}\right)_P - \left(\frac{\partial P}{\partial S}\right)_V
\)
(b) \(
\left(\frac{\partial S}{\partial V}\right)_T - \left(\frac{\partial S}{\partial P}\right)_T + \left(\frac{\partial V}{\partial S}\right)_P + \left(\frac{\partial P}{\partial S}\right)_V
\)
(c) \(
\left(\frac{\partial S}{\partial V}\right)_T + \left(\frac{\partial S}{\partial P}\right)_T + \left(\frac{\partial V}{\partial S}\right)_P - \left(\frac{\partial P}{\partial S}\right)_V
\)
(d) \(
\left(\frac{\partial S}{\partial V}\right)_T + \left(\frac{\partial S}{\partial P}\right)_T + \left(\frac{\partial V}{\partial S}\right)_P + \left(\frac{\partial P}{\partial S}\right)_V
\)
Check Answer
option a
Q.No:32 JEST-2023
One mole of an isolated ideal gas in equilibrium at pressure \(P_1\), volume \(V_1\), and temperature \(T_1\) undergoes a process that changes its state. In the final state the gas is in equilibrium at pressure
\(P_2\), volume \(V_2\), and temperature \(T_2\). Suppose the ratios of the final and initial temperatures and pressures are
\[\eta_T=\frac{T_2}{T_1}, \hspace{5mm} \eta_P=\frac{P_2}{P_1}.\]
Work out the change in entropy \(\Delta S\) in the process. Take the heat capacities of the gas at constant pressure and constant volume to be \(C_p\) and \(C_v\) respectively, and the ideal gas constant to be \(R\).
(a) \(C_p \hspace{0.5mm} ln \hspace{0.5mm} (\eta_T) -R \hspace{0.5mm} ln \hspace{0.5mm} (\eta_P) \)
(b) \(C_p \hspace{0.5mm} ln \hspace{0.5mm} (\eta_T) +R \hspace{0.5mm} ln \hspace{0.5mm} (\eta_P) \)
(c)\(C_v \hspace{0.5mm} ln \hspace{0.5mm} (\eta_T) -R \hspace{0.5mm} ln \hspace{0.5mm} (\eta_P) \)
(d) \(C_v \hspace{0.5mm} ln \hspace{0.5mm} (\eta_T) +R \hspace{0.5mm} ln \hspace{0.5mm} (\eta_P) \)
Check Answer
option a
Q.No:33 JEST-2023
A steam engine takes steam from a boiler at \(200^\circ C\) (pressure \(1.5 \times 10^6\) Pa) and exhausts directly into the air at \(100^\circ C\) (pressure \(10^5\) Pa) . The maximum possible efficiency is closest to:
(a) \(78\%\)
(b) \(21\%\)
c) \(50\%\)
(d) \(93\%\)
Check Answer
option b
Q.No:34 JEST-2024
The ratio of the molar specific heats of an ideal gas is \( \gamma = \frac{C_p}{C_v} = \frac{3}{2} \). It undergoes a reversible isothermal expansion in which its volume doubles. Next, it undergoes a reversible isochoric process such that the change in entropy of the second process is equal to the change in entropy of the first process. What is the ratio of the final temperature to the initial temperature?
(a) \( \sqrt{2} \)
(b) \( 2 \)
(c) \( 3 \)
(d) \( \frac{3}{2} \)
Check Answer
option a
Q.No:35 JEST-2024
Given that the latent heat of liquefaction is 80 Cal/g, what is the change in entropy when 10 g of ice at 0°C is converted into water at the same temperature?
(a) \( 2.93 \) Cal K\(^{-1}\)
(b) \( 3.42 \) Cal K\(^{-1}\)
(c) \( 2.0 \) Cal K\(^{-1}\)
(d) \( 4.5 \) Cal K\(^{-1}\)
Check Answer
option a
Q.No:36 JEST-2024
Which of the following functions is not a valid thermodynamic function of internal energy \( U \) in terms of entropy \( S \), volume \( V \), and number of particles \( N \)? Here \( U_0 \), \( \alpha \), \( \beta \), \( A \), \( B \) and \( C \) are constants.
(a) \( U_0 \exp \left( \frac{aV^2 N}{S^2} \right) \)
(b) \( \left( \frac{AV^2}{N} \right) \exp \left( \frac{B VN}{S^2} \right) \)
(c) \( \frac{BS^2 V^2}{N^3} \)
(d) \( \frac{CN^2}{\sqrt{SV}} \)
Check Answer
option a
Q.No:37 JEST-2024
An ideal gas initially at pressure \( P_i \) undergoes the following sequence of processes:
1) A reversible adiabatic expansion that doubles its volume.
2) A reversible isothermal compression that restores its original volume.
3) A reversible isothermal expansion that doubles its volume.
4) A reversible adiabatic compression that restores its original volume.
If the final pressure of the gas is \( P_f \), which of the following is true?
(a) \( P_f = P_i \).
(b) \( P_f > P_i \).
(c) \( P_f < P_i \).
(d) The relation between \( P_f \) and \( P_i \) depends on the initial conditions.
Check Answer
option a
Q.No:38 JEST-2025
One mole of an ideal gas with a constant \(C_V\) undergoes a reversible adiabatic expansion.
Which one of the following equations is valid?
\(\gamma = \frac{C_P}{C_V}\) for the gas.
a) \(P^{\gamma - 1} T^{\gamma} = \text{constant}\)
b) \(V T^{\gamma} = \text{constant}\)
c) \(V^{\gamma} T = \text{constant}\)
d) \(P^{1 - \gamma} T^{\gamma} = \text{constant}\)
Check Answer
option d
Q.No:39 JEST-2025
Which of the following thermodynamic variables is not a function of state for an ideal gas?
a) None of the others
b) Pressure
c) Entropy
d) Temperature
Check Answer
option a
Q.No:40 JEST-2025
Given an isolated thermodynamic system with total energy \(E\), total volume \(V\)
and total number of particles \(N\), the condition for stable thermal equilibrium,
in terms of its entropy \(S\) under small changes \(\Delta E\) and \(\Delta V\), is given by
a) \(−S(E + ΔE, V + ΔV, N) + S(E − ΔE, V − ΔV, N) − 2S(E, V, N) < 0\)
b) \(S(E + ΔE, V + ΔV, N) + S(E − ΔE, V − ΔV, N) + 2S(E, V, N) < 0\)
c) \(S(E + ΔE, V + ΔV, N) − S(E − ΔE, V − ΔV, N) − 2S(E, V, N) < 0\)
d) \(S(E + ΔE, V + ΔV, N) + S(E − ΔE, V − ΔV, N) − 2S(E, V, N) < 0\)
Check Answer
option d
Q.No:41 JEST-2025
A heat engine works between a high temperature source and a sink at \(27^\circ\mathrm{C}\).
If the maximum possible efficiency for it to achieve is 50%, what is the temperature of the source in \(^{\circ}\mathrm{C}\)?
Check Answer
Ans 327
Q.No:42 JEST-2025
A current of \(10\ \mathrm{A}\) is maintained for \(1\ \mathrm{s}\) in a resistor of resistance \(25\ \Omega\), which is thermally insulated.
The initial temperature of the resistor is \(23^\circ\mathrm{C}\).
The resistor has a mass of \(10\ \mathrm{g}\) and a specific heat of \(836\ \mathrm{J\,kg^{-1}\,K^{-1}}\).
What is the entropy change of the resistor, rounding off to the nearest whole number, in units of \(\mathrm{J\,K^{-1}}\)?
