Vector Calculus GATE , CSIR , JEST & TIFR - S. N. Bose Physics Learning Center

Q.No:1 GATE-2012

Given \(\vec{F}=\vec{r}\times \vec{B}\), where \(\vec{B}=B_0(\hat{i}+\hat{j}+\hat{k})\) is a constant vector and \(\vec{r}\) is the position vector. The value of \(\oint_C \vec{F}\cdot d\vec{r}\), where \(C\) is a circle of unit radius centered at origin is,

(A) \(0\)

(B) \(2\pi B_0\)

(D) \(1\)

Check Answer

Option C

Q.No:2 GATE-2013

For a scalar function \(\varphi\) satisfying the Laplace equation, \(\nabla \varphi\) has

(A) zero curl and non-zero divergence

(B) non-zero curl and zero divergence

(D) non-zero curl and non-zero divergence

Check Answer

Option C

Q.No:3 GATE-2013

If \(\vec{A}\) and \(\vec{B}\) are constant vectors, then \(\nabla(\vec{A}\cdot \vec{B}\times \vec{r})\) is

(A) \(\vec{A}\cdot \vec{B}\)

(B) \(\vec{A}\times \vec{B}\)

(D) Zero

Check Answer

Option B

Q.No:4 GATE-2014

The unit vector perpendicular to the surface \(x^2+y^2+z^2=3\) at the point \((1, 1, 1)\) is

(A) \(\frac{\hat{x}+\hat{y}-\hat{z}}{\sqrt{3}}\)

(B) \(\frac{\hat{x}-\hat{y}-\hat{z}}{\sqrt{3}}\)

(D) \(\frac{\hat{x}+\hat{y}+\hat{z}}{\sqrt{3}}\)

Check Answer

Option D

Q.No:5 GATE-2015

Four forces are given below in Cartesian and spherical polar coordinates.

(i) \(\vec{F}_1=K\exp{(-r^2/R^2)}\hat{r}\)

(ii) \(\vec{F}_2=K(x^3 \hat{y}-y^3 \hat{z})\)

(iii) \(\vec{F}_3=K(x^3 \hat{x}+y^3 \hat{y})\)

(iv) \(\vec{F}_4=K(\hat{\phi}/r)\)

where \(K\) is a constant. Identity the correct option.

(A) (iii) and (iv) are conservative but (i) and (ii) are not

(B) (i) and (ii) are conservative but (iii) and (iv) are not

(D) (i) and (iii) are conservative but (ii) and (iv) are not

Check Answer

Option D

Q.No:6 GATE-2016

The direction of \(\vec{\nabla}f\) for a scalar field \(f(x, y, z)=\frac{1}{2}x^2-xy+\frac{1}{2}z^2\) at the point \(P(1, 1, 2)\) is

(A) \(\frac{(-\hat{j}-2\hat{k})}{\sqrt{5}}\)

(B) \(\frac{(-\hat{j}+2\hat{k})}{\sqrt{5}}\)

(D) \(\frac{(\hat{j}+2\hat{k})}{\sqrt{5}}\)

Check Answer

Option B

Q.No:7 GATE-2018

In spherical polar coordinates \((r, \theta, \phi)\), the unit vector \(\hat{\theta}\) at \((10, \pi/4, \pi/2)\) is

(A) \(\hat{k}\)

(B) \(\frac{1}{\sqrt{2}}(\hat{j}+\hat{k})\)

(D) \(\frac{1}{\sqrt{2}}(\hat{j}-\hat{k})\)

Check Answer

Option D

Q.No:8 GATE-2023

Consider the vector field \(\vec{V}\) consisting of the velocities of points on a thin horizontal disc of radius \(R=2m\), moving anticlockwise with uniform angular speed \(\omega=2\) rad/sec about an axis passing through its center. If \(V=|\vec{V}|\), then which of the following options is(are) CORRECT ? (In the options, \(\hat{r}\) and \(\hat{\theta}\) are unit vectors corresponding to the plane polar coordinates \(r\) and \(\theta\)).

You may use the fact that in cylindrical coordinates (\(z, \phi , z\)) (s is the distance from the z-axis), the gradient, divergence, curl and Laplacian operators are:

\(\vec{\nabla}=\frac{\partial f}{\partial s}\hat{s} +\frac{1}{s}\frac{\partial f}{\partial \phi } \hat{\phi}+ \frac{\partial f}{\partial z }\hat{z}\);

\(\vec{\nabla} \cdot \vec{A}=\frac{1}{s} \frac{\partial}{\partial s}(s \hspace{0.5mm} A_s)+\frac{1}{s} \frac{\partial A_{\phi}}{\partial \phi} +\frac{\partial A_z}{\partial z}\);

\(\vec{\nabla}\times \vec{A}=(\frac{1}{s}\frac{\partial A_{z}}{\partial \phi}-\frac{\partial A_{\phi}}{\partial z})\hat{s}+(\frac{\partial A_{s}}{\partial z}-\frac{\partial A_{z}}{\partial s})\hat{\phi}+\frac{1}{s}(\frac{\partial }{\partial s} (s A_\phi ) -\frac{\partial A_{s}}{\partial \phi}) \hat{z}\); \(\vec{\nabla}^2 f=\frac{1}{s}\frac{\partial }{\partial s}(s \frac{\partial f}{\partial s})+\frac{1}{s^2}\frac{ \partial^2 f}{\partial \phi^2}+\frac{ \partial^2 f}{\partial z^2}\)

(A) \(\vec{\nabla} V =2\hat{r}\)

(B) \(\vec{\nabla} \cdot V =2\)

(C) \(\vec{\nabla} \times \vec{V}=4\hat{z}\), where \(\hat{z}\) is a unit vector perpendicular to the (\(r, \theta\)) plane

(D) \(\vec{\nabla}^2 V =\frac{4}{3}\) at \(r=1.5\) m

Check Answer

Option A, C, D

Q.No:9 GATE-2024

Consider a vector field \(\vec{F} = (2xz + 3y^2)\hat{y} + 4yz^2\hat{z}\). The closed path (\(\Gamma\): A \(\rightarrow\) B \(\rightarrow\) C \(\rightarrow\) D \(\rightarrow\) A) in z = 0 plane is shown in figure.

\[ \oint_{\Gamma} \vec{F} \cdot d\vec{l} \text{ denotes the line integral of } \vec{F} \text{ along the closed path } \Gamma.\] Which of the following option is/are true?\\ {MSQ}

(A) \(\oint_{\Gamma} \vec{F} \cdot d\vec{l} = 0\)

(B) \(\vec{F}\) is non-conservative

(D) \(\vec{F}\) can be written as the gradient of a scalar field

Check Answer

Option A, B

Q.No:10 GATE-2024

Consider a volume integral \[ I = \int_V \nabla^2 \left(\frac{1}{r}\right) dV \] over a volume \( V \), where \( r = \sqrt{x^2 + y^2 + z^2} \). Which of the following statement is/are correct?

(A) \( I = -4\pi \), if \( r = 0 \) is inside the volume \( V \)

(B) Integrand vanishes for \( r \neq 0 \)

(D) Integrand diverges as \( r \rightarrow \infty \)

Check Answer

Option A, B,C

Q.No:1 CSIR Dec-2014

(1) \(\vec{\mathbf{\nabla}}\cdot \vec{\mathbf{r}}=0\) and \(\vec{\mathbf{\nabla}}\times \vec{\mathbf{r}}=\vec{\mathbf{r}}/r\)

(2) \(\vec{\mathbf{\nabla}}\cdot \vec{\mathbf{r}}=0\) and \(\nabla^2 r=0\)

(3) \(\vec{\mathbf{\nabla}}\cdot \vec{\mathbf{r}}=3\) and \(\nabla^2 \vec{\mathbf{\nabla}}=\vec{\mathbf{\nabla}}/r^2\)

(4) \(\vec{\mathbf{\nabla}}\cdot \vec{\mathbf{r}}=3\) and \(\vec{\mathbf{\nabla}}\times \vec{\mathbf{r}}=0\)

Check Answer

Option 4

Q.No:2 CSIR Dec-2019

The values of \(a\) and \(b\) for which the force \(\mathbf{F}=(axy+z^3)\hat{i}+x^2\hat{j}+bxz^2 \hat{k}\) is conservative are

(1) \(a=2, b=3\)

(2) \(a=1, b=3\)

(3) \(a=2, b=6\)

(4) \(a=3, b=2\)

Check Answer

Option 1

Q.No:3 CSIR Feb-2022

The volume integral \(\iint_V\int \vec{A}.(\vec{\nabla}\times \vec{A})d^3x \), is over a region \(V\) bounded by a surface \(sum\) (an infinitesimal area element being \(\hat{n}ds\) , where \(\hat{n}\) is the outward unit normal). If it changes to \(I+\Delta I\) when the vector \(\vec{A}\) is changed to \(A+\Delta \Lambda\) , then \(\Delta I\) can be expressed as

(1) \(\iint_V\int \vec{\Delta}.(\vec{\Delta}\Lambda\times\vec{A})d^3x\)

(2) \(\iint_V\int\Delta^2\Lambda d^3x\)

(3) \(-\oint_{\sum}(\vec{\Delta}\Lambda\times\vec{A}).\hat{n}ds\)

(4) \(\oint_{\sum}\Delta^2\Lambda.\hat{n}ds\)

Check Answer

Option 3

Q.No: 4 CSIR June-2024

Vorticity of a vector field \(\vec{B}\) is defined as \(\vec{V} = \vec{\nabla} \times \vec{B}\). Given \(\vec{B} = kxyz\hat{r}\), where \(k\) is a constant, which one of the following is correct?

1) Vorticity is a null vector for all finite \(x, y, z\).

2) Vorticity is parallel to the vector field everywhere.

3) The angle between vorticity and vector field depends on \(x, y, z\).

4) Vorticity is perpendicular to the vector field everywhere.

Check Answer

Option 4

Q.No:1 JEST-2013

The vector field \(xz\hat{i}+y\hat{j}\) in cylindrical polar coordinates is

(a) \(\rho(z\cos^2{\phi}+\sin^2{\phi})\hat{e}_{\rho}+\rho\sin{\phi}\cos{\phi}(1-z)\hat{e}_{\phi}\)

(b) \(\rho(z\cos^2{\phi}+\sin^2{\phi})\hat{e}_{\rho}+\rho\sin{\phi}\cos{\phi}(1+z)\hat{e}_{\phi}\)

(d) \(\rho(z\sin^2{\phi}+\cos^2{\phi})\hat{e}_{\rho}+\rho\sin{\phi}\cos{\phi}(1-z)\hat{e}_{\phi}\)

Check Answer

Option a

Q.No:2 JEST-2016

Given the condition \(\nabla^2 \Phi=0\), the solution of the equation \(\nabla^2 \Psi=k\vec{\nabla}\Phi\cdot \vec{\nabla}\Phi\) is given by:

(A) \(\Psi=k\Phi^2/2\)

(B) \(\Psi=k\Phi^2\)

(D) \(\Psi=k\Phi\ln{\Phi}/2\)

Check Answer

Option A

Q.No:3 JEST-2017

The temperature in a rectangular plate bounded by the lines \(x=0, y=0, x=3\) and \(y=5\) is \(T=xy^2-x^2 y+100\). What is the maximum temperature difference between two points on the plate?

Check Answer

Ans 38

Q.No:4 JEST-2017

What is the equation of the plane which is tangent to the surface \(xyz=4\) at the point \((1, 2, 2)\)?

(A) \(x+2y+4z=12\)

(B) \(4x+2y+z=12\)

(D) \(2x+y+z=6\)

Check Answer

Option D

Q.No:5 JEST-2019

Suppose \(\psi\vec{A}\) is a conservative vector, \(\vec{A}\) is a non-conservative vector and \(\psi\) is non-zero scalar everywhere. Which one of the following is true?

(A) \((\nabla\times \vec{A})\cdot \vec{A}=0\)

(B) \(\vec{A}\times \nabla \psi=\vec{0}\)

(D) \((\nabla\times \vec{A})\times \vec{A}=\vec{0}\)

Check Answer

Option A

Q.No:6 JEST-2019

Let \(\vec{r}\) be the position vector of a point on a closed contour \(C\). What is the value of the line integral \(\oint \vec{r}.d\vec{r}\)?

(A) \(0\)

(B) \(\frac{1}{2}\)

(D) \(\pi\)

Check Answer

Option A

Q.No:7 JEST-2019

What is the angle (in degrees) between the surfaces \(y^2+z^2=2\) and \(y^2-x^2=0\) at the point \((1, -1, 1)\)?

Check Answer

Ans 60

Q.No:8 JEST-2021

Let \(ABCDEF\) be a regular hexagon. The vector \(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}+\overrightarrow{AE}+\overrightarrow{AF}\) will be

(a) \(0\)

(b) \(\overrightarrow{AD}\)

(d) \(3\overrightarrow{AD}\)

Check Answer

Option d

Q.No:9 JEST-2023

Given the vector \(\vec{v}=y \hat{i}+3x \hat{j}\), what is the value of the line integral \[\oint \vec{v} \cdot d \vec{r}\] along the unit circle (centered at the origin) in an anti-clockwise direction?

(a) \(\frac{2 \pi}{3}\)

(b) \(\pi\)

(d) \(2\pi\)

Check Answer

Option d

Q.No:10 JEST-2023

Which of the following vanishes identically?

(a) \(\nabla \times \frac{((y+x) \hat{i}+(y-x) \hat{j})}{x^2+y^2}\)

(b) \(\nabla \times \frac{(y \hat{i}-x \hat{j})}{x^2+y^2}\)

(d) \(\nabla \cdot [\frac{(x \hat{i}+y \hat{j}+x \hat{k})}{(x^2+y^2+z^2)^{3/2}}]\)

Check Answer

Option c

Q.No:11 JEST-2024

A magnetic vector potential is given as \( \vec{A} = 6\hat{i} + yz^2\hat{j} + (3y + z)\hat{k} \). Find the corresponding outgoing magnetic flux through the five faces (excluding the shaded one) of a unit cube with one corner at the origin, as shown in the figure.

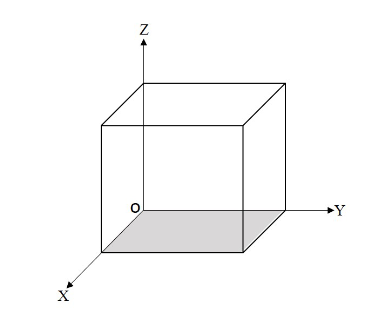
Check Answer

Ans 0

Q.No:12 JEST-2025

A particle is moving under the force field given by \(\vec{F}=k\vec{r}\), where \(k\) is a positive constant. The difference in work done (in arbitrary units) if the particle moves from point A \((-1,0,0)\) to point B \((1,0,0)\) following semi–circular paths in the clockwise and anti-clockwise directions on the X–Y plane will be

a) \(0\)

b) \(2\pi k\)

c) \(\pi k\)

d) \(\frac{1}{2}\pi k\)

Check Answer

Option a

Q.No:13 JEST-2025

Evaluate \(\vec{\nabla}\cdot (r^{4}\,\vec{r})\), where \(\vec{r}\) represents a three–dimensional position vector.

a) \(7r^{4}\)

b) \(4r^{4}\)

c) \(5r^{4}\)

d) \(0\)

Check Answer

Option a

Q.No:1 TIFR-2013

Consider the surface corresponding to the equation \[ 4x^2+y^2+z=0 \] A possible unit tangent to this surface at the point \((1, 2, -8)\) is

(a) \(\frac{1}{\sqrt{5}}\hat{i}-\frac{2}{\sqrt{5}}\hat{j}\)

(b) \(\frac{1}{5}\hat{j}-\frac{4}{5}\hat{k}\)

(d) \(-\frac{1}{\sqrt{5}}\hat{i}+\frac{3}{\sqrt{5}}\hat{j}-\frac{4}{\sqrt{5}}\hat{k}\)

Check Answer

Option a

Q.No:2 TIFR-2015

Which of the following vectors is parallel to the surface \(x^2 y+2xz=4\) at the point \((2, -2, 3)\)?

(a) \(+6\hat{i}-2\hat{j}-5\hat{k}\)

(b) \(+6\hat{i}+2\hat{j}+5\hat{k}\)

(d) \(+6\hat{i}-2\hat{j}+5\hat{k}\)

Check Answer

Option d

Q.No: 3 TIFR-2019

Consider the surface defined by \(ax^2+by^2+cz+d=0\), where \(a, b, c\) and \(d\) are constants. If \(\hat{n}_1\) and \(\hat{n}_2\) are unit normal vectors to the surface at the points \((x, y, z)=(1, 1, 0)\) and \((0, 0, 1)\) respectively, and \(\hat{m}\) is a unit vector normal to both \(\hat{n}_1\) and \(\hat{n}_2\), then \(\hat{m}=\)

(a) \(\frac{-a\hat{\mathbf{i}}+b\hat{\mathbf{j}}}{\sqrt{a^2+b^2}}\)

(b) \(\frac{b\hat{\mathbf{i}}-a\hat{\mathbf{j}}}{\sqrt{a^2+b^2}}\)

(d) \(\frac{a\hat{\mathbf{i}}-b\hat{\mathbf{j}}+c\hat{\mathbf{k}}}{\sqrt{a^2+b^2+c^2}}\)

Check Answer

Option b

Q.No: 4 TIFR-2022

Consider the two-dimensional polar integral \[P=\int dr \hspace{0.5mm} d\theta \hspace{0.5mm} r^{19} \hspace{0.5mm} e^{-r^2} \hspace{0.5mm} sin^8 \theta \hspace{0.5mm} cos^{11} \theta\] If the integration is over only the first quadrant \((0\leq \theta \leq \pi/2)\), the value of \(P\) is

(a) 180

(b) \(88 \pi\)

(d) \( 16 \pi\)

Check Answer

Option a

Q.No: 5 TIFR-2023

A surface is given by \[4x^2y-2xy^2+3z^3=0\] Which one of the following is a vector normal to it at the point \((2,3,1)\) ?

(a) \(30\hat{i}-8\hat{j}+9\hat{k}\)

(b) \(30\hat{i}-8\hat{j}-9\hat{k}\)

(d) \(30\hat{i}+8\hat{j}-9\hat{k}\)

Check Answer

Option a

Q.No: 6 TIFR-2024

A surface is given by \[ 2x^3z + 4y^2z + 3z^2 = 81 \] Which of the following is a vector tangential to it at the point on the surface with coordinates \((x, y, z) = (1,2,3)\)?

(a) \( 2\mathbf{\hat{i}} - 3\mathbf{\hat{j}} + 3\mathbf{\hat{k}} \)

(b) \( 18\mathbf{\hat{i}} + 48\mathbf{\hat{j}} + 36\mathbf{\hat{k}} \)

(d) \( -3\mathbf{\hat{i}} - 2\mathbf{\hat{j}} + 6\mathbf{\hat{k}} \)

Check Answer

Option a

Q.No: 7 TIFR-2025

Consider the triangle subtended on the surface of a sphere of radius \(1\) by joining the points \(\left(\frac{1}{2},\frac{\sqrt{3}}{2},0\right)\), \(\left(-\frac{1}{2},\frac{\sqrt{3}}{2},0\right)\), and \((0,0,1)\) with arcs of great circles. The area subtended by this triangle on the surface of the sphere is given by: (Hint: Drawing a figure might help.)

a) \(\frac{\pi}{3}\)

b) \(\frac{\sqrt{3}\,\pi}{2}\)

c) \(\sqrt{3}\,\pi\)

d) \(\frac{2\pi}{3}\)