Q.No:1 JAM-2015
Consider a vector field \(\vec{F}=y\hat{i}+xz^3\hat{j}-zy\hat{k}\). Let \(C\) be the circle \(x^2+y^2=4\) on the plane \(z=2\), oriented counter-clockwise. The value of the contour integral \(\oint_c\vec{F}\cdot d\vec{r}\) is
(A)
\(28 \pi\)
(B)
\(4 \pi\)
(C)
\(-4 \pi\)
(D)
\(-28 \pi\)
Check Answer
Option A
Q.No:2 JAM-2016
Consider a closed triangular contour traversed in counter-clockwise direction, as shown in the figure below.

The value of the integral, \(\oint \vec{F}\cdot \vec{dl}\) evaluated along this contour, for a vector field, \(\vec{F}=y\hat{e}_x-x\hat{e}_y\) is ____________ .
\((\hat{e}_x, \hat{e}_y\) and \(\hat{e}_y\) are unit vectors in Cartesian−coordinate system.)
Check Answer
Ans -2
Q.No:3 JAM-2016
A hemispherical shell is placed on the xy– plane centered at the origin. For a vector field
\(\vec{E}=(-y \hat{e}_x+x\hat{e}_y)/(x^2+y^2)\) the value of the integral \(\int_s (\vec{\nabla}\times \vec{E})\cdot \hspace{1mm}d\vec{a}\) over the hemispherical
surface is __________\(\pi\).
(\(d\vec{a}\) is the elemental surface area. \(\hat{e}_x,\hat{e}_y\) and \(\hat{e}_z\) are unit vectors in Cartesian −coordinate system.)
Check Answer
Ans 2 OR (-2)
Q.No:4 JAM-2016
The tangent line to the curve \(x^2+x y+5=0\) at (1,1) is represented by
(A)
\(y=3x-2\)
(B)
\(y=-3x+4\)
(C)
\(x=3y-2\)
(D)
\(x=-3y+4\)
Check Answer
Option MTA
Q.No:5 JAM-2017
The integral of the vector \(\vec{A}(\rho ,\varphi, z)=\frac{40}{\rho} cos \hspace{0.5mm}\varphi \hspace{0.5mm}\hat{\rho}\) (standard notation for cylindrical
coordinates is used) over the volume of a cylinder of height \(L\) and radius \(R_0\) is :
(A)
\(20\pi R_0L(\hat{i}+\hat{j})\)
(B)
0
(C)
\(40\pi R_0L\hat{j}\)
(D)
\(40\pi R_0L\hat{i}\)
Check Answer
Option D
Q.No:6 JAM-2017
The volume integral of the function \(f(r,\theta ,\phi)=r^2 \hspace{1mm} cos\theta\) over the region \((0\leq r\leq 2, 0\leq \theta \leq \pi/3\) and \(0\leq \phi \leq 2\pi)\) is ________________.
(Specify your answer to two digits after the decimal point)
Check Answer
Ans 15.0-15.15
Q.No:7 JAM-2018
Let \(f(x,y)=x^3-2y^3\). The curve along which \(\nabla^2 f=0\) is
(A)
\(x=\sqrt{2}y\)
(B)
\(x=2y\)
(C)
\(x=\sqrt{6}y\)
(D)
\(x=-y/2\)
Check Answer
Option B
Q.No:8 JAM-2018
A curve is given by \(\vec{r}(t)=t\hat{i}+t^2\hat{j}+t^3\hat{k}\).The unit vector of the tangent to the curve at \(t=1\) is
(A)
\(\frac{\hat{i}+\hat{j}+\hat{k}}{\sqrt{3}}\)
(B)
\(\frac{\hat{i}+\hat{j}+2\hat{k}}{\sqrt{6}}\)
(C)
\(\frac{\hat{i}+2\hat{j}+2\hat{k}}{3}\)
(D)
\(\frac{\hat{i}+2\hat{j}+3\hat{k}}{\sqrt{14}}\)
Check Answer
Option D
Q.No:9 JAM-2019
A unit vector perpendicular to the plane containing \(\vec{A}=\hat{i}+\hat{j}-2\hat{k}\) and \(\vec{B}=2\hat{i}-\hat{j}+\hat{k}\) is
(A)
\(\frac{1}{\sqrt{26}}(-\hat{i}+3\hat{j}-4\hat{k})\)
(B)
\(\frac{1}{\sqrt{19}}(-\hat{i}+3\hat{j}-3\hat{k})\)
(C)
\(\frac{1}{\sqrt{35}}(-\hat{i}+5\hat{j}-3\hat{k})\)
(D)
\(\frac{1}{\sqrt{35}}(-\hat{i}-5\hat{j}-3\hat{k})\)
Check Answer
Option D
Q.No:10 JAM-2019
If \(\phi(x,y,z)\) is a scalar function which satisfies the Laplace equation, then the gradient of \(\phi\) is
(A)
Solenoidal and irrotational
(B)
Solenoidal but not irrotational
(C)
Irrotational but not solenoidal
(D)
Neither solenoidal nor irrotational
Check Answer
Option A
Q.No:11 JAM-2019
The gradient of a scalar field \(S(x,y,z)\) has the following characteristic(s).
(A)
Line integral of a gradient is path-independent
(B)
Closed line integral of a gradient is zero
(C)
Gradient of S is a measure of the maximum rate of change in the field S
(D)
Gradient of S is a scalar quantity
Check Answer
Option A,B,C
Q.No:12 JAM-2020
The volume integral \(\int_V e^{-\left(\frac{r}{R}\right)^2}\vec{\nabla }\cdot \left(\frac{\hat{r}}{r^2}\right)d^3 r\), where \(V\) is the volume of a sphere of radius \(R\) centered at the origin, is equal to
(A)
\(4\pi\)
(B)
\(0\)
(C)
\(\frac{4}{3}\pi R^3\)
(D)
\(1\)
Check Answer
Option A
Q.No:13 JAM-2020
The line integral of the vector function \(u(x,y)=2y \hat{i}+x\hat{j}\) along the straight line from (0, 0) to (2, 4) is ______________
Check Answer
Ans 12
Q.No:14 JAM-2020
Consider a vector function \(\vec{u}(\vec{r})\) and two scalar functions \(\psi(\vec{r})\) and \(\Phi(\vec{r})\). The unit vector \(\hat{n}\) normal to the elementary surface \(dS\), \(dV\) is an infinitesimal volume, \(\vec{dl}\) is an infinitesimal line element, and \(\partial/\partial n\) denotes the partial derivative along \(\hat{n}\). Which of the following identities is/are correct?
(A)
\(\int_V \vec{\nabla}\cdot \vec{u}dV=\oint_S\vec{u}\cdot \hat{n} dS\), where surface \(S\) bounds the volume \(V\).
(B)
\(\int_V [\psi \nabla^2 \Phi -\Phi \nabla^2\psi] dV=\oint_S [\psi \frac{\partial \Phi}{\partial n}-\Phi\frac{\partial \psi}{\partial n}] dS\), where surface \(S\) bounds the volume \(V\).
(C)
\(\int_V [\psi \nabla^2 \Phi -\Phi \nabla^2\psi] dV=\oint_S [\psi \frac{\partial \Phi}{\partial n}+\Phi\frac{\partial \psi}{\partial n}] dS\), where surface \(S\) bounds the volume \(V\).
(D)
\(\oint_C \vec{u}\cdot \vec{dl}=\iint_S(\vec{\nabla}\times \vec{u})\cdot \hat{n} dS\),where \(C\) is the boundary of surface \(S\).
Check Answer
Option A,B,D
Q.No:15 JAM-2022
Let \((r,\theta)\) denote the polar coordinates of a particle moving in a plane. If \(\hat{r}\) and \(\hat{\theta}\) represent the corresponding unit vectors, then
(A)
\[\frac{d\hat{r}}{d\theta} = \hat{\theta}\]
(B)
\[\frac{d\hat{r}}{dr} = -\hat{\theta}\]
(C)
\[\frac{d\hat{\theta}}{d\theta} = -\hat{r}\]
(D)
\[\frac{d\hat{\theta}}{dr} = \hat{r}\]
Check Answer
Option A,C
Q.No:16 JAM-2022
Consider a unit circle \(C\) in the xy plane with center at the origin. The line integral of the vector field, \(\vec{F}(x,y,z)=-2y\hat{x}-3z\hat{y}+x\hat{z}\), taken anticlockwise over \(C\) is ______________ \(\pi\).
Check Answer
Ans 2
Q.No:17 JAM-2023
Which of the following fields has non-zero curl?
A) \(x\hat{i}+y\hat{j}+z\hat{k}\)
B) \((y+z)\hat{i}+(x+z)\hat{j}+(x+y)\hat{k}\)
C) \(y^2\hat{i}+(2xy+z^2)\hat{j}+2yz\hat{k}\)
D) \(xy\hat{i}+2yz\hat{j}+3xz\hat{k}\)
Check Answer
Option D
Q.No:18 JAM-2023
For a given vector \(\vec{F}=-y \hat{i}+z \hat{j}+x^2 \hat{k}\) , the surface integral \(\int_S (\vec{\nabla} \times \vec{F} )\cdot \hat{r}\hspace{0.5mm} dS\) over the surface \(S\) of a hemisphere of radius \(R\) with the centre of the base at the origin is

A) \(\pi R^2\)
B) \(\frac{2\pi R^2}{3}\)
C) \(-\pi R^2\)
D) \(-\frac{2\pi R^2}{3}\)
Check Answer
Option A
Q.No:19 JAM-2023
Unit vector normal to the equipotential surface of \(V(x,y,z)=4x^2+y^2+z\) at (1,2,1) is given by \((a\hat{i}+b\hat{j}+c \hat{k})\). The value of \(|b|\) is _______________________________________ (rounded off to two decimal places).
Check Answer
Ans 0.43 - 0.45
Q.No:20 JAM-2024
The divergence of a 3-dimensional vector \(\frac{\hat{r}}{r^3}\) (\(\hat{r}\) is the unit radial vector) is:
A) \(-\frac{1}{r^4}\)
B) Zero
C) \(\frac{1}{r^3}\)
D) \(-\frac{3}{r^4}\)
Check Answer
Option A
Q.No:21 JAM-2024
The value of the line integral for the vector,
\[ \vec{v} = 2\hat{x} + yz^2\hat{y} + (3y + z^2)\hat{z} \]
along the closed path \(OABO\) (as shown in the figure) is:

(Path AB is the arc of a circle of unit radius)
A) \(\frac{1}{4}(3\pi - 1)\)
B) \(3\pi - \frac{1}{4}\)
C) \(\frac{3\pi}{4} - 1\)
D) \(3\pi - 1\)
Check Answer
Option A
Q.No:22 JAM-2024
In the \(x\)-\(y\) plane, a vector is given by
\[ \vec{F}(x, y) = \frac{-y\hat{x} + x\hat{y}}{x^2 + y^2} . \]
The magnitude of the flux of \(\vec{\nabla} \times \vec{F}\), through a circular loop of radius 2, centered at the origin, is:
A) \(\pi\)
B) \(2\pi\)
C) \(4\pi\)
D) 0
Check Answer
Option B
Q.No:23 JAM-2024
Two sides of a triangle \( OAB \) are given by:
\[
\vec{OA} = \hat{x} + 2\hat{y} + \hat{z}, \quad \vec{OB} = 2\hat{x} - \hat{y} + 3\hat{z}
\]
The area of the triangle is _________________(Rounded off to one decimal place)
Check Answer
Ans 4.2-4.4
Q.No:24 JAM-2025
Consider a volume \( V \) enclosed by a closed surface \( S \) having unit
surface normal \( \hat{n} \).
For \( \vec r = x\hat{i} + y\hat{j} + z\hat{k} \), the value of the surface integral
\[
\frac{1}{9} \oint_S \vec r \cdot \hat{n}\, dS
\]
is
A) \(V\)
B) \(3V\)
C) \(\frac{V}{3}\)
D) \(\frac{V}{9}\)
Check Answer
Option C
Q.No:25 JAM-2025
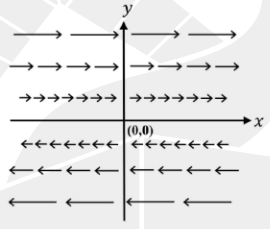
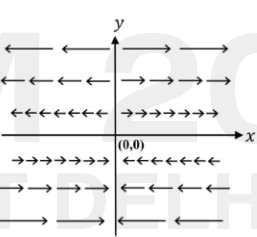
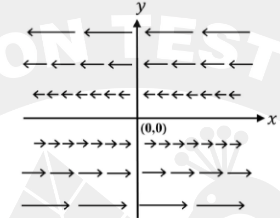
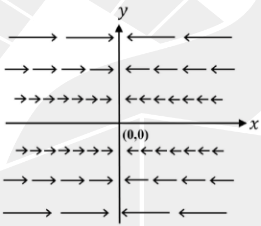
Which one of the following figures represents the vector field
\[
\vec{A} = y\,\hat{i}
\]
(\(\hat{i}\) is the unit vector along the \(x\)-direction)
Check Answer
Option A
Q.No:26 JAM-2025
Consider a vector
\[
\vec{F} = \frac{1}{\pi}\left[-\sin y \,\hat{i} + x(1-\cos y)\,\hat{j}\right].
\]
The value of the integral
\[
\oint \vec{F}\cdot d\vec{r}
\]
over the circle \(x^2 + y^2 = 1\), evaluated in the anti-clockwise direction, is
________ (in integer).

Q.No.1 Discussion :
Q1
Q.No.2 Discussion :
Sir can you check the answer. I am getting -2 instead of 2.
Answer is -2 only
Q2
Q.No.3 Discussion :
Q.No.4 Discussion :
Q.No.5 Discussion :
Volume integral of cylinder
Q.No.6 Discussion :
Volume integral of given function
Q.No.7 Discussion :
Solution
Q.No.8 Discussion :
Needs to be discussed
Q.No.9 Discussion :
Q.No.10 Discussion :
Q.No.11 Discussion :
Q.No.12 Discussion :
Q.No.13 Discussion :
Q.No.14 Discussion :
Q.No.15 Discussion :